离散时间系统模型
离散时间系统模型
离散时间系统模型是表示数字滤波器的方案。MATLAB® 科学计算环境支持若干种离散时间系统模型,这些模型将在以下章节中介绍:
- 传递函数
- 零极点增益
- 状态空间
- 部分分式展开式(残差形式)
- 二阶节 (SOS)
- 格型结构体
- 卷积矩阵
传递函数
传递函数是数字滤波器的一种基本 Z 域表示,它将滤波器表示为两个多项式的比值。它是此工具箱的主要离散时间模型。数字滤波器的差分方程的 Z 变换的传递函数模型说明如下

此处,常量 b(i) 和 a(i) 是滤波器系数,滤波器的阶数是 n 和 m 的最大值。在 MATLAB 环境中,您将这些系数存储在两个向量中(按照惯例是行向量),一个行向量用于分子,一个行向量用于分母。有关传递函数形式的详细信息,请参阅滤波器和传递函数。
零极点增益
传递函数的分解形式(又称为零极点增益形式)为
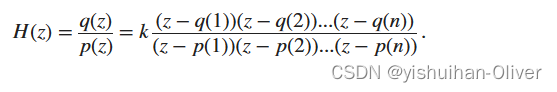
按照惯例,多项式系数存储在行向量中,多项式根存储在列向量中。因此,在零极点增益形式中,传递函数的分子和分母的零点和极点位置位于列向量中。分解传递函数增益 k 是 MATLAB 标量。
poly 和 roots 函数在多项式表示和零极点增益表示之间转换。例如,一个简单 IIR 滤波器如下
b = [2 3 4];
a = [1 3 3 1];此滤波器的零点和极点是
q = roots(b)
p = roots(a)
% Gain factor
k = b(1)/a(1)回到最初的多项式,
bb = k*poly(q)
aa = poly(p)请注意,本例中的 b 和 a 表示传递函数:
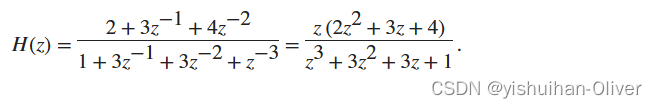
对于 b = [2 3 4],roots 函数会缺失 z 等于 0 时的零点。事实上,只要输入传递函数的极点数多于零点数(或相反),该函数都会缺失 z 等于 0 时的极点和零点。这在大多数情况下是可以接受的。然而,为了避免此问题,请在使用 roots 函数之前,直接追加零以使向量长度相同;
例如,b = [b 0]。
状态空间
将数字滤波器或差分方程组表示为一组一阶差分方程组始终是可能的。在矩阵或状态空间形式中,您可以将公式写为
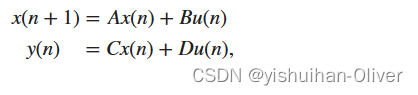 ,
,
其中 u 是输入,x 是状态向量,而 y 是输出。对于单通道系统,A 是 m×m 矩阵,其中 m 是滤波器的阶数,B 是列向量,C 是行向量,D 是标量。对于输入 u 和输出 y 成为向量、B、C 和 D 成为矩阵的多通道系统,状态空间表示法尤其方便。
状态空间表示很容易扩展到 MATLAB 环境。A、B、C 和 D 是矩形数组;MATLAB 函数将它们分别视为单个变量。
对状态空间方程进行 Z 变换并将其组合,表明状态空间形式和传递函数形式的等效性:
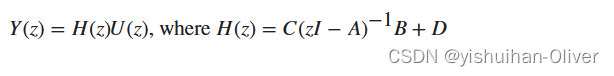
如果您不熟悉线性系统的状态空间表示,不要担心。一些滤波器设计算法在内部使用状态空间形式,但无需了解任何状态空间概念即可成功使用它们。不过,如果您的应用大量使用基于状态空间的信号处理,请了解 Control System Toolbox™ 产品,以获得全面的状态空间工具库。
部分分式展开式(残差形式)
每个传递函数还具有对应的部分分式展开(又称为残差形式),如下式所示

前提是 H(z) 没有重复的极点。此处,n 是有理传递函数 b(z)/a(z) 的分母多项式的次数。如果 r 是重极点 sr,则 H (z) 具有以下形式的项:

Signal Processing Toolbox™ 中的 residuez 函数用于将传递函数转换为部分分式展开式形式,或者反之。residuez 末尾的“z”表示 z 域或离散域。residuez 以列向量 p 形式返回极点,以列向量 r 形式返回极点对应的残差,以行向量 k 形式返回原始传递函数的任何不恰当部分。如果两个极点的差值的模小于任一极点的模的 0.1%,则 residuez 确定这两个极点相同。
部分分式展开式在信号处理中以一种求传递函数的逆 Z 变换的方法出现。例如,下式
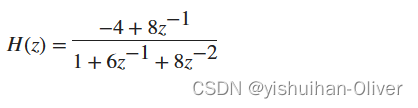
的部分分式展开式是
b = [-4 8];
a = [1 6 8];
[r,p,k] = residuez(b,a)它对应于

要想求出 H(z) 的逆 Z 变换,可以求 H(z) 的两个加数的逆 Z 变换之和,这可给出因果冲激响应:
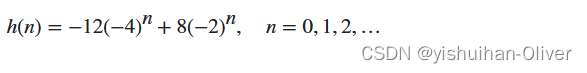
要在 MATLAB 环境中验证这一点,请键入
imp = [1 0 0 0 0];
resptf = filter(b,a,imp)
respres = filter(r(1),[1 -p(1)],imp)+...filter(r(2),[1 -p(2)],imp)二阶节 (SOS)
任何传递函数 H(z) 都有二阶节表示
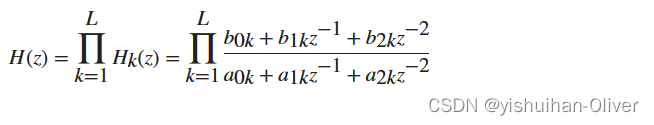
其中 L 是描述系统的二阶节的数量。MATLAB 环境将离散时间系统的二阶节形式表示为 L×6 数组 sos。sos 的每行包含一个二阶节,其中行元素是描述该二阶节的三个分子和三个分母系数。
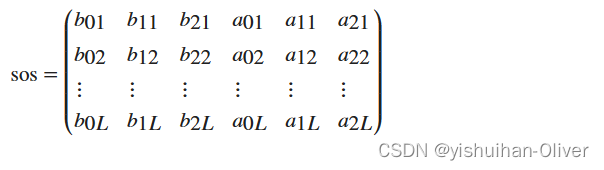
有许多方法以二阶节形式表示滤波器。通过仔细对极点和零点对组进行配对、对级联中的各节进行排序以及对各节进行乘性定标,可以在某些定点滤波器实现中降低量化噪声增益并避免溢出。Linear System Transformations 中所述的函数 zp2sos 和 ss2sos 用于执行零极点配对、节缩放和节排序。
注意
所有 Signal Processing Toolbox 二阶节变换仅适用于数字滤波器。
格型结构体
对于由多项式系数 a(n) 说明的离散的 N 阶全极点或全零滤波器,n = 1,2...,N+1,有 N 个对应的格型结构体系数 k (n),n = 1,2...,N。参数 k (n) 也称为滤波器的反射系数。给定这些反射系数,您可以实现如下所示的离散滤波器。
FIR 和 IIR 格型滤波器结构图
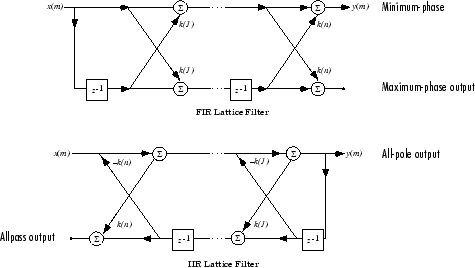
对于由多项式系数 a 和 b 说明的一般零极点 IIR 滤波器,分母 a 有格型系数 k (n),分子 b 有阶梯系数 v (n)。格型/梯形滤波器可以实现为
格型/梯形滤波器示意图
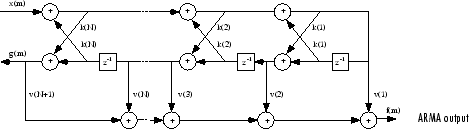
工具箱函数 tf2latc 接受多项式形式的 FIR 或 IIR 滤波器,并返回对应的反射系数。多项式形式的 FIR 滤波器的一个示例是
b = [1.0000 0.6149 0.9899 0.0000 0.0031 -0.0082];
此滤波器的格型(反射系数)表示为
k = tf2latc(b)
对于 IIR 滤波器,反射系数的幅值提供简单的稳定性检查。如果对应于一个多项式的所有反射系数的量级都小于 1,则该多项式的所有根都在单位圆内。例如,假设某 IIR 滤波器具有上述分子多项式 b 和如下的分母多项式:
a = [1 1/2 1/3];
则该滤波器的格型表示为
[k,v] = tf2latc(b,a);
对于 k 中的所有反射系数,abs(k) < 1,因此该滤波器是稳定的。
函数 latc2tf 根据滤波器的格型(反射)系数计算滤波器的多项式系数。给定反射系数向量 k,对应的多项式形式为
b = latc2tf(k);
格型或格型/梯形系数可用于使用函数 latcfilt 实现滤波器。
卷积矩阵
在信号处理中,对两个向量或矩阵求卷积等效于用一个输入操作数对另一个输入操作数进行滤波。这种关系支持将数字滤波器表示为卷积矩阵。
给定任意向量,工具箱函数 convmtx 生成一个矩阵,该矩阵与另一个向量的内积等于这两个向量的卷积。生成的矩阵表示一个数字滤波器,您可以将其应用于适当长度的任何向量;操作数的内部维度必须一致才能计算内积。
表示数字滤波器分子系数的向量 b 的卷积矩阵为
b = [1 2 3];
x = randn(3,1);
C = convmtx(b',3);求 b 与 x 的卷积的两种等效方法如下。
y1 = C*x;
y2 = conv(b,x);相关文章:

离散时间系统模型
离散时间系统模型 离散时间系统模型是表示数字滤波器的方案。MATLAB 科学计算环境支持若干种离散时间系统模型,这些模型将在以下章节中介绍: 传递函数零极点增益状态空间部分分式展开式(残差形式)二阶节 (SOS)格型结构体卷积矩…...
Nginx学习(在 Docker 中使用 Nginx)
1. 安装Nginx 使用 docker pull nginx 下载最新的 Nginx Docker 镜像。 下载完毕后,使用 docker run -d -p 80:80 --name nginx nginx,即可启动 Nginx 容器。其中,-p 80:80 表示将容器的 80 端口映射到 主机的 80 端口;--name ng…...
【Java】集合(一)单列集合List
1.集合 可以动态保存任意多个对象,并提供了一系列的操作对象的方法:add、remove、set、get等。 2.集合框架体系 分为两大类: 单列集合和双列集合 3.List接口基本介绍 List接口是Collection接口的子接口 List集合类中元素有序࿰…...

实战 | 基于卷积神经网络的蘑菇识别微信小程序
一个不知名大学生,江湖人称菜狗 original author: Jacky Li Email : 3435673055qq.com Time of completion:2023.11.13 Last edited: 2023.11.13 导读:其实没啥难的,主要是随手搞了就发出来把,太久没有水过帖子了&…...

如何选择共享wifi项目服务商,需要注意哪些?
在移动互联网时代,无线网络已经成为人们生活中不可或缺的一部分。随着5G时代的到来,共享WiFi项目成为了市场上备受关注的焦点。在众多共享WiFi公司中,如何选择共享wifi项目服务商合作,今天我们就来盘点下哪些公司可靠!…...

ubuntu20.04 MYNTEYE S 相机运行与标定记录
ubuntu20.04 MYNTEYE S 相机运行与标定记录 环境 ubuntu20.04 opencv3.3.1 硬件 mynteye S1030 OpenCV 3.4.3 安装 Jetson Nano小觅相机(MYNT EYE S)开发调试指南 mkdir -p ~/tools/opencv cd ~/tools/opencvgit clone https://github.com/opencv/opencv.git cd opencv/…...
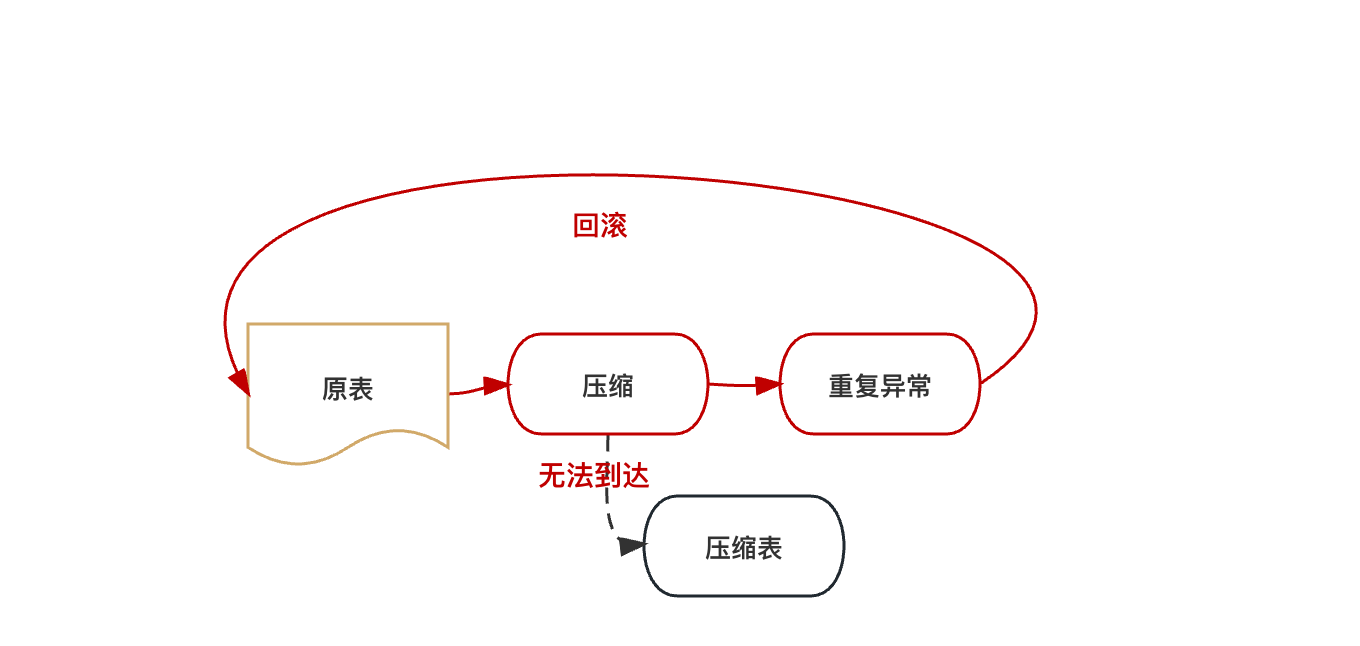
有效降低数据库存储成本方案与实践 | 京东云技术团队
背景 随着平台的不断壮大,业务的不断发展,后端系统的数据量、存储所使用的硬件成本也逐年递增。从发展的眼光看,业务与系统要想健康的发展,成本增加的问题必须重视起来。目前业界普遍认同开源节流大方向,很多企业部门…...
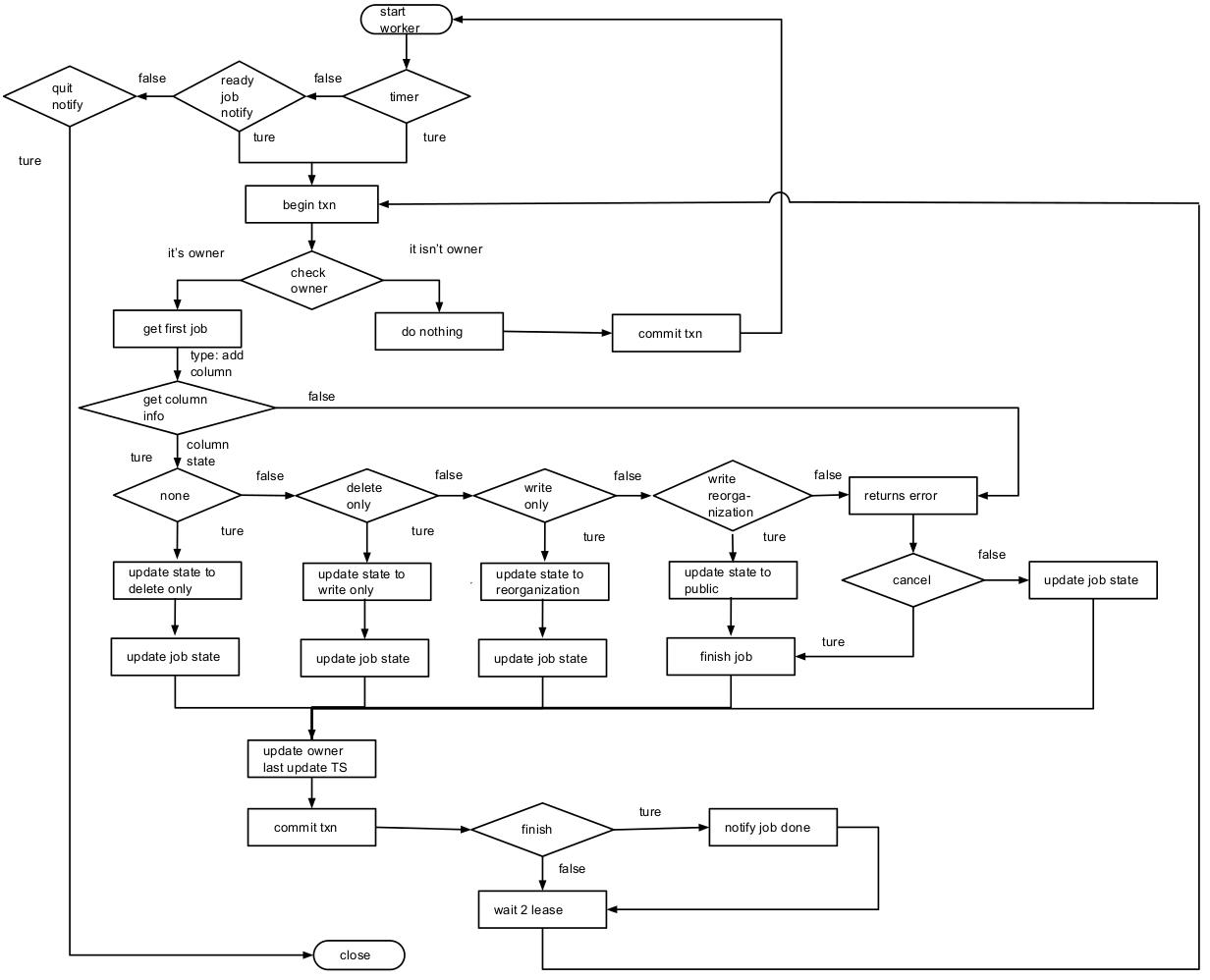
分布式数据库Schema 变更 in F1 TiDB
分布式数据库Schema 变更 in F1 & TiDB 【转载】TiDB 源码阅读系列文章(十七)DDL 源码解析 | PingCAP 上述文章主要叙述了从DDL语句发起到执行的过程,简单介绍了弄一套相同的模式来后台处理数据回填,从而提高DDL的并发度的一…...

图形库篇 | EasyX | 图像处理
图形库篇 | EasyX | 图像处理 图像类型 IMAGE表示图像,用于定义一个图像变量,与导入的图片资源一一对应。 IMAGE img;加载与绘制图像 函数功能函数加载图像void loadimage(IMAGE* pDstImg,LPCTSTR pImgFile,int nwidth = 0,int nHeight = 0,bool bResize = false)绘制图像v…...

AWTK UI 自动化测试工具发布
AWTK UI 自动化 提供了兼容 Appium 的接口,可以使用 Appium 的工具来进行 UI 自动化测试。但是使用起来有点麻烦,用的人不多,所以最终决定开发一个 AWTK 专用的 UI 自动化测试工具。相比 Appium,这个工具有下列特点: …...
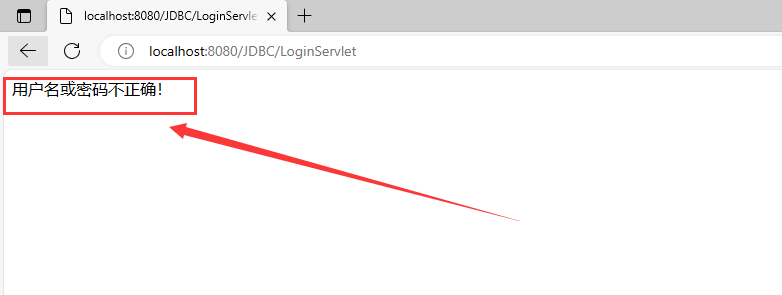
Java后端开发——JDBC入门实验
JDBC(Java Database Connectivity)是Java编程语言中用于与数据库建立连接并进行数据库操作的API(应用程序编程接口)。JDBC允许开发人员连接到数据库,执行各种操作(如插入、更新、删除和查询数据)…...

LCA
定义 最近公共祖先简称 LCA(Lowest Common Ancestor)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。 性质 如果 不为 的祖先并且 不为 的祖先,那么 分别处于 的两棵不同子树中&#…...

ts学习02-数据类型
新建index.html <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> </h…...

javaSE的发展历史以及openjdk和oracleJdk
1 JavaSE 的发展历史 1.1 Java 语言的介绍 SUN 公司在 1991 年成立了一个称为绿色计划(Green Project)的项目,由 James Gosling(高斯林)博士领导,绿色计划的目的是开发一种能够在各种消费性电子产品&…...
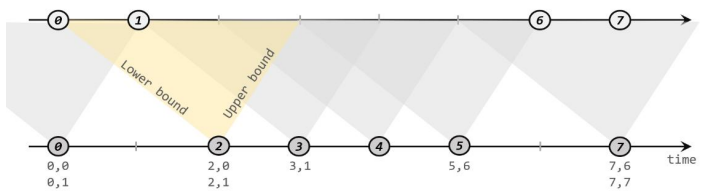
【入门Flink】- 10基于时间的双流联合(join)
统计固定时间内两条流数据的匹配情况,需要自定义来实现——可以用窗口(window)来表示。为了更方便地实现基于时间的合流操作,Flink 的 DataStrema API 提供了内置的 join 算子。 窗口联结(Window Join) 一…...

【Python Opencv】图片与视频的操作
文章目录 前言一、opencv图片1.1 读取图像1.2 显示图像1.3 写入图像1.4 示例代码 二、Opencv视频2.1 从相机捕获视频获取摄像头一帧一帧读取显示图片VideoCapture 中的get和set函数示例代码 2.2 从文件播放视频示例代码 2.3 保存视频示例代码 总结 前言 在计算机视觉和图像处理…...
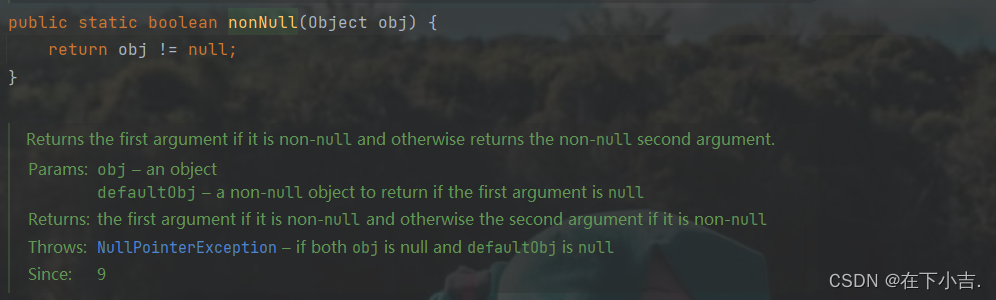
【从入门到起飞】JavaAPI—System,Runtime,Object,Objects类
🎊专栏【JavaSE】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 🎄欢迎并且感谢大家指出小吉的问题🥰 文章目录 🍔System类⭐exit()⭐currentTimeMillis()🎄用…...
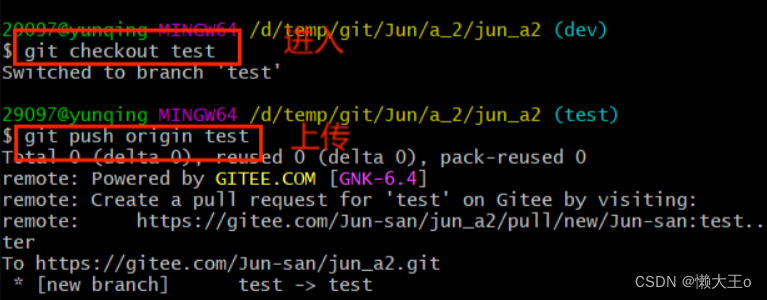
【Git】的分支和标签的讲解及实际应用场景
目录 讲解 环境讲述 分支标签的区别 分支 命令 场景应用 标签 命令 标签规范 讲解 环境讲述 当软件从开发到正式环境部署的过程中,不同环境的作用 开发环境:用于开发人员进行软件开发、测试和调试。在这个环境中,开发人员可以快速地…...
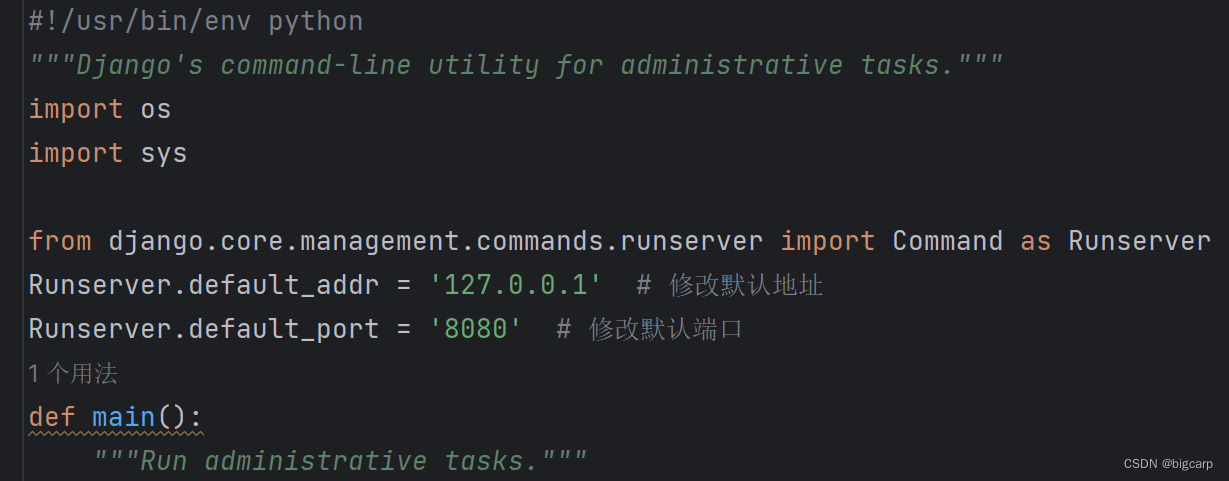
修改django开发环境runserver命令默认的端口
runserver默认8000端口 虽然python manage.py runserver 8080 可以指定端口,但不想每次runserver都添加8080这个参数 可以通过修改manage.py进行修改,只需要加三行: from django.core.management.commands.runserver import Command as Ru…...

kubeadm安装k8s高可用集群
目录 一、环境规划 二、注意事项: 三、环境准备: 1. 关闭防火墙规则,关闭selinux,关闭swap交换: 2. 修改主机名 3. 所有节点修改hosts文件: 4. 所有节点时间同步: 5. 所有节点实现Linux的资…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
