数据结构与算法(二)动态规划(Java)
目录
- 一、简介
- 1.1 什么是动态规划?
- 1.2 动态规划的两种形式
- 1)自顶向下的备忘录法(记忆化搜索法)
- 2)自底向上的动态规划
- 3)两种方法对比
- 1.3 动态规划的 3 大步骤
- 二、小试牛刀:钢条切割
- 2.1 题目描述
- 2.2 题目解析
- 1)第一步:定义数组元素的含义
- 2)第二步:找出数组元素之间的关系
- 3)第三步:找出初始值
- 2.3 最优子结构
- 2.4 代码实现
- 1)递归版本
- 2)备忘录版本
- 3)自底向上的动态规划

一、简介
1.1 什么是动态规划?
在说明动态规划前,我们先来了解一个小场景:
A: "1+1+1+1+1+1+1+1"A: "上面等式的值是多少?"
B: "(计算...)" "8!"A: "在上面等式的左边写上 '1+',此时等式的值为多少?"
B: "(立刻回答)" "9!"
A: "你这次怎么这么快就知道答案了"
B: "只要在8的基础上加1就行了"
由上面的小故事可知,动态规划 就是 通过记住历史的求解结果来节省时间 。
1.2 动态规划的两种形式
示例:斐波那契数列,又称黄金分割数列,其数值为:1、1、2、3、5、8、13、21、34,递推公式为:
F ( 0 ) = 1 , F ( 1 ) = 1 , F ( n ) = F ( n − 1 ) + F ( n − 2 ) , n > 2 , n ∈ N ∗ F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2),n>2,n∈N^{*} F(0)=1,F(1)=1,F(n)=F(n−1)+F(n−2),n>2,n∈N∗
这个算法用递归来实现非常简单,代码如下:
public int fib(int n) {if (n < 2) {return 1;}return fib(n - 1) + fib(n - 2);
}
先来分析一下递归算法的执行流程,假如输入 6,那么执行的递归树如下:
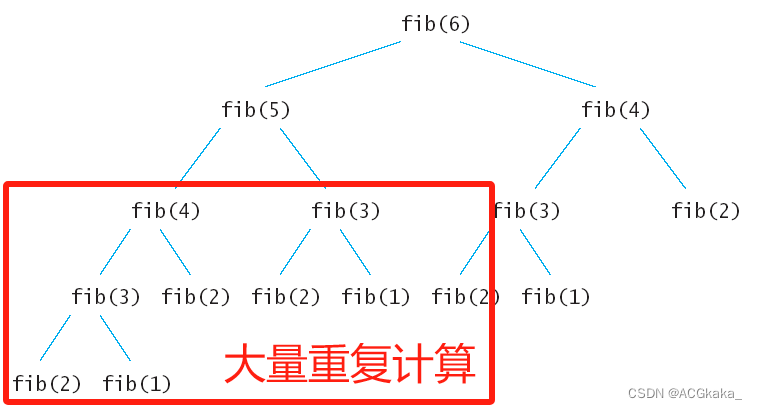
我们可以发现:
- 上面的递归树中,每一个结点都会执行一次;
- 很多结点被重复执行。
为了避免这种情况,我们可以把执行过的结点值保存下来,后面用到直接查表,这样可以节省大量时间。
下面看下保存历史记录的两种形式:自顶向下的备忘录法、自底向上的动态规划。
1)自顶向下的备忘录法(记忆化搜索法)
备忘录法,也叫记忆化搜索法,是比较好理解的:
- 创建了一个 n+1 大小的数组来保存求出斐波那契数列中的每一个值;
- 在递归的时候,如果发现之前已经算过了就不再计算;
- 如果之前没有计算,则计算后放入历史记录中。
public static void main(String[] args) {int n = 6;// 声明数组,用于记录历史,初始化为-1int[] his = new int[n + 1];Arrays.fill(his, -1);System.out.println(fib(n, his));
}public static int fib(int n, int[] his) {if (n < 2) {return 1;}// 读取历史if (his[n] != -1) {return his[n];}int result = fib(n - 1, his) + fib(n - 2, his);// 记录历史his[n] = result;return result;
}
2)自底向上的动态规划
备忘录法还是利用了递归,不管怎样,当计算 fib(6) 的时候还是要去先计算出 fib(1) ~ fib(5),那么为何不先计算出 f(1) ~ f(5) 呢?这就是动态规划的核心:先计算子问题,再由子问题计算父问题。
public static int fib(int n) {int[] arr = new int[n + 1];arr[0] = 1;arr[1] = 1;for (int i = 2; i <= n; i++) {arr[i] = arr[i - 2] + arr[i - 1];}return arr[n];
}
自底向上的动态规划方法也是利用数组保存了计算的值,为后面的计算使用。
内存空间优化:
我们观察上面的代码会发现:参与循环的只有 fib(i)、fib(i-1)、fib(i-2) 项,因此该方法的空间可以进一步的压缩如下:
public static int fib(int n) {int num_i = 0;int num_i_1 = 1;int num_i_2 = 1;for (int i = 2; i <= n; i++) {num_i = num_i_2 + num_i_1;num_i_2 = num_i_1;num_i_1 = num_i;}return num_i;
}
3)两种方法对比
- 一般来说,由于备忘录的动态规划形式使用了递归,递归的时候会产生额外的开销,所以不推荐。
- 相比之下,使用自底向上的动态规划方法要好些,也更容易理解。
1.3 动态规划的 3 大步骤
动态规划,无非就是利用 历史记录,来避免我们的重复计算。这些历史记录的存储,一般使用 一维数组 或 二维数组 来保存。
第一步:定义数组元素的含义
- 上面说了,我们用一个数组来保存历史数据,假设用一维数组
dp[]来保存。这个时候有一个非常重要的点:如何规定数组元素的含义? 即dp[i]代表什么意思?
第二步:找出数组元素之间的关系
- 动态规划类似于我们高中学习的
数学归纳法。当我们要计算d[i]时,可以利用 dp[i-1]、dp[i-2] … dp[1] 来推导证明。
第三步:找出初始值
- 学过
数学归纳法的都知道,虽然知道了数组元素之间的关系式后,可以通过 dp[i-1] 和 dp[i-2] 来计算 dp[i],但是我们首先至少要知道dp[0]和dp[1]才能推导后面的值。dp[0] 和 dp[1] 就是所谓的初始值。
二、小试牛刀:钢条切割
2.1 题目描述
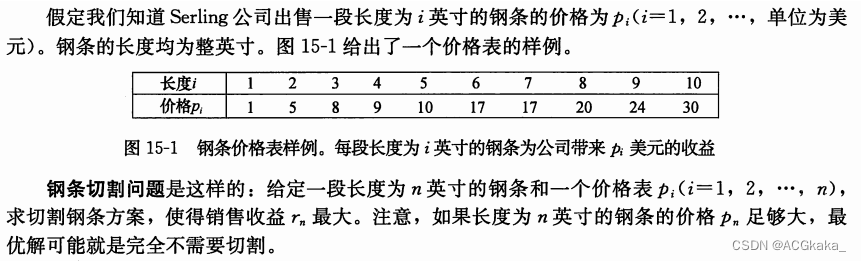
2.2 题目解析
1)第一步:定义数组元素的含义
由题目可知:
p[]是价格数组,长度为i英寸的钢条价格为p[i];r[]是最大收益数组,长度为i英寸的钢条可以获得的最大收益为r[i];- 钢条的价格不确定,可能切割的收益更高,也可能不切割的收益更高。
通过解析可知,数组元素含义: 长度为 i 英寸的钢条可以获得的最大收益为 r[i]。
注意: 这里的 收益是指价格的总和,比如:2 英寸的钢条切割后收益为:1+1=2,相比之下不切割的 5 收益更高。
2)第二步:找出数组元素之间的关系
假如我们要对长度为 4 英寸的钢条进行切割,所有切割方案如下:

由图可见,我们将 r[4] 的计算转换成了 r[1]~ r[3] 的计算。
r 4 = m a x ( r 1 + r 3 , r 1 + r 1 + r 2 , r 2 + r 2 , p 4 ) ; r_{4}=max(r_{1}+r_{3},r_{1}+r_{1}+r_{2},r_{2}+r_{2},p_{4}); r4=max(r1+r3,r1+r1+r2,r2+r2,p4);
以此类推,可以继续转换 r[3]:

由图可见,我们继续将 r[3] 的计算转换成了 r[1]~r[2] 的计算。
r 3 = m a x ( r 1 + r 2 , r 1 + r 1 + r 1 , p 3 ) r_{3}=max(r_{1}+r_{2},r_{1}+r_{1}+r_{1},p_{3}) r3=max(r1+r2,r1+r1+r1,p3)
以此类推,可以继续转换 r[2]:
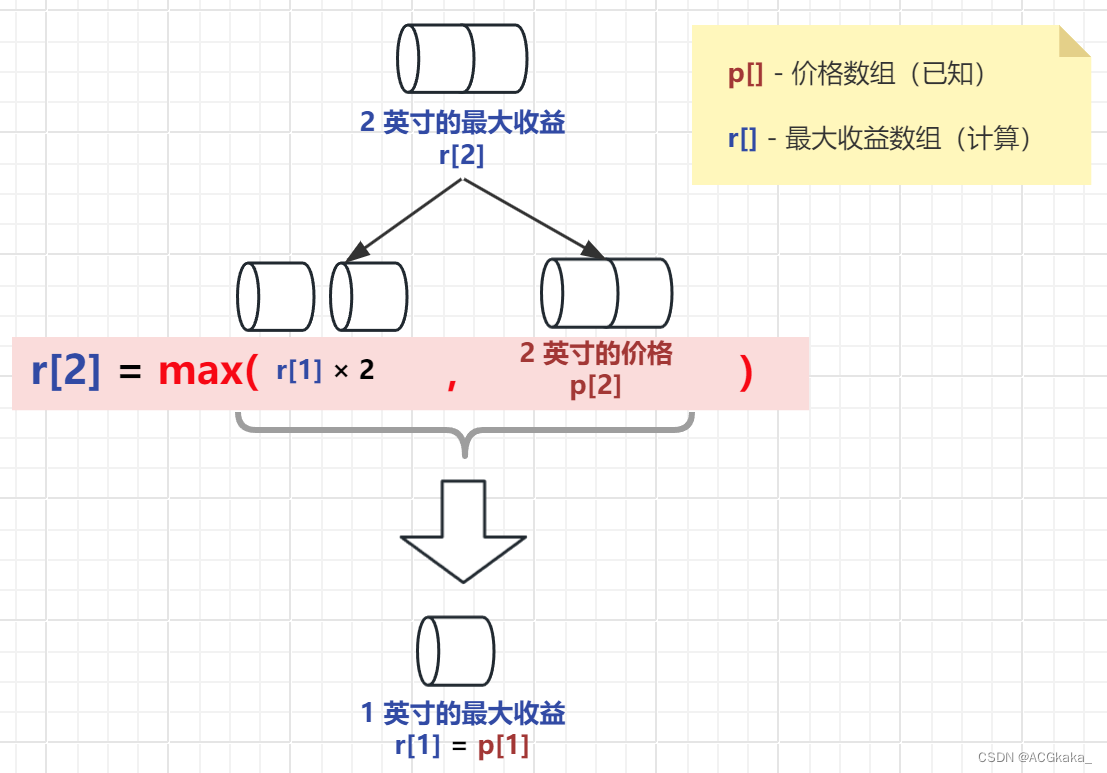
由于 1 英寸的钢条无法切割,所以 r[1]=p[1]。
r 2 = m a x ( r 1 + r 1 , p 2 ) r_{2}=max(r_{1}+r_{1},p_{2}) r2=max(r1+r1,p2)
由于 r[2] 中包含了 r[1] + r[1],那么 r[3] 中的:
m a x ( r 1 + r 2 , r 1 + r 1 + r 1 ) = m a x ( r 1 + r 2 ) max(r_{1}+r_{2},r_{1}+r_{1}+r_{1})=max(r_{1}+r_{2}) max(r1+r2,r1+r1+r1)=max(r1+r2)
由于 r[3] 中包含了 r[1] + r[2],那么 r[4] 中的:
m a x ( r 1 + r 3 , r 1 + r 1 + r 2 ) = m a x ( r 1 + r 3 ) max(r_{1}+r_{3},r_{1}+r_{1}+r_{2})=max(r_{1}+r_{3}) max(r1+r3,r1+r1+r2)=max(r1+r3)
所以整理 r[1]、r[2]、r[3]、r[4] 为:
r 1 = p 1 r_{1}=p_{1} r1=p1
r 2 = m a x ( r 1 + r 1 , p 2 ) r_{2}=max(r_{1}+r_{1},p_{2}) r2=max(r1+r1,p2)
r 3 = m a x ( r 1 + r 2 , p 3 ) r_{3}=max(r_{1}+r_{2},p_{3}) r3=max(r1+r2,p3)
r 4 = m a x ( r 1 + r 3 , r 2 + r 2 , p 4 ) r_{4}=max(r_{1}+r_{3},r_{2}+r_{2},p_{4}) r4=max(r1+r3,r2+r2,p4)
根据公式进行递推, r[n] 为:
r n = m a x ( r 1 + r n − 1 , r 2 + r n − 2 , . . . , r n / 2 + r n − n / 2 , p n ) r_{n}=max(r_{1}+r_{n-1},r_{2}+r_{n-2},...,r_{n/2}+r_{n-n/2},p_{n}) rn=max(r1+rn−1,r2+rn−2,...,rn/2+rn−n/2,pn)
3)第三步:找出初始值
其实初始值我们在第二步已经找出来了:
r[1]=p[1]=1r[2]=max(r[1]+r[1],p[2])=5
2.3 最优子结构
通过该题我们注意到,为了求规模为n的原问题,我们 先求解形式完全一样,但规模更小的子问题。当完成首次 切割后,我们 将两段钢条看成两个独立的钢条切割问题实例。我们 通过组合两个相关子问题的最优解,并在所有可能的两段切割方案中选取组合收益最大者,构成原问题的最优解。
我们称 钢条切割问题 满足 最优子结构 性质:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解。
2.4 代码实现
1)递归版本
递归很好理解,思路和回溯法是一样的,遍历所有解空间。但这里和上面斐波那契数列的不同之处在于:这里在每一层上都进行了一次最优解的选择,q=Math.max(q, p[i]+cut(n-i)); 这段代码就是选择最优解。
final static int[] p = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};public static int cut(int n) {if (n == 0) {return 0;}int max = Integer.MIN_VALUE;for (int i = 1; i <= n; i++) {max = Math.max(max, p[i - 1] + cut(n - i));}return max;
}
2)备忘录版本
备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。钢条切割问题的经典之处在于自底向上的动态规划问题的处理,理解了这个也就理解了动态规划的精髓。
public static int cutByHis(int n) {int[] p = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};int[] r = new int[n + 1];for (int i = 0; i <= n; i++) {r[i] = -1;}return cut(p, n, r);
}public static int cut(int[] p, int n, int[] r) {int q = -1;if (r[n] >= 0)return r[n];if (n == 0)q = 0;else {for (int i = 1; i <= n; i++)q = Math.max(q, cut(p, n - i, r) + p[i - 1]);}r[n] = q;return q;
}
3)自底向上的动态规划
自底向上的动态规划问题中最重要的是要理解在子循环遍历中的 i 变量,相当于上面两个方法中的 n 变量,i-j 主要用于获取历史计算过的问题值。
final static int[] p = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};public static int cutByDP(int n) {int[] r = new int[n + 1];for (int i = 1; i <= n; i++) {int q = -1;for (int j = 1; j <= i; j++)q = Math.max(q, p[j - 1] + r[i - j]);r[i] = q;}return r[n];
}
整理完毕,完结撒花~ 🌻
参考地址:
1.算法-动态规划 Dynamic Programming–从菜鸟到老鸟,https://blog.csdn.net/u013309870/article/details/75193592
2.告别动态规划,连刷40道动规算法题,我总结了动规的套路,https://blog.csdn.net/hollis_chuang/article/details/103045322
相关文章:

数据结构与算法(二)动态规划(Java)
目录 一、简介1.1 什么是动态规划?1.2 动态规划的两种形式1)自顶向下的备忘录法(记忆化搜索法)2)自底向上的动态规划3)两种方法对比 1.3 动态规划的 3 大步骤 二、小试牛刀:钢条切割2.1 题目描述…...

颜值实力“C位出道”:起亚EV6综合实力究竟怎么样?
作为起亚电动化转型的标杆之作,起亚EV6已在全球赢得广泛赞誉,连续斩获“2022欧洲年度汽车”及“2023北美年度汽车”等多项国际大奖,其GT版本更是荣获“2023年度世界性能车”,这些荣誉不仅标志着其设计和技术的国际认可,…...

继承和多态_Java零基础手把手保姆级教程(超详细)
文章目录 Java零基础手把手保姆级教程_继承和多态(超详细)1. 继承1.1 继承的实现(掌握)1.2 继承的好处和弊端(理解) 2. 继承中的成员访问特点2.1 继承中变量的访问特点(掌握)2.2 sup…...

AI:85-基于深度学习的自然场景生成与渲染
🚀 本文选自专栏:人工智能领域200例教程专栏 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的代码,详细讲解供大家学习,希望可以帮到大家。欢迎订阅支持,正在不断更新中,…...

Windows电脑训练 RT-DETR 改进算法 (Ultralytics) 教程,改进RTDETR算法(包括使用训练、验证、推理教程)
手把手从零开始训练 RT-DETR 改进项目 (Ultralytics版本) 教程,改进RTDETR算法 本文以Windows服务器为例:从零开始使用Windows训练 RT-DETR 算法项目 《芒果剑指 RT-DETR 目标检测算法 改进》 适用于芒果专栏改进RT-DETR算法 文章目录 百度 RT-DETR 算法介绍改进网络代码汇…...
flask框架报错解决方法
1、报错 jinja2.exceptions.TemplateNotFound 解决方法:报错jinja2.exceptions.TemplateNotFound,template没找到,由于我之前直接将.html文件和.py文件直接放在同一目录下,经了解,需要新增一个 templates目录ÿ…...
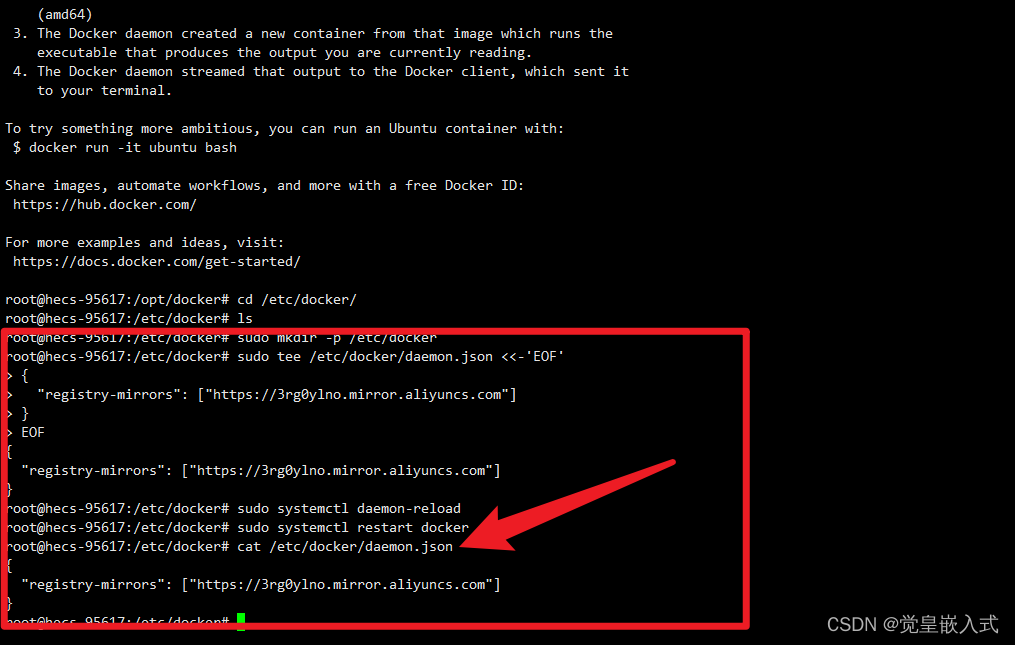
Ubuntu18.04 安装docker教程
Ubuntu18.04 安装docker教程 1、前言 Docker Engine-Community 支持以下的 Ubuntu 版本: Xenial 16.04 (LTS)Bionic 18.04 (LTS)Cosmic 18.10Disco 19.04 Docker Engine-Community 支持以下CPU架构: x86_64(或 amd64)armhfarm…...

深入理解Git
目录 一、Git 的基本构造 1.1 关键对象类型 1.2 存储机制 二、Git 的内部工作 2.1 哈希和数据完整性 2.2 引用和可达性 2.3 分支和合并 2.4 垃圾回收 三、Git 高级特性 3.1 垃圾回收 3.2 钩子(Hooks) 3.3 子模块 四、常用命令 五、最佳实践…...
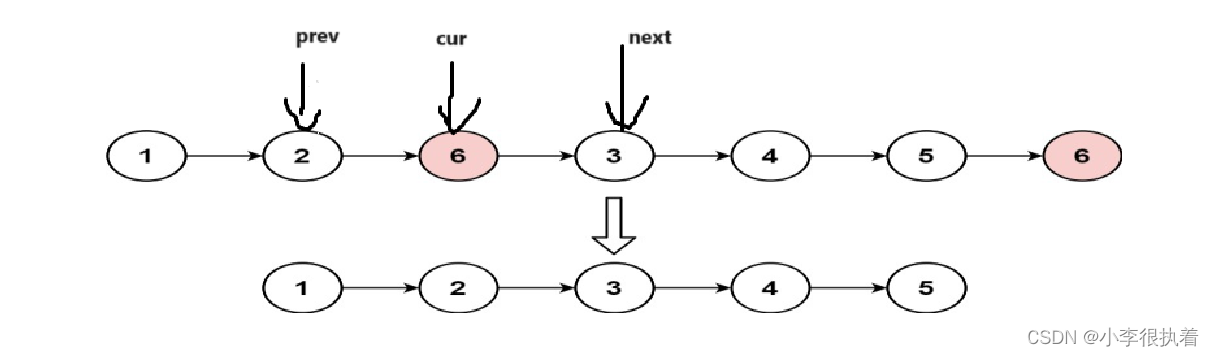
Leetcode_203.移除链表元素—C语言
目录 ❣️1.题目❣️ ❣️2.解答❣️ 💞方法一:暴力法 💞方法二: 尾插法 💞方法三:哨兵位法 ❣️1.题目❣️ 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.va…...
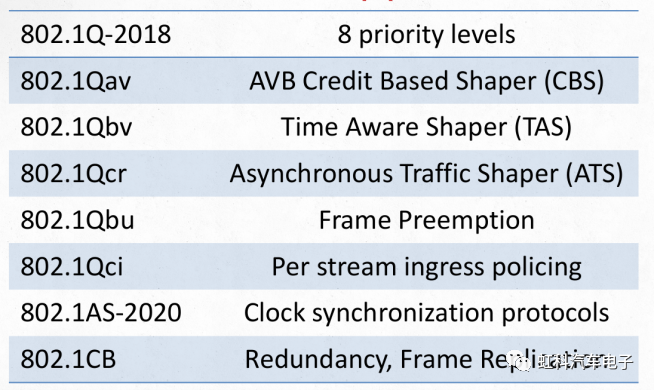
虹科方案 | 汽车电子电气架构设计仿真解决方案
来源:虹科汽车电子 虹科方案 | 汽车电子电气架构设计仿真解决方案 导读 本文将介绍面向服务(SOA)的汽车TSN网络架构,并探讨RTaW-Pegase仿真与设计软件在TSN网络设计中的应用。通过RTaW将设计问题分解,我们可以更好地理…...

Java6种单例模式写法
单例模式 某个类任何情况下只有一个实例,并提供一个全局访问点来获取该实例。Java6种单例模式:2种懒汉式,2种饿汉式 ,静态内部类 ,枚举类懒汉式 synchronized延迟加载 public class Singleton {private static Sing…...
Direct3D拾取
假设在屏幕上单击,击中的位置为点s(x,y)。由图可以看出,用户选中了茶壶。但是仅给出点s,应用程序还无法立即判断出茶壶是否被选中。所以针对这类问题,我们需要采用一项称为“拾 取(Picking)”的技术。 茶壶和屏幕点s之间的一种联…...

大洋钻探系列之二IODP 342航次是干什么的?(上)
本文简单介绍一下大洋钻探IODP 342航次,从中,我们一窥大洋钻探航次的风采。 IODP342的航次报告在网络上可以下载,英文名字叫《Integrated Ocean Drilling ProgramExpedition 342 Preliminary Report》,航次研究的主要内容是纽芬兰…...
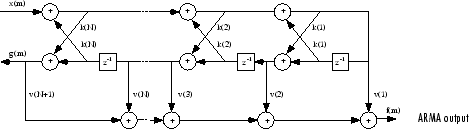
离散时间系统模型
离散时间系统模型 离散时间系统模型是表示数字滤波器的方案。MATLAB 科学计算环境支持若干种离散时间系统模型,这些模型将在以下章节中介绍: 传递函数零极点增益状态空间部分分式展开式(残差形式)二阶节 (SOS)格型结构体卷积矩…...
Nginx学习(在 Docker 中使用 Nginx)
1. 安装Nginx 使用 docker pull nginx 下载最新的 Nginx Docker 镜像。 下载完毕后,使用 docker run -d -p 80:80 --name nginx nginx,即可启动 Nginx 容器。其中,-p 80:80 表示将容器的 80 端口映射到 主机的 80 端口;--name ng…...
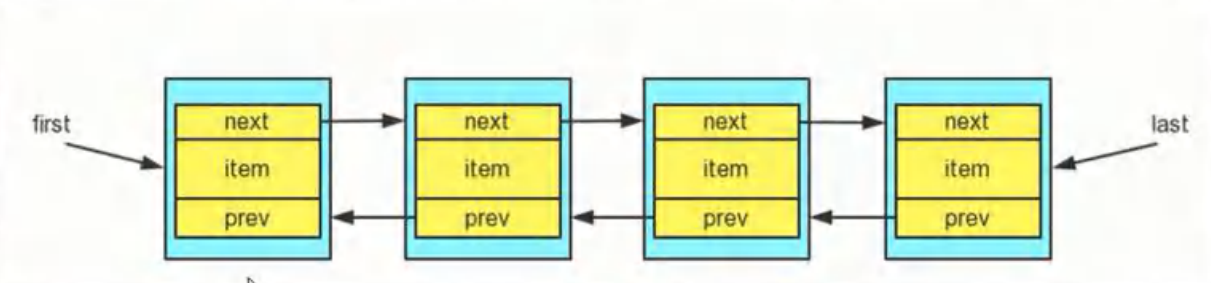
【Java】集合(一)单列集合List
1.集合 可以动态保存任意多个对象,并提供了一系列的操作对象的方法:add、remove、set、get等。 2.集合框架体系 分为两大类: 单列集合和双列集合 3.List接口基本介绍 List接口是Collection接口的子接口 List集合类中元素有序࿰…...

实战 | 基于卷积神经网络的蘑菇识别微信小程序
一个不知名大学生,江湖人称菜狗 original author: Jacky Li Email : 3435673055qq.com Time of completion:2023.11.13 Last edited: 2023.11.13 导读:其实没啥难的,主要是随手搞了就发出来把,太久没有水过帖子了&…...

如何选择共享wifi项目服务商,需要注意哪些?
在移动互联网时代,无线网络已经成为人们生活中不可或缺的一部分。随着5G时代的到来,共享WiFi项目成为了市场上备受关注的焦点。在众多共享WiFi公司中,如何选择共享wifi项目服务商合作,今天我们就来盘点下哪些公司可靠!…...

ubuntu20.04 MYNTEYE S 相机运行与标定记录
ubuntu20.04 MYNTEYE S 相机运行与标定记录 环境 ubuntu20.04 opencv3.3.1 硬件 mynteye S1030 OpenCV 3.4.3 安装 Jetson Nano小觅相机(MYNT EYE S)开发调试指南 mkdir -p ~/tools/opencv cd ~/tools/opencvgit clone https://github.com/opencv/opencv.git cd opencv/…...
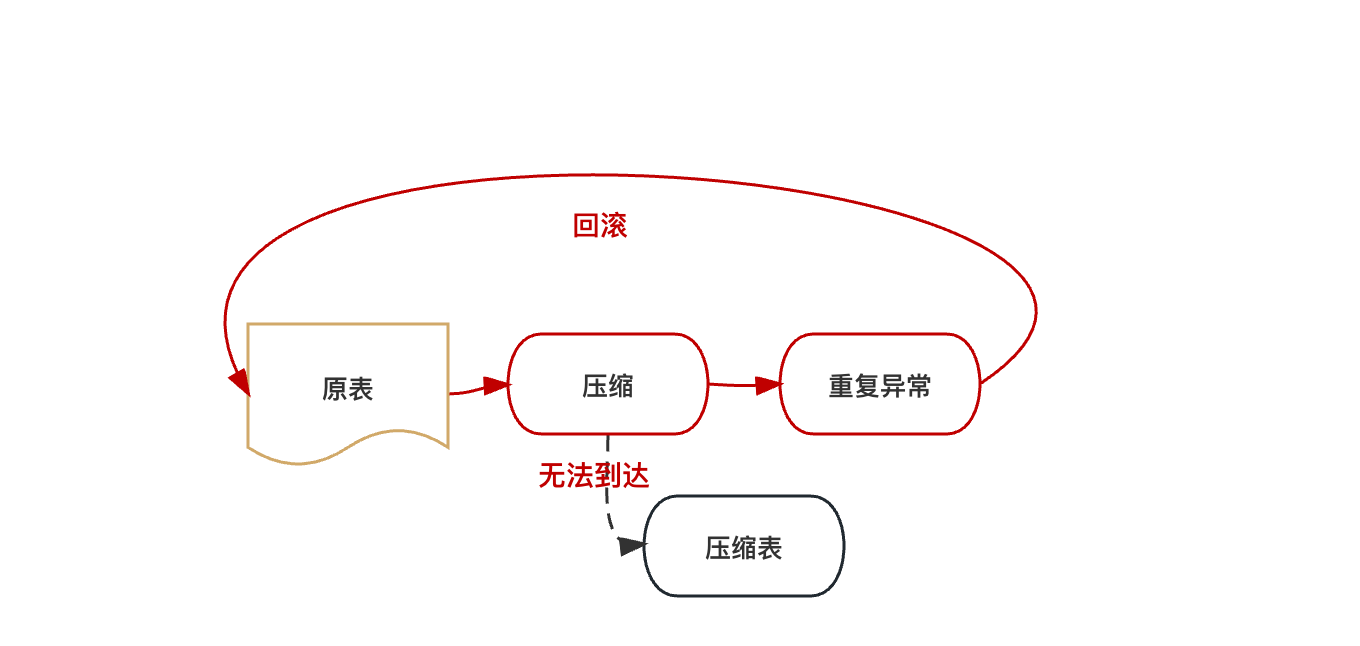
有效降低数据库存储成本方案与实践 | 京东云技术团队
背景 随着平台的不断壮大,业务的不断发展,后端系统的数据量、存储所使用的硬件成本也逐年递增。从发展的眼光看,业务与系统要想健康的发展,成本增加的问题必须重视起来。目前业界普遍认同开源节流大方向,很多企业部门…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
