【人工智能Ⅰ】6-机器学习之分类
【人工智能Ⅰ】6-机器学习之分类
6-1 机器学习在人工智能中的地位
学习能力是智能的本质
人工智能 => 机器学习 => 深度学习
什么是机器学习?
baidu:多领域交叉学科(做什么)
wiki:the study of algorithms and mathematical models(怎么做)
人工智能的核心是使计算机具有智能的根本途径
大数据建模分析的理论和方法
依赖的理论和方法:统计学、机器学习、数据挖掘、深度学习
统计学:人工学习特征,人工学习规律
机器学习:人工学习特征,自动学习规律
深度学习:自动学习特征,自动学习规律
实现基础:数据库、数据仓库、分布式存储、并行计算、流式计算、GPU加速…
机器学习历史
神经网络发展3起2落
6-2 机器学习的一般过程
历史数据:训练模型
新数据:输入模型
结果:由模型预测
即,自动学习数据规律,解决分类/回归/聚类等问题
机器学习的实质:寻找函数
6-3 机器学习的基本流程
本质:通过构建数学模型,从数据中学习特征和规律,收获有用的知识
- 特征:决定数据对象所蕴含的知识的关键属性
- 规律:将特征表达为目标知识的一种模式,及其参数
- 学习:从样本数据集计算得到规律的过程
6-4 学习方法分类
根据反馈的不同,学习技术分为:
- 监督学习(学习有标签数据)(解决分类、回归)
- 非监督学习(学习无标签数据)(解决聚类)
- 半监督学习(学习有标签和无标签数据)(海量数据分类)
- 强化学习(学习无标签但有反馈的数据)(策略推理)
半监督学习案例:图片分类
step1:用有标签图片训练分类器
step2:对无标签的数据进行分类,按照信任度从大到小排序
step3:将信任度最高的图片自动加入标识项
step4:重新训练分类器,重复step2—step4
6-5 完整的及其学习过程实施
1:数据预处理(数据清洗、数据集成、数据采样)
数据完整性、一致性、合法性等
数据采样均衡:(例如二分类问题的正负样本悬殊)
- 过采样:随机复制少数类
- 欠采样:随机消除占多数类的样本
数据集拆分:
- 训练数据集(train):构建机器学习模型
- 验证数据集(validation):辅助构建模型,评估模型并提供无偏估计,进而调整模型参数
- 测试数据集(test):评估训练好的最终模型的性能
2:特征工程(特征编码、特征选择、特征降维、规范化)
特征降维:减小特征矩阵,降低计算量和训练时间
规范化:通过归一化等进行规范
3:数据建模(回归问题、分类问题、聚类问题、其他问题)
分类:决策树、贝叶斯、SVM、逻辑回归、集成学习
回归:线性回归、广义线性回归、岭回归、Lasso回归
聚类:K-means、高斯混合聚类、密度聚类、层次聚类
其他:隐马尔可夫模型、LDA主题模型、条件随机场、神经网络、深度学习
4:结果评估(拟合度量、准确率、召回率、F1值、PR曲线等)
- 欠拟合:学习太少,划分太粗糙
- 过拟合:学习太多,划分太细致
5:总结
有监督学习(有x有y,y是标签):分类、回归
无监督学习(有x无y,只有数据没有标签):聚类、降维
6-6 贝叶斯分类方法
条件概率
P ( A ∣ B ) = P ( A B ) / P ( B ) P(A|B)=P(AB)/P(B) P(A∣B)=P(AB)/P(B)
乘法定理
P ( A B C ) = P ( A ) ∗ P ( B ∣ A ) ∗ P ( C ∣ A B ) P(ABC)=P(A)*P(B|A)*P(C|AB) P(ABC)=P(A)∗P(B∣A)∗P(C∣AB)
全概率公式
P ( A ) = ∑ i = 1 n P ( B ) ∗ P ( A ∣ B i ) P(A)=∑_{i=1}^{n}P(B)*P(A|B_i) P(A)=i=1∑nP(B)∗P(A∣Bi)
分解为若干个简单事件的概率计算问题,利用可加性求出最终的概率结果
贝叶斯公式
P ( B i ∣ A ) = P ( A ∣ B i ) ∗ P ( B i ) / ( ∑ j = 1 n P ( A ∣ B j ) ∗ P ( B j ) ) P(B_i|A)=P(A|B_i)*P(B_i)/(∑_{j=1}^nP(A|B_j)*P(B_j)) P(Bi∣A)=P(A∣Bi)∗P(Bi)/(j=1∑nP(A∣Bj)∗P(Bj))
已知A事件确已发生,求原因B_j所导致的概率(从结果分析原因)
贝叶斯分类
P ( H ∣ X ) = P ( X ∣ H ) ∗ P ( H ) / P ( X ) P(H|X)=P(X|H)*P(H)/P(X) P(H∣X)=P(X∣H)∗P(H)/P(X)
P(H):先验概率
P(H|X):后验概率(某个特定条件下具体事物发生的概率)
6-7 朴素贝叶斯分类
工作过程
1:每个数据样本用1个n维特征向量X={x1,…,xn}表示,分别描述对n个属性A1~An样本的n个度量
2:假设有m个类C1~Cm,给定1个未知数据样本X,分类器将预测X属于具有最高后验概率的类
3:根据贝叶斯定理计算,其中P(X)对于所有类为常数,因此只需要计算分子;如果先验概率位置,则假设各类是等概率的
4:给定具有许多属性的样本数据集,为降低计算P(X|Ci)的开销,可做类条件独立的朴素假定,即属性值相互条件独立
P ( A B ) = P ( A ) ∗ P ( B ) P(AB)=P(A)*P(B) P(AB)=P(A)∗P(B)
5:对未知样本X分类,对每个类Ci,计算P(X|Ci)*P(Ci)
优点
- 可运用于大量数据库,不亚于决策树、神经网络分类算法
- 方法简单,分类准确率高,速度快,所需估计的参数少,对缺失数据不敏感
缺点
- 需要知道先验概率
- 相互独立实际上难以满足
相关文章:

【人工智能Ⅰ】6-机器学习之分类
【人工智能Ⅰ】6-机器学习之分类 6-1 机器学习在人工智能中的地位 学习能力是智能的本质 人工智能 > 机器学习 > 深度学习 什么是机器学习? baidu:多领域交叉学科(做什么) wiki:the study of algorithms and…...

本地部署_语音识别工具_Whisper
1 简介 Whisper 是 OpenAI 的语音识别系统(几乎是最先进),它是免费的开源模型,可供本地部署。 2 docker https://hub.docker.com/r/onerahmet/openai-whisper-asr-webservice 3 github https://github.com/ahmetoner/whisper…...

秋招求职经验分享
0.个人简介 2023年10月底,最终拿到了海康威视、汇川技术等十余家公司的Offer,最终签了自己心仪的Offer,秋招对我来说算是正式结束了,写个博客纪念一下,顺便分享以下秋招的经验,为后来人求职提供一些参考。…...
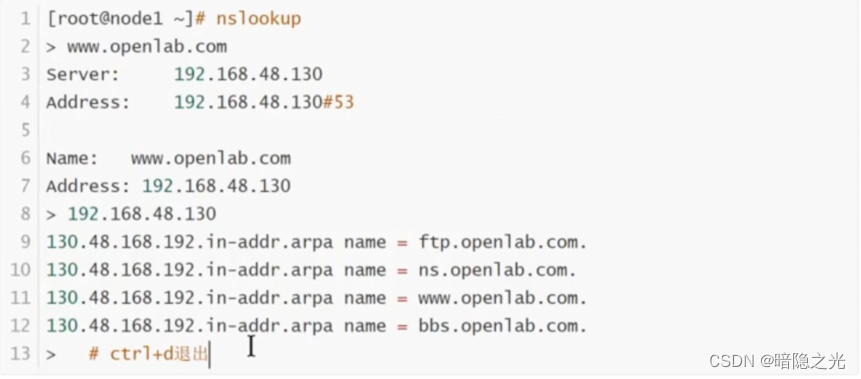
DNS域名解析
目录 1.概述 1.1产生原因 1.2作用 1.3连接方式 1.4因特网的域名结构 1.4.1拓扑 1.4.2分类 1.4.3域名服务器类型划分 2. DNS域名解析过程 2.1分类 2.2解析图 2.2.2过程分析 3.搭建DNS域名解析服务器 3.1.概述 3.2安装软件 3.3bind服务中三个关键文件 3.4主配置…...

Flink SQL --命令行的使用(02)
1、窗口函数: 1、创建表: -- 创建kafka 表 CREATE TABLE bid (bidtime TIMESTAMP(3),price DECIMAL(10, 2) ,item STRING,WATERMARK FOR bidtime AS bidtime ) WITH (connector kafka,topic bid, -- 数据的topicproperties.bootstrap.servers m…...
)
【nlp】1.3 文本数据分析(标签数量分布、句子长度分布、词频统计与关键词词云)
文本数据分析 1 文本数据分析介绍2 数据集说明3 获取标签数量分布4 获取句子长度分布5 获取正负样本长度散点分布6 获取不同词汇总数统计7 获取训练集高频形容词词云8 获取验证集形容词词云1 文本数据分析介绍 文本数据分析的作用: 文本数据分析能够有效帮助我们理解数据语料…...
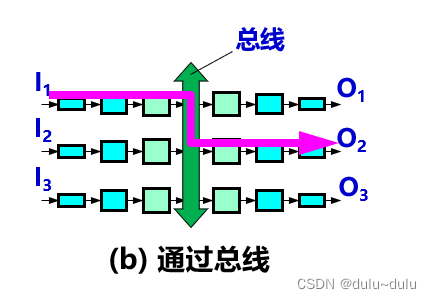
路由器的结构以及工作原理
目录 路由器的结构 交换结构三种常用的交换方式 1.通过存储器 2.通过总线 3.通过纵横交换结构(crossbar switch fabric) 路由器的结构 路由器结构可划分为两大部分:路由选择部分,分组转发部分 路由选择部分也叫做控制部分&…...
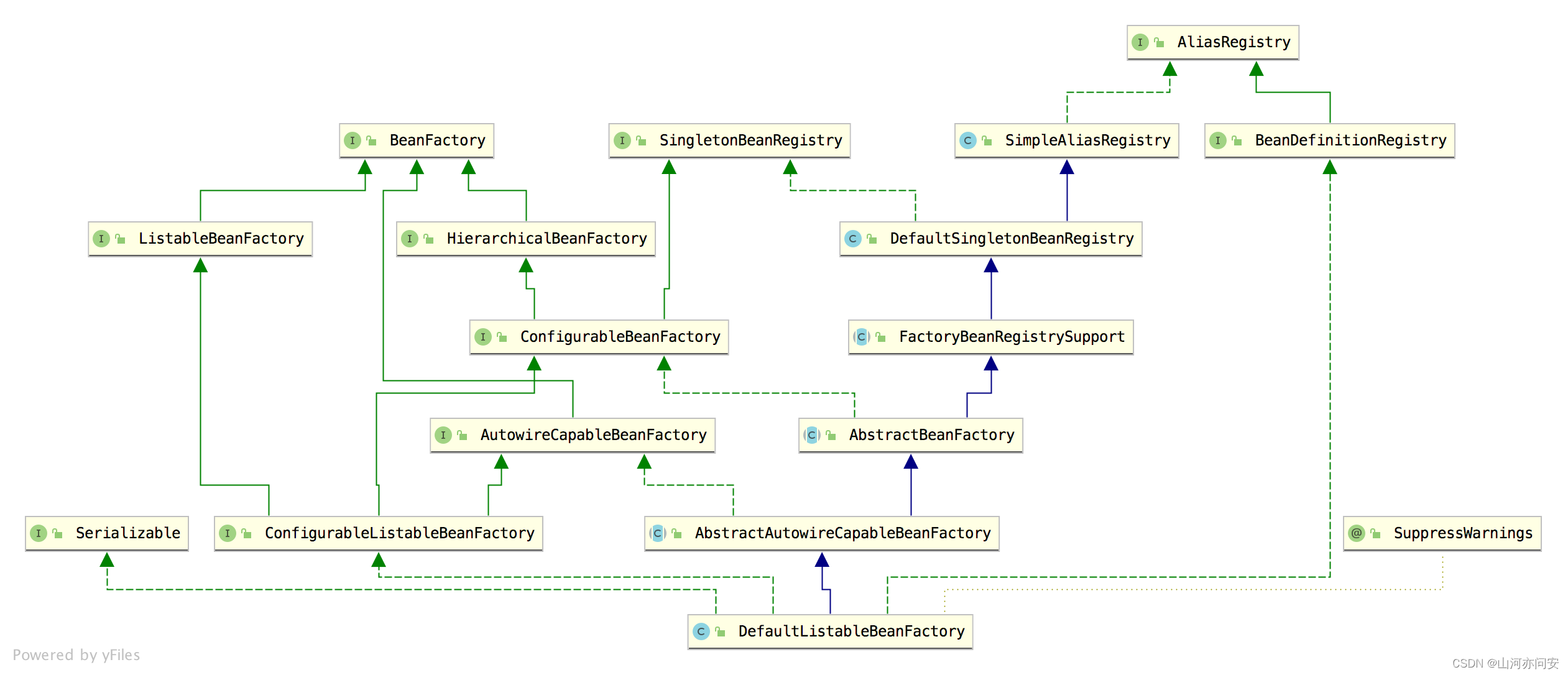
DefaultListableBeanFactory
DefaultListableBeanFactory 是一个完整的、功能成熟的 IoC 容器,如果你的需求很简单,甚至可以直接使用 DefaultListableBeanFactory,如果你的需求比较复杂,那么通过扩展 DefaultListableBeanFactory 的功能也可以达到,…...

NSF服务器
目录 1.简介 1.1 NFS背景介绍 1.2 生产应用场景 2.NFS工作原理 2.1 实例图 2.2 流程 3.NFS的使用 3.1.安装 3.2.配置文件 3.3.主配置文件分析 3.4 实验 服务端: 客户端: 3.5.NFS账户映射 3.5.1.实验2 3.5.2.实验3 4.autofs自动挂载服务…...

10 Go的映射
概述 在上一节的内容中,我们介绍了Go的结构体,包括:定义结构体、声明结构体变量、使用结构体、结构体关联函数、new、组合等。在本节中,我们将介绍Go的映射。Go语言中的映射(Map)是一种无序的键值对集合&am…...

瑞萨e2studio(29)----SPI速率解析
瑞萨e2studio.29--SPI速率解析 概述视频教学时钟配置解析RA4M2的BRR值时钟速率7.5M下寄存器值3K下寄存器值 概述 在嵌入式系统的设计中,串行外设接口(SPI)的通信速率是一个关键参数,它直接影响到系统的性能和稳定性。瑞萨电子的…...
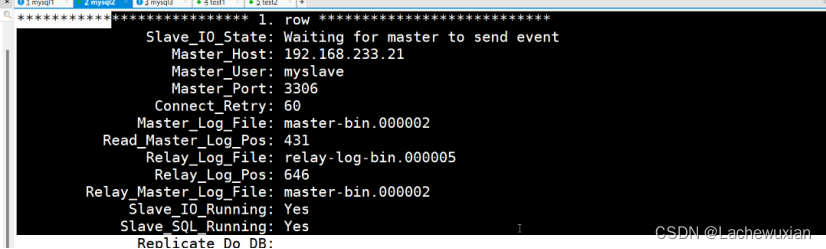
mysql的主从复制,读写分离
主从复制:主mysql的数据,新增,修改,表里的数据都会同步到从mysql上 主从复制的模式: 1 异步复制 mysql 的最常用的复制,只要执行完,客户端提交事务,主mysql 会立即把结果返回给从…...
小米路由器4A千兆版刷入OpenWRT并远程访问
小米路由器4A千兆版刷入OpenWRT并远程访问 文章目录 小米路由器4A千兆版刷入OpenWRT并远程访问前言1. 安装Python和需要的库2. 使用 OpenWRTInvasion 破解路由器3. 备份当前分区并刷入新的Breed4. 安装cpolar内网穿透4.1 注册账号4.2 下载cpolar客户端4.3 登录cpolar web ui管理…...
)
【golang】探索for-range遍历实现原理(slice、map、channel)
for-range for-range其实是正常for循环的一种语法糖,在go语言中可以遍历arr,slice,map和channel等数据结构,但是在一些初学者使用for-range可能会遇见很多坑,这篇文章会带你探索一下for-range中非常有趣的一些实现机制…...

MATLAB | 官方举办的动图绘制大赛 | 第一周赛情回顾
嘿真的又是很久没见了,最近确实有点非常很特别小忙,今天带来一下MATHWORKS官方举办的迷你黑客大赛第三期(MATLAB Flipbook Mini Hack)的最新进展!!目前比赛已经刚好进行了一周,前两届都要求提交280个字符内的代码来生成…...
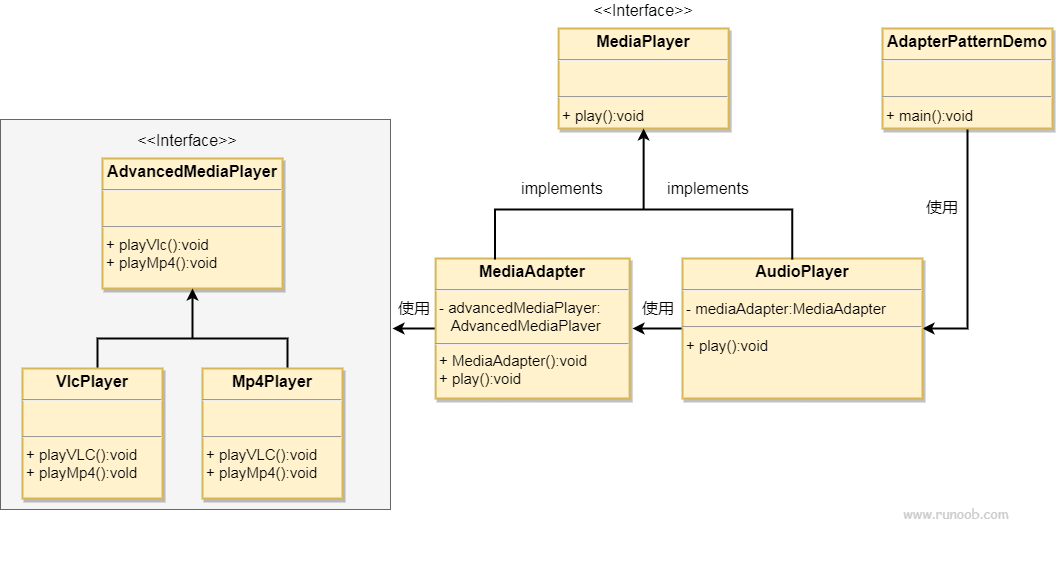
适配器模式 rust和java的实现
文章目录 适配器模式介绍何时使用应用实例优点缺点使用场景 实现java实现rust 实现 rust代码仓库 适配器模式 适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁。这种类型的设计模式属于结构型模式,它结合了两个独立接口的功能…...

竞赛 题目:垃圾邮件(短信)分类 算法实现 机器学习 深度学习 开题
文章目录 1 前言2 垃圾短信/邮件 分类算法 原理2.1 常用的分类器 - 贝叶斯分类器 3 数据集介绍4 数据预处理5 特征提取6 训练分类器7 综合测试结果8 其他模型方法9 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于机器学习的垃圾邮件分类 该项目…...
wpf devexpress项目中添加GridControl绑定数据
本教程讲解了如何添加GridControl到wpf项目中并且绑定数据 原文地址Lesson 1 - Add a GridControl to a Project and Bind it to Data | WPF Controls | DevExpress Documentation 1、使用 DevExpress Template Gallery创建一个新的空白mvvm应用程序,这个项目包括了…...

2023亚太杯数学建模A题思路解析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

