2023亚太杯数学建模A题思路解析
文章目录
- 0 赛题思路
- 1 竞赛信息
- 2 竞赛时间
- 3 建模常见问题类型
- 3.1 分类问题
- 3.2 优化问题
- 3.3 预测问题
- 3.4 评价问题
- 4 建模资料
- 5 最后
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 竞赛信息
2023年第十三届亚太地区大学生数学建模竞赛(以下简称“竞赛”)是北京图象图形学学会主办的亚太地区大学生学科类竞赛,竞赛由亚太地区大学生数学建模竞赛组委会负责组织,欢迎各高等院校按照竞赛章程及有关规定组织同学报名参赛。
2022年第十二届亚太地区大学生数学建模竞赛共有9700支队伍969所高校2万7千多名学生报名参赛。参赛高校覆盖北京大学、清华大学、浙江大学、同济大学、上海交通大学、复旦大学、四川大学、大连理工大学等全部的39所985高校和114所211高校。
除中国大陆高校外,本次参赛队伍还有来自美国的加州大学伯克利分校、约翰斯霍普金斯大学、纽约大学;英国的密德萨斯大学、牛津大学、利物浦大学、诺丁汉大学、爱丁堡大学;德国的亚琛工业大学、 北黑森应用技术大学;俄罗斯的圣彼得堡国立建筑大学;澳大利亚的墨尔本大学、悉尼大学;马来西亚的马来亚大学;日本的東北大学;法国的巴黎先贤祠-阿萨斯大学;澳门地区的澳门城市大学、澳门科技大学、澳门理工学院、澳门大学;香港地区的北京师范大学-香港浸会大学联合国际学院、香港中文大学、香港科技大学、香港理工大学;中外合作的宁波诺丁汉大学、深圳北理莫斯科大学、西安交通利物浦大学等高校。
目前竞赛具有较高的国际影响力,在国内高校中是作为美赛热身赛、保研加分、综合测评加分、创新奖学金等评定竞赛之一。
2 竞赛时间
报名结束时间:2023年11月22日
比赛开始时间:2023年11月23日(周四)6:00
比赛结束时间:2023年11月27日(周一)9:00
3 建模常见问题类型
趁现在赛题还没更新,A君给大家汇总一下数学建模经常使用到的数学模型,题目八九不离十基本属于一下四种问题,对应的解法A君也相应给出
分别为:
分类模型
优化模型
预测模型
评价模型
3.1 分类问题
判别分析:
又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
其基本原理是按照一定的判别准则,建立一个或多个判别函数;用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标;据此即可确定某一样本属于何类。当得到一个新的样品数据,要确定该样品属于已知类型中哪一类,这类问题属于判别分析问题。
聚类分析:
聚类分析或聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集,这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。
聚类分析本身不是某一种特定的算法,而是一个大体上的需要解决的任务。它可以通过不同的算法来实现,这些算法在理解集群的构成以及如何有效地找到它们等方面有很大的不同。
神经网络分类:
BP 神经网络是一种神经网络学习算法。其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。RBF(径向基)神经网络:径向基函数(RBF-Radial Basis Function)神经网络是具有单隐层的三层前馈网络。它模拟了人脑中局部调整、相互覆盖接收域的神经网络结构。感知器神经网络:是一个具有单层计算神经元的神经网络,网络的传递函数是线性阈值单元。主要用来模拟人脑的感知特征。线性神经网络:是比较简单的一种神经网络,由一个或者多个线性神经元构成。采用线性函数作为传递函数,所以输出可以是任意值。自组织神经网络:自组织神经网络包括自组织竞争网络、自组织特征映射网络、学习向量量化等网络结构形式。K近邻算法: K最近邻分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
3.2 优化问题
线性规划:
研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。它是运筹学的一个重要分支,广泛应用于生产计划、物流运输、资源分配、金融投资等领域。建模方法:列出约束条件及目标函数;画出约束条件所表示的可行域;在可行域内求目标函数的最优解及最优值。
整数规划:
规划中的变量(全部或部分)限制为整数,称为整数规划。若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。一类要求问题的解中的全部或一部分变量为整数的数学规划。从约束条件的构成又可细分为线性,二次和非线性的整数规划。
非线性规划:
非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。非线性规划研究一个 n元实函数在一组等式或不等式的约束条件下的极值问题,且 目标函数和约束条件至少有一个是未知量的非线性函数。目标函数和约束条件都是 线性函数的情形则属于线性规划。
动态规划:
包括背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等。
动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
多目标规划:
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。任何多目标规划问题,都由两个基本部分组成:
(1)两个以上的目标函数;
(2)若干个约束条件。有n个决策变量,k个目标函数, m个约束方程,则:
Z=F(X)是k维函数向量,Φ(X)是m维函数向量;G是m维常数向量;
3.3 预测问题
回归拟合预测
拟合预测是建立一个模型去逼近实际数据序列的过程,适用于发展性的体系。建立模型时,通常都要指定一个有明确意义的时间原点和时间单位。而且,当t趋向于无穷大时,模型应当仍然有意义。将拟合预测单独作为一类体系研究,其意义在于强调其唯“象”性。一个预测模型的建立,要尽可能符合实际体系,这是拟合的原则。拟合的程度可以用最小二乘方、最大拟然性、最小绝对偏差来衡量。
灰色预测
灰色预测是就灰色系统所做的预测。是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
马尔科夫预测:是一种可以用来进行组织的内部人力资源供给预测的方法.它的基本 思想是找出过去人事变动的 规律,以此来推测未来的人事变动趋势.转换矩阵实际上是转换概率矩阵,描述的是组织中员工流入,流出和内部流动的整体形式,可以作为预测内部劳动力供给的基础.
BP神经网络预测
BP网络(Back-ProPagation Network)又称反向传播神经网络, 通过样本数据的训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出。它是一种应用较为广泛的神经网络模型,多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
支持向量机法
支持向量机(SVM)也称为支持向量网络[1],是使用分类与回归分析来分析数据的监督学习模型及其相关的学习算法。在给定一组训练样本后,每个训练样本被标记为属于两个类别中的一个或另一个。支持向量机(SVM)的训练算法会创建一个将新的样本分配给两个类别之一的模型,使其成为非概率二元线性分类器(尽管在概率分类设置中,存在像普拉托校正这样的方法使用支持向量机)。支持向量机模型将样本表示为在空间中的映射的点,这样具有单一类别的样本能尽可能明显的间隔分开出来。所有这样新的样本映射到同一空间,就可以基于它们落在间隔的哪一侧来预测属于哪一类别。
3.4 评价问题
层次分析法
是指将一个复杂的 多目标决策问题 作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
优劣解距离法
又称理想解法,是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解,即各指标的最大值和最小值,通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和远离负理想解的程度,来对方案进行排序,从而选出最优方案。
模糊综合评价法
是一种基于模糊数学的综合评标方法。 该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。 它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
灰色关联分析法(灰色综合评价法)
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
典型相关分析法:是对互协方差矩阵的一种理解,是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
主成分分析法(降维)
是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上用来降维的一种方法。
因子分析法(降维)
因子分析是指研究从变量群中提取共性因子的统计技术。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性,一科成绩好的学生,往往其他各科成绩也比较好,从而推想是否存在某些潜在的共性因子,或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
BP神经网络综合评价法
是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
4 建模资料
资料分享: 最强建模资料


5 最后
相关文章:

2023亚太杯数学建模A题思路解析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...
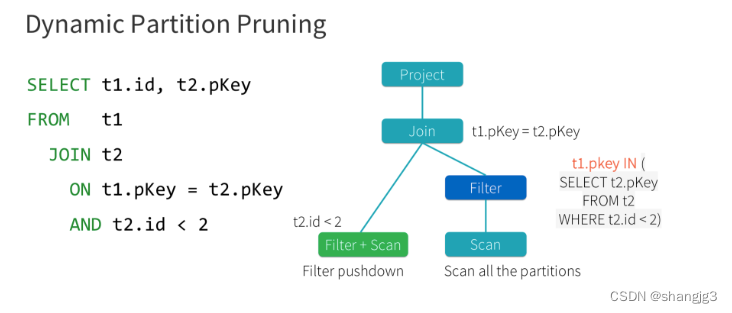
Spark3.0中的AOE、DPP和Hint增强
1 Spark3.0 AQE Spark 在 3.0 版本推出了 AQE(Adaptive Query Execution),即自适应查询执行。AQE 是 Spark SQL 的一种动态优化机制,在运行时,每当 Shuffle Map 阶段执行完毕,AQE 都会结合这个阶段的统计信…...

算法笔记-第五章-质因子分解
算法笔记-第五章-质因子分解 小试牛刀质因子2的个数丑数 质因子分解最小最大质因子约数个数 小试牛刀 质因子2的个数 #include<cstdio> int main() {int n; scanf_s("%d", &n); int count 0; while (n % 2 0) {count; n / 2; }printf("%…...
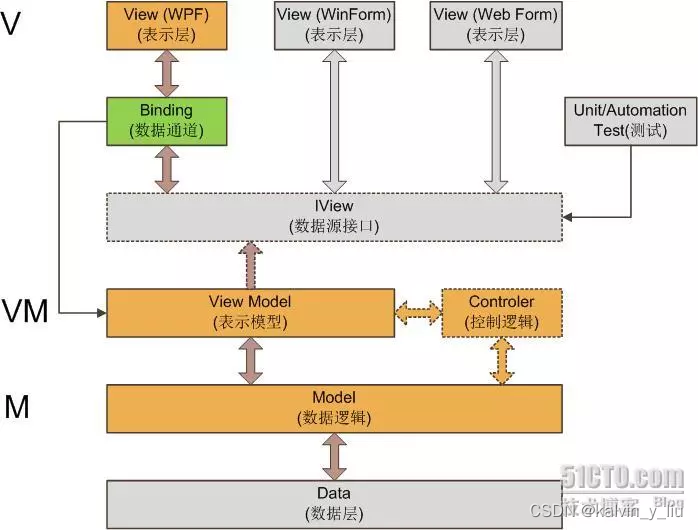
适用于WPF的设计模式
适用于WPF的设计模式 讨论“XAML能不能写逻辑代码”这个问题。我发现这是个有歧义的问题。这个问题可以有两种意思: XAML能不能用来写逻辑代码? XAML文件里能不能包含逻辑代码? 对于第一种意思——XAML是一种声明性语言,就是用来…...

C++与多态
多态的本质是允许对象以其实际类型的行为方式来操作,而不仅仅是其静态类型所声明的方式。 多态是面向对象编程中的一种核心概念,它允许对象根据其具体类型执行相应的操作,而不是其声明的类型。我们可以使用一个经典的动物的例子来说明这一点。…...
ios 对话框UIAlertController放 tableview
//强弱引用 #define kWeakSelf(type)__weak typeof(type)weak##type type; -(void) showUIAlertTable {kWeakSelf(self)UIAlertController *alert [UIAlertController alertControllerWithTitle:NSLocalizedString("select_stu", nil) message:nil prefer…...

警告:新版Outlook会向微软发送密码、邮件和其他数据
新的免费Outlook会将敏感数据发送给 Microsoft。 在没有通知或询问的情况下,Microsoft 授予自己对新 Outlook 用户的 IMAP 和 SMTP 访问数据的完全访问权限。也就是说,当用户设置 IMAP 帐户时,新的 Outlook 会将访问数据和服务器信息发送给 …...

数据结构C语言--基础实验
实验1 线性表的顺序实现 1.!顺序表的倒置 /**********************************/ /*文件名称:lab1-01.c */ /**********************************/ /*基于sequlist.h中定义的顺序表,编写算法函数reverse(sequence_list *L)&…...

wireshark抓包并进行Eigrp网络协议分析
路由协议 Eigrp EIGRP:Enhanced Interior Gateway Routing Protocol 即 增强内部网关路由协议。也翻译为 加强型内部网关路由协议。 EIGRP是Cisco公司的私有协议(2013年已经公有化)。 EIGRP结合了链路状态和距离矢量型路由选择协议的Cisco专用协议&a…...
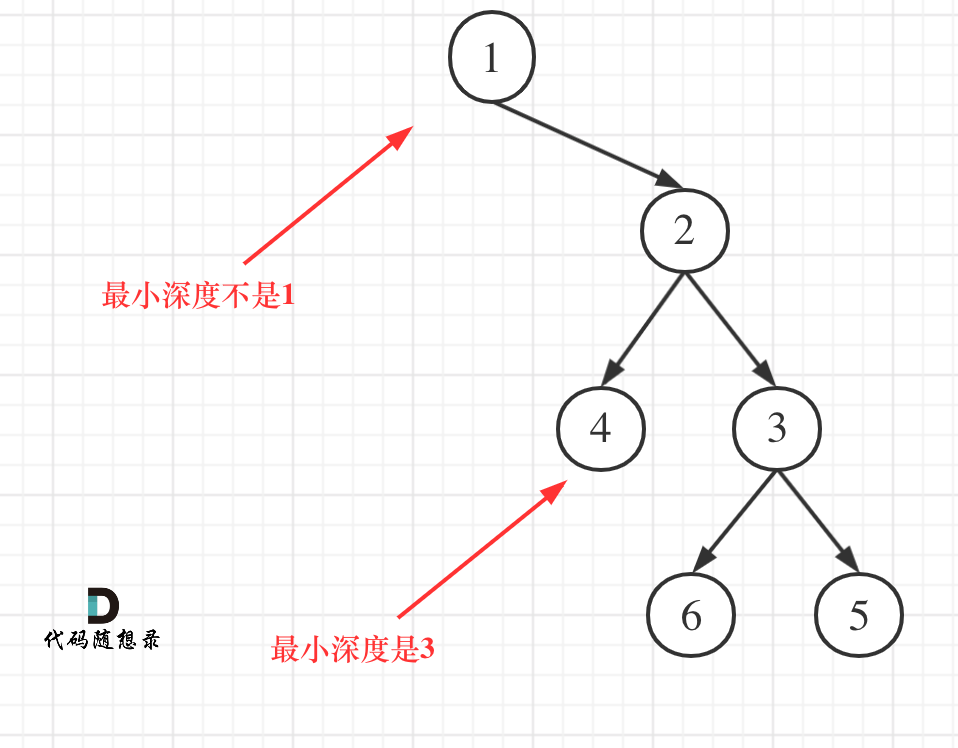
力扣刷题-二叉树-二叉树的层序遍历(相关题目总结)
思路 层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。 需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的…...

fundamental notes in 3D math
平面方程 a x b y c z d axbycz d axbyczd, 法向量 a , b , c a,b,c a,b,c, 点到平面的距离为 d / s q r t ( a 2 b 2 c 2 ) d / sqrt(a^2 b^2 c^2) d/sqrt(a2b2c2) , 距离可为正, 为负, 为正表示跟法向量方向一致, 为负表示相反 点 ( x o , y o , z o ) (x_o, y_o, z…...

【Java 进阶篇】JQuery DOM操作:舞动网页的属性魔法
在前端的舞台上,属性操作是我们与HTML元素进行互动的关键步骤之一。而JQuery,这位前端开发的巫师,通过简洁而强大的语法,为我们提供了便捷的属性操作工具。在这篇博客中,我们将深入研究JQuery DOM操作中的属性操作&…...
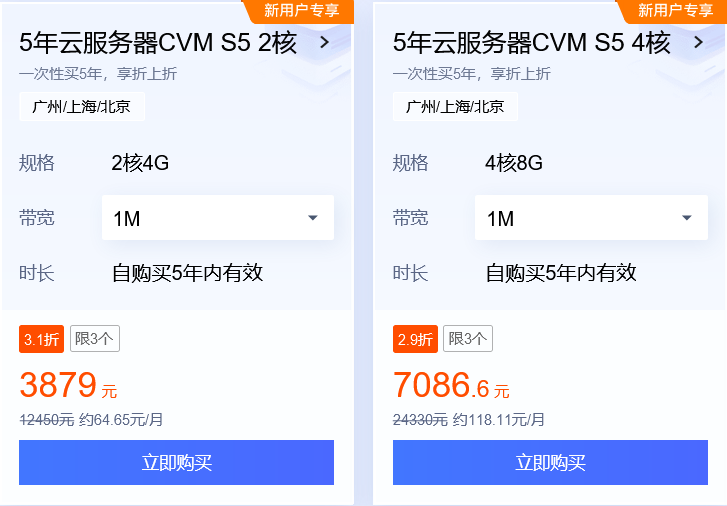
腾讯云5年云服务器还有吗?腾讯云5年时长服务器入口在哪?
如果你是一名企业家或者是一个热衷于数字化转型的创业者,那么腾讯云最近推出的一项优惠活动绝对不会让你无动于衷。现在,腾讯云正在大力推广一项5年特价云服务器活动,只需要花费3879元,你就可以享受到腾讯云提供的优质服务。 腾讯…...

odoo在iot领域的发展情况
Odoo 是一个全面的集成商业管理软件套装,主要提供企业资源规划 (ERP)、客户关系管理 (CRM)、电子商务、会计、库存管理等功能。在 IoT(物联网)领域,Odoo 侧重于通过提供一个中心化的平台来整合多方面的业务流程,包括生…...

Paas-云原生-容器-编排-持续部署
了解云原生 云原生架构让企业的基础设施,从简单的资源池化,转向以应用为中心,为应用赋能的敏捷、自运维、安全的云原生基础设施。以应用为中心的云原生基础设置,可以支持多种类型的应用,如微服务应用,中间件应用和AI 应用;可以提升应用交付效率,简化应用管理的复杂度;…...

sass 生成辅助色
背景 一个按钮往往有 4 个状态。 默认状态hover鼠标按下禁用状态 为了表示这 4 个状态,需要设置 4 个颜色来提示用户。 按钮类型一般有 5 个: 以 primary 类型按钮为例,设置它不同状态下的颜色: <button class"btn…...
DevEco Studio开发工具下载、安装(HarmonyOS开发)_For Mac
一、说明 初学HarmonyOS开发,DevEco Studio开发工具的安装和使用是必须的。 (注:不多废话,跟着下面流程操作下载、安装DevEco Studio即可。) 二、下载DevEco Studio 1.官网下载地址: https://developer.…...
按键精灵中的字符串常用的场景
在使用按键精灵编写脚本时,与字符串有关的场景有以下几种: 1. 用时间字符串记录脚本使用截止使用时间 Dim localTime "2023-11-12 00:15:14" Dim networkTime GetNetworkTime() TracePrint networkTime If networkTime > localTime The…...

python数据结构与算法-01_抽象数据类型和面向对象编程
Python 一切皆对象 举个例子,在 python 中我们经常使用的 list l list() # 实例化一个 list 对象 l l.append(1) # 调用 l 的 append 方法 l.append(2) l.remove(1) print(len(l)) # 调用对象的 __len__ 方法在后面实现新的数据类型时,我们将…...

纯手写 模态框、消息弹框、呼吸灯
在有些做某些网页中,应用不想引用一些前端框架,对于一些比较常用的插件可以纯手写实现 1、模态框 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>Water Ripple Effect</title> <style…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
