力扣刷题-二叉树-二叉树的层序遍历(相关题目总结)
思路
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:
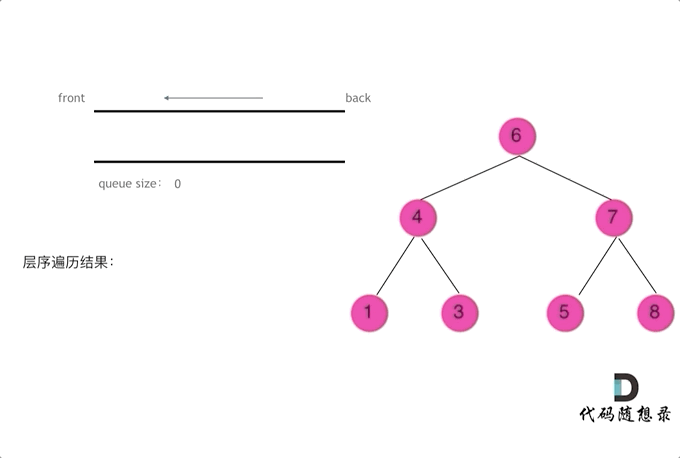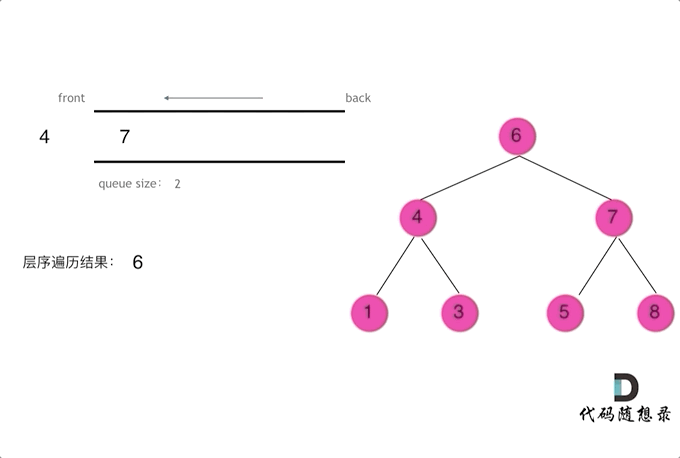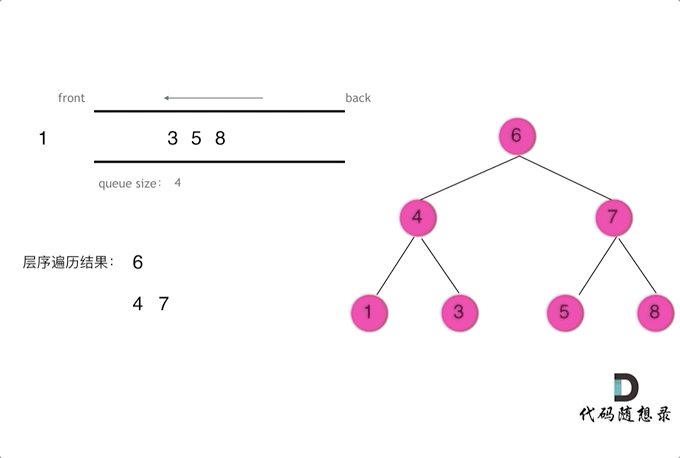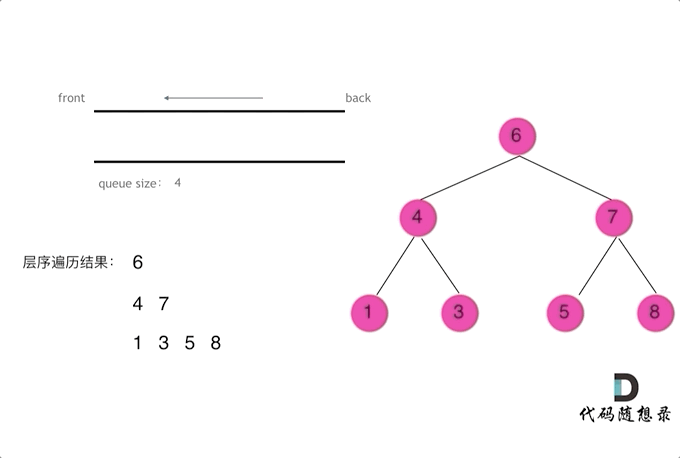
这样就实现了层序从左到右遍历二叉树。
参考:https://www.programmercarl.com/0102.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%B1%82%E5%BA%8F%E9%81%8D%E5%8E%86.html
102 层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。

利用长度法
# 注意结果的返回形式是每层作为一个列表
# 法一 长度法from collections import deque
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def levelOrder(self, root):""":type root: TreeNode:rtype: List[List[int]]"""# 注意判断是否为空if not root:return []result = [] # 最终结果列表 里面会存储每一层的遍历结果queue = deque([root]) # 采用队列来模拟while queue: # 当queue为空 终止level_result = [] # 每一层结果for _ in range(len(queue)): # queue中记录的是每一层进入队列的元素 所以遍历其长度 来获取元素值cur = queue.popleft()level_result.append(cur.val)if cur.left: # 左孩子 就是第二层了queue.append(cur.left)if cur.right:queue.append(cur.right)result.append(level_result)return result
递归法
每次写递归,都按照这三要素来写,可以保证大家写出正确的递归算法!
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
# 法二 递归法
from collections import deque
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def levelOrder(self, root):if not root:return []levels = []self.helper(root, 0, levels)return levelsdef helper(self, node, level, levels):if not node:returnif len(levels) == level:levels.append([]) # 每层开始 用[]初始化levels[level].append(node.val)self.helper(node.left, level+1, levels)self.helper(node.right, level+1, levels)
确定递归函数的参数和返回值:当前节点;第几层,结果存储列表
确定终止条件:当当前节点不存在的时候 直接return(终止本次)
确定单层递归的逻辑:
if len(levels) == level:
levels.append([]) # 每层开始 用[]初始化
levels[level].append(node.val)
107. 二叉树的层序遍历 II
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
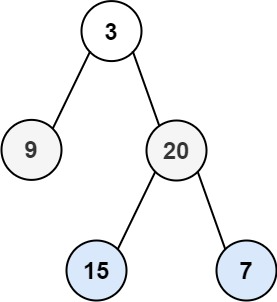
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
其实相当于就是上一题结果做一下翻转。
from collections import dequeclass TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def levelOrderBottom(self, root):""":type root: TreeNode:rtype: List[List[int]]"""if not root:return []result = []queue = deque([root])while queue:level_result = []for _ in range(len(queue)):cur = queue.popleft()level_result.append(cur.val)if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)result.append(level_result)return result[::-1]
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
思路:其实就是层序遍历每一层遍历结果的最后一个元素
from collections import deque
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def rightSideView(self, root):""":type root: TreeNode:rtype: List[int]"""if not root:return []levels = []self.helper(root, 0, levels)result = []for item in levels:result.append(item[len(item)-1])return resultdef helper(self, node, level, levels):if not node:return if len(levels) == level:levels.append([])levels[level].append(node.val)self.helper(node.left, level+1, levels)self.helper(node.right, level+1, levels)
637. 二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:
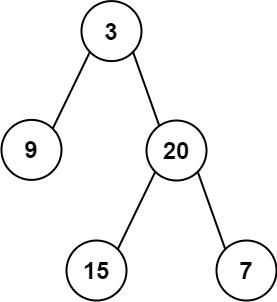
输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11]
思路:就是对每一层结果 取平均 注意需要用float!!!
from collections import dequeclass TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def averageOfLevels(self, root):""":type root: TreeNode:rtype: List[float]"""if not root:return []result = []queue = deque([root])while queue:level_result = []for _ in range(len(queue)):cur = queue.popleft()level_result.append(cur.val)if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)result.append(level_result)final = [(sum(item)/float(len(item))) for item in result] # 注意要加上float 因为python中 / 是整除return final
429. N 叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:
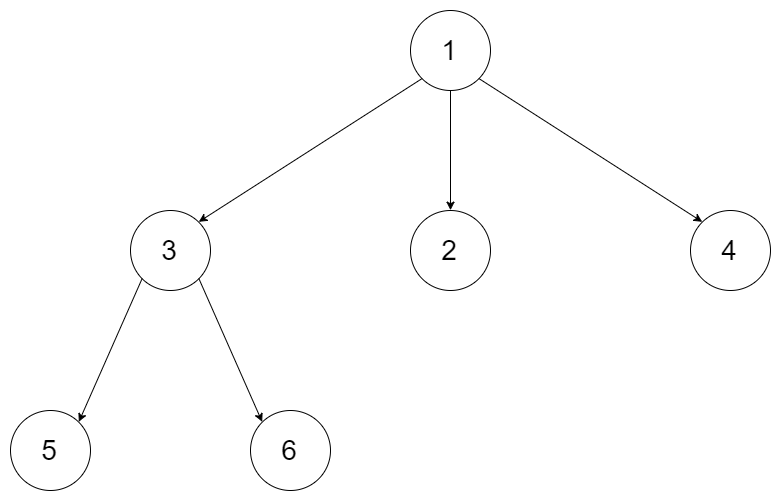
输入:root = [1,null,3,2,4,null,5,6]
输出:[[1],[3,2,4],[5,6]]
思路:N叉树 每个节点存在多个孩子 所以要采用遍历方式
from collections import deque class Node(object):def __init__(self, val=None, children=None):self.val = valself.children = childrenclass Solution(object):def levelOrder(self, root):""":type root: Node:rtype: List[List[int]]"""if not root:return []result = []queue = deque([root])while queue:level_result = []for _ in range(len(queue)):node = queue.popleft()level_result.append(node.val)for child in node.children: # 因为有多个孩子 所以采用遍历方式queue.append(child)result.append(level_result)return result
时间复杂度:O(n),其中 n 是树中包含的节点个数。在广度优先搜索的过程中,我们需要遍历每一个节点恰好一次。
空间复杂度:O(n),即为队列需要使用的空间。在最坏的情况下,树只有两层,且最后一层有 n−1 个节点,此时就需要 O(n) 的空间。
515. 在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:
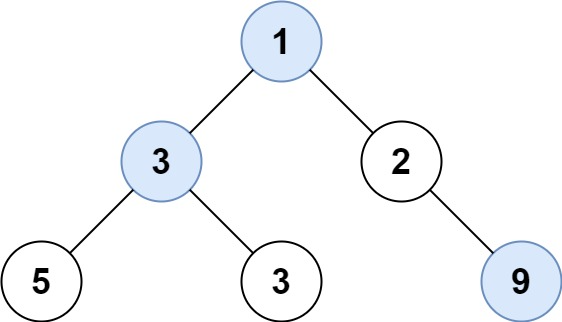
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
思路:就是求每一层遍历结果的最大值
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def largestValues(self, root):""":type root: TreeNode:rtype: List[int]"""if not root:return []result = []queue = deque([root])while queue:level_result = []for _ in range(len(queue)):cur = queue.popleft()level_result.append(cur.val)if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)result.append(level_result)final = [max(item) for item in result] # 求最大return final
(※)116. 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:
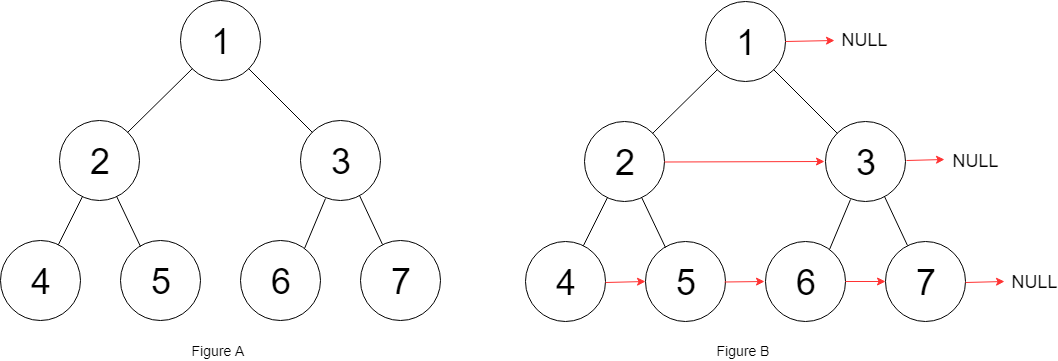
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,‘#’ 标志着每一层的结束。
# # 注意节点定义
class Node(object):def __init__(self, val=0, left=None, right=None, next=None):self.val = valself.left = leftself.right = right self.next = next # 多了一个nextfrom collections import dequeclass Solution:def connect(self, root):if not root:return root # 因为最终返回的是整棵树# 初始化队列同时将第一层节点加入队列中,即根节点Q = collections.deque([root])# 外层的 while 循环迭代的是层数while Q:# 记录当前队列大小size = len(Q)# 遍历这一层的所有节点for i in range(size):# 从队首取出元素node = Q.popleft()# 连接 比较巧妙if i < size - 1: # 题目说了 初始状态下 所有的Next指针都设置为 nullnode.next = Q[0] # 比如2出来 指向队列里面第一个元素 就是3# 拓展下一层节点if node.left:Q.append(node.left)if node.right:Q.append(node.right)# 返回根节点return root117 填充每个节点的下一个右侧节点指针 II
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:
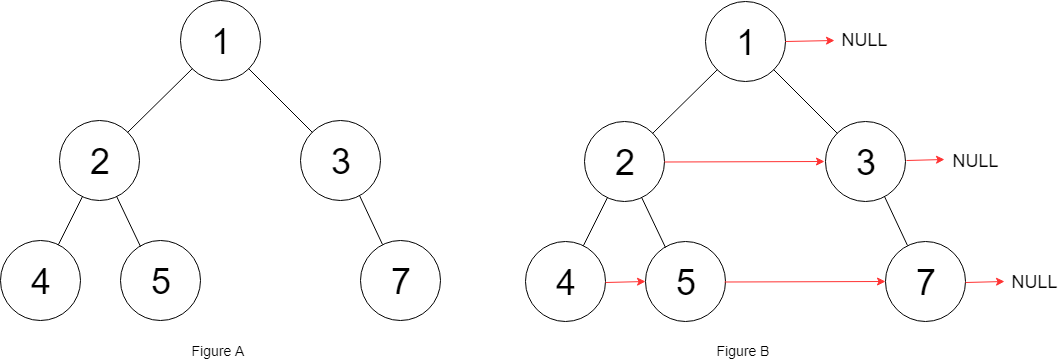
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),‘#’ 表示每层的末尾。
思路:其实和上一题是一样,上一题是完美/全二叉树,本题不是,但是是一样的做法。
from collections import dequeclass Node(object):def __init__(self, val=0, left=None, right=None, next=None):self.val = valself.left = leftself.right = rightself.next = nextclass Solution(object):def connect(self, root):""":type root: Node:rtype: Node"""if not root:return rootqueue = deque([root])while queue:size = len(queue)for i in range(size):cur = queue.popleft()if i < size - 1:cur.next = queue[0]if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)return root
104. 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
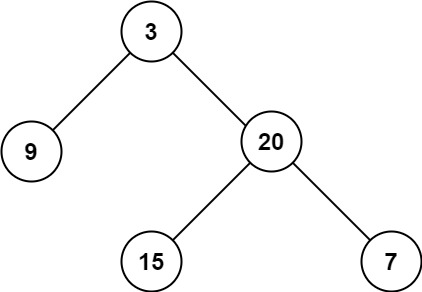
输入:root = [3,9,20,null,null,15,7]
输出:3
思路:按照层序遍历 有多少层(最大深度)即 有多少个嵌套列表
层次遍历
from collections import dequeclass TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0result = []queue = deque([root])while queue:level_result = []for _ in range(len(queue)):cur = queue.popleft()level_result.append(cur.val)if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)result.append(level_result)return len(result) # 里面多少嵌套列表 即为最大深度
递归
递归第一点:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
递归第二点:如果为空节点的话,就返回0,表示高度为0。
递归第三点:
**先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1 **(加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。(也就是高度)
class solution:def maxdepth(self, root: treenode) -> int:return self.getdepth(root)def getdepth(self, node):if not node:return 0leftdepth = self.getdepth(node.left)rightdepth = self.getdepth(node.right)depth = max(leftdepth, rightdepth) + 1return depth
精简版:
class solution:def maxdepth(self, root: treenode) -> int:if not root:return 0return 1 + max(self.maxdepth(root.left), self.maxdepth(root.right))
559. N 叉树的最大深度
层次遍历
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例 1:
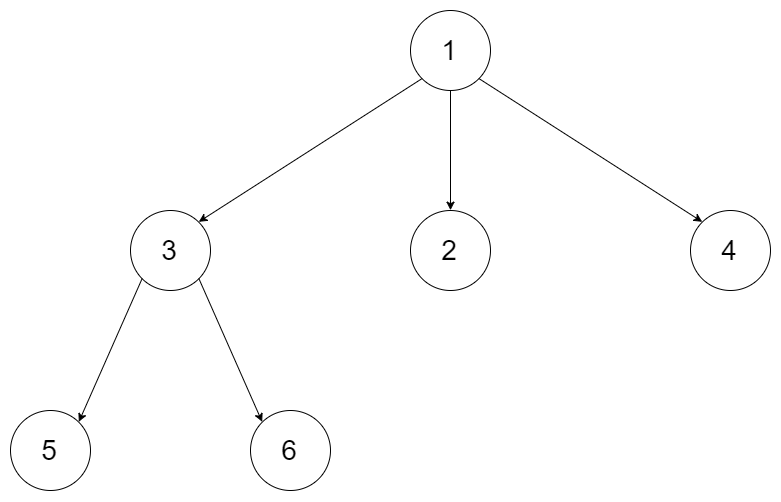
输入:root = [1,null,3,2,4,null,5,6]
输出:3
# Definition for a Node.
class Node(object):def __init__(self, val=None, children=None):self.val = valself.children = childrenfrom collections import deque
class Solution(object):def maxDepth(self, root):""":type root: Node:rtype: int"""if not root:return 0result = []queue = deque([root])while queue:level_result = []for _ in range(len(queue)):cur = queue.popleft()level_result.append(cur.val)for child in cur.children: # 特别之处queue.append(child)result.append(level_result)return len(result)
递归
class Solution:def maxDepth(self, root: 'Node') -> int:if not root:return 0max_depth = 1for child in root.children:max_depth = max(max_depth, self.maxDepth(child) + 1)return max_depth
(※)111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:2
层序遍历法
# 层序遍历法
class Solution(object):def minDepth(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0queue = deque([(root, 1)]) # 每个元素是元组 一个是树元素值 一个是最小深度 比较巧妙while queue:cur, min_depth = queue.popleft()if not cur.left and not cur.right:return min_depthif cur.left:queue.append((cur.left, min_depth+1))if cur.right:queue.append((cur.right, min_depth+1))return 0
时间复杂度:O(N) 因为每个结点会访问一次
空间复杂度:O(N)在层序遍历法中空间复杂度主要取决于队列的开销,队列中的元素个数不会超过树的节点数。
递归法
注意这块和最大深度不一样,如下是错误代码:

这个代码就犯了此图中的误区:
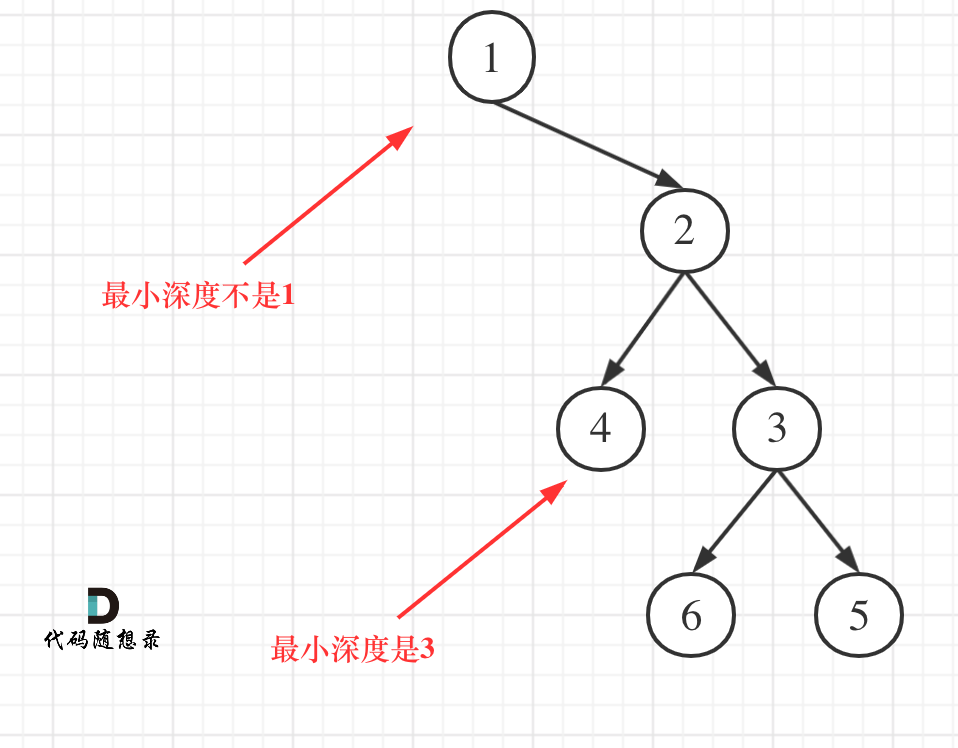
如果这么求的话,没有左孩子的分支会算为最短深度。
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
# 递归法
class Solution(object):def minDepth(self, root):""":type root: TreeNode:rtype: int"""return self.getDepth(root)def getDepth(self, node):if node is None:return 0leftDepth = self.getDepth(node.left) # 左rightDepth = self.getDepth(node.right) # 右# 当一个左子树为空,右不为空,这时并不是最低点if node.left is None and node.right is not None:return 1 + rightDepth# 当一个右子树为空,左不为空,这时并不是最低点if node.left is not None and node.right is None:return 1 + leftDepthresult = 1 + min(leftDepth, rightDepth)return result
时间复杂度:O(N),其中 N 是树的节点数。对每个节点访问一次。
空间复杂度:O(N)/O(H) 其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关,空间复杂度为 O(logN)
相关文章:

力扣刷题-二叉树-二叉树的层序遍历(相关题目总结)
思路 层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。 需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的…...

fundamental notes in 3D math
平面方程 a x b y c z d axbycz d axbyczd, 法向量 a , b , c a,b,c a,b,c, 点到平面的距离为 d / s q r t ( a 2 b 2 c 2 ) d / sqrt(a^2 b^2 c^2) d/sqrt(a2b2c2) , 距离可为正, 为负, 为正表示跟法向量方向一致, 为负表示相反 点 ( x o , y o , z o ) (x_o, y_o, z…...

【Java 进阶篇】JQuery DOM操作:舞动网页的属性魔法
在前端的舞台上,属性操作是我们与HTML元素进行互动的关键步骤之一。而JQuery,这位前端开发的巫师,通过简洁而强大的语法,为我们提供了便捷的属性操作工具。在这篇博客中,我们将深入研究JQuery DOM操作中的属性操作&…...
腾讯云5年云服务器还有吗?腾讯云5年时长服务器入口在哪?
如果你是一名企业家或者是一个热衷于数字化转型的创业者,那么腾讯云最近推出的一项优惠活动绝对不会让你无动于衷。现在,腾讯云正在大力推广一项5年特价云服务器活动,只需要花费3879元,你就可以享受到腾讯云提供的优质服务。 腾讯…...

odoo在iot领域的发展情况
Odoo 是一个全面的集成商业管理软件套装,主要提供企业资源规划 (ERP)、客户关系管理 (CRM)、电子商务、会计、库存管理等功能。在 IoT(物联网)领域,Odoo 侧重于通过提供一个中心化的平台来整合多方面的业务流程,包括生…...

Paas-云原生-容器-编排-持续部署
了解云原生 云原生架构让企业的基础设施,从简单的资源池化,转向以应用为中心,为应用赋能的敏捷、自运维、安全的云原生基础设施。以应用为中心的云原生基础设置,可以支持多种类型的应用,如微服务应用,中间件应用和AI 应用;可以提升应用交付效率,简化应用管理的复杂度;…...

sass 生成辅助色
背景 一个按钮往往有 4 个状态。 默认状态hover鼠标按下禁用状态 为了表示这 4 个状态,需要设置 4 个颜色来提示用户。 按钮类型一般有 5 个: 以 primary 类型按钮为例,设置它不同状态下的颜色: <button class"btn…...
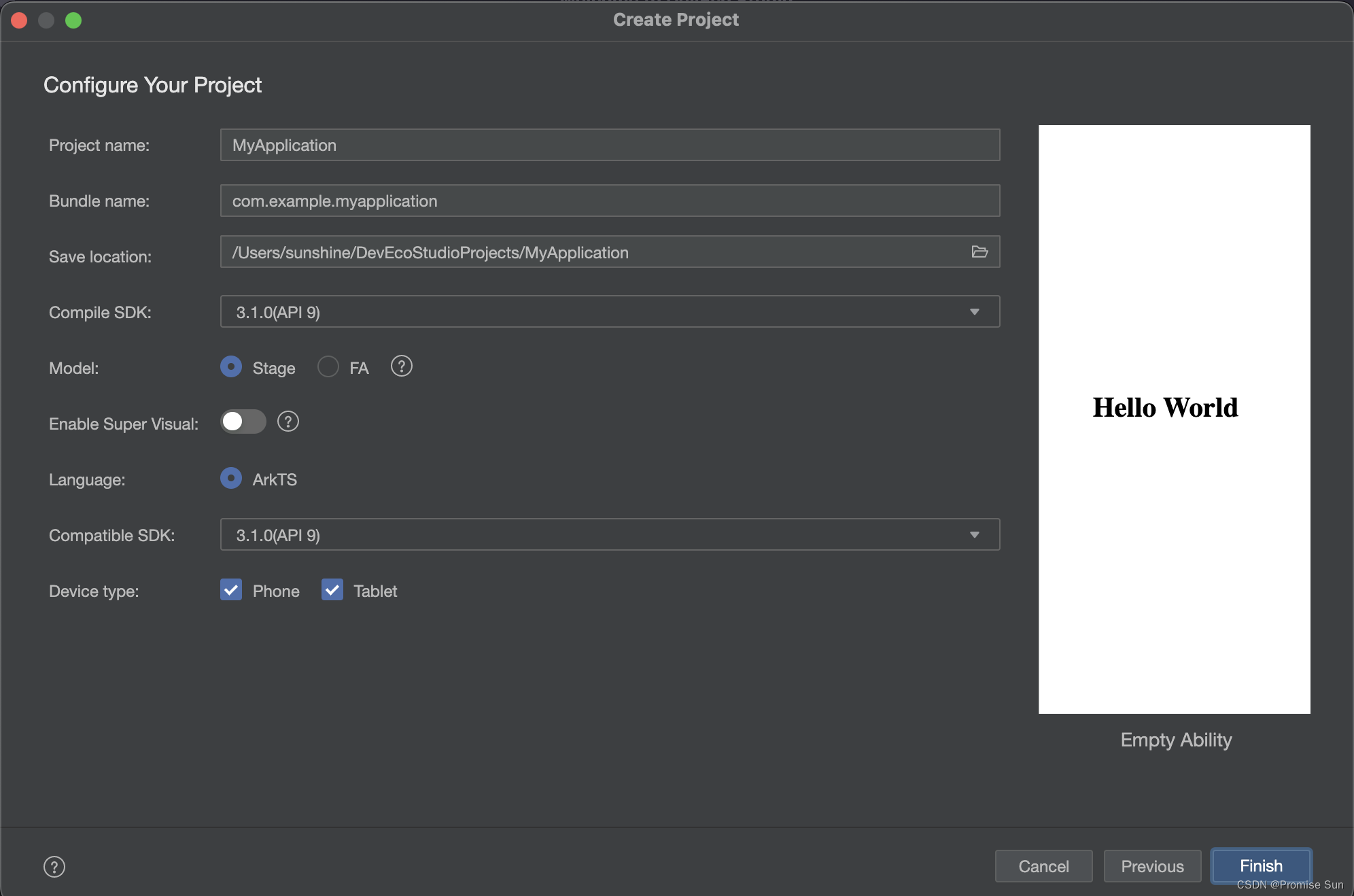
DevEco Studio开发工具下载、安装(HarmonyOS开发)_For Mac
一、说明 初学HarmonyOS开发,DevEco Studio开发工具的安装和使用是必须的。 (注:不多废话,跟着下面流程操作下载、安装DevEco Studio即可。) 二、下载DevEco Studio 1.官网下载地址: https://developer.…...
按键精灵中的字符串常用的场景
在使用按键精灵编写脚本时,与字符串有关的场景有以下几种: 1. 用时间字符串记录脚本使用截止使用时间 Dim localTime "2023-11-12 00:15:14" Dim networkTime GetNetworkTime() TracePrint networkTime If networkTime > localTime The…...

python数据结构与算法-01_抽象数据类型和面向对象编程
Python 一切皆对象 举个例子,在 python 中我们经常使用的 list l list() # 实例化一个 list 对象 l l.append(1) # 调用 l 的 append 方法 l.append(2) l.remove(1) print(len(l)) # 调用对象的 __len__ 方法在后面实现新的数据类型时,我们将…...

纯手写 模态框、消息弹框、呼吸灯
在有些做某些网页中,应用不想引用一些前端框架,对于一些比较常用的插件可以纯手写实现 1、模态框 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>Water Ripple Effect</title> <style…...

windows安装composer并更换国内镜像
第一步、官网下载 下载地址 Composer安装https://getcomposer.org/Composer-Setup.exe第二步、双击安装即可 第三步选择 php安装路径并配置path 第四步、 composer -v查看安装是否成功,出现成功界面 第五步、查看镜像地址并更换(composer国内可能较慢…...

c++ basic_string 和string区别
在C中,basic_string 是一个模板类,而 string 是 basic_string 的一个具体实例化,即 basic_string<char>。basic_string 模板类被设计为支持多种字符类型,而 string 是其中一种特定字符类型的字符串类。 具体来说࿰…...
)
怎么在uni-app中使用Vuex 简单demo,通俗易懂(第二篇)
Vuex是Vue.js的官方状态管理库,可以帮助我们更好地管理和维护复杂状态和数据共享。在Vuex中,整个应用的状态被集中到一个单一的状态树中,这个状态树包含了所有的共享状态和数据。通过状态管理模块、getter、mutation、action等机制࿰…...

相机专业模型详解,各个参数作用,专业模式英文全称和缩写
ISO(感光度) 全称: International Organization for Standardization缩写: ISO Shutter Speed(快门速度) 全称: Shutter Speed缩写: SS Aperture(光圈大小) 全…...

将随机数设成3407,让你的深度学习模型再涨一个点!文再附3种随机数设定方法
随机数重要性 深度学习已经在计算机视觉领域取得了巨大的成功,但我们是否曾想过为什么同样的模型在不同的训练过程中会有不同的表现?为什么使用同样的代码,就是和别人得到的结果不一样?怎么样才能保证自己每次跑同一个实验得到的…...

Spring后端HttpClient实现微信小程序登录
这是微信官方提供的时序图。我们需要关注的是前后端的交互,以及服务端如何收发网络请求。 小程序端 封装基本网络请求 我们先封装一个基本的网络请求。 const baseUrl"localhost:8080" export default{sendRequsetAsync } /* e url:目标页…...

Linux下部署MySQL-MHA环境
目前的环境如下:centos7 有四台虚拟机,20,21,22,23 20为master,21,22,23 为20的从库,21 为管理节点。 搭建MySQL主从复制的,可以参考我之前的文章 MHA&#…...
开发笔记 20231114-阿里云mysql外部访问)
DaoWiki(基于Django)开发笔记 20231114-阿里云mysql外部访问
文章目录 创建mysql用户,用户远程访问配置阿里云安全策略下载安装mysql workbench 创建mysql用户,用户远程访问 创建用户 CREATE USER dao_wiki% IDENTIFIED BY password;授权访问dao_wiki数据库 GRANT ALL PRIVILEGES ON dao_wiki.* TO dao_wiki%; F…...
【UE5】 虚拟制片教程
目录 效果 步骤 一、下载素材 二、将视频转成PNG序列 三、开始虚拟制片 效果 步骤 一、下载素材 首先下载绿幕视频素材 链接:百度网盘 请输入提取码 提取码:jyfk 二、将视频转成PNG序列 打开“Adobe Premiere Pro”,导入素材 …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
