算法笔记-第五章-质因子分解
算法笔记-第五章-质因子分解
- 小试牛刀
- 质因子2的个数
- 丑数
- 质因子分解
- 最小最大质因子
- 约数个数
小试牛刀
质因子2的个数
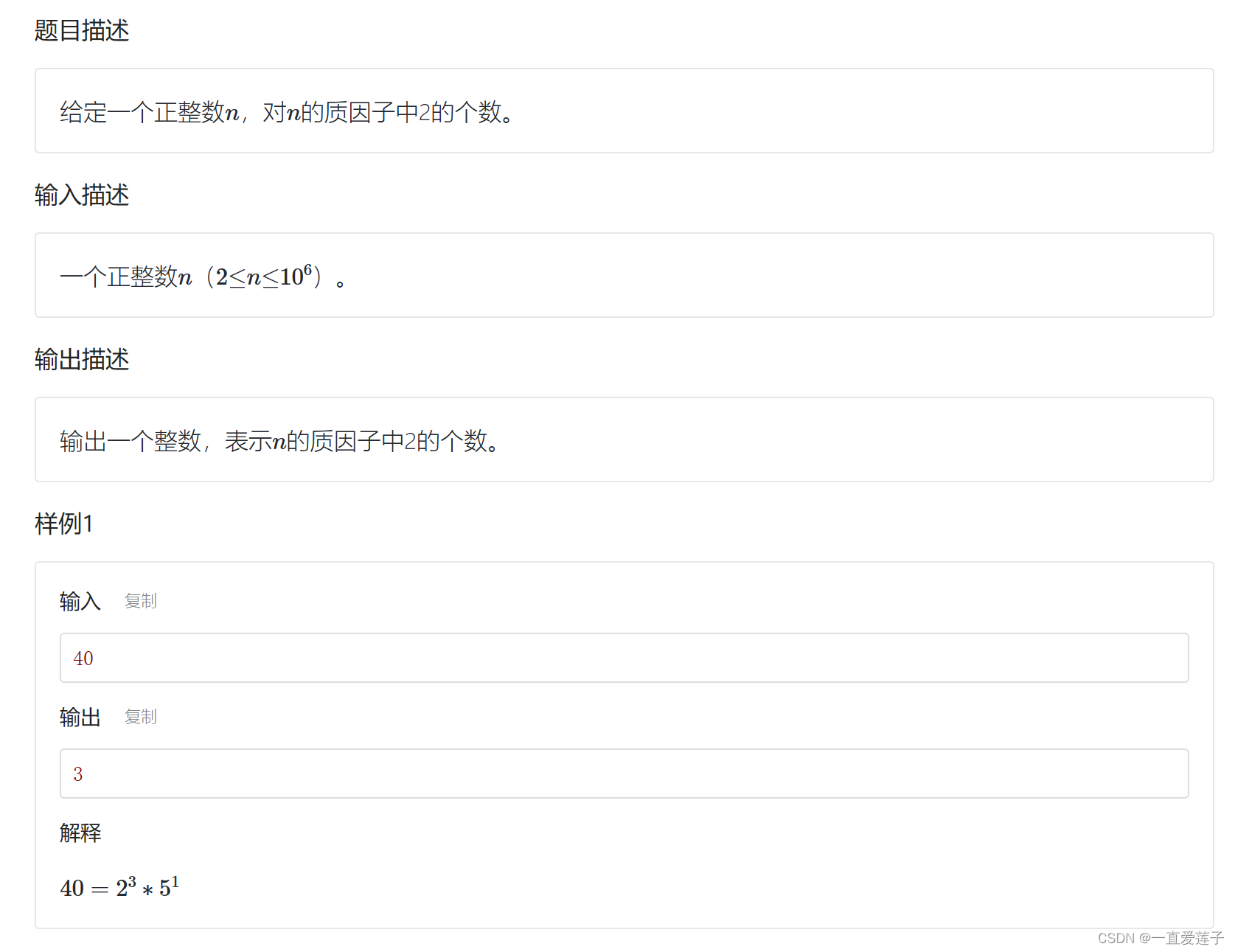
#include<cstdio>
int main()
{int n; scanf_s("%d", &n); int count = 0; while (n % 2 == 0) {count++; n /= 2; }printf("%d", count); return 0;
}
丑数
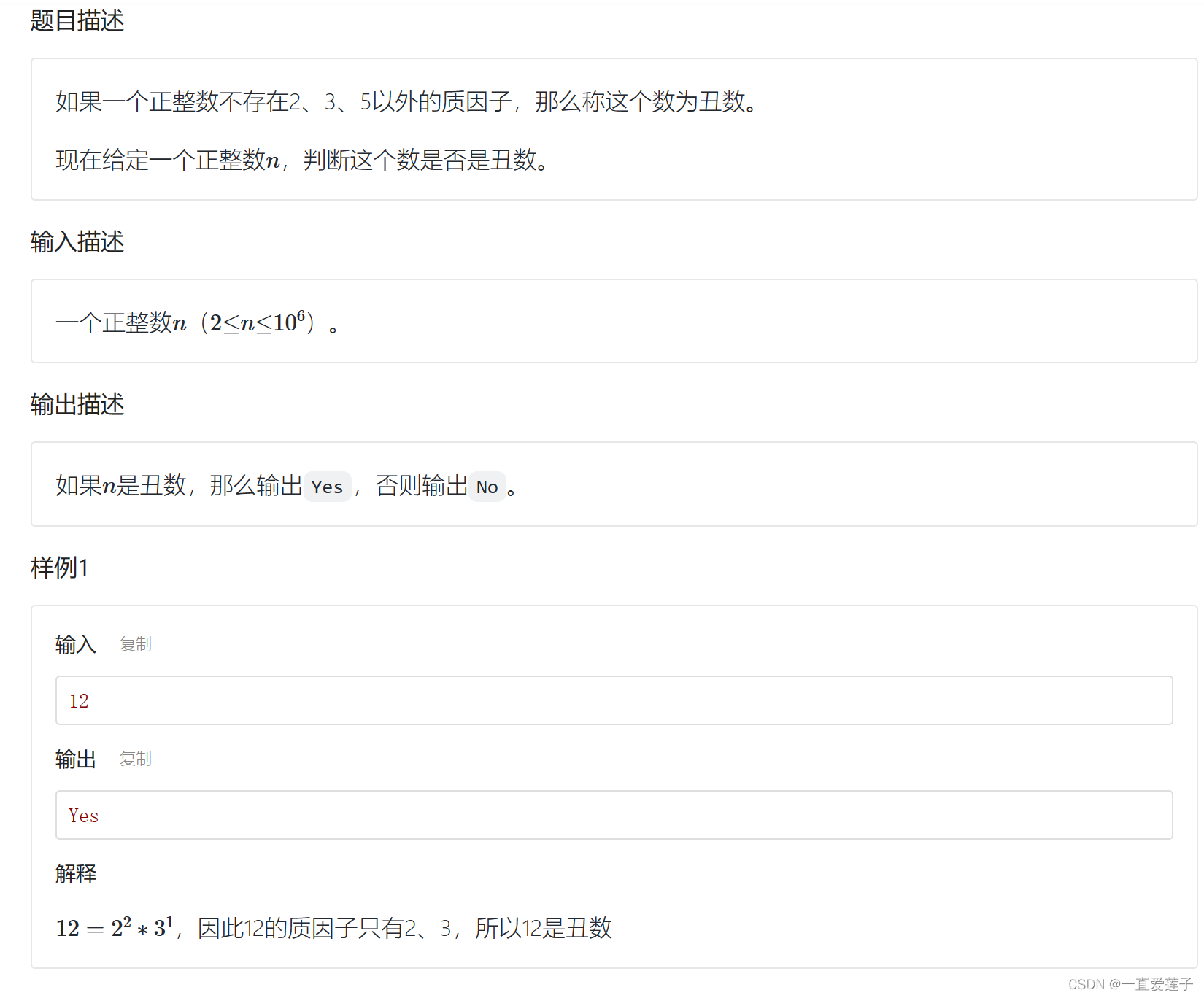

#include <cstdio>int main() {int n;scanf("%d", &n);while (n % 2 == 0) { n /= 2; }while (n % 3 == 0) { n /= 3; }while (n % 5 == 0) { n /= 5; }printf(n == 1 ? "Yes" : "No"); return 0;
}
质因子分解
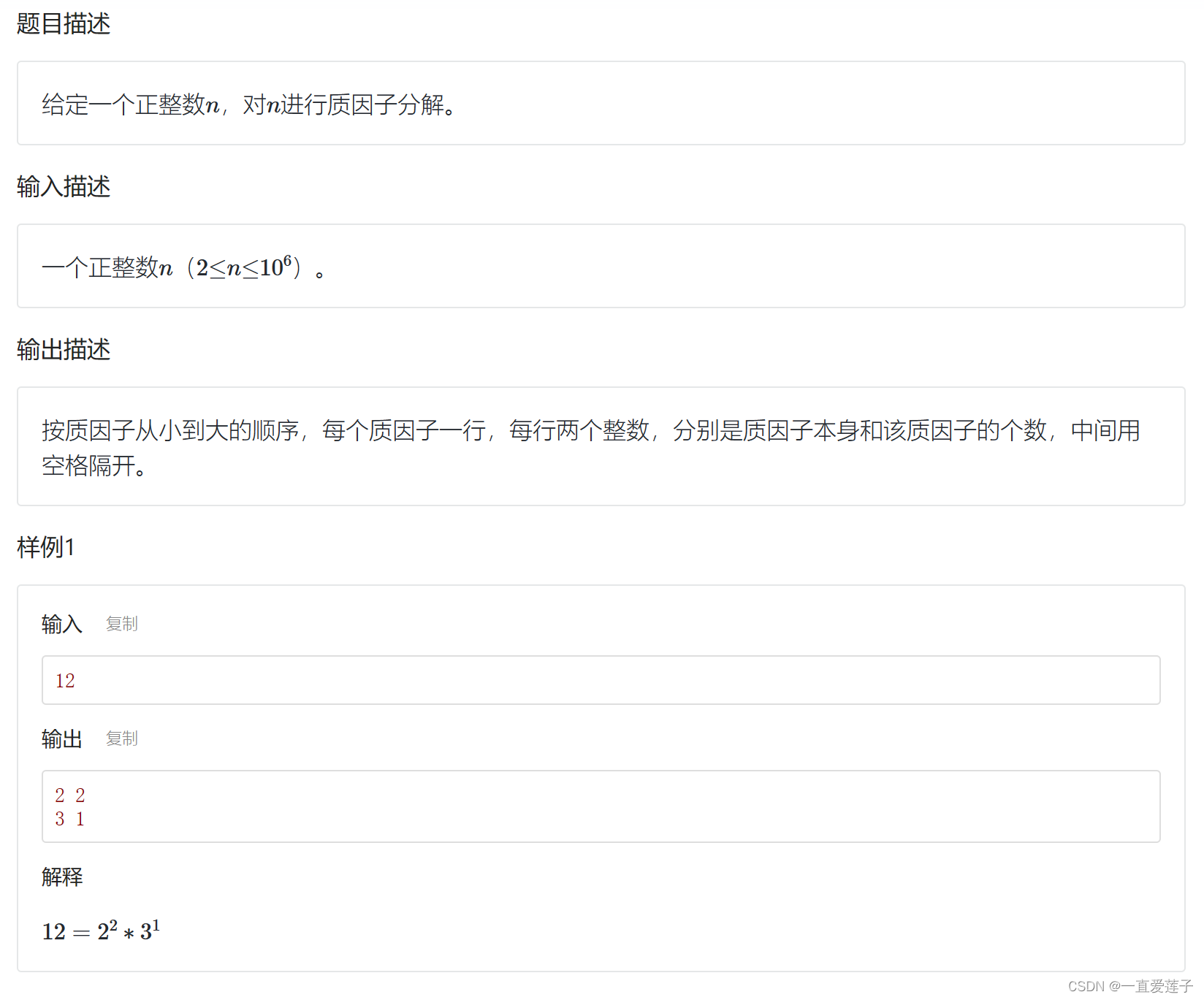
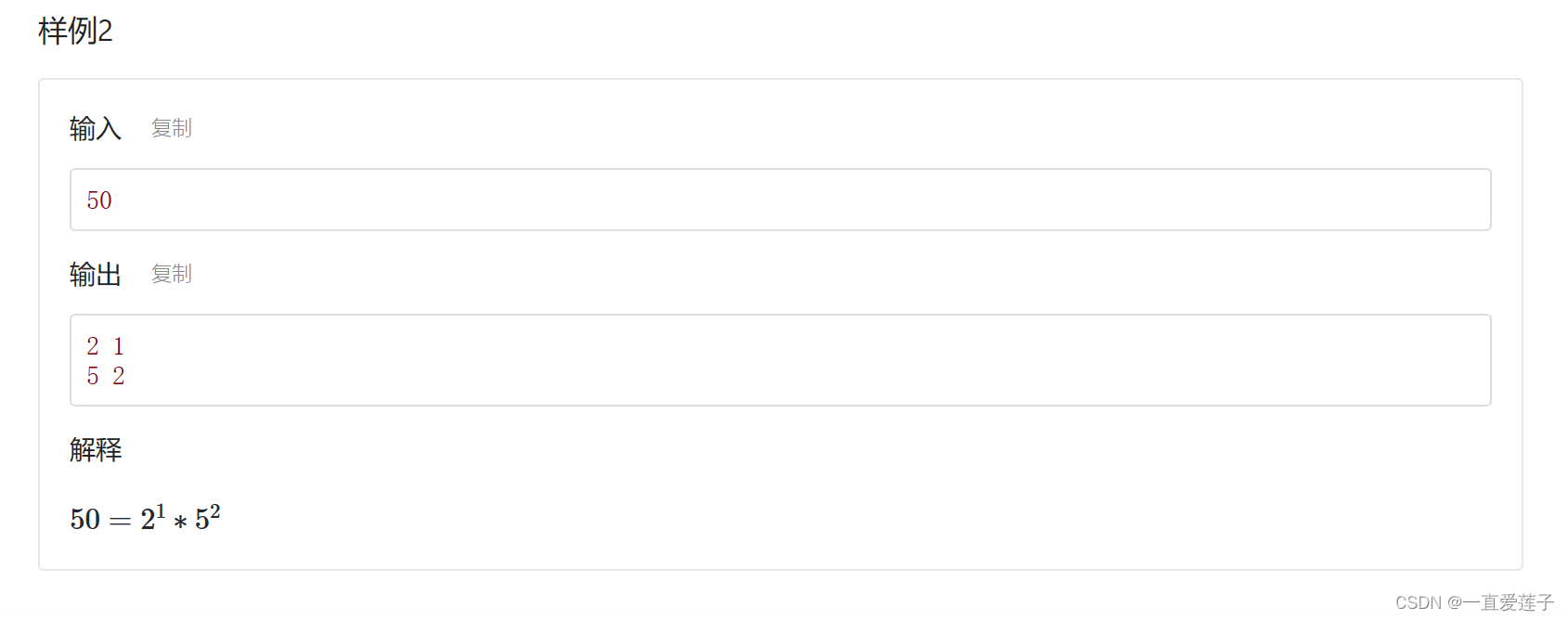
#include <cstdio>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;const int MAXN = 1000 + 1;
bool isPrime[MAXN];//布尔函数,用于指定可以为倍数的因子
vector<int> primes;//存储指定的倍数因子void getPrimes(int n)
{memset(isPrime, true, sizeof(isPrime));//对于布尔数组isprime进行复制truefor (int i = 2; i <= n; i++) //可以为倍数的从2开始到n(数的开方){if (isPrime[i]) //选取可以为倍数的因子{primes.push_back(i);//放到数组当中//并且下面对于访问过的倍数进行标记for (int j = i + i; j <= n; j += i) {isPrime[j] = false;}}}
}int main() {int n;scanf("%d", &n);getPrimes((int)sqrt(1.0 * n));//数的开方(带入到访问因子当中)for (int i = 0; i < primes.size() && n > 1; i++) //下面是进行因子判断和统计了{int counter = 0;//每一次都是统计每一个因子的数目while (n > 1 && n % primes[i] == 0) {counter++;n /= primes[i]; }if (counter > 0) //统计后进行输出数据 {printf("%d %d\n", primes[i], counter); }}if (n > 1) {printf("%d 1", n); }return 0;
}最小最大质因子
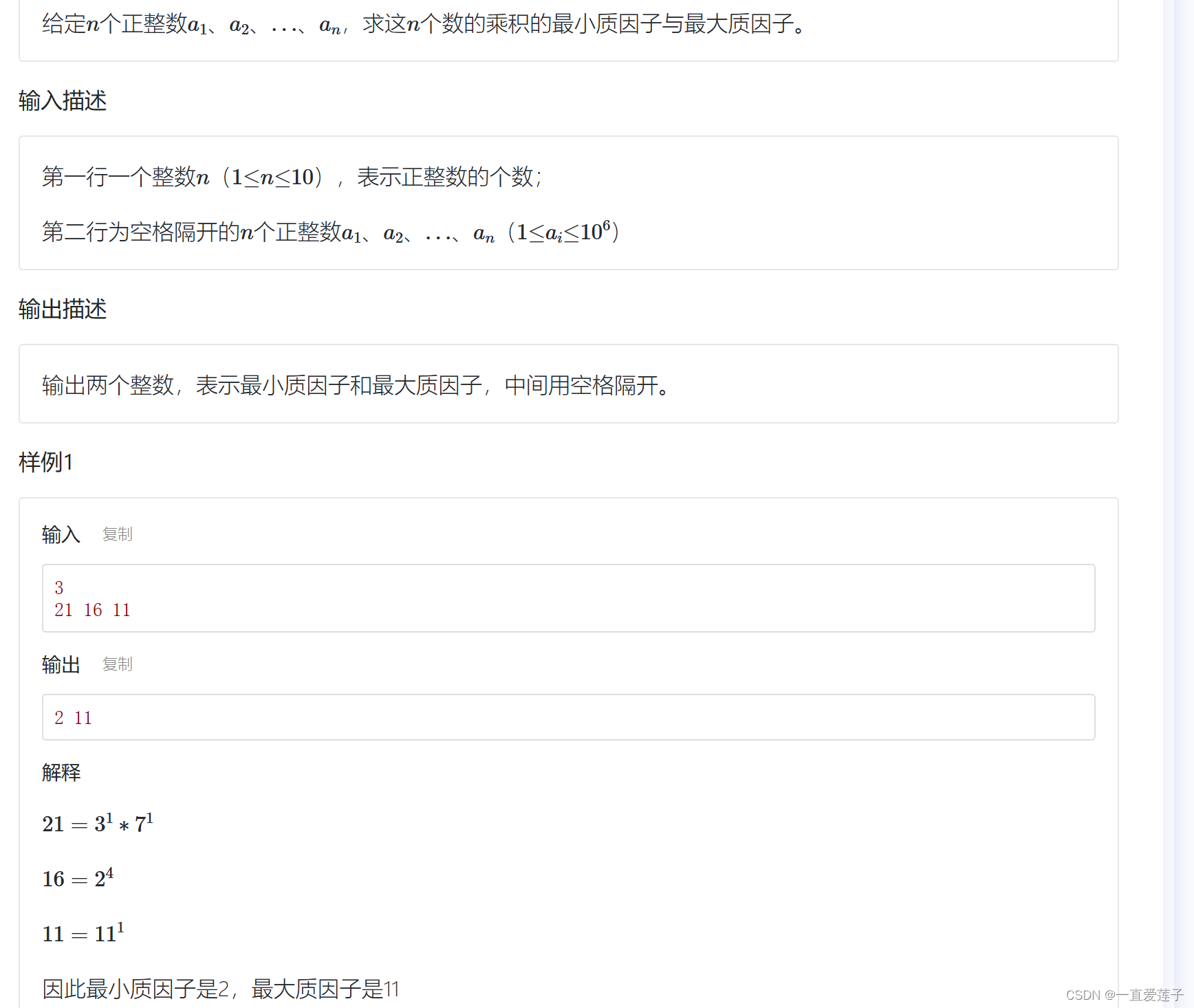
//最小最大质因子
#include <cstdio>
#include <cmath>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;const int INF = 0x3f;//表示无穷大数
const int MAXN = 1000 + 1;
bool isPrime[MAXN];
vector<int> primes;void getPrimes()
{memset(isPrime, true, sizeof(isPrime));//将布尔函数进行赋值for (int i = 2; i < MAXN; i++){if (isPrime[i]){primes.push_back(i);for (int j = i + i; j < MAXN; j += i) //将倍数因子进行标记{isPrime[j] = false;}}}
}int main()
{int n, x;scanf("%d", &n);getPrimes();//将倍数因子进行标记操作int minFactor = INF, maxFactor = 0;for (int i = 0; i < n; i++) {scanf("%d", &x);for (int j = 0; j < primes.size() && x > 1; j++) {int counter = 0; while (x > 1 && x % primes[j] == 0)//求得因子 {counter++;//统计因子数目 x /= primes[j]; }if (counter > 0) //取得因子最小值和因子最大值 {minFactor = min(minFactor, primes[j]); maxFactor = max(maxFactor, primes[j]); }}//最后条件:x除以prime[j]还有数且>1时候 if (x > 1) {minFactor = min(minFactor, x); maxFactor = max(maxFactor, x); }}printf("%d %d", minFactor, maxFactor); return 0;
}
约数个数

#include <cstdio>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;const int MAXN = 1000 + 1;
bool isPrime[MAXN];
vector<int> primes;void getPrimes(int n)
{memset(isPrime, true, sizeof(isPrime));for (int i = 2; i <= n; i++) {if (isPrime[i]) {primes.push_back(i);for (int j = i + i; j <= n; j += i){isPrime[j] = false;}}}
}int main() {int n;scanf("%d", &n);getPrimes((int)sqrt(1.0 * n));int result = 1;for (int i = 0; i < primes.size() && n > 1; i++) {int counter = 0;while (n > 1 && n % primes[i] == 0) {counter++;n /= primes[i];}if (counter > 0) {result = result * (counter + 1);}}if (n > 1) {result = result * 2;}printf("%d", result);return 0;
}
相关文章:

算法笔记-第五章-质因子分解
算法笔记-第五章-质因子分解 小试牛刀质因子2的个数丑数 质因子分解最小最大质因子约数个数 小试牛刀 质因子2的个数 #include<cstdio> int main() {int n; scanf_s("%d", &n); int count 0; while (n % 2 0) {count; n / 2; }printf("%…...
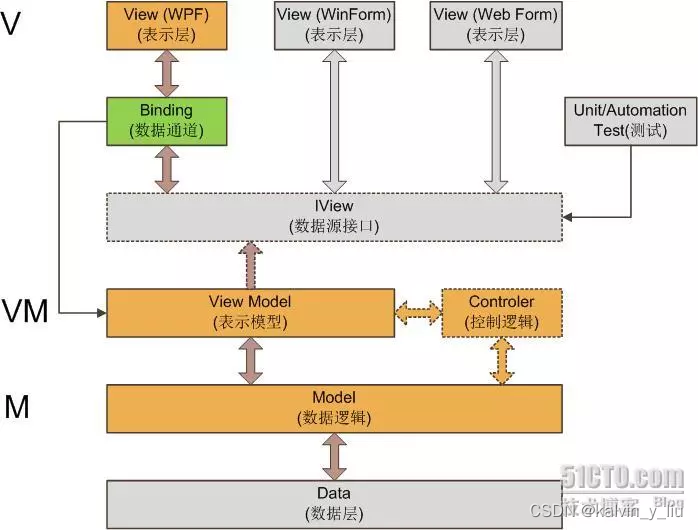
适用于WPF的设计模式
适用于WPF的设计模式 讨论“XAML能不能写逻辑代码”这个问题。我发现这是个有歧义的问题。这个问题可以有两种意思: XAML能不能用来写逻辑代码? XAML文件里能不能包含逻辑代码? 对于第一种意思——XAML是一种声明性语言,就是用来…...

C++与多态
多态的本质是允许对象以其实际类型的行为方式来操作,而不仅仅是其静态类型所声明的方式。 多态是面向对象编程中的一种核心概念,它允许对象根据其具体类型执行相应的操作,而不是其声明的类型。我们可以使用一个经典的动物的例子来说明这一点。…...
ios 对话框UIAlertController放 tableview
//强弱引用 #define kWeakSelf(type)__weak typeof(type)weak##type type; -(void) showUIAlertTable {kWeakSelf(self)UIAlertController *alert [UIAlertController alertControllerWithTitle:NSLocalizedString("select_stu", nil) message:nil prefer…...

警告:新版Outlook会向微软发送密码、邮件和其他数据
新的免费Outlook会将敏感数据发送给 Microsoft。 在没有通知或询问的情况下,Microsoft 授予自己对新 Outlook 用户的 IMAP 和 SMTP 访问数据的完全访问权限。也就是说,当用户设置 IMAP 帐户时,新的 Outlook 会将访问数据和服务器信息发送给 …...

数据结构C语言--基础实验
实验1 线性表的顺序实现 1.!顺序表的倒置 /**********************************/ /*文件名称:lab1-01.c */ /**********************************/ /*基于sequlist.h中定义的顺序表,编写算法函数reverse(sequence_list *L)&…...

wireshark抓包并进行Eigrp网络协议分析
路由协议 Eigrp EIGRP:Enhanced Interior Gateway Routing Protocol 即 增强内部网关路由协议。也翻译为 加强型内部网关路由协议。 EIGRP是Cisco公司的私有协议(2013年已经公有化)。 EIGRP结合了链路状态和距离矢量型路由选择协议的Cisco专用协议&a…...
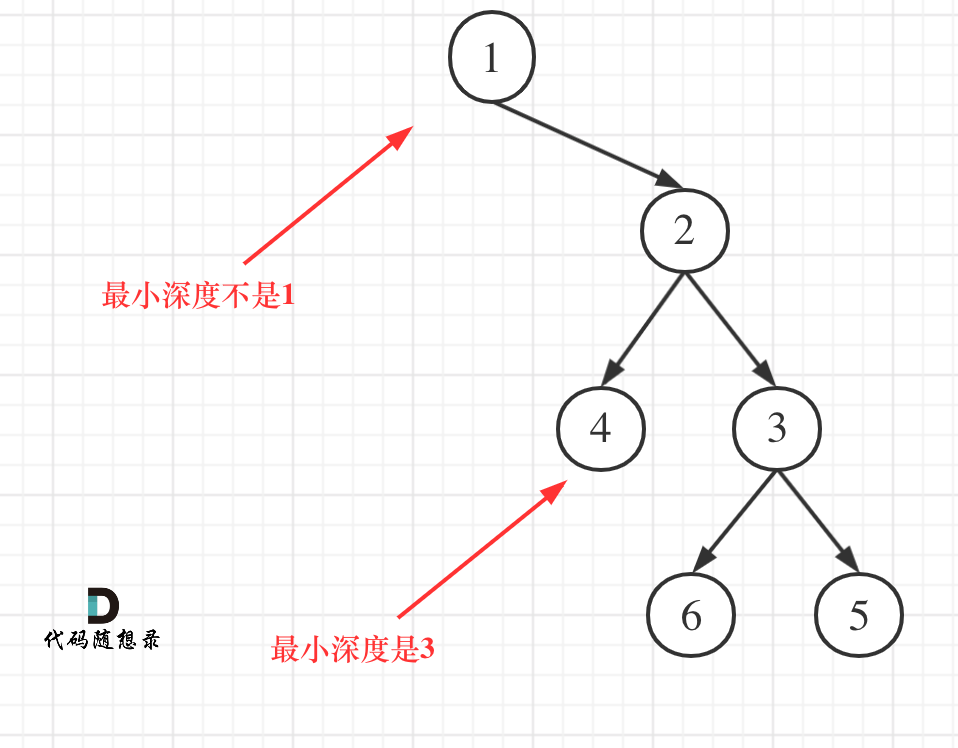
力扣刷题-二叉树-二叉树的层序遍历(相关题目总结)
思路 层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。 需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的…...

fundamental notes in 3D math
平面方程 a x b y c z d axbycz d axbyczd, 法向量 a , b , c a,b,c a,b,c, 点到平面的距离为 d / s q r t ( a 2 b 2 c 2 ) d / sqrt(a^2 b^2 c^2) d/sqrt(a2b2c2) , 距离可为正, 为负, 为正表示跟法向量方向一致, 为负表示相反 点 ( x o , y o , z o ) (x_o, y_o, z…...

【Java 进阶篇】JQuery DOM操作:舞动网页的属性魔法
在前端的舞台上,属性操作是我们与HTML元素进行互动的关键步骤之一。而JQuery,这位前端开发的巫师,通过简洁而强大的语法,为我们提供了便捷的属性操作工具。在这篇博客中,我们将深入研究JQuery DOM操作中的属性操作&…...
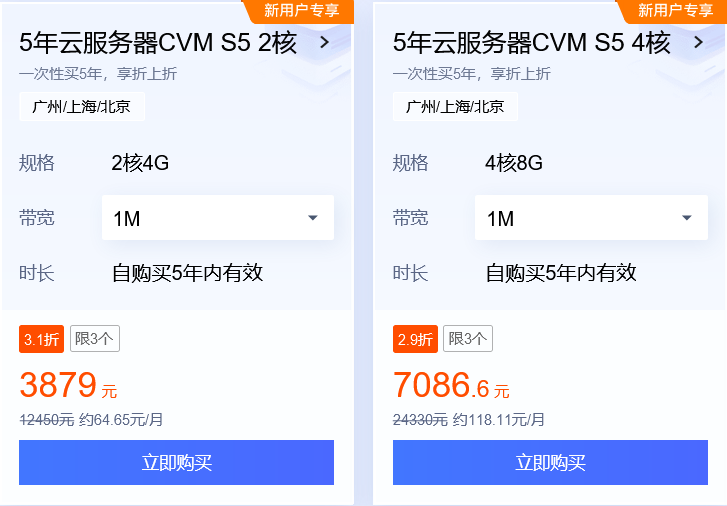
腾讯云5年云服务器还有吗?腾讯云5年时长服务器入口在哪?
如果你是一名企业家或者是一个热衷于数字化转型的创业者,那么腾讯云最近推出的一项优惠活动绝对不会让你无动于衷。现在,腾讯云正在大力推广一项5年特价云服务器活动,只需要花费3879元,你就可以享受到腾讯云提供的优质服务。 腾讯…...

odoo在iot领域的发展情况
Odoo 是一个全面的集成商业管理软件套装,主要提供企业资源规划 (ERP)、客户关系管理 (CRM)、电子商务、会计、库存管理等功能。在 IoT(物联网)领域,Odoo 侧重于通过提供一个中心化的平台来整合多方面的业务流程,包括生…...

Paas-云原生-容器-编排-持续部署
了解云原生 云原生架构让企业的基础设施,从简单的资源池化,转向以应用为中心,为应用赋能的敏捷、自运维、安全的云原生基础设施。以应用为中心的云原生基础设置,可以支持多种类型的应用,如微服务应用,中间件应用和AI 应用;可以提升应用交付效率,简化应用管理的复杂度;…...

sass 生成辅助色
背景 一个按钮往往有 4 个状态。 默认状态hover鼠标按下禁用状态 为了表示这 4 个状态,需要设置 4 个颜色来提示用户。 按钮类型一般有 5 个: 以 primary 类型按钮为例,设置它不同状态下的颜色: <button class"btn…...
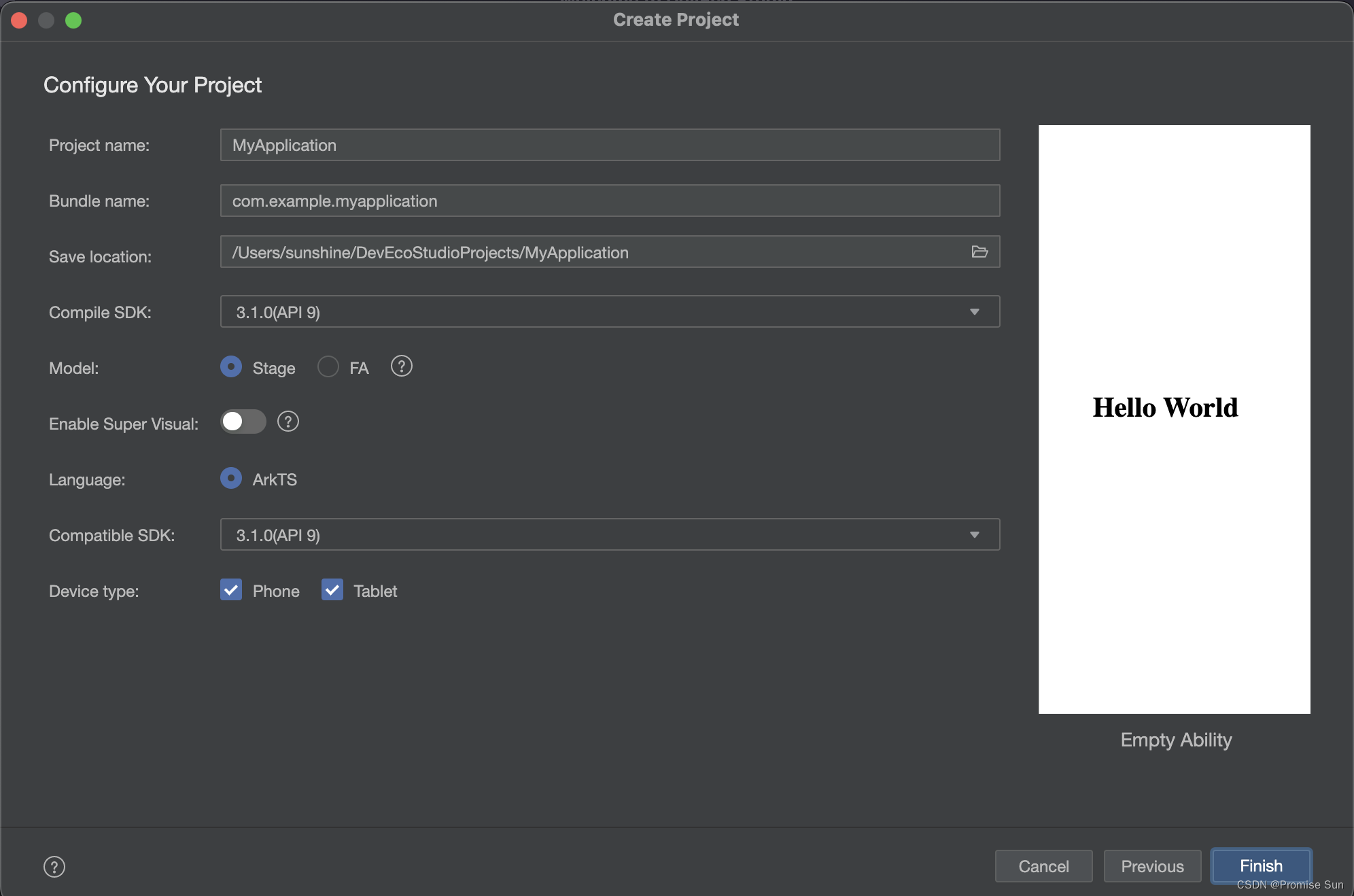
DevEco Studio开发工具下载、安装(HarmonyOS开发)_For Mac
一、说明 初学HarmonyOS开发,DevEco Studio开发工具的安装和使用是必须的。 (注:不多废话,跟着下面流程操作下载、安装DevEco Studio即可。) 二、下载DevEco Studio 1.官网下载地址: https://developer.…...
按键精灵中的字符串常用的场景
在使用按键精灵编写脚本时,与字符串有关的场景有以下几种: 1. 用时间字符串记录脚本使用截止使用时间 Dim localTime "2023-11-12 00:15:14" Dim networkTime GetNetworkTime() TracePrint networkTime If networkTime > localTime The…...

python数据结构与算法-01_抽象数据类型和面向对象编程
Python 一切皆对象 举个例子,在 python 中我们经常使用的 list l list() # 实例化一个 list 对象 l l.append(1) # 调用 l 的 append 方法 l.append(2) l.remove(1) print(len(l)) # 调用对象的 __len__ 方法在后面实现新的数据类型时,我们将…...

纯手写 模态框、消息弹框、呼吸灯
在有些做某些网页中,应用不想引用一些前端框架,对于一些比较常用的插件可以纯手写实现 1、模态框 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>Water Ripple Effect</title> <style…...

windows安装composer并更换国内镜像
第一步、官网下载 下载地址 Composer安装https://getcomposer.org/Composer-Setup.exe第二步、双击安装即可 第三步选择 php安装路径并配置path 第四步、 composer -v查看安装是否成功,出现成功界面 第五步、查看镜像地址并更换(composer国内可能较慢…...

c++ basic_string 和string区别
在C中,basic_string 是一个模板类,而 string 是 basic_string 的一个具体实例化,即 basic_string<char>。basic_string 模板类被设计为支持多种字符类型,而 string 是其中一种特定字符类型的字符串类。 具体来说࿰…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
