深入理解强化学习——多臂赌博机:梯度赌博机算法的数学证明
分类目录:《深入理解强化学习》总目录
通过将梯度赌博机算法理解为梯度上升的随机近似,我们可以深人了解这一算法的本质。在精确的梯度上升算法中,每一个动作的偏好函数 H t ( a ) H_t(a) Ht(a)与增量对性能的影响成正比:
H t + 1 ( a ) = H t ( a ) + α ∂ E [ R t ] ∂ H t ( a ) H_{t+1}(a)=H_t(a)+\alpha\frac{\partial E[R_t]}{\partial H_t(a)} Ht+1(a)=Ht(a)+α∂Ht(a)∂E[Rt]
这里性能的衡量指标定义为总体的期望收益:
E [ R t ] = ∑ x π t ( x ) q ∗ ( x ) E[R_t]=\sum_x\pi_t(x)q_*(x) E[Rt]=x∑πt(x)q∗(x)
而增量产生的影响就是上述性能衡量指标对动作偏好的偏导数。当然,我们不可能真的实现精确的梯度上升,因为真实的 q ∗ ( x ) q_*(x) q∗(x)是不知道的。但是事实上,前面的更新公式采用期望价值时是等价的,即随机梯度上升方法的一个实例。对这个关系的证明只需要用初等的微积分推导几步。首先,我们仔细分析一下精确的性能梯度的定义:
∂ E [ R t ] ∂ H t ( a ) = ∂ ∂ H t ( a ) ∑ x π t ( x ) q ∗ ( x ) = ∑ x q ∗ ( x ) ∂ π t ( x ) ∂ H t ( a ) = ∑ x ( q ∗ ( x ) − B t ) ∂ π t ( x ) ∂ H t ( a ) \begin{aligned} \frac{\partial E[R_t]}{\partial H_t(a)}&=\frac{\partial}{\partial H_t(a)}\sum_x\pi_t(x)q_*(x)\\ &=\sum_xq_*(x)\frac{\partial \pi_t(x)}{\partial H_t(a)}\\ &=\sum_x(q_*(x)-B_t)\frac{\partial \pi_t(x)}{\partial H_t(a)} \end{aligned} ∂Ht(a)∂E[Rt]=∂Ht(a)∂x∑πt(x)q∗(x)=x∑q∗(x)∂Ht(a)∂πt(x)=x∑(q∗(x)−Bt)∂Ht(a)∂πt(x)
其中, B t B_t Bt被称为“基准项”,可以是任何不依赖于 x x x的标量。我们可以把它加进来,因为所有动作的梯度加起来为0, ∑ x ∂ π t ( x ) ∂ H t ( a ) \sum_x\frac{\partial \pi_t(x)}{\partial H_t(a)} ∑x∂Ht(a)∂πt(x),即随着 H t ( a ) H_t(a) Ht(a)的变化,一些动作的概率会增加或者减少,但是这些变化的总和为0,因为概率之和必须是1。然后我们将求和公式中的每项都乘以 π t ( x ) π t ( x ) \frac{\pi_t(x)}{\pi_t(x)} πt(x)πt(x),等式保持不变:
∂ E [ R t ] ∂ H t ( a ) = ∑ x π t ( x ) ( q ∗ ( x ) − B t ) ∂ π t ( x ) ∂ H t ( a ) 1 π t ( x ) = E [ ( q ∗ ( A t ) − B t ) ∂ π t ( A t ) ∂ H t ( a ) 1 π t ( A t ) ] = E [ ( R t − R ˉ t ) ∂ π t ( A t ) ∂ H t ( a ) 1 π t ( A t ) ] = E [ ( R t − R ˉ t ) π t ( A t ) ( I ( a = A t ) − π t ( a ) ) 1 π t ( A t ) ] = E [ ( R t − R ˉ t ) ( I ( a = A t ) − π t ( a ) ) ] \begin{aligned} \frac{\partial E[R_t]}{\partial H_t(a)}&=\sum_x\pi_t(x)(q_*(x)-B_t)\frac{\partial \pi_t(x)}{\partial H_t(a)}\frac{1}{\pi_t(x)}\\ &=E[(q_*(A_t)-B_t)\frac{\partial \pi_t(A_t)}{\partial H_t(a)}\frac{1}{\pi_t(A_t)}]\\ &=E[(R_t-\bar{R}_t)\frac{\partial \pi_t(A_t)}{\partial H_t(a)}\frac{1}{\pi_t(A_t)}]\\ &=E[(R_t-\bar{R}_t)\pi_t(A_t)(\mathbb{I}(a=A_t)-\pi_t(a))\frac{1}{\pi_t(A_t)}]\\ &=E[(R_t-\bar{R}_t)(\mathbb{I}(a=A_t)-\pi_t(a))] \end{aligned} ∂Ht(a)∂E[Rt]=x∑πt(x)(q∗(x)−Bt)∂Ht(a)∂πt(x)πt(x)1=E[(q∗(At)−Bt)∂Ht(a)∂πt(At)πt(At)1]=E[(Rt−Rˉt)∂Ht(a)∂πt(At)πt(At)1]=E[(Rt−Rˉt)πt(At)(I(a=At)−πt(a))πt(At)1]=E[(Rt−Rˉt)(I(a=At)−πt(a))]
注意,上面的公式其实是一个“求期望"的式子:对随机变量所有可能的取值进行函数求和,然后乘以对应取值的概率。在上面我们选择 B t = R ˉ t B_t=\bar{R}_t Bt=Rˉt,并且将 R ˉ t \bar{R}_t Rˉt用 q ∗ ( A t ) q_*(A_t) q∗(At)代替。这个选择是可行的,因为 E [ R t ∣ A t ] = q ∗ ( A t ) E[R_t|A_t]=q_*(A_t) E[Rt∣At]=q∗(At),而且 R t R_t Rt在给定 A t A_t At的情况下与任何其他东西都不相关。很快我们就可以确定 ∂ π t ( x ) ∂ H t ( a ) = π t ( x ) ( I ( a = A t ) − π t ( a ) ) \frac{\partial \pi_t(x)}{\partial H_t(a)}=\pi_t(x)(\mathbb{I}(a=A_t)-\pi_t(a)) ∂Ht(a)∂πt(x)=πt(x)(I(a=At)−πt(a)),表示如果 a = x a=x a=x就取1,否则取0。回想一下,我们的计划是把性能指标的梯度写为某个东西的期望,这样我们就可以在每个时刻进行采样,然后再进行与采样样本成比例地更新。将公式 H t + 1 ( a ) = H t ( a ) + α ∂ E [ R t ] ∂ H t ( a ) H_{t+1}(a)=H_t(a)+\alpha\frac{\partial E[R_t]}{\partial H_t(a)} Ht+1(a)=Ht(a)+α∂Ht(a)∂E[Rt]中的性能指标的梯度用一个单独样本的期望值代替,可以得到:
H t + 1 ( a ) = H t ( a ) + α ( R t − R ˉ t ) ( I ( a = A t ) − π t ( a ) ) H_{t+1}(a)=H_t(a)+\alpha(R_t-\bar{R}_t)(\mathbb{I}(a=A_t)-\pi_t(a)) Ht+1(a)=Ht(a)+α(Rt−Rˉt)(I(a=At)−πt(a))
我们发现这和我们在文章《深入理解强化学习——多臂赌博机:梯度赌博机算法的基础知识》中给出的原始算法是一致的。现在我们只需要证明我们的假设 ∂ π t ( x ) ∂ H t ( a ) = π t ( x ) ( I ( a = A t ) − π t ( a ) ) \frac{\partial \pi_t(x)}{\partial H_t(a)}=\pi_t(x)(\mathbb{I}(a=A_t)-\pi_t(a)) ∂Ht(a)∂πt(x)=πt(x)(I(a=At)−πt(a))就可以了,在本文中就不详细阐述该假设的证明,但可以告诉大家这个假设是正确的。
上文我们已经证明了梯度赌博机算法的期望更新与期望收益的梯度是相等的,因此该算法是随机梯度上升算法的一种。这就保证了算法具有很强的收敛性。需要注意的的是,对于收益基准项,除了要求它不依赖于所选的动作之外,不需要其他任何的假设。例如,我们可以将其设置为0或1000,算法仍然是随机梯度上升算法的一个特例。基准项的选择不影响算法的预期更新,但它确实会影响更新值的方差,从而影响收敛速度。采用收益的平均值作为基准项可能不是最好的,但它很简单,并且在实践中很有效。
参考文献:
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习(第2版)[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践(原书第2版)[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL:强化学习教程 [M]. 人民邮电出版社, 2022
相关文章:

深入理解强化学习——多臂赌博机:梯度赌博机算法的数学证明
分类目录:《深入理解强化学习》总目录 通过将梯度赌博机算法理解为梯度上升的随机近似,我们可以深人了解这一算法的本质。在精确的梯度上升算法中,每一个动作的偏好函数 H t ( a ) H_t(a) Ht(a)与增量对性能的影响成正比: H t …...

StackExchange.Redis 高并发下timeout超时问题如何解决?
查看服务端程序负载还行,根据打印的连接看到一知半懂,按GitHub的issue提示,这2个Busy的数量不能比Min的大,即要提示Min的数值; 的各个字段: Timeout performing EXEC (1000ms): 表示在执行一个事务(MULTI..…...

JAVA基础7:数组
1.数组定义格式 1)数组概述 一次性声明大量的用于存储数据的变量 要存储的数据通常都是同类型数据,比如:考试成绩 数组(array)是一种用于存储多个相同类型数据的存储模型 2)数组定义格式 格式一:数据类…...
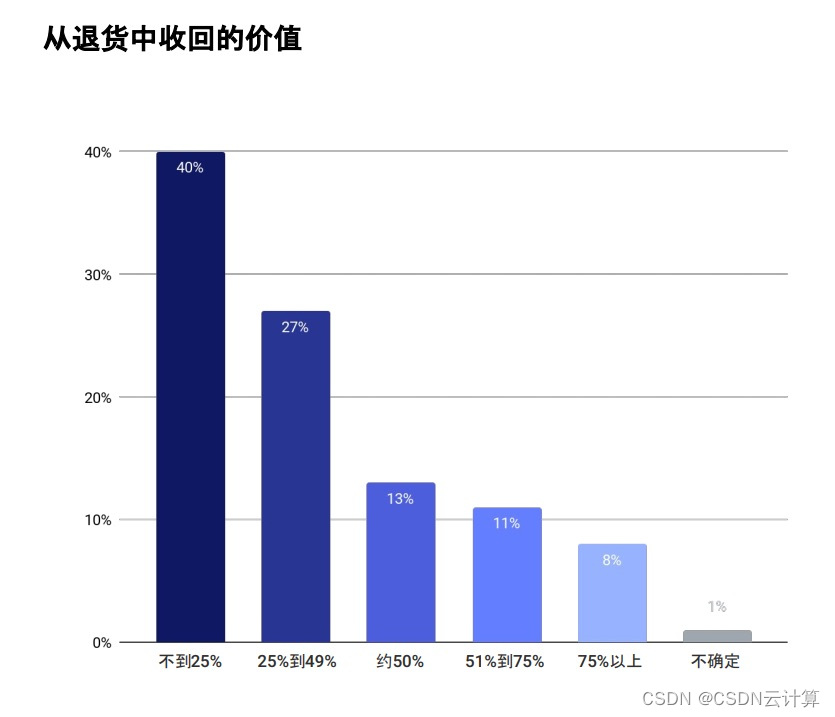
Riskified: 2023年电商政策滥用问题恶化,正严重挑战商家盈利底线
2023年11月14日,中国上海 —— 近日,由全球领先的电子商务欺诈和风险智能解决方案提供商 Riskified 发布的《政策滥用及其对商家的影响:2023年全球参考基准》报告显示,政策滥用问题正进一步恶化,超过九成电商商家正在承…...
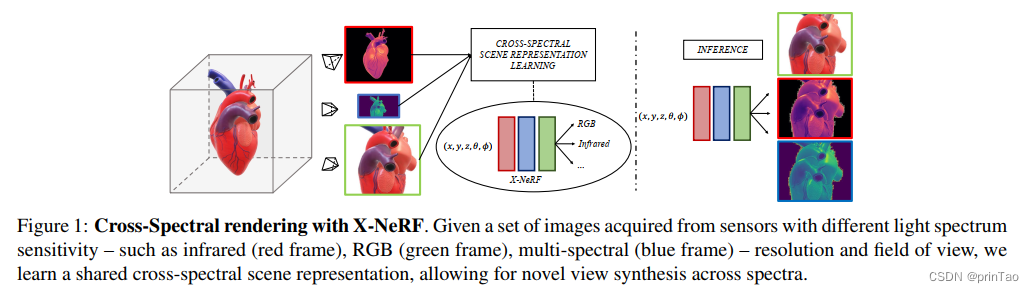
【论文阅读】多模态NeRF:Cross-Spectral Neural Radiance Fields
https://cvlab-unibo.github.io/xnerf-web intro 从不同的light spectrum sensitivity获取信息,同时需要obtain a unified Cross-Spectral scene representation – allowing for querying, for any single point, any of the information sensed across spectra。…...

Huggingface
1 介绍 Hugging Face 是一个开源模型社区。目前已经共享 300k 模型,100k 应用,50k 数据集(截至 231114 数据),可视为 AI 界的 github。 2 官网 https://huggingface.co/ 3 主要功能 3.1 Models 模型 大家都用过就…...

【深度学习】pytorch——常用工具模块
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~ 深度学习专栏链接: http://t.csdnimg.cn/dscW7 pytorch——常用工具模块 数据处理 torch.utils.data模块DatasetDataLoadersamplertorch.utils.data的使用 计算机视觉工具包 torchvisiontorchvision.d…...

【Android】统一系统动画
需求:除panel动画效果为弹出之外,其余的应用效果为渐入渐出 从系统层面统一把控动画效果,而不是单个应用自己处理 Android系统版本:9.0 代码地址 \frameworks\base\core\res\res\values\styles.xml 当时看注释,以为…...
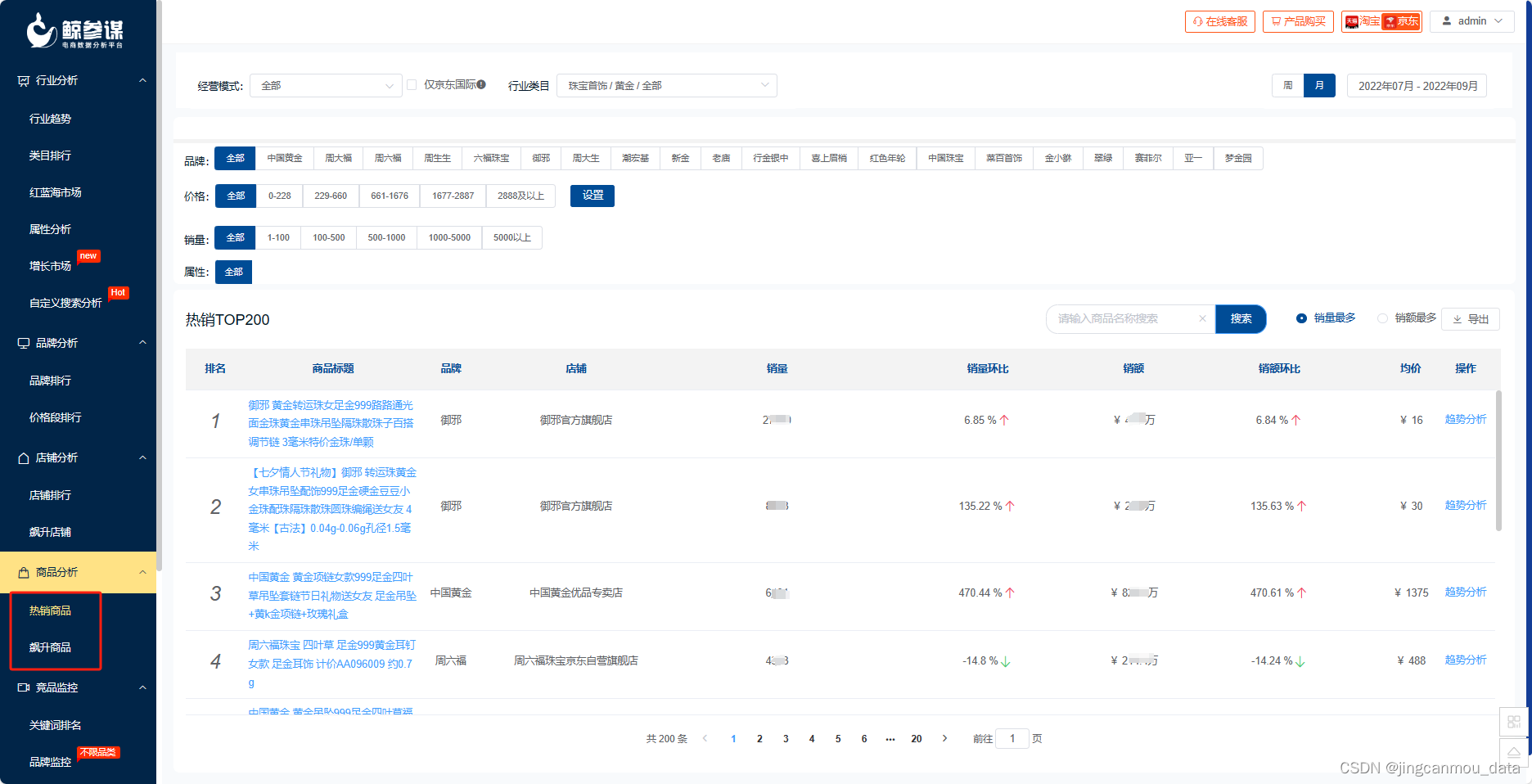
京东数据运营与分析:如何全面获取电商销售数据?
随着电商行业的快速发展,数据分析成为了电商运营中一个非常重要的环节,这一环往往能够帮助品牌方来提升销售业绩和管理效率。然而,如何获取到电商平台中详细、全面的销售数据是很多电商品牌方所关心的问题,事实上,第三…...

du_命令可以像find_命令那样列出最大的文件吗
【赠送】IT技术视频教程,白拿不谢!思科、华为、红帽、数据库、云计算等等_厦门微思网络的博客-CSDN博客文章浏览阅读418次。风和日丽,小微给你送福利~如果你是小微的老粉,这里有一份粉丝福利待领取...如果你是新粉关注到了小微&am…...

asp.net blazor集成TinyMCE.Blazor
asp.net blazor项目添加TinyMCE.Blazor nuget包 在blazor页面中添加,可以通过ScriptSrc参数配置自定义TinyMCE.Blazor js <EditForm class"mb-3" Model"Model" OnValidSubmit"HandleValidSubmit"><div class"form-gro…...
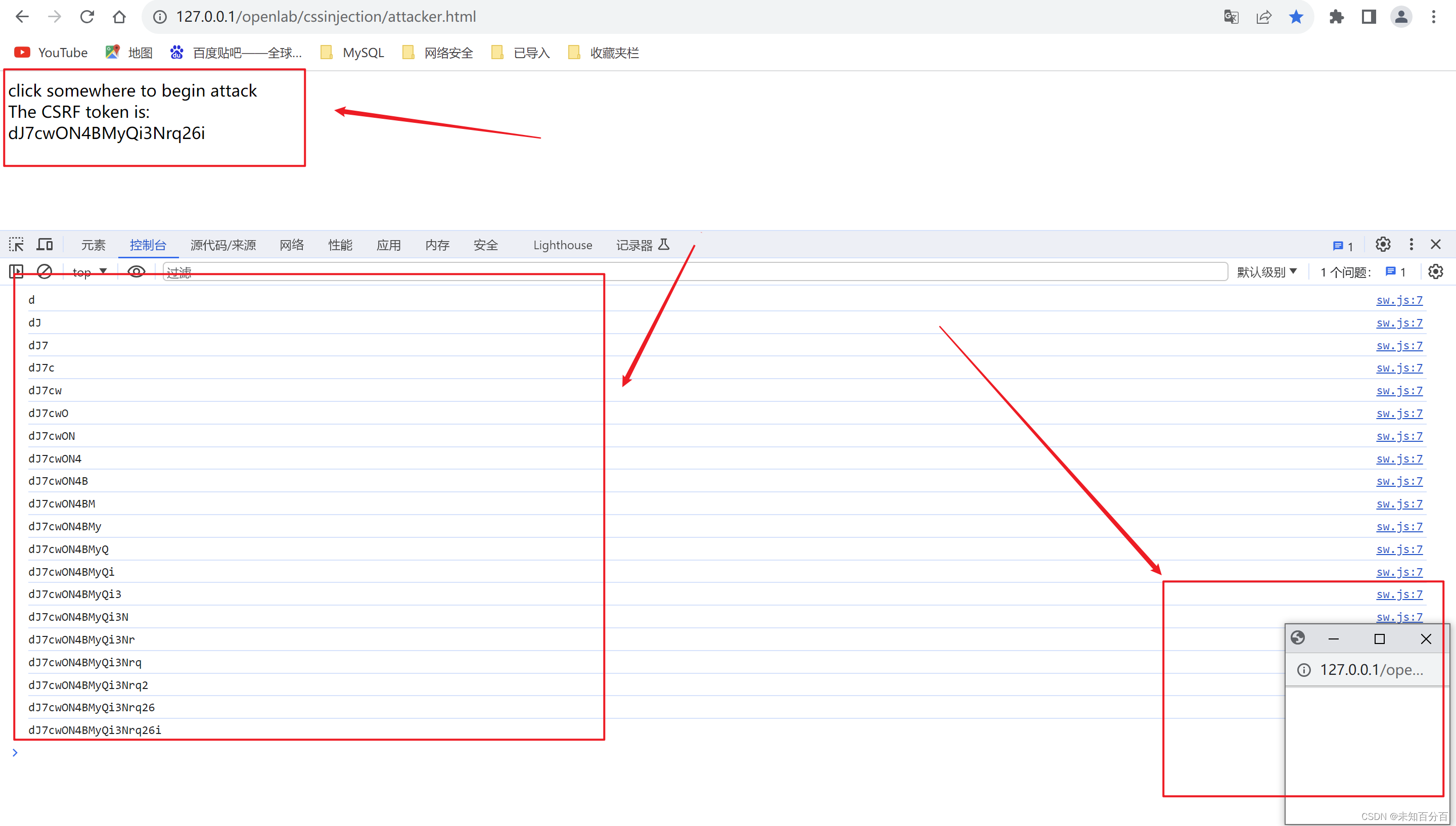
CSS注入的四种实现方式
目录 CSS注入窃取标签属性数据 简单的一个实验: 解决hidden 方法1:jsnode.js实现 侧信道攻击 方法2:对比波兰研究院的方案 使用兄弟选择器 方法3:jswebsocket实现CSS注入 实验实现: 方法4:window…...

突然消失的桌面文件如何恢复?详细教程让你轻松解决问题!
桌面文件突然消失,对于很多人来说,可能是个令人头疼的问题。这些文件可能包含重要的信息,也可能是数日甚至数周的努力成果。那么,当这种情况发生时,我们如何恢复丢失的文件呢?本文将提供一些实用的建议。 1…...

Springboot+Dubbo+Nacos 集成 Sentinel(入门)
Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。Sentinel 官网 1.版本选择 参考 SpringClou…...
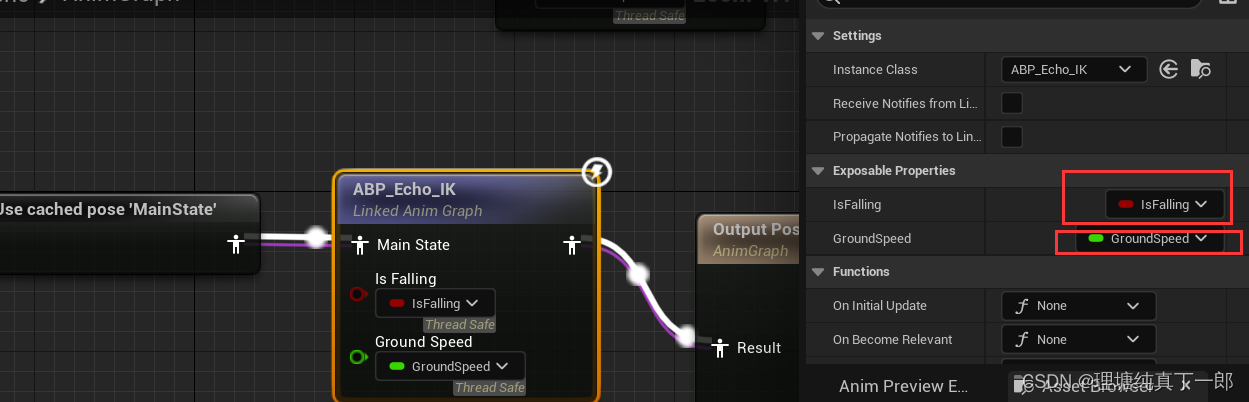
ARPG----C++学习记录05 Section10 武器类,IK重定向,装备和捡起武器,动画蓝图
代码更新 11.13 BAOfanTing/ARPG_Game_Code7ab54d2 GitHub 武器类 基于item类,创建一个weapon的C类,基于它创建一个蓝图,刀剑的网格体给它。在蓝图里调动之前在C写好的sin函数添加到世界偏移量里,得到一把悬浮刀 在item把重叠函…...
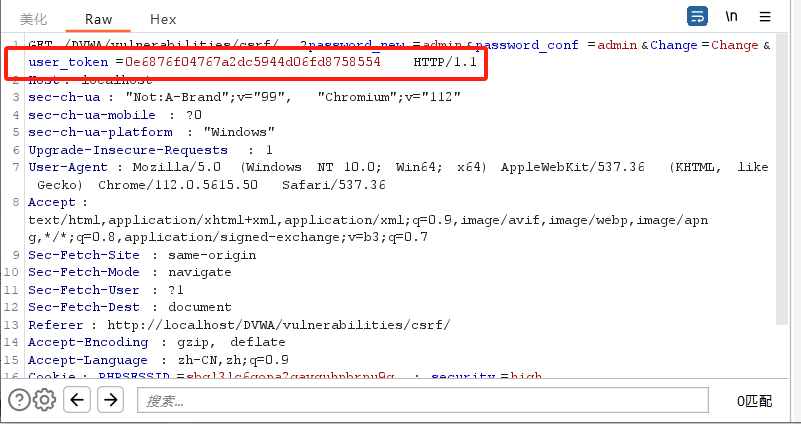
CSRF跨站请求伪造
CSRF CSRF(Cross-Site Request Forgery,跨站请求伪造)是通过诱导用户执行操作,利用用户在网站上的登录状态,以用户的身份在网站上执行恶意操作。 以下是CSRF攻击的一些关键特征: 用户身份:CSR…...

修改kernel驱动配置文件
对于内核分析,使用CONFIG_KPROBESy和CONFIG_KPROBE_EVENTSy来启用内核动态跟踪,而CONFIG_FRAME_POINTERy用于基于帧指针的内核堆栈。对于用户级分析,CONFIG_UPROBESy和CONFIG_UROBE_EVENTSy用于用户级动态跟踪。 添加位置在 kernel/.config...

采集摄像头数据的Golang应用
引言 如今,我们生活在一个信息爆炸的时代,数字化的发展给我们带来了无限的便利。在生活中,我们经常需要使用摄像头来进行图像采集,比如监控系统、人脸识别系统等。本文将介绍如何使用Golang语言来采集摄像头数据,并进…...
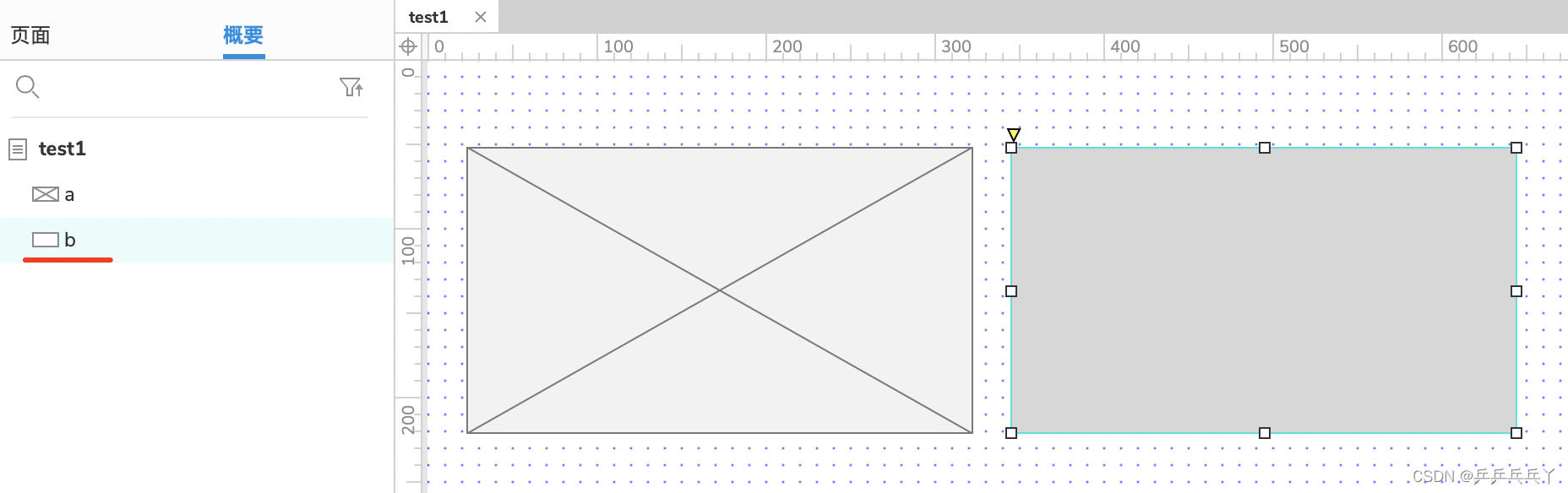
Axure9学习
产品经理零基础入门(四)Axure 原型图教程,2小时学会_哔哩哔哩_bilibili 1. ① 页面对应页面个数,概要对应每个页面的具体内容 ② 文件类型 ③ 备用间隔改为5分钟 ④ 当多个元件重叠,想把在下面的元件b直接拖出来&…...
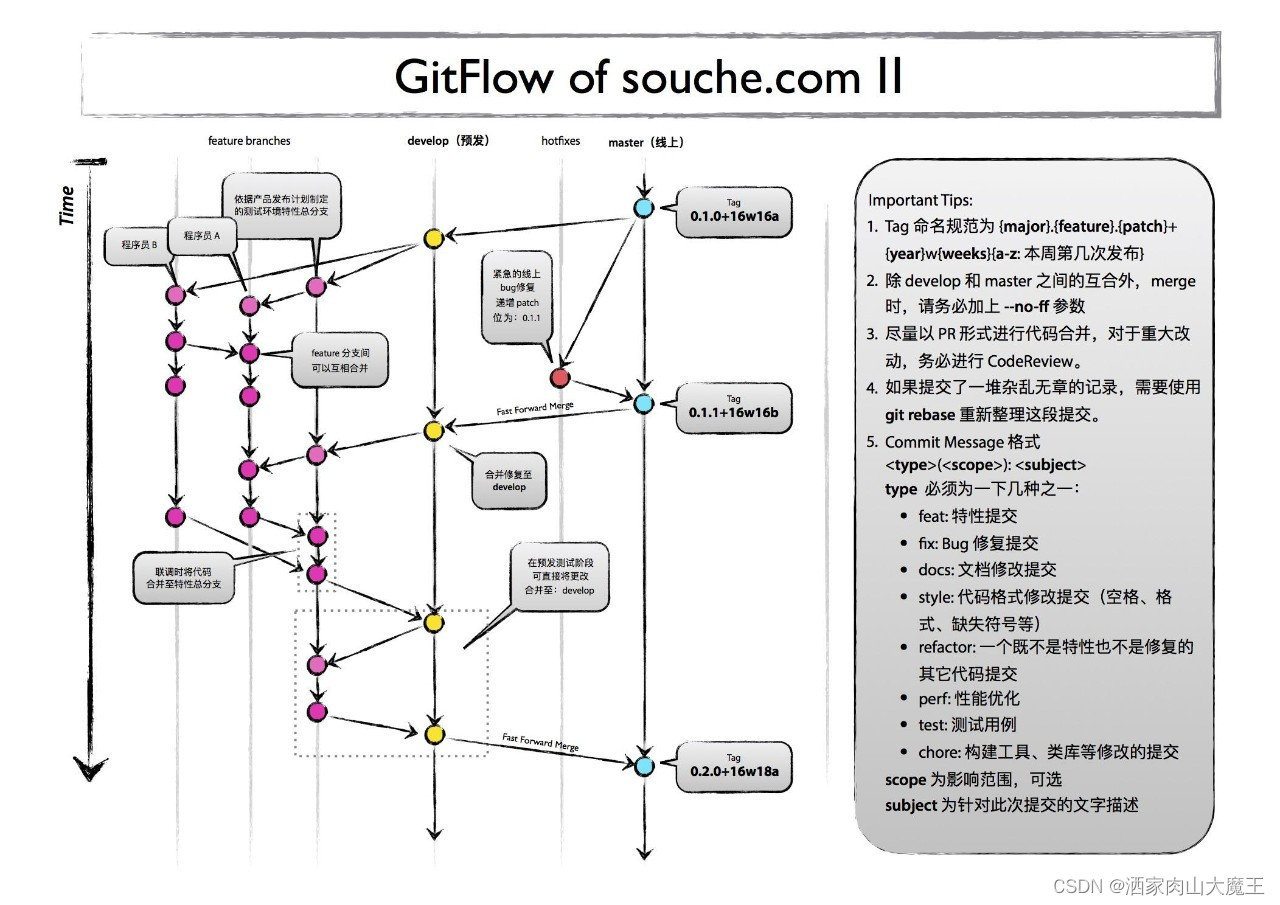
使用gitflow时如何合并hotfix
前言 在使用 git flow 流程时, 对于项目型的部署项目经常会遇到一个问题, 就是现场项目在使用历史版本时发现的一些问题需要修复, 但升级可能会有很大的风险或客户不愿意升级, 这时就要求基于历史版本进行 hotfix 修复. 基于历史发布版本的缺陷修复方式不同于最新发布版本的补…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
