AtCoder ABC154
C - Distinct or Not
签到题,注意大小写和以前的不一样
D - Dice in Line
签到题2,用个窗口即可
E - Almost Everywhere Zero
数位DP(搜索)的例题
pos表示当前搜索到的位置(开始为0,结束为n)
num表示已经使用的非0数字个数
cap表示搜索是否被限制,当之前搜索的数字比s小时cap=0,否则cap=1,开始时cap=1
# -*- coding: utf-8 -*-
# @time : 2023/6/2 13:30
# @file : atcoder.py
# @software : PyCharmimport bisect
import copy
import sys
from itertools import permutations
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(1000)def main():items = sys.version.split()if items[0] == '3.10.6':fp = open("in.txt")else:fp = sys.stdins = fp.readline().strip()n = len(s)k = int(fp.readline())@lru_cache(None)def get(pos, cap, num):if num == k:return 1if pos == n:return 0ret = 0si = int(s[pos])if cap == 0:ret += get(pos + 1, cap, num)ret += get(pos + 1, cap, num + 1) * 9else:if si == 0:ret += get(pos + 1, cap, num)else:ret += get(pos + 1, cap, num + 1)ret += get(pos + 1, 0, num + 1) * (si - 1)ret += get(pos + 1, 0, num)return retans = get(0, 1, 0)print(ans)if __name__ == "__main__":main()F - Many Many Paths
组合数学
显见
1.每个(r,c)点上的数都是一个组合数 C ( r + c , c ) C(r+c,c) C(r+c,c)
2.可以用容斥原理将ans拆成 g ( r 2 , c 2 ) − g ( r 2 , c 1 − 1 ) − g ( r 1 − 1 , c 2 ) + g ( r 1 − 1 , c 1 − 1 ) g(r_2,c_2)-g(r_2,c_1-1)-g(r_1-1,c_2)+g(r_1-1,c_1-1) g(r2,c2)−g(r2,c1−1)−g(r1−1,c2)+g(r1−1,c1−1)
其中 g g g函数是从(0,0)到(r,c)点的所有组合数的和。
将g按列分解(行也一样)
得到 g = C ( 0 , 0 ) + C ( 1 , 0 ) + . . . + C ( r , 0 ) + C ( 1 , 1 ) + C ( 2 , 1 ) + . . . + C ( r + 1 , 1 ) + . . . . C ( 1 + c , c ) + C ( 2 + c , c ) + . . . + C ( r + c , c ) g=C(0,0)+C(1,0)+...+C(r,0)+\\ C(1,1)+C(2,1)+...+C(r+1,1) + \\ ....\\ C(1+c,c)+C(2+c,c)+...+C(r+c,c) g=C(0,0)+C(1,0)+...+C(r,0)+C(1,1)+C(2,1)+...+C(r+1,1)+....C(1+c,c)+C(2+c,c)+...+C(r+c,c)
每一行都可以规约为 C ( r + c + 1 , c + 1 ) C(r+c+1, c+1) C(r+c+1,c+1)
这样可以写出一个 O ( n ) O(n) O(n)算法
# -*- coding: utf-8 -*-
# @time : 2023/6/2 13:30
# @file : atcoder.py
# @software : PyCharmimport bisect
import copy
import sys
from itertools import permutations
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(1000)def main():items = sys.version.split()if items[0] == '3.10.6':fp = open("in.txt")else:fp = sys.stdinr1, c1, r2, c2 = map(int, fp.readline().split())mod = 10 ** 9 + 7fac = [1] * 2000002iv = [1] * 2000002for i in range(1, 2000002):fac[i] = fac[i - 1] * i % moddef pw(a, x):if x == 1:return atemp = pw(a, x >> 1)if x & 1:return temp * temp * a % modelse:return temp * temp % modiv[1000001] = pw(fac[1000001], mod - 2)for i in range(1000000, -1, -1):iv[i] = (iv[i + 1] * (i + 1)) % moddef cmb(x, y):return fac[x] * iv[y] * iv[x - y] % moddef get(r, c):ret = 0for i in range(1, r + 2):ret = (ret + cmb(i + c, c)) % modreturn reta0, a1, a2, a3 = get(r2, c2), get(r1 - 1, c2), get(r2, c1 - 1), get(r1 - 1, c1 - 1)ans = (a0 - a1 - a2 + a3) % modprint(ans)if __name__ == "__main__":main()
相关文章:

AtCoder ABC154
C - Distinct or Not 签到题,注意大小写和以前的不一样 D - Dice in Line 签到题2,用个窗口即可 E - Almost Everywhere Zero 数位DP(搜索)的例题 pos表示当前搜索到的位置(开始为0,结束为n) …...

可以非常明显地感受到,一场有关直播带货的暗流正在涌动
虽然有关直播带货的争论依然还在持续,但是,我们依然无法否认今年的双十一依然是直播带货的高光时刻。无论是以淘宝、京东和拼多多为代表的传统电商平台,还是以抖音、快手为代表的新电商平台,几乎都将今年双十一的重心放在了直播带…...

C++中的四种构造函数
在C中,有几种不同类型的构造函数,基于它们的特性和用途,可以将它们分类为以下四种: 默认构造函数(Default Constructor): 如果没有为类定义任何构造函数,编译器将为其提供一个默认构造函数。这种…...

通过反射获取某个对象属性是否存在,并获取对象值
SneakyThrowspublic static void main(String[] args) {User user new User("张三", 10);// 获取指定属性名的值String propertyName "name2";Field[] fields user.getClass().getDeclaredFields();// 输出属性名Boolean flag false;for (Field field …...

【MySQL】存储过程与函数
一、存储过程 1、什么是存储过程 它是一组经过预先编译的SQL的封装它被存储在MySQL服务器上,当需要执行它时,客户端只需要向服务器发出调用命令,就可以把这一系列预先存储好的SQL语句全部执行 2、存储过程的优缺点 优点 简化操作…...

【数学】Pair of Topics—CF1324D
Pair of Topics—CF1324D 思路 很明显,需要对 a i a j > b i b j a_i a_j > b_i b_j aiaj>bibj 化简: a i − b i > b j − a j a_i - b_i > b_j - a_j ai−bi>bj−aj a i − b i > − ( a j − b j ) a_…...
Qt文档阅读笔记-Fetch More Example解析
Fetch More Example这个例子说明了如何在视图模型上添加记录。 这个例子由一个对话框组成,在Directory的输入框中,可输入路径信息。应用程序会载入路径信息的文件信息等。不需要按回车键就能搜索。 当有大量数据时,需要对视图模型进行批量增…...

QtC++与QTableView详解
介绍 QTableView 是 Qt 框架中用于显示表格数据的视图控件,它是 QAbstractItemView 类的子类。QTableView 通常与 QStandardItemModel 或者自定义的数据模型一起使用,用于展示二维表格型数据。以下是对 QTableView 的详细讲解和在 Qt 中的作用ÿ…...

HG/T 6002-2022 氟树脂粉末涂料检测
氟树脂粉末涂料是指以三氟氯乙烯-乙烯基醚、四氟乙烯-乙烯基醚等交联型氟树脂或聚偏二氟乙烯PVDF树脂为主要成膜物质,可加入颜料、填料、助剂、固化剂等制成的粉末涂料,主要用于铝型材、幕墙金属板、家电等表面的装饰和保护。 HG/T 6002-2022 氟树脂粉末…...

【java】idea可以连接但看不到database相关的files
问题 idea右侧有database工具栏,但点击没有在recent files看到数据库相关文件 问题排查 点击 help-> show log in explorer查看日志 发现显示 2023-11-13 10:28:09,694 [1244376] INFO - #c.i.c.ComponentStoreImpl - Saving appDebuggerSettings took 22…...

信驰达科技加入车联网联盟(CCC),推进数字钥匙发展与应用
CCC)的会员。 图 1 深圳信驰达正式成为车联网联盟(CCC)会员 车联网联盟(CCC)是一个跨行业组织,致力于推动智能手机与汽车连接解决方案的技术发展。CCC涵盖了全球汽车和智能手机行业的大部分企业,拥有150多家成员公司。CCC成员公司包括智能手机和汽车制造…...

p9 Eureka-搭建eureka服务
1.在user-service项目引入spring-cloud-starter-netflix-eureka-client的依赖 <dependencies><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></depen…...
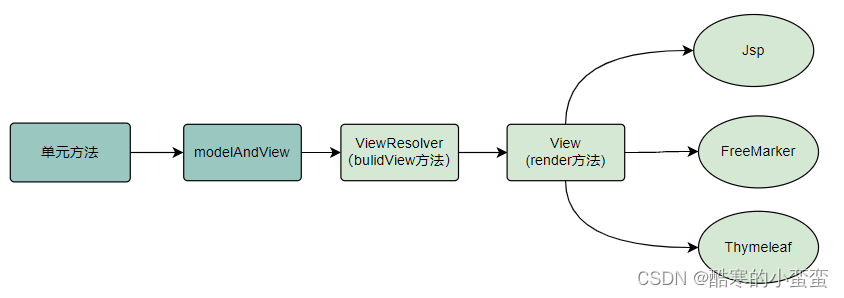
阶段七-Day01-SpringMVC
一、Sping MVC的介绍 1. 使用Front(前端)设计模式改写代码 1.1 目前我们的写法 目前我们所写的项目,持久层、业务层的类都放入到Spring容器之中了。他们之间需要注入非常方便,只需要通过Autowired注解即可。 但是由于Servlet整个生命周期都是被Tomca…...
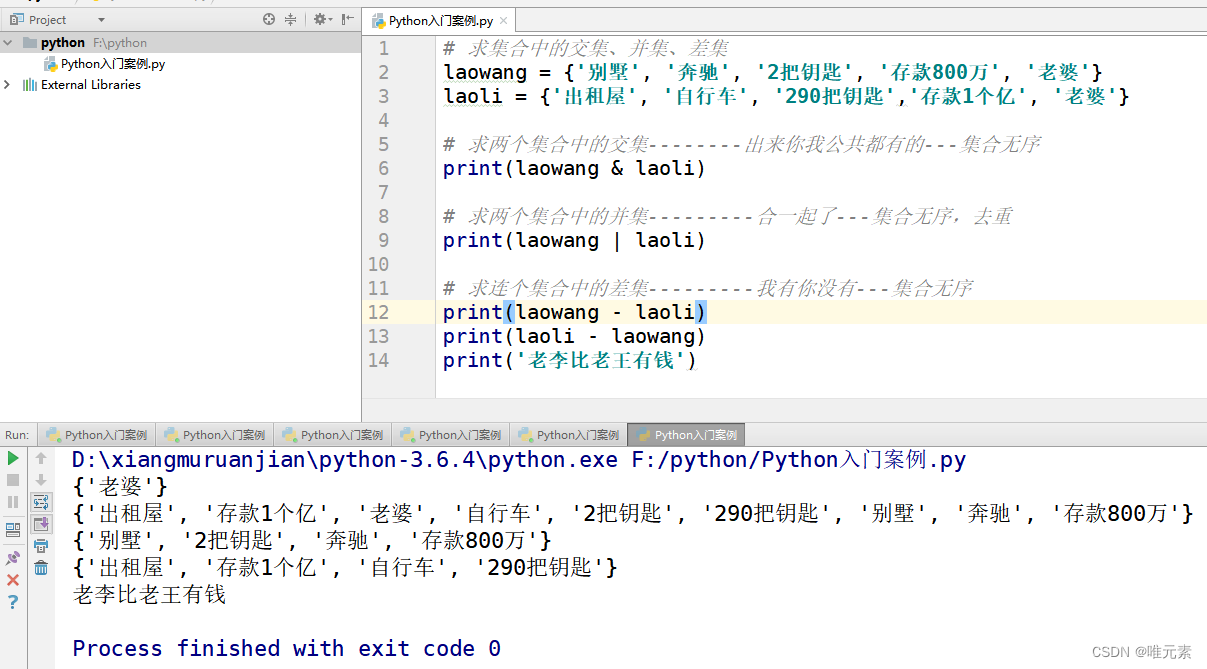
Python---集合中的交集 、并集 | 与差集 - 特性
用 & 来求两个集合的交集:-----键盘上的7上的符号,shift 7 同时按 用 | 来求两个集合的并集: -----键盘上的7上的符号,shift 同时按(就是enter键上面那个|\ ) 用 - 来求两个集合的差集ÿ…...

C++调用lua脚本,包括全局函数绑定、类绑定,十分钟快速掌握
系列文章目录 lua调用C/C的函数,十分钟快速掌握 C调用lua脚本,包括全局函数绑定、类绑定,十分钟快速掌握 系列文章目录摘要环境使用步骤码代码自定义函数多返回值变长参数 自定义类test_sol2.lua内容 程序输出 摘要 在这个快节奏的技术博客…...

快乐数[简单]
优质博文:IT-BLOG-CN 一、题目 编写一个算法来判断一个数n是不是快乐数。「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为1,也可能是无限循环但始终变不到1。如…...

Spring源码阅读-ClassPathXmlApplicationContext
第一步:new一个ClassPathXmlApplicationContext对象 ClassPathXmlApplicationContext xmlContext new ClassPathXmlApplicationContext("mylearn.xml"); 第二步:调用构造方法 public ClassPathXmlApplicationContext(String configLocatio…...

考研分享第2期 | 中央财经大学管理科学跨考北大软微金融科技406分经验分享
一、个人信息 本科院校:中央财经大学 管理科学与工程学院 管理科学专业 上岸院校:北京大学 软件与微电子学院 金融科技专业硕士 考试科目: 初试:思想政治理论 英语一 数学二 经济学综合 面试考察范围广,包括英语自…...

Linux安装java jdk配置环境 方便查询
编辑/etc/profile文件: vim /etc/profile 在文件尾部添加如下配置: export JAVA_HOME/usr/local/jdk1.8.0_161/ export CLASSPATH.: J A V A H O M E / j r e / l i b / r t . j a r : JAVA_HOME/jre/lib/rt.jar: JAVAHOME/jre/lib/rt.jar:JAVA_HOME/l…...

惊群效应之Nginx处理
文章目录 惊群概述Nginx 解决方案之锁的设计锁结构体原子锁创建原子锁获取原子锁实现原子锁释放 Nginx 解决方案之惊群效应总结: 惊群概述 在说nginx前,先来看看什么是“惊群”?简单说来,多线程/多进程(linux下线程进…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
