数据结构 | 图
最小生成树算法
Prime算法
算法思路:从已选顶点所关联的未选边中找出权重最小的边,并且生成树不存在环。
其中,已选顶点是构成最小生成树的结点,未选边是不属于生成树中的边。
例子:

第一步:
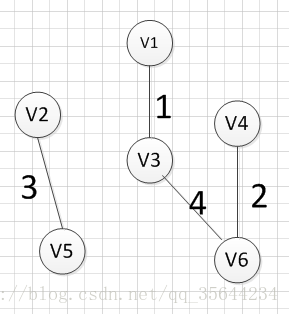
假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1:
第二步:

在v1,v3相关联的边中选一个权值最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—-v6=4

然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—-v4=2.

然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5

然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3

最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
Kruskal算法
算法思路:
(1)将边按权值从小到大的顺序添加到新图中,保证添加的过程中不会形成环(2)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
(3) n个顶点,n-1条边
例子 :
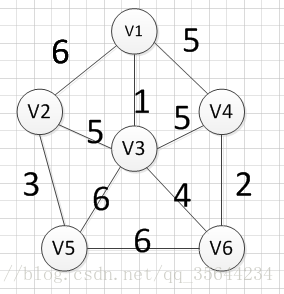
首先完整的图如下图:
然后,我们需要从这些边中找出权重最小的那条边,可以发现边(v1,v3)这条边的权重是最小的,所以我们输出边:v1—-v3=1
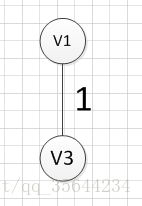
然后,我们需要在剩余的边中,再次寻找一条权重最小的边,可以发现边(v4,v6)这条边的权重最小,所以输出边:v4—v6=2
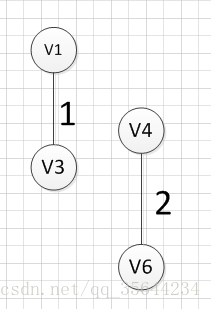
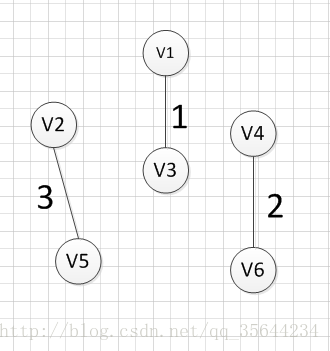
然后,我们再次从剩余边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以可以输出边:v2—-v5=3,
然后,我们使用同样的方式找出了权重最小的边:(v3,v6),所以我们输出边:v3—-v6=4
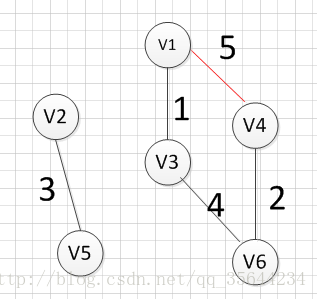
好了,现在我们还需要找出最后一条边就可以构造出一颗最小生成树,但是这个时候我们有三个选择:(v1,V4),(v2,v3),(v3,v4),这三条边的权重都是5,首先我们如果选(v1,v4)的话,得到的图如下:
我们发现,这肯定是不符合我们算法要求的,因为它出现了一个环,所以我们再使用第二个(v2,v3)试试,得到图形如下:
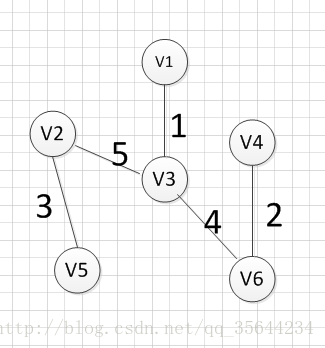
我们发现,这个图中没有环出现,而且把所有的顶点都加入到了这颗树上了,所以(v2,v3)就是我们所需要的边,所以最后一个输出的边就是:v2—-v3=5
拓扑排序
首先建立(n个顶点的)AOV网
(1) 在AOV网络中选一个没有直接前驱的顶点(入度为0的顶点),并输出之;
(2)从途中删去该顶点,同时删去所有它发出的边;
重复(1)和(2),直到全部顶点均已输出,拓扑有序序列形成,拓扑排序完成;
若图中还有未输出的顶点,但已跳出处理循环,这说明图中存在环;
AOV网络(Activity On VertexNetwork)
不能出现有向回路,即有向环。在AOV网络中如果出现了有向环,则意味着某项活动应以自己作为先决条件。
关键路径

最早最晚时间:
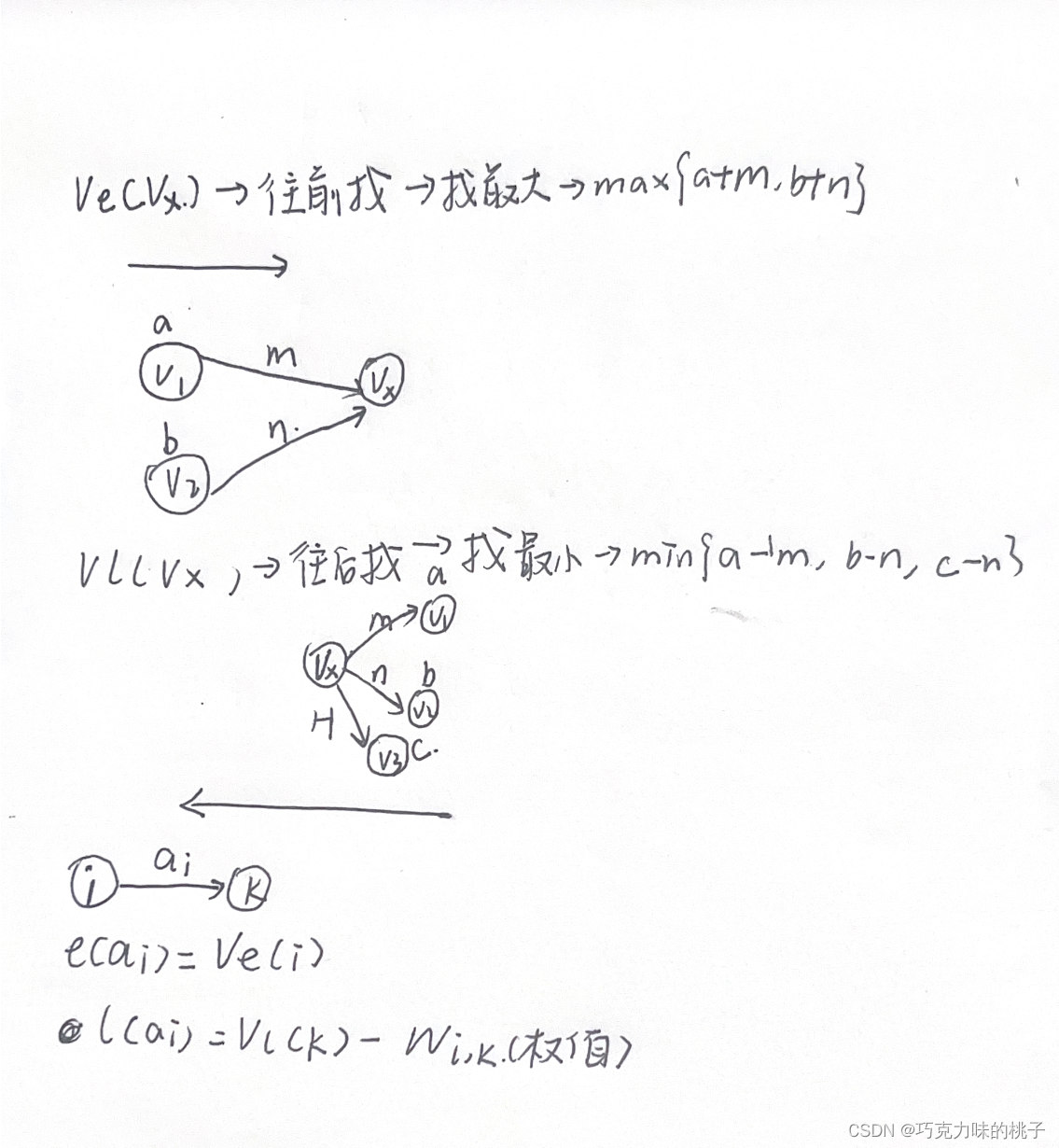
(1)事件vk的最早发生时间ve(k):决定了所有从vk开始的活动能够开工的最早时间;
(2)活动ai的最早开始时间e(i):指该活动弧的起点所表示的事件的最早发生时间;
(3)事件vk的最迟发生时间vl(k):指在不推迟整个工程完成的前提下,该事件最迟必须发生的时间;
若一个活动的时间余量为0,则说明该活动必须要如期完成,d(i)=0即l(i)=e(i)的活动ai是关键活动,由关键活动组成的路径就是关键路径。
步骤:
(1)求所有事件的最早发生时间ve();(2)求所有事件的最迟发生时间vl();
(3)求所有活动的最早发生事件e();
(4)求所有活动的最迟发生时间l();
(5)求所有活动的时间余量d();
(6)d(i)=0的就是关键活动,所有关键活动组成的路径即为关键路径。
ve(源点)等于0,vl(源点)需要自己算
ve(汇点)=vl(汇点) 需要自己算
相关文章:

数据结构 | 图
最小生成树算法 Prime算法 算法思路:从已选顶点所关联的未选边中找出权重最小的边,并且生成树不存在环。 其中,已选顶点是构成最小生成树的结点,未选边是不属于生成树中的边。 例子: 第一步: 假设我们从顶…...

[文件读取]shopxo 文件读取(CNVD-2021-15822)
1.1漏洞描述 漏洞编号CNVD-2021-15822漏洞类型文件读取漏洞等级⭐⭐漏洞环境VULFOCUS攻击方式 描述: ShopXO是一套开源的企业级开源电子商务系统。 ShopXO存在任意文件读取漏洞,攻击者可利用该漏洞获取敏感信息。 1.2漏洞等级 高危 1.3影响版本 ShopXO 1.4漏洞复现…...

zookeeper应用之分布式锁
在分布式系统中多个服务需要竞争同一个资源时就需要分布式锁,这里使用zookeeper的临时顺序节点来实现分布式锁。 在节点X下创建临时顺序节点,getChildren()获取节点X的所有子节点,判断当前节点是否是第一个子节点,如果是就获取锁…...

20. 机器学习——PCA 与 LDA
机器学习面试题汇总与解析——PCA 与 LDA 本章讲解知识点 什么是数据降维PCA本专栏适合于Python已经入门的学生或人士,有一定的编程基础。 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。 本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。这才是一…...

深度学习准召
准确率(Precision)和召回率(Recall)是两个用来评价一个模型的好坏的指标,它们有不同的意义: 准确率(Precision):准确率是在所有被模型判断为正例的样本中,有…...

AtCoder ABC154
C - Distinct or Not 签到题,注意大小写和以前的不一样 D - Dice in Line 签到题2,用个窗口即可 E - Almost Everywhere Zero 数位DP(搜索)的例题 pos表示当前搜索到的位置(开始为0,结束为n) …...

可以非常明显地感受到,一场有关直播带货的暗流正在涌动
虽然有关直播带货的争论依然还在持续,但是,我们依然无法否认今年的双十一依然是直播带货的高光时刻。无论是以淘宝、京东和拼多多为代表的传统电商平台,还是以抖音、快手为代表的新电商平台,几乎都将今年双十一的重心放在了直播带…...

C++中的四种构造函数
在C中,有几种不同类型的构造函数,基于它们的特性和用途,可以将它们分类为以下四种: 默认构造函数(Default Constructor): 如果没有为类定义任何构造函数,编译器将为其提供一个默认构造函数。这种…...

通过反射获取某个对象属性是否存在,并获取对象值
SneakyThrowspublic static void main(String[] args) {User user new User("张三", 10);// 获取指定属性名的值String propertyName "name2";Field[] fields user.getClass().getDeclaredFields();// 输出属性名Boolean flag false;for (Field field …...

【MySQL】存储过程与函数
一、存储过程 1、什么是存储过程 它是一组经过预先编译的SQL的封装它被存储在MySQL服务器上,当需要执行它时,客户端只需要向服务器发出调用命令,就可以把这一系列预先存储好的SQL语句全部执行 2、存储过程的优缺点 优点 简化操作…...

【数学】Pair of Topics—CF1324D
Pair of Topics—CF1324D 思路 很明显,需要对 a i a j > b i b j a_i a_j > b_i b_j aiaj>bibj 化简: a i − b i > b j − a j a_i - b_i > b_j - a_j ai−bi>bj−aj a i − b i > − ( a j − b j ) a_…...
Qt文档阅读笔记-Fetch More Example解析
Fetch More Example这个例子说明了如何在视图模型上添加记录。 这个例子由一个对话框组成,在Directory的输入框中,可输入路径信息。应用程序会载入路径信息的文件信息等。不需要按回车键就能搜索。 当有大量数据时,需要对视图模型进行批量增…...

QtC++与QTableView详解
介绍 QTableView 是 Qt 框架中用于显示表格数据的视图控件,它是 QAbstractItemView 类的子类。QTableView 通常与 QStandardItemModel 或者自定义的数据模型一起使用,用于展示二维表格型数据。以下是对 QTableView 的详细讲解和在 Qt 中的作用ÿ…...

HG/T 6002-2022 氟树脂粉末涂料检测
氟树脂粉末涂料是指以三氟氯乙烯-乙烯基醚、四氟乙烯-乙烯基醚等交联型氟树脂或聚偏二氟乙烯PVDF树脂为主要成膜物质,可加入颜料、填料、助剂、固化剂等制成的粉末涂料,主要用于铝型材、幕墙金属板、家电等表面的装饰和保护。 HG/T 6002-2022 氟树脂粉末…...

【java】idea可以连接但看不到database相关的files
问题 idea右侧有database工具栏,但点击没有在recent files看到数据库相关文件 问题排查 点击 help-> show log in explorer查看日志 发现显示 2023-11-13 10:28:09,694 [1244376] INFO - #c.i.c.ComponentStoreImpl - Saving appDebuggerSettings took 22…...

信驰达科技加入车联网联盟(CCC),推进数字钥匙发展与应用
CCC)的会员。 图 1 深圳信驰达正式成为车联网联盟(CCC)会员 车联网联盟(CCC)是一个跨行业组织,致力于推动智能手机与汽车连接解决方案的技术发展。CCC涵盖了全球汽车和智能手机行业的大部分企业,拥有150多家成员公司。CCC成员公司包括智能手机和汽车制造…...

p9 Eureka-搭建eureka服务
1.在user-service项目引入spring-cloud-starter-netflix-eureka-client的依赖 <dependencies><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></depen…...
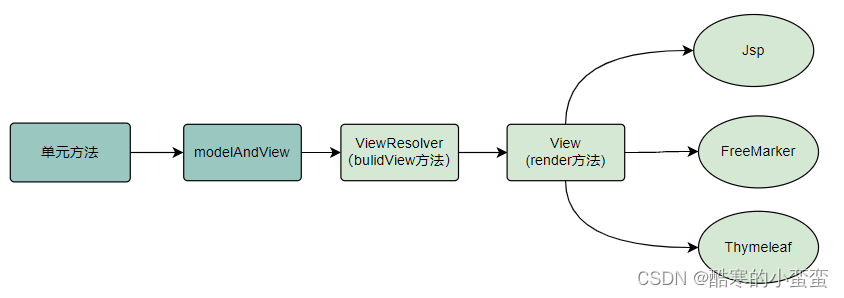
阶段七-Day01-SpringMVC
一、Sping MVC的介绍 1. 使用Front(前端)设计模式改写代码 1.1 目前我们的写法 目前我们所写的项目,持久层、业务层的类都放入到Spring容器之中了。他们之间需要注入非常方便,只需要通过Autowired注解即可。 但是由于Servlet整个生命周期都是被Tomca…...
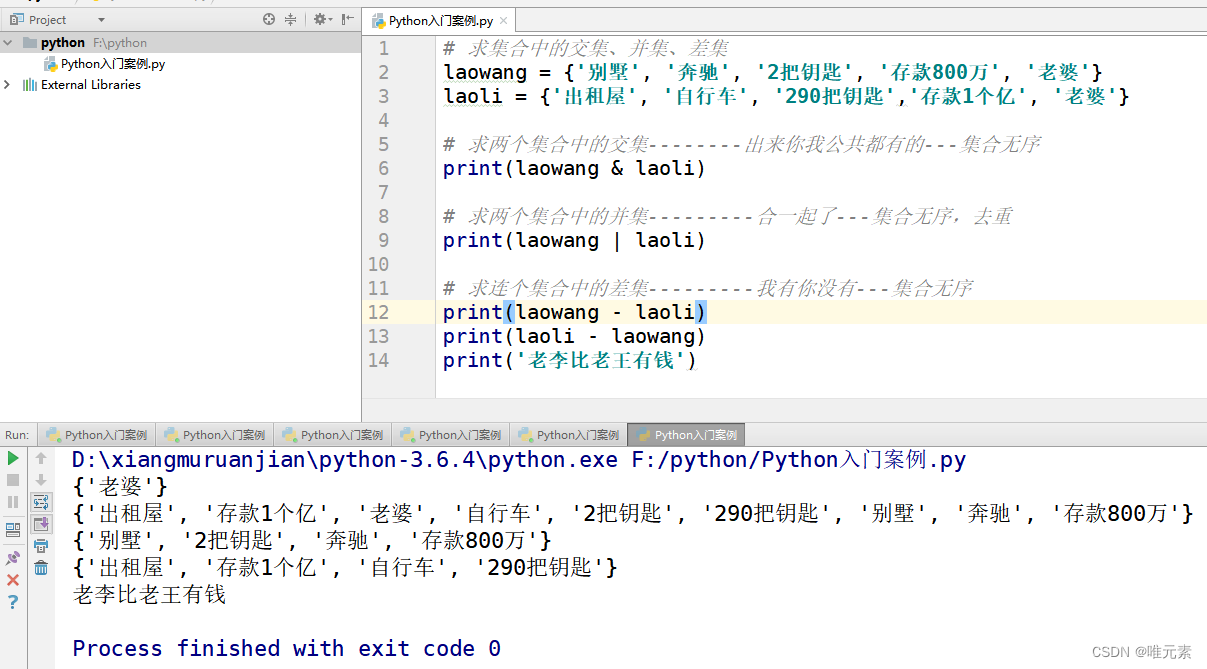
Python---集合中的交集 、并集 | 与差集 - 特性
用 & 来求两个集合的交集:-----键盘上的7上的符号,shift 7 同时按 用 | 来求两个集合的并集: -----键盘上的7上的符号,shift 同时按(就是enter键上面那个|\ ) 用 - 来求两个集合的差集ÿ…...

C++调用lua脚本,包括全局函数绑定、类绑定,十分钟快速掌握
系列文章目录 lua调用C/C的函数,十分钟快速掌握 C调用lua脚本,包括全局函数绑定、类绑定,十分钟快速掌握 系列文章目录摘要环境使用步骤码代码自定义函数多返回值变长参数 自定义类test_sol2.lua内容 程序输出 摘要 在这个快节奏的技术博客…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...