C++ RBTree 理论
目录
这个性质可以总结为
红黑树的最短最长路径
红黑树的路径范围
code
结构
搞颜色
类
插入
插入逻辑
新插入节点
思考:2. 检测新节点插入后,红黑树的性质是否造到破坏?
解决方法
变色
旋转+变色
第三种情况,如果根节点上面还有节点


这个性质可以总结为
1.每个节点不是红色就是黑色
2.根节点是黑色的
3.不能有两个连续的红色节点 ,即可以出现 红黑 黑黑 不能出现红红
4.每条路径上的黑色机节点数量不一样
至于性质5:每个叶子结点都是黑色的,这里的叶子节点并不是真的叶子节点,而是NIL节点,即空节点。如图(a):
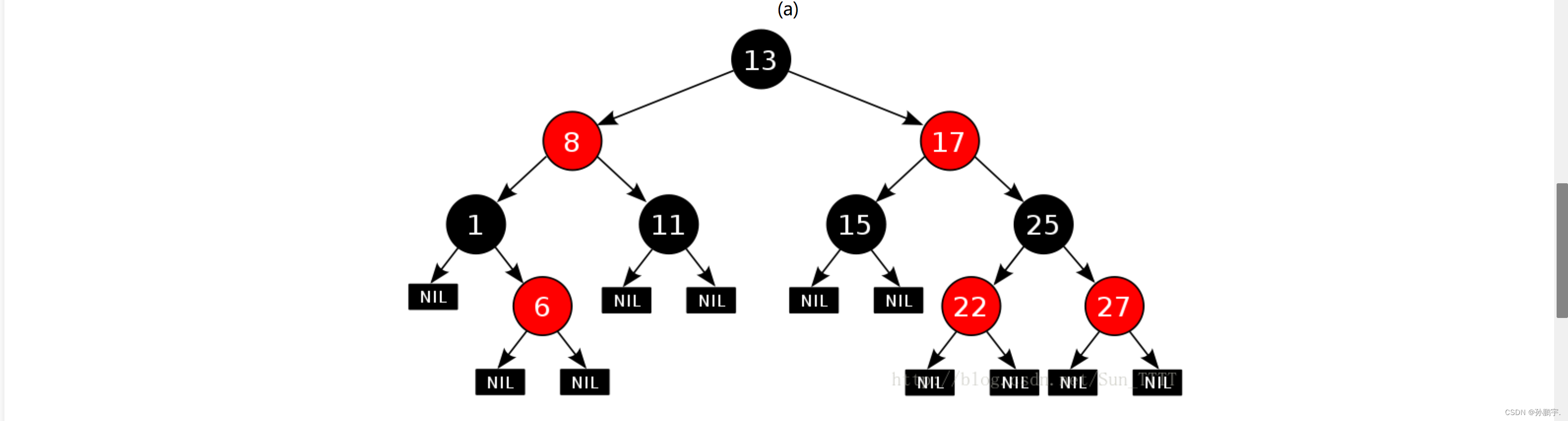
NIL节点有什么作用?如图(a-2),有多少条路径: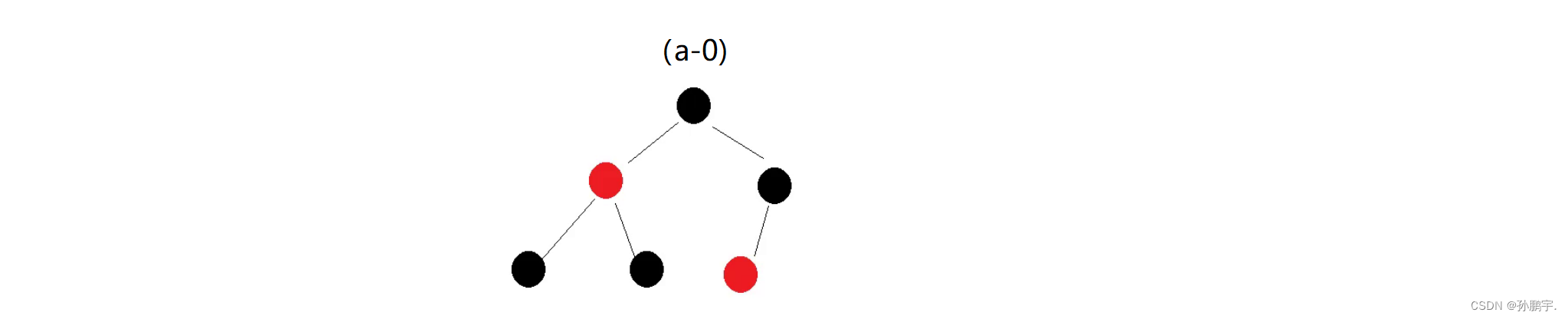
正确答案是有7条。路径路径的判断规则是:从根节点到NULL。
如果我们把NIL节点标记出来就好找路径了:

再比如,图(a-3)是否是红黑树:
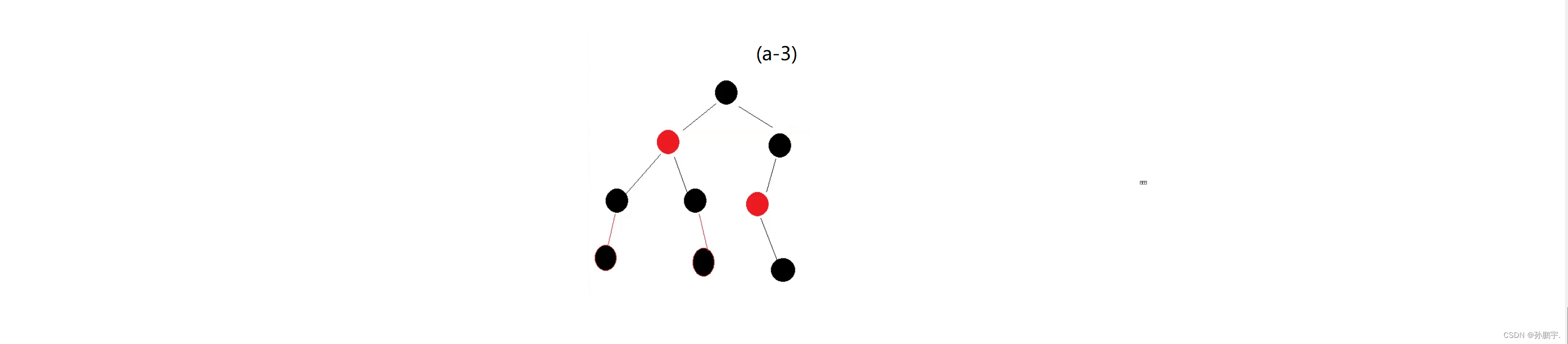
大致一看好像是,但是把NIL节点标出来之后:

路径(b)只有两个黑色节点,不满足红黑树的性质,不是红黑树。
红黑树的最短最长路径
那么红黑树的最短路径是什么样子的,应该是全黑的最短:
那最长的路径呢,应该是一黑一红间隔排列的最长:
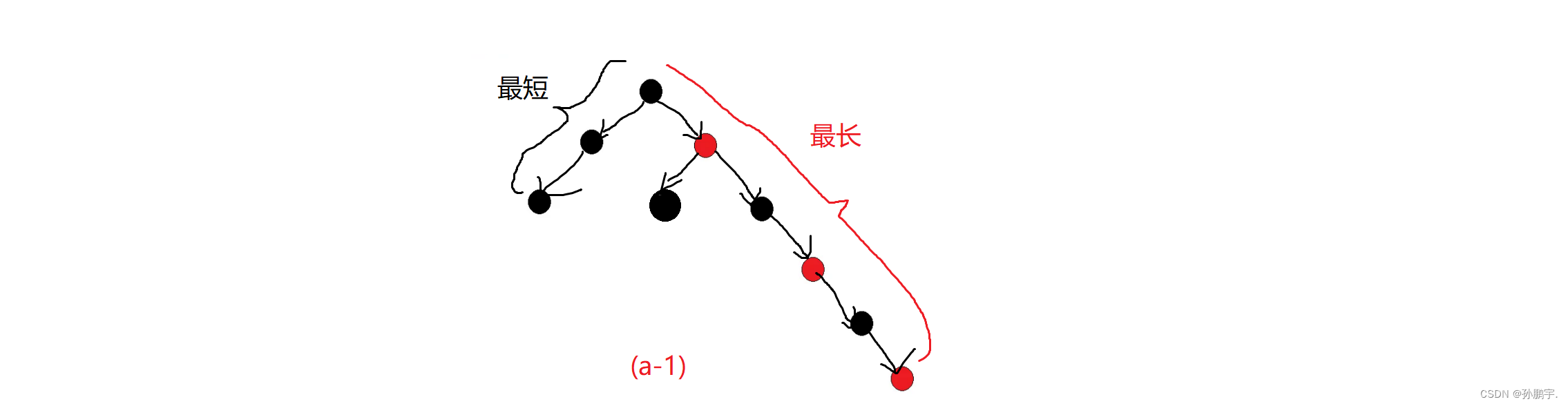 根据图(a-1)我们可以看出,最长的路径是最短的路径的2倍。
根据图(a-1)我们可以看出,最长的路径是最短的路径的2倍。
ps
一个红黑树不一定有最长路径,也不一定有最短路径。
如图(a-2),有最短路径,没有最长路径:
红黑树的路径范围
而知道了最短路径,最长路径,剩下的路径都在最短路径,最长路径范围内,可以写为
[n,2*n]
code
结构
template<class K,class V>struct RBTreeNode
{RBTreeNode<K,V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* parent;pair<K, V>;Color _col;//初始话列表RBTreeNode(const pair<K, V>kv):_left(nullptr),_right(nullptr), _parent(nullptr), pair<K, V>,_col(RED){}
};
搞颜色
enum Color
{RED,BALACK
};类
template<class K,class V>class RBTree{typedef RBTreenode<k,v> Node;public:private:Node* _root = nullptr;};插入
插入逻辑
如果节点为空,就给黑色。如果节点不为空,就插入值。
这个值如果比根节点小,就往左边插入,否则就往右边插入。
bool Insert(const pair<K, v>& kv){if (_root == nullptr){_root = new(kv);_root->_col = BALACK;return true;}//初始化父亲节点和根节点Node* parent = nullptr;Node* cur = _root;while (cur){//key值大,往右走if (cur->kv.first < kv.first){cur = cur->right;}//key值小,往左走else if (cur->kv.first > kv.first){cur = -cur->left;}//否则key值和当前节点相等,不插入else{return false;}}//找到了返回true1return true; }新插入节点
思考:2. 检测新节点插入后,红黑树的性质是否造到破坏?
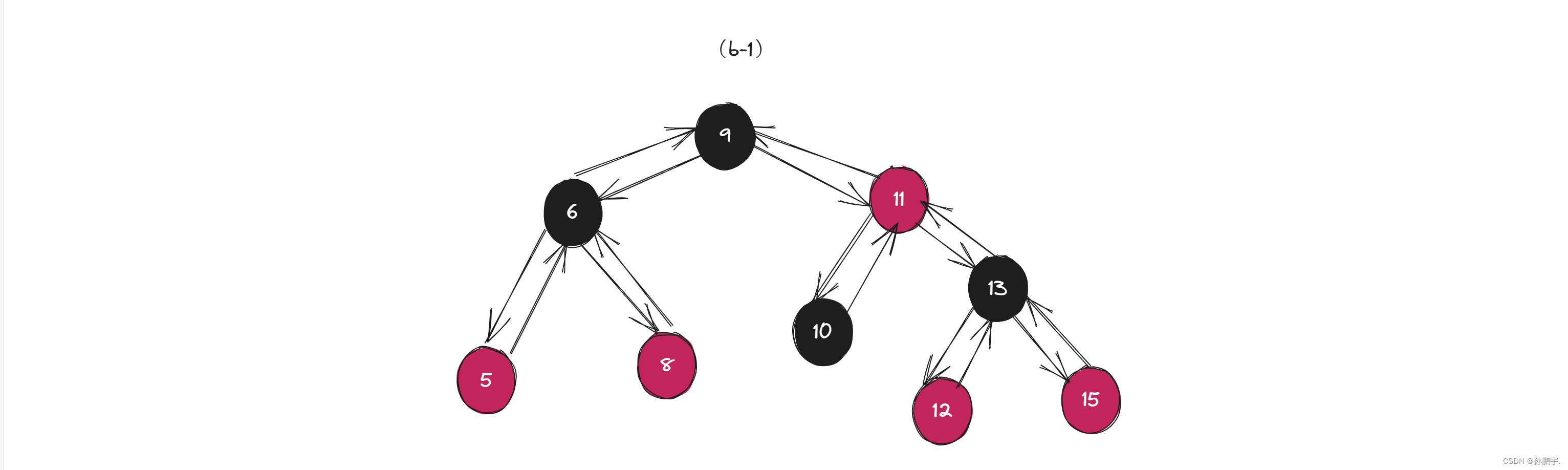
如图(b-1),现在要插入一个节点,那么是插入一个黑色节点还是红色节点呢?
如果插入黑色节点,那么该路径就会多一个黑色节点,根据红黑树特性,其他路径都要补一棵黑色节点,
如果插入红色节点,则只会影响父节点
(即
1.如果父节点也会红节点。两个红节点不能紧挨,需调整
2.如果父亲节点是黑色,则不需调整,直接插入。)。
我们看一下怎么调整,如图(b-2),新插入了一个红色节点7:
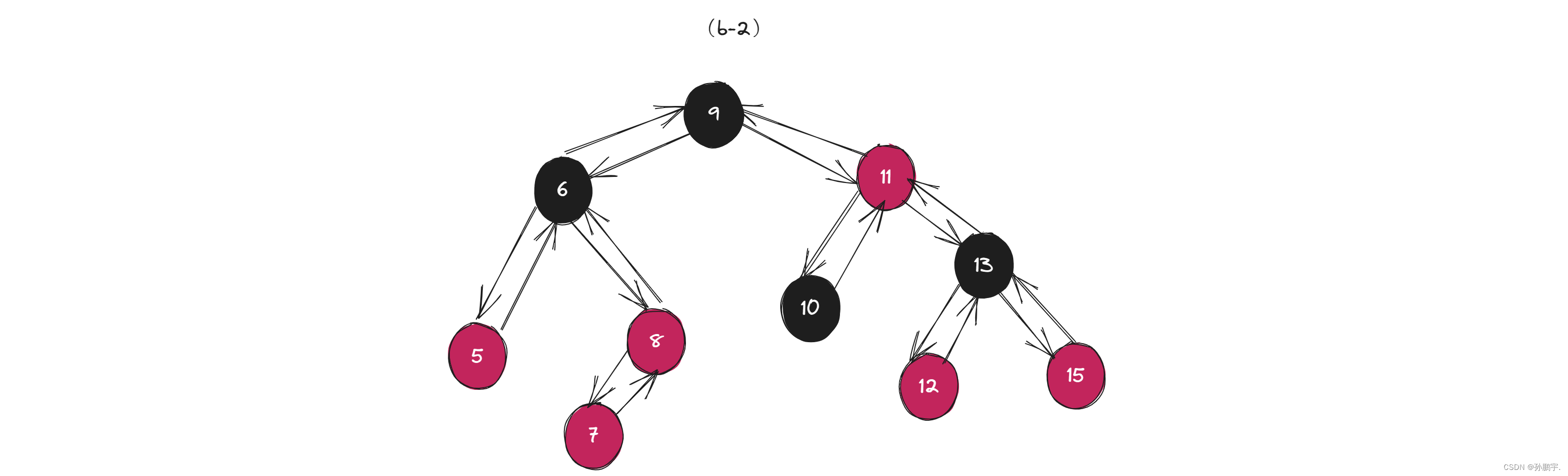
解决方法
能变色先变色,变色完之后还不行再旋转
变色
如图(b-3),先把父节点8变黑:
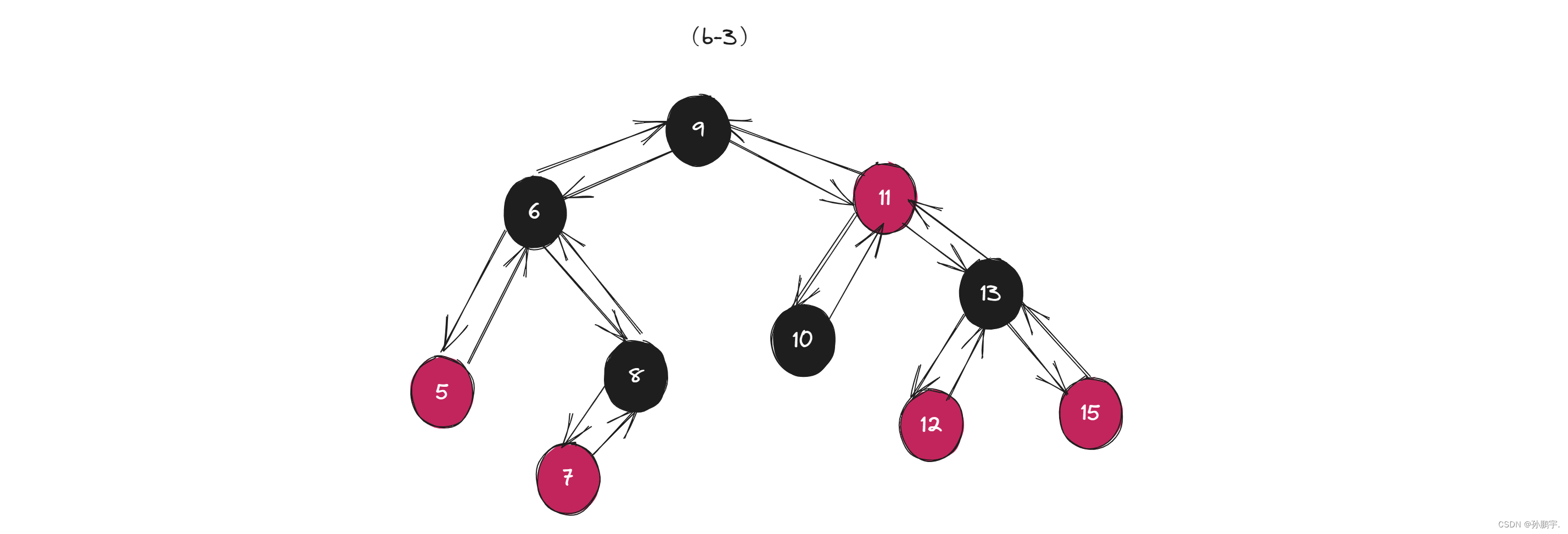
这个时候该路径就多了一个黑色节点,再变图(b-4)把6节点变红:
 这个时候该路径又少了个黑色节点,再变图(b-5) 把5节点变黑:
这个时候该路径又少了个黑色节点,再变图(b-5) 把5节点变黑:
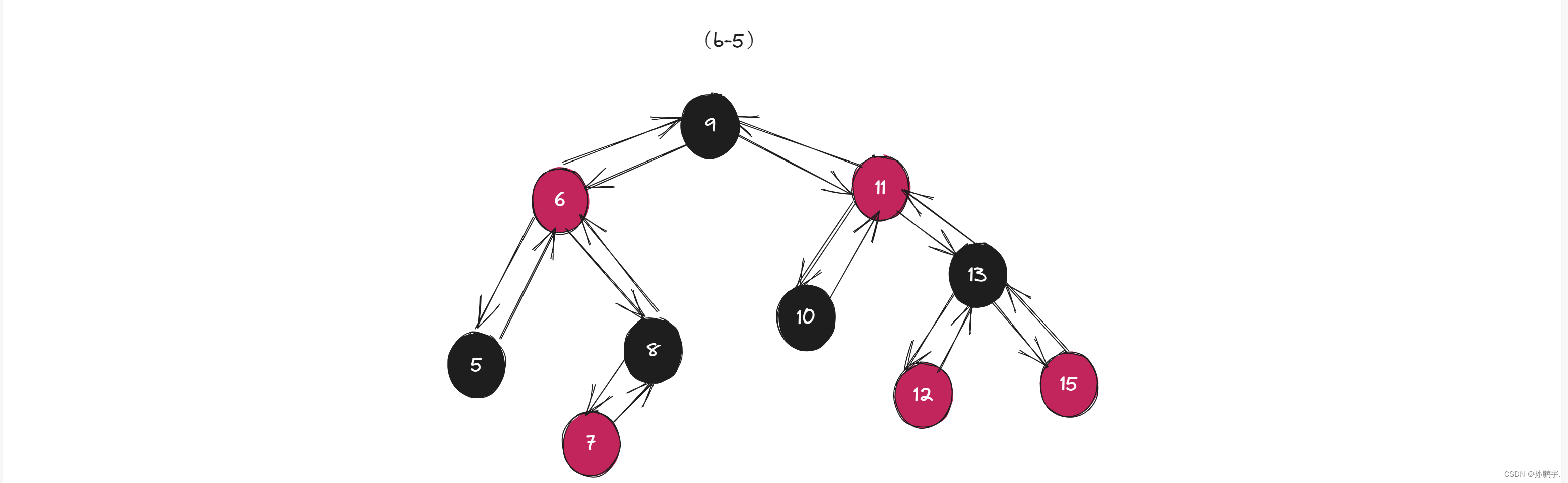
旋转+变色
第二种情况,例如图(b-6):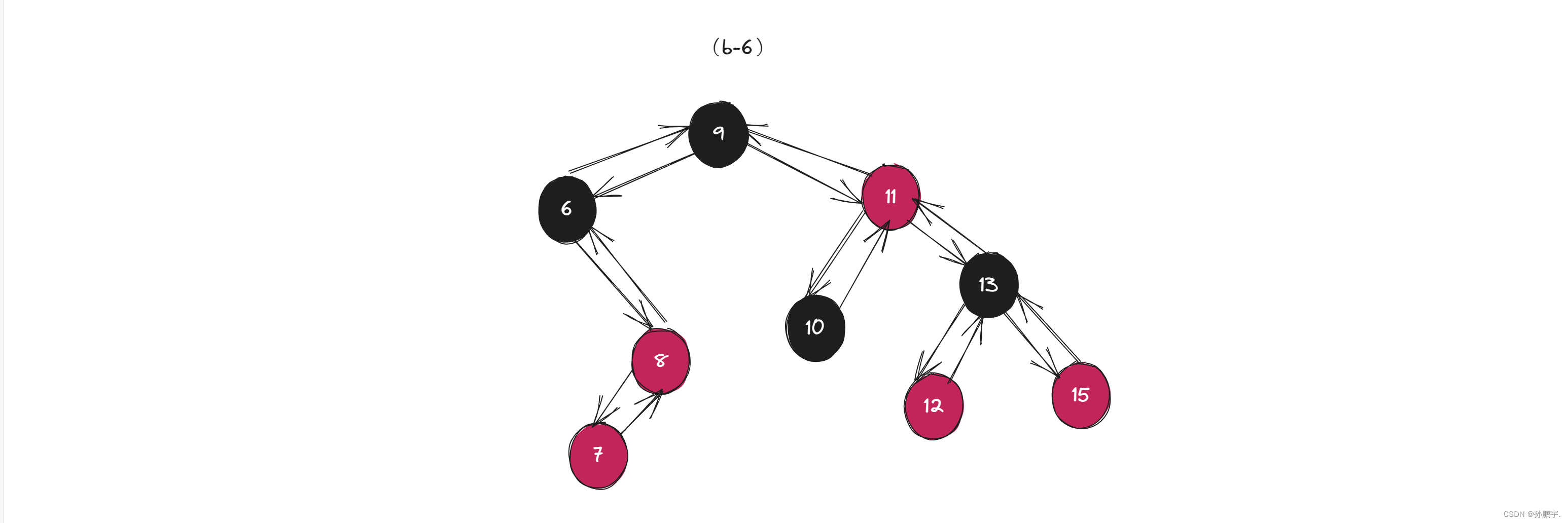 如果还是把父节点变为黑色,把6节点变为红色,那么其他路径就会多一个黑色节点。
如果还是把父节点变为黑色,把6节点变为红色,那么其他路径就会多一个黑色节点。
而该路径又没有其他节点可以再变黑色来平衡这种状态,所以靠变色解决不了这个问题。
这个时候就要旋转了。
先右旋为图(c-1):
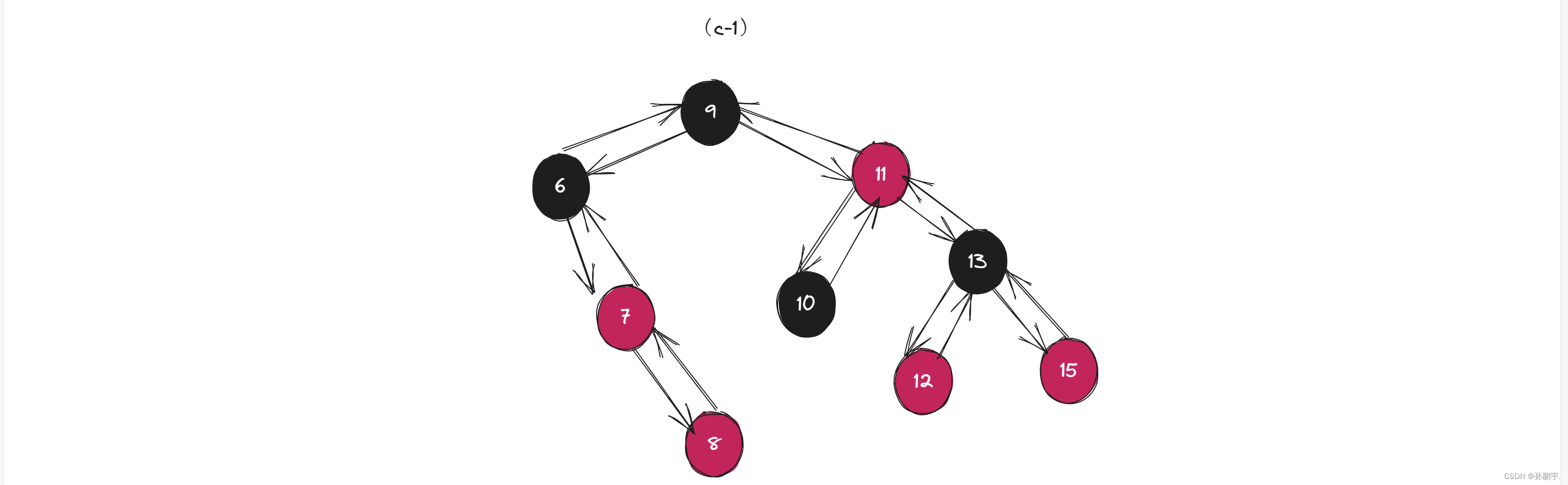 再左旋为图(c-2):
再左旋为图(c-2):
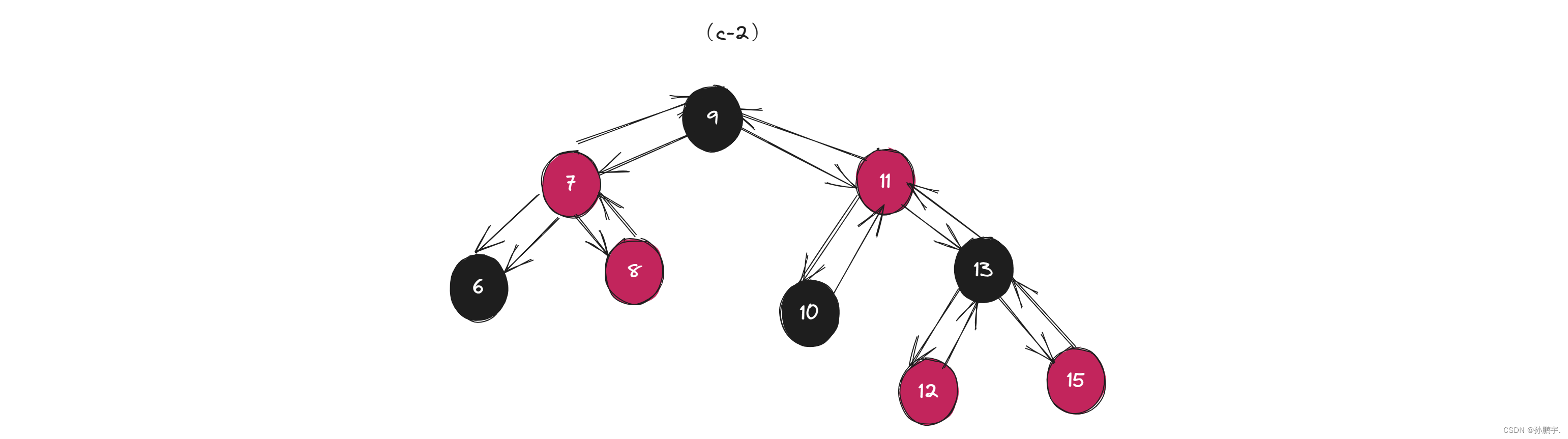 然后再变色为图(c-4):
然后再变色为图(c-4):
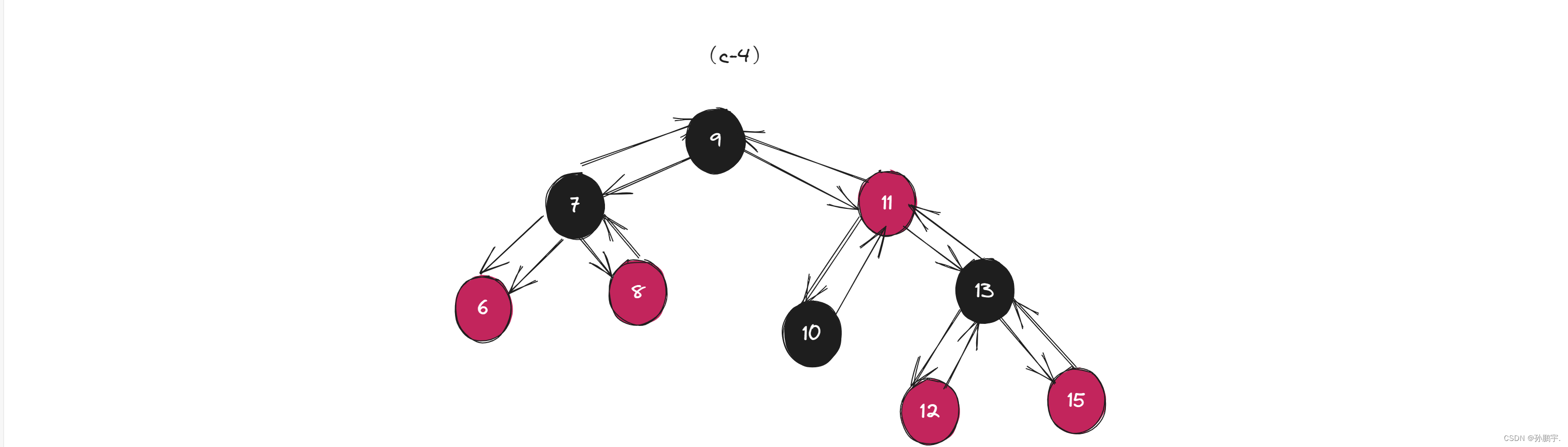
情况一: cur为红,p为红,g为黑,u存在且为红
解决:叔叔存在, 变色

如图(d-0),新插入了一个节点cur:
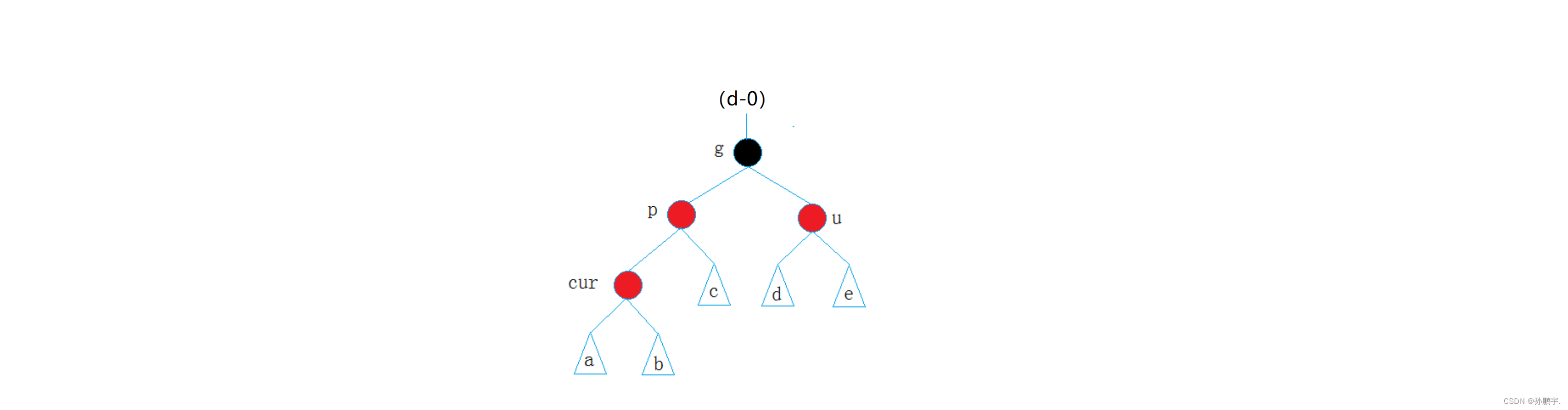
cur为红色节点,那就需要调整。
把p节点变为黑色节点,那么u节点也要变为黑色节点,那么此时就要把g节点变为红色节点。也就是图(d-1):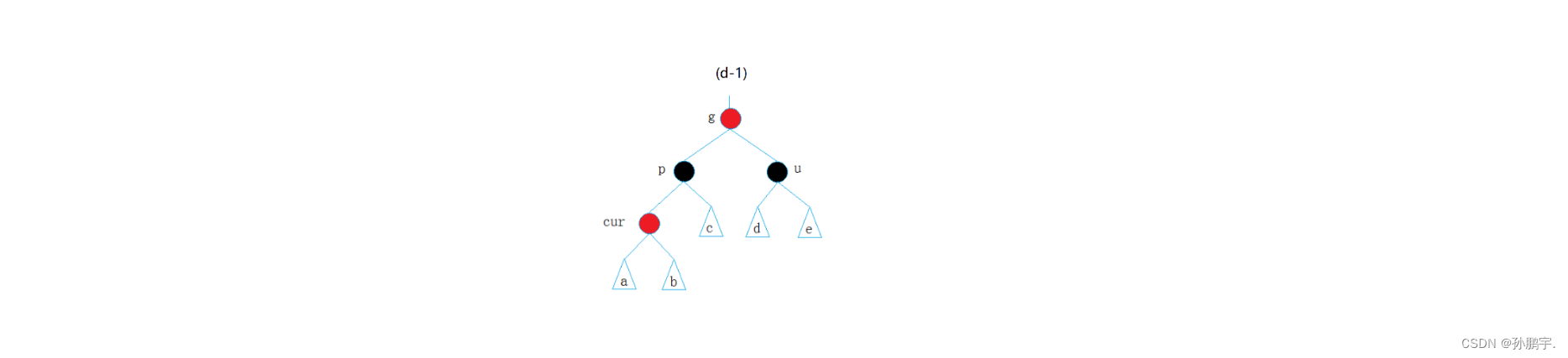
为什么要把g节点变为红色节点呢?
假设g节点不变为红色也就是图(d-3):
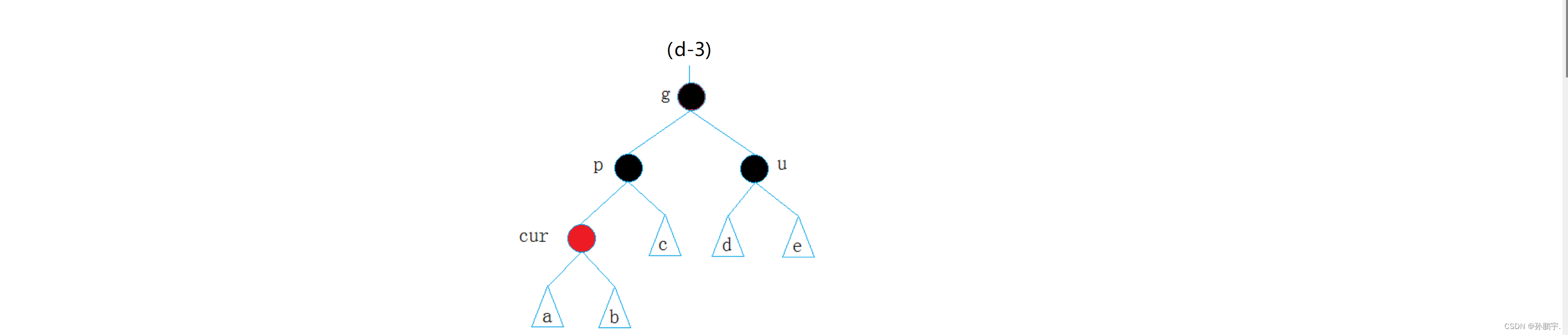
由图(d-1)变为图(d-3)我们发现每条路径凭空多了1个黑色节点。
g节点上面还有节点,那么多了个黑色节点,就会影响上面的路径,所以需要把g节点变红来平衡一下。
如图(d-1):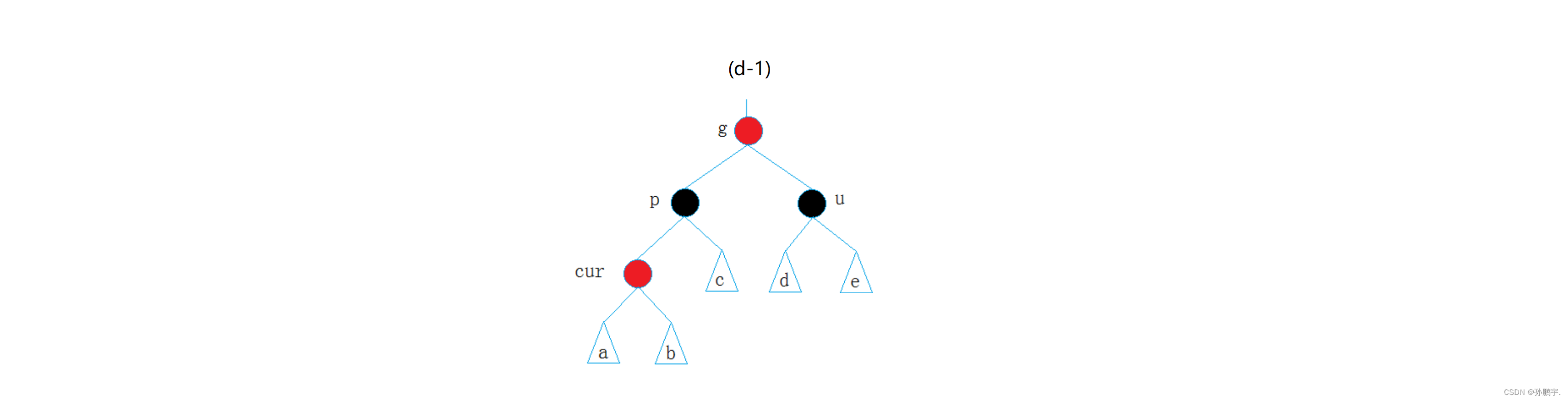
这个时候万一g节点的父节点是红色节点,如图(d-4): 两个红色节点不能连续,还要调整,如果g节点的父亲节点为黑色,如图(d-5),那就不需要再调整:
两个红色节点不能连续,还要调整,如果g节点的父亲节点为黑色,如图(d-5),那就不需要再调整:

新增节点给红色:
cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){paret->_right = cur;cur->_parent = parent;}else if (_parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}父亲节点是红色就调整,是黑色就不用调整:
while (parent->_col = RED){}父亲节点可能在左边(e-1),也可能在右边(e-2):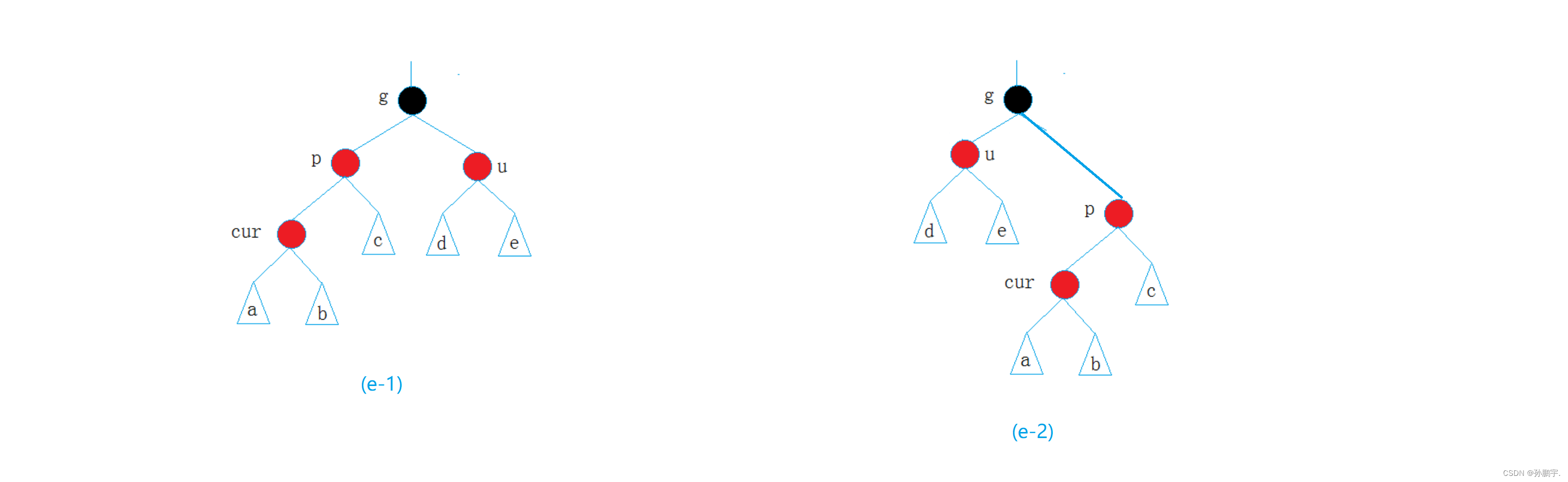 但是不论父亲节点在左在右,父亲节点的父亲父亲节点肯定是granparent节点。
但是不论父亲节点在左在右,父亲节点的父亲父亲节点肯定是granparent节点。
先说图(e-1)的情况(即父亲节点在左):
按照之前的推演,应该先把父亲节点和叔叔节点变为黑色,然后为了防止影响了上面的节点,还要把grandparent节点变为红色:
while (parent&& parent->_col = RED) //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况,叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (unlce && unluce->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡,要把父亲节的颜色变为红色即变为图(d-1):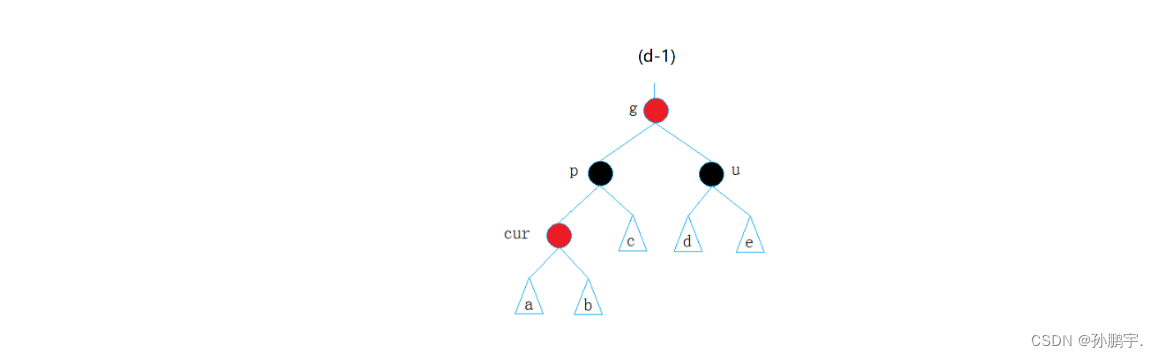
此时又有两种情况 (d-4),(d-5):

(d-4)(d-5)的情况会在后续处理。
继续向上处理
这个时候把祖父节点当做当前节点,让祖父节点去找它的父亲
}while (parent&& parent->_col = RED) //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况,叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (unlce && unluce->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡,要把父亲节的颜色变为红色//继续向上处理cur = grandparent; //把祖父节点当做当前节点parent = cur->parent; //祖父节点去找它的父亲}}}
这个时候万一祖父节点向上不再有节点,祖父节点就是最终节点怎么办?
祖父节点若上面没有节点,那么祖父节点就是作为根节点,根节点不能为红,把根节点再变黑。(r如图(D-5):
while (parent->_col = RED){Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况,父亲节点是左子树,叔叔节点是右子树{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边uncle->_col=parent->_col= BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡,要把父亲节的颜色变为红色}//把祖父当成当前节点,继续向上处理cur = grandparent;}//祖父节点向上不再有节点,祖父节点作为根节点,必须为黑色_root->_col = BACK;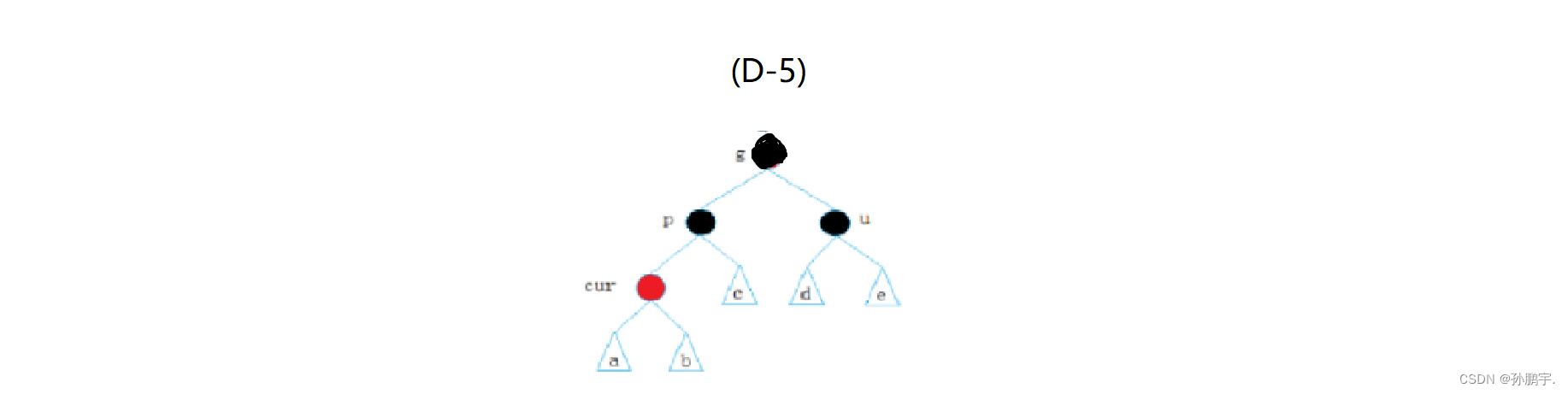
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
解决:把祖父右旋走 ,让父亲做新根,根就要为黑色节点,再把父亲变黑:
图(0-0)到(0-1)为演变过程: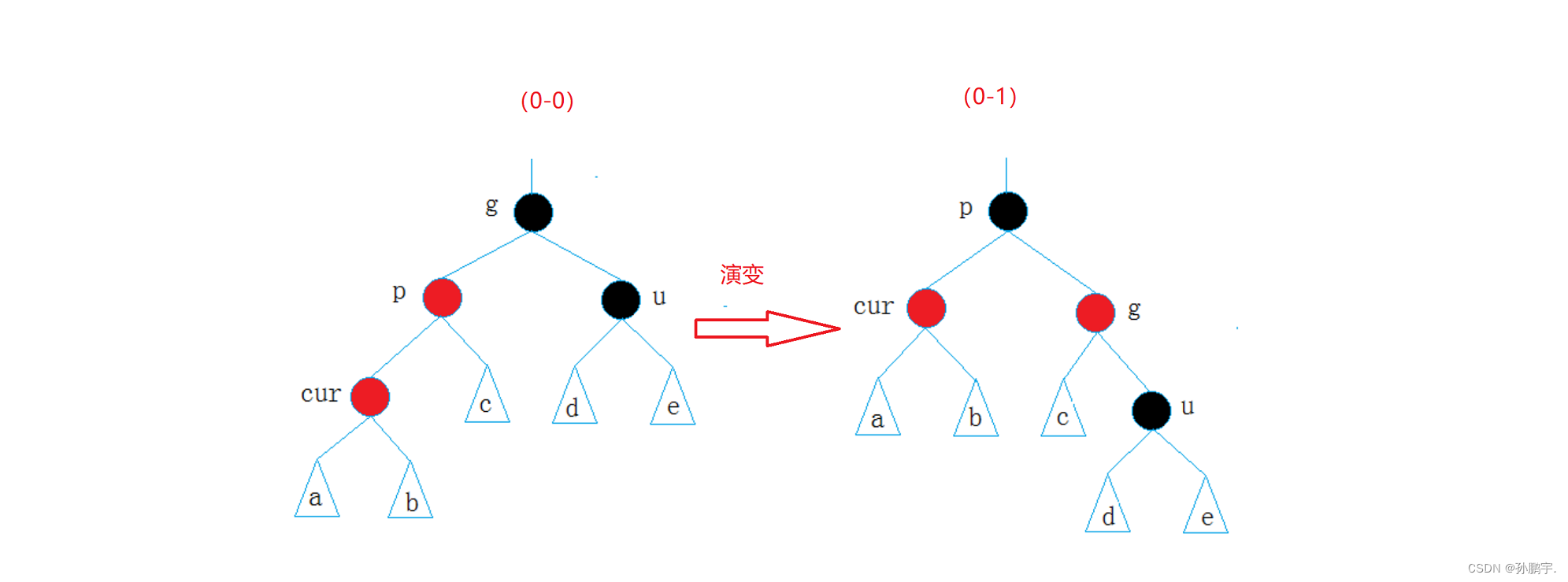
while (parent&& parent->_col = RED) //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况,叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (unlce && unluce->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡,要把父亲节的颜色变为红色//继续向上处理cur = grandparent; //把祖父节点当做当前节点parent = cur->parent; //祖父节点去找它的父亲}else //第二种情况:叔叔节点在左边{if (cur == parent->left) //当前节点在父亲节点的左边{ //单旋+变色 RotateR(granparent); //旋转:把祖父右旋走,让父亲做新根parent->_col = BLACK; //变色:做新根就要为黑色节点grandparent->_col = RED; //祖父为了平衡变红}}}}//祖父节点向上不再有节点,祖父节点作为根节点,必须为黑色_root->_col = BLACK;情况三:p为g的左孩子,cur为p的右孩子(如图e-1)
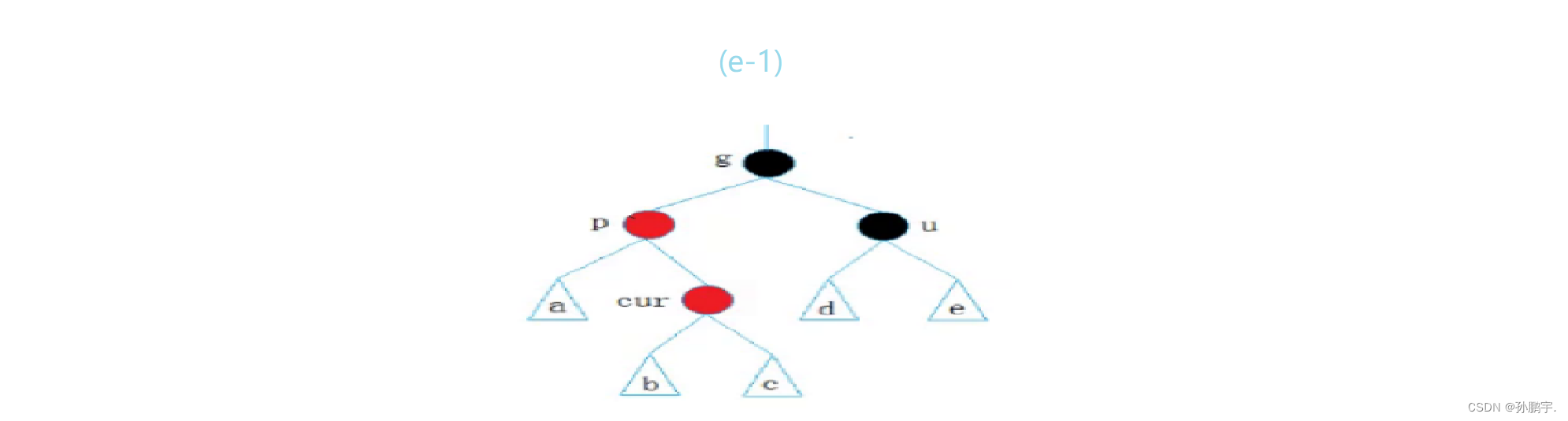
解决方案
(A)p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,
(B)p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
图(e-1)符合(A)解决方案,以下是对图(e-1)用(A)方案进行推演的过程: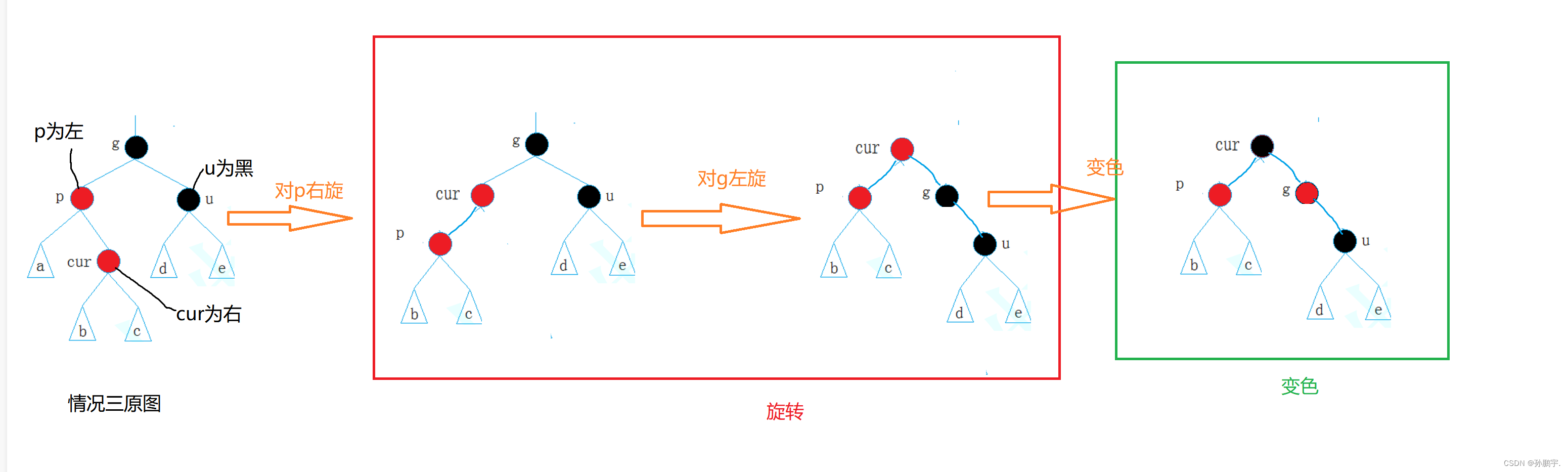
else 父亲在右边
如图(f-3):
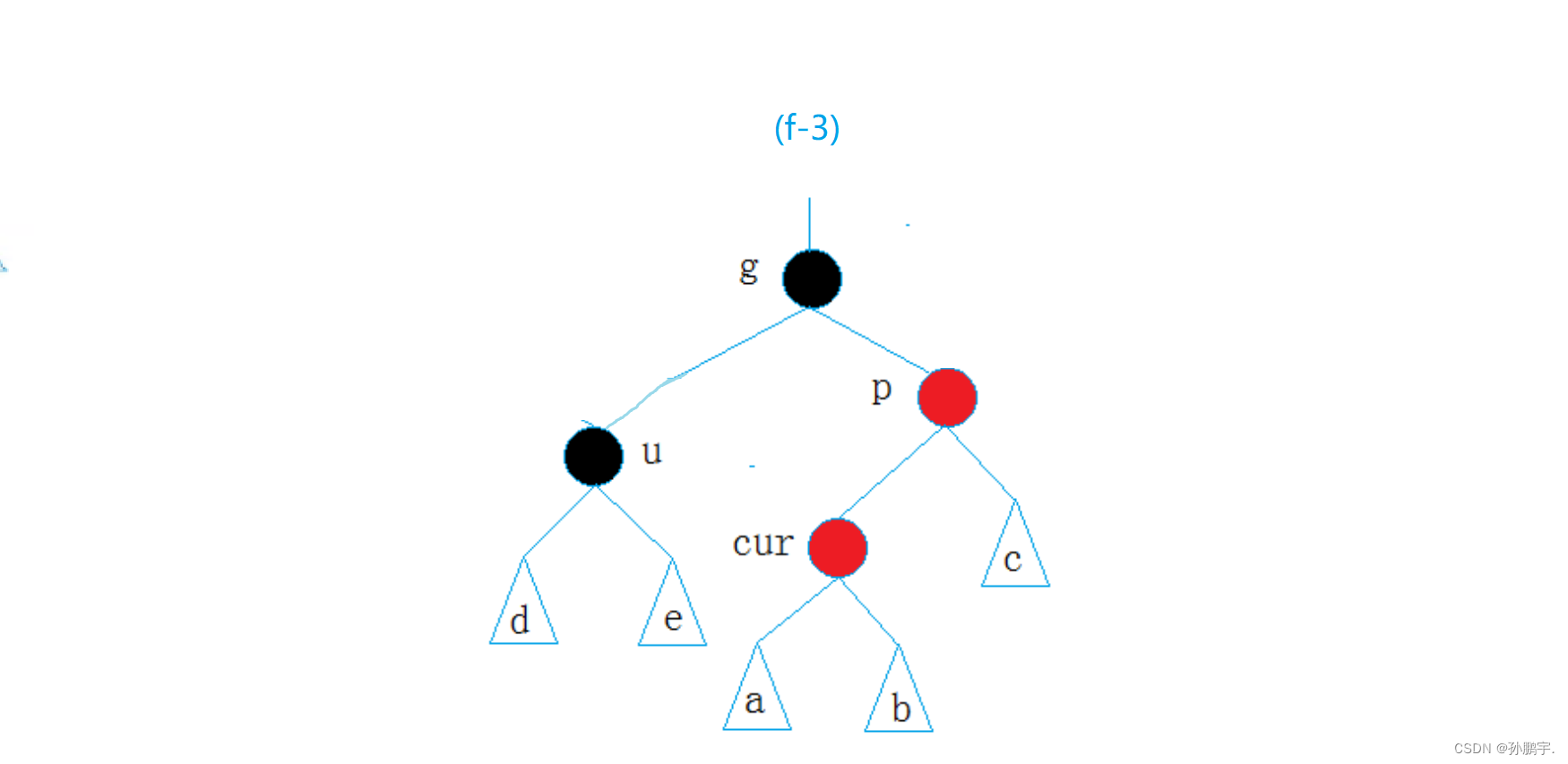
while (parent&& parent->_col == RED) //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况,叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡,要把父亲节的颜色变为红色//继续向上处理cur = grandparent; //把祖父节点当做当前节点parent = cur->_parent; //祖父节点去找它的父亲}else //第二种情况:叔叔节点在左边{if (cur == parent->_left) //当前节点在父亲节点的左边{ //单旋+变色 RotateR(grandparent); //旋转:把祖父右旋走,让父亲做新根parent->_col = BLACK; //变色:做新根就要为黑色节点grandparent->_col = RED; //祖父为了平衡变红}else //当前节点在父亲节点右边{ //双旋 RotateL(parent); //父亲右旋RotateR(grandparent); //祖父右旋cur->_col = BLACK; //当前节点变黑grandparent->_col = RED; //祖变红}break;}}else //父亲在右边{Node* uncle = grandparent->_left;//叔叔节点在祖父节点的右边if (uncle = grandparent->_left) //叔叔在左边//变色if (uncle && uncle->_col == parent->_col == RED) //if叔叔存在且颜色为红色{uncle->_col = parent->_col = BLACK; //叔叔父亲都变黑grandparent->_col = RED; //祖父上面还有节点,要变红//继续向上处理cur = grandparent;}else //叔叔颜色为黑色{if (cur = parent->_right) //叔叔在右边{RotateL(grandparent); //左旋爷 parent->_col = BLACK;grandparent->_col = RED; //祖变红}else //叔叔在左边{// g// u p// cRotateR(parent); // 父亲右旋RotateL(grandparent); //祖父旋走,让cur当根cur->_col = BLACK; //根变黑色grandparent->_col = RED; //祖父为了平衡变红色}}}}//祖父节点向上不再有节点,祖父节点作为根节点,必须为黑色_root->_col = BLACK;//找到了返回true1return true;
}相关文章:

C++ RBTree 理论
目录 这个性质可以总结为 红黑树的最短最长路径 红黑树的路径范围 code 结构 搞颜色 类 插入 插入逻辑 新插入节点 思考:2. 检测新节点插入后,红黑树的性质是否造到破坏? 解决方法 变色 旋转变色 第三种情况,如果根…...

制作这种在线宣传画册,可轻松收获客户!
制作企业宣传画册,首先要了解企业制作宣传画册的需求以及展示方向,如今互联网时代,宣传画册的制作也应该要创新,而制作一本在线电子宣传画册用于线上宣传是非常有必要的。如何制作呢? 我们 可以使用FLBOOK平台在线制作…...
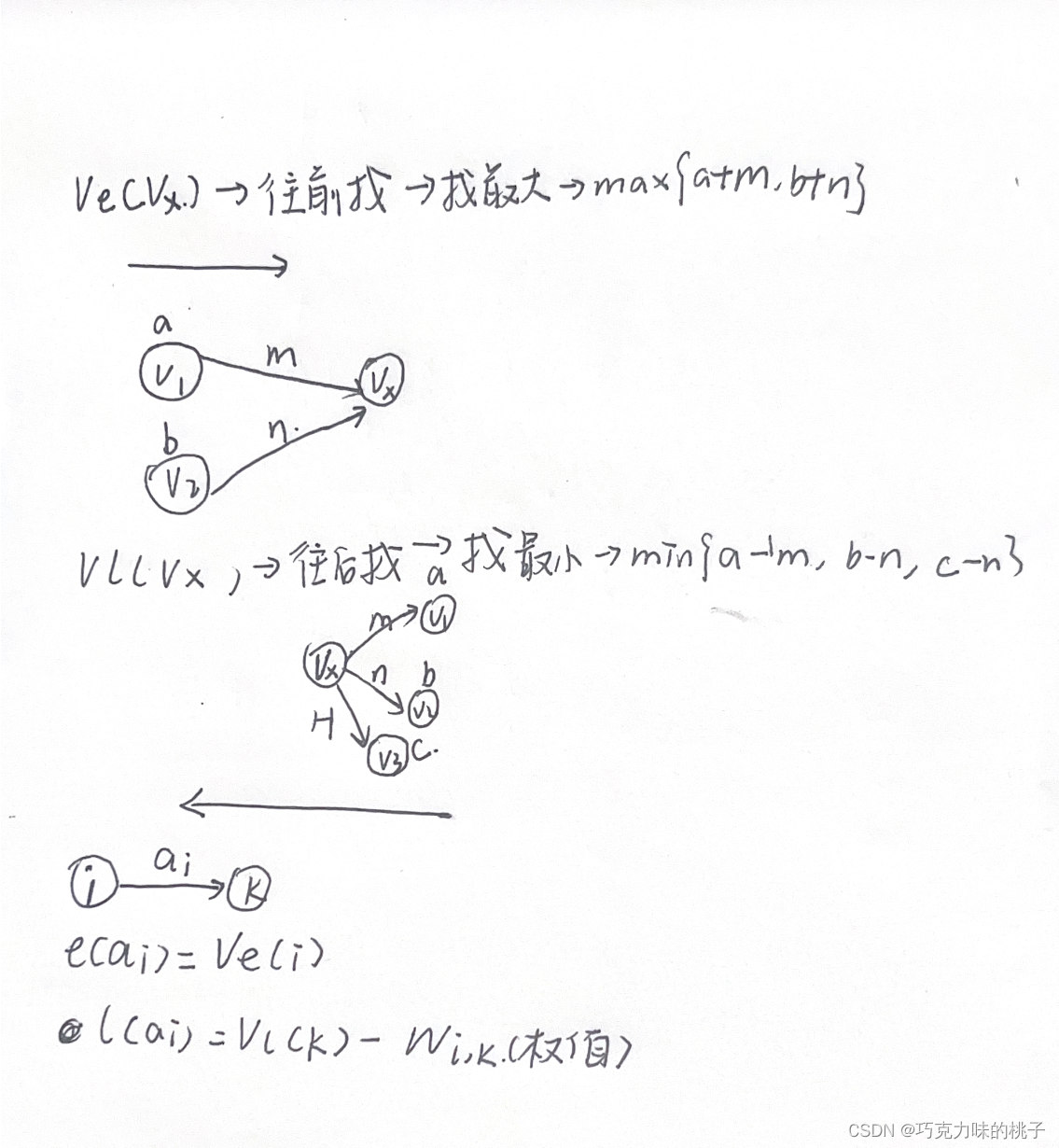
数据结构 | 图
最小生成树算法 Prime算法 算法思路:从已选顶点所关联的未选边中找出权重最小的边,并且生成树不存在环。 其中,已选顶点是构成最小生成树的结点,未选边是不属于生成树中的边。 例子: 第一步: 假设我们从顶…...

[文件读取]shopxo 文件读取(CNVD-2021-15822)
1.1漏洞描述 漏洞编号CNVD-2021-15822漏洞类型文件读取漏洞等级⭐⭐漏洞环境VULFOCUS攻击方式 描述: ShopXO是一套开源的企业级开源电子商务系统。 ShopXO存在任意文件读取漏洞,攻击者可利用该漏洞获取敏感信息。 1.2漏洞等级 高危 1.3影响版本 ShopXO 1.4漏洞复现…...

zookeeper应用之分布式锁
在分布式系统中多个服务需要竞争同一个资源时就需要分布式锁,这里使用zookeeper的临时顺序节点来实现分布式锁。 在节点X下创建临时顺序节点,getChildren()获取节点X的所有子节点,判断当前节点是否是第一个子节点,如果是就获取锁…...

20. 机器学习——PCA 与 LDA
机器学习面试题汇总与解析——PCA 与 LDA 本章讲解知识点 什么是数据降维PCA本专栏适合于Python已经入门的学生或人士,有一定的编程基础。 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。 本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。这才是一…...

深度学习准召
准确率(Precision)和召回率(Recall)是两个用来评价一个模型的好坏的指标,它们有不同的意义: 准确率(Precision):准确率是在所有被模型判断为正例的样本中,有…...

AtCoder ABC154
C - Distinct or Not 签到题,注意大小写和以前的不一样 D - Dice in Line 签到题2,用个窗口即可 E - Almost Everywhere Zero 数位DP(搜索)的例题 pos表示当前搜索到的位置(开始为0,结束为n) …...

可以非常明显地感受到,一场有关直播带货的暗流正在涌动
虽然有关直播带货的争论依然还在持续,但是,我们依然无法否认今年的双十一依然是直播带货的高光时刻。无论是以淘宝、京东和拼多多为代表的传统电商平台,还是以抖音、快手为代表的新电商平台,几乎都将今年双十一的重心放在了直播带…...

C++中的四种构造函数
在C中,有几种不同类型的构造函数,基于它们的特性和用途,可以将它们分类为以下四种: 默认构造函数(Default Constructor): 如果没有为类定义任何构造函数,编译器将为其提供一个默认构造函数。这种…...

通过反射获取某个对象属性是否存在,并获取对象值
SneakyThrowspublic static void main(String[] args) {User user new User("张三", 10);// 获取指定属性名的值String propertyName "name2";Field[] fields user.getClass().getDeclaredFields();// 输出属性名Boolean flag false;for (Field field …...

【MySQL】存储过程与函数
一、存储过程 1、什么是存储过程 它是一组经过预先编译的SQL的封装它被存储在MySQL服务器上,当需要执行它时,客户端只需要向服务器发出调用命令,就可以把这一系列预先存储好的SQL语句全部执行 2、存储过程的优缺点 优点 简化操作…...

【数学】Pair of Topics—CF1324D
Pair of Topics—CF1324D 思路 很明显,需要对 a i a j > b i b j a_i a_j > b_i b_j aiaj>bibj 化简: a i − b i > b j − a j a_i - b_i > b_j - a_j ai−bi>bj−aj a i − b i > − ( a j − b j ) a_…...
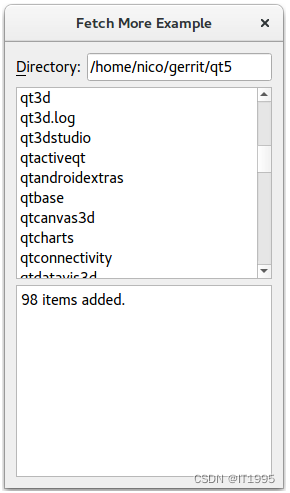
Qt文档阅读笔记-Fetch More Example解析
Fetch More Example这个例子说明了如何在视图模型上添加记录。 这个例子由一个对话框组成,在Directory的输入框中,可输入路径信息。应用程序会载入路径信息的文件信息等。不需要按回车键就能搜索。 当有大量数据时,需要对视图模型进行批量增…...

QtC++与QTableView详解
介绍 QTableView 是 Qt 框架中用于显示表格数据的视图控件,它是 QAbstractItemView 类的子类。QTableView 通常与 QStandardItemModel 或者自定义的数据模型一起使用,用于展示二维表格型数据。以下是对 QTableView 的详细讲解和在 Qt 中的作用ÿ…...

HG/T 6002-2022 氟树脂粉末涂料检测
氟树脂粉末涂料是指以三氟氯乙烯-乙烯基醚、四氟乙烯-乙烯基醚等交联型氟树脂或聚偏二氟乙烯PVDF树脂为主要成膜物质,可加入颜料、填料、助剂、固化剂等制成的粉末涂料,主要用于铝型材、幕墙金属板、家电等表面的装饰和保护。 HG/T 6002-2022 氟树脂粉末…...

【java】idea可以连接但看不到database相关的files
问题 idea右侧有database工具栏,但点击没有在recent files看到数据库相关文件 问题排查 点击 help-> show log in explorer查看日志 发现显示 2023-11-13 10:28:09,694 [1244376] INFO - #c.i.c.ComponentStoreImpl - Saving appDebuggerSettings took 22…...

信驰达科技加入车联网联盟(CCC),推进数字钥匙发展与应用
CCC)的会员。 图 1 深圳信驰达正式成为车联网联盟(CCC)会员 车联网联盟(CCC)是一个跨行业组织,致力于推动智能手机与汽车连接解决方案的技术发展。CCC涵盖了全球汽车和智能手机行业的大部分企业,拥有150多家成员公司。CCC成员公司包括智能手机和汽车制造…...

p9 Eureka-搭建eureka服务
1.在user-service项目引入spring-cloud-starter-netflix-eureka-client的依赖 <dependencies><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></depen…...
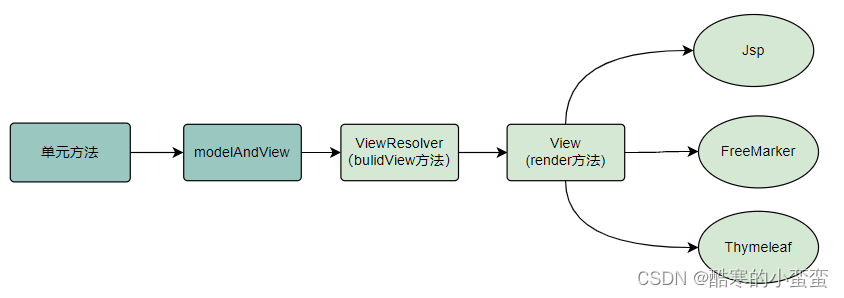
阶段七-Day01-SpringMVC
一、Sping MVC的介绍 1. 使用Front(前端)设计模式改写代码 1.1 目前我们的写法 目前我们所写的项目,持久层、业务层的类都放入到Spring容器之中了。他们之间需要注入非常方便,只需要通过Autowired注解即可。 但是由于Servlet整个生命周期都是被Tomca…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
