【LeetCode】26. 删除有序数组中的重复项
26. 删除有序数组中的重复项
难度:简单
题目
给你一个 非严格递增排列 的数组 nums ,请你原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案int k = removeDuplicates(nums); // 调用assert k == expectedNums.length;
for (int i = 0; i < k; i++) {assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 10^4-10^4 <= nums[i] <= 10^4nums已按 非严格递增 排列
个人题解
思路:
- 定义一个指针
l表示左区域的右边界,即在l左边的数都是不重复的数 - 遍历数组,当前数与上面右边界不相等时,则右边界扩大一位,并把当前数赋值给新的右边界
- 有效数组大小即
右边界索引值 + 1
class Solution {public int removeDuplicates(int[] nums) {int l = 0;for (int i = 1; i < nums.length; i++) {if (nums[l] != nums[i]) {nums[++l] = nums[i];}}return l + 1;}
}
官方题解
方法一:双指针
这道题目的要求是:对给定的有序数组 nums 删除重复元素,在删除重复元素之后,每个元素只出现一次,并返回新的长度,上述操作必须通过原地修改数组的方法,使用 O(1)的空间复杂度完成。
由于给定的数组 nums 是有序的,因此对于任意 i < j ,如果 num[i] == num[j] ,则对任意 i <= k <= j,必有 num[i] = num[k] = nums[j],即相等的元素在数组中的下标一定是连续的。利用数组有序的特点,可以通过双指针的方法删除重复元素。
如果数组 nums 的长度为 0,则数组不包含任何元素,因此返回 0。
当数组 nums 的长度大于 0 ,时,数组中至少包含一个元素,在删除重复元素之后也至少剩下一个元素,因此 nums[0] 保持原状即可,从下标 1 开始删除重复元素。
定义两个指针 fast 和 slow 分别为快指针和慢指针,快指针表示遍历数组到达的下标位置,慢指针表示下一个不同元素要填入的下标位置,初始时两个指针都指向下标 1 。
假设数组 nums 的长度为 n 。将快指针 fast 依次遍历从 1 到 n - 1的每个位置,如果 nums[fast] != nums[fast - 1],说明 num[fast] 和之前的元素都不同,因此将 nums[fast] 的值复制到 nums[slow],然后将 slow 的值加 1,即指向下一个位置。
遍历结束之后,从 nums[0] 到 num[slow - 1] 的每个元素都不相同且包含原数组中的每个不同的元素,因此新的长度即为 slow,返回 slow即可。
class Solution {public int removeDuplicates(int[] nums) {int n = nums.length;if (n == 0) {return 0;}int fast = 1, slow = 1;while (fast < n) {if (nums[fast] != nums[fast - 1]) {nums[slow] = nums[fast];++slow;}++fast;}return slow;}
}
作者:力扣官方题解
链接:https://leetcode.cn/problems/remove-duplicates-from-sorted-array/solutions/728105/shan-chu-pai-xu-shu-zu-zhong-de-zhong-fu-tudo/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

【LeetCode】26. 删除有序数组中的重复项
26. 删除有序数组中的重复项 难度:简单 题目 给你一个 非严格递增排列 的数组 nums ,请你原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素…...

K8S知识点(八)
(1)实战入门-Label 通过标签实现Pod的区分,说白了就是一种标签选择机制 可以使用命令是否加了标签: 打标签: 更新标签: 筛选标签: 修改配置文件,重新创建一个pod 筛选࿱…...

25.4 MySQL 函数
1. 函数的介绍 1.1 函数简介 在编程中, 函数是一种组织代码的方式, 用于执行特定任务. 它是一段可以被重复使用的代码块, 通常接受一些输入(参数)然后返回一个输出. 函数可以帮助开发者将大型程序分解为更小的, 更易于管理的部分, 提高代码的可读性和可维护性.函数在编程语言…...

Unity 下载Zip压缩文件并且解压缩
1、Unity下载Zip压缩文件主要使用UnityWebRequest类。 可以参考以下方法: webRequest UnityWebRequest.Get(Path1); //压缩文件路径webRequest.timeout 60;webRequest.downloadHandler new DownloadHandlerBuffer();long fileSize GetLocalFileSize(Path2); …...

c++11新特性篇-委托构造函数和继承构造函数
C11引入了委托构造函数(Delegating Constructor)和C11及后续标准引入了继承构造函数(Inheriting Constructor)两个特性。 1.委托构造函数 委托构造函数是C11引入的一个特性,它允许一个构造函数调用同一类的另一个构造…...
案例)
Flink SQL处理回撤流(Retract Stream)案例
Flink SQL支持处理回撤流(Retract Stream),下面是一个使用Flink SQL消费回撤流的案例: 假设有一个数据流,包含用户的姓名和年龄,希望计算每个姓名的年龄总和。 以下是示例代码: // 创建流执行…...
)
6.5.事件图层(MapEventsOverlay)
愿你出走半生,归来仍是少年! 简单来说就是一个不参与绘制但是可进行交互的图层,它具备了单击和长按的交互功能。 booleanonSingleTapConfirmed(MotionEvent e, MapView mapView)booleanonLongPress(MotionEvent e, MapView mapView) 通过继承它重写上方…...
供暖系统如何实现数据远程采集?贝锐蒲公英高效实现智慧运维
山西某企业专注于暖通领域,坚持为城市集中供热行业和楼宇中央空调行业提供全面、专业的“智慧冷暖”解决方案。基于我国供热行业的管理现状,企业成功研发并推出了可将能源供应、管理与信息化、自动化相融合的ICS-DH供热节能管理系统。 但是,由…...
Flutter笔记:关于Flutter中的大文件上传(上)
Flutter笔记 关于Flutter中的大文件上传(上) 大文件上传背景与 Flutter 端实现文件分片传输 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址&#…...
腾讯云CVM服务器5年可选2核4G和4核8G配置
腾讯云服务器网整理五年云服务器优惠活动 txyfwq.com/go/txy 配置可选2核4G和4核8G,公网带宽可选1M、3M或5M,系统盘为50G高性能云硬盘,标准型S5实例CPU采用主频2.5GHz的Intel Xeon Cascade Lake或者Intel Xeon Cooper Lake处理器,…...
数据结构:反射
基本概念 反射中的四个类 Class类 Java文件在被编译之后,生成了.class文件,JVM此时解读.class文件,将其解析为java.lang.Class 对象,在程序运行时每个java文件就最终变成了Class类对象的一个实例。通过反射机制应用这个 实例就…...

45 深度学习(九):transformer
文章目录 transformer原理代码的基础准备位置编码Encoder blockmulti-head attentionFeed Forward自定义encoder block Deconder blockEncoderDecodertransformer自定义loss 和 学习率mask生成函数训练翻译 transformer 这边讲一下这几年如日中天的新的seq2seq模式的transform…...

java中用javax.servlet.ServletInputStream.readLine有什么安全问题吗?怎么解决实例?
使用 javax.servlet.ServletInputStream.readLine 方法在处理 Servlet 请求时可能存在以下安全问题,以及相应的解决方案: 缓冲区溢出:readLine 方法会将数据读取到一个缓冲区中,并根据换行符分隔成行。如果输入流中包含过长的行或…...
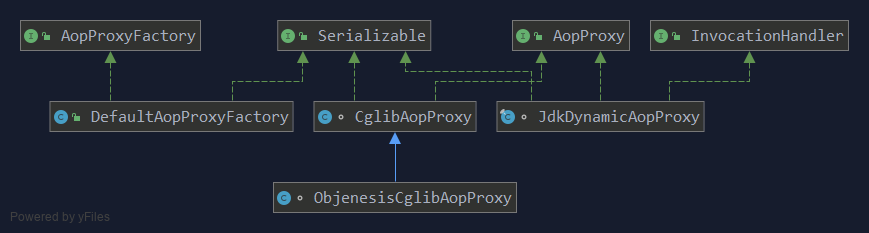
面试官问 Spring AOP 中两种代理模式的区别?很多面试者被问懵了
面试官问 Spring AOP 中两种代理模式的区别?很多初学者栽了跟头,快来一起学习吧! 代理模式是一种结构性设计模式。为对象提供一个替身,以控制对这个对象的访问。即通过代理对象访问目标对象,并允许在将请求提交给对象前后进行一…...
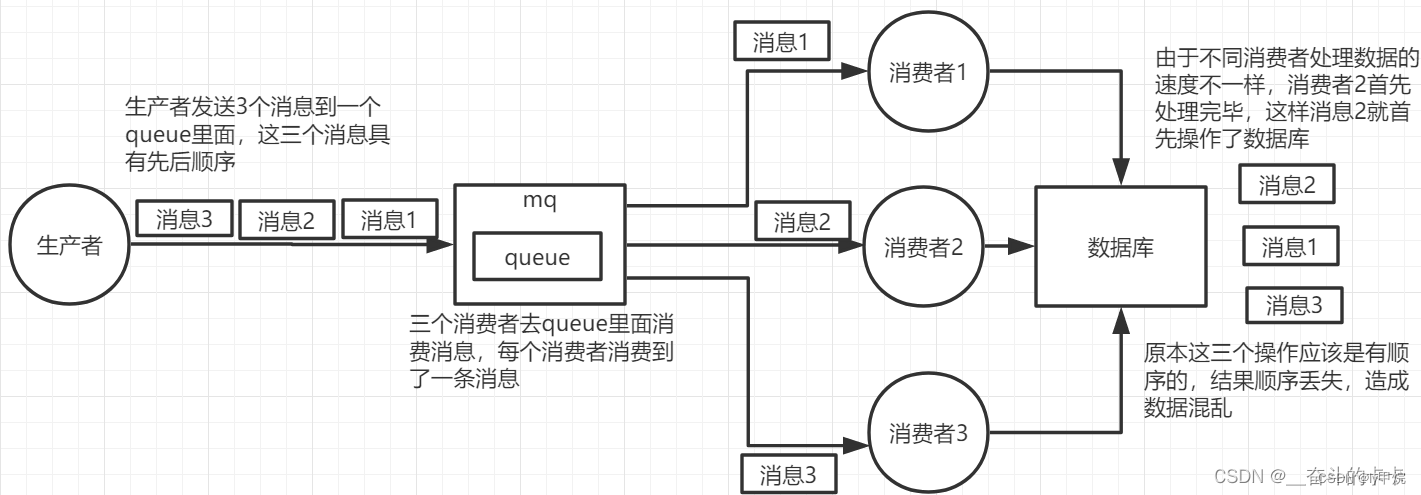
MQ四大消费问题一锅端:消息不丢失 + 消息积压 + 重复消费 + 消费顺序性
RabbitMQ-如何保证消息不丢失 生产者把消息发送到 RabbitMQ Server 的过程中丢失 从生产者发送消息的角度来说,RabbitMQ 提供了一个 Confirm(消息确认)机制,生产者发送消息到 Server 端以后,如果消息处理成功ÿ…...

Python爬虫——入门爬取网页数据
目录 前言 一、Python爬虫入门 二、使用代理IP 三、反爬虫技术 1. 间隔时间 2. 随机UA 3. 使用Cookies 四、总结 前言 本文介绍Python爬虫入门教程,主要讲解如何使用Python爬取网页数据,包括基本的网页数据抓取、使用代理IP和反爬虫技术。 一、…...
爬虫,TLS指纹 剖析和绕过
当你欲爬取某网页的信息数据时,发现通过浏览器可正常访问,而通过代码请求失败,换了随机ua头IP等等都没什么用时,有可能识别了你的TLS指纹做了验证。 解决办法: 1、修改 源代码 2、使用第三方库 curl-cffi from curl…...

Linux shell编程学习笔记25:tty
1 tty的由来 在 1830 年代和 1840 年代,开发了称为电传打字机(teletypewriters)的机器,这些机器可以将发件人在键盘上输入的消息“沿着线路”发送在接收端并打印在纸上。 电传打字机的名称由teletypewriters, 缩短为…...
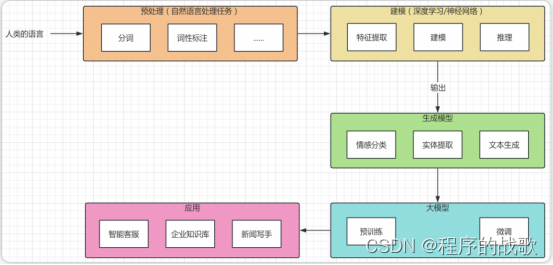
AIGC大模型-初探
大语⾔模型技术链 1. ⾃然语⾔处理 2. 神经⽹络 3. ⾃注意⼒机制 4. Transformer 架构 5. 具体模型 - GPT6. 预训练,微调 7. ⼤模型应⽤ - LangChain 大语⾔模型有什么用? 利⽤⼤语⾔模型帮助我们理解⼈类的命令,从⽽处理⽂本分析…...
Postman for Mac(HTTP请求发送调试工具)v10.18.10官方版
Postman for mac是一个提供在MAC设备上功能强大的开发,监控和测试API的绝佳工具。非常适合开发人员去使用。此版本通过Interceptor添加了对请求捕获的支持,修正了使用上下文菜单操作未复制响应正文的问题和预请求脚本的垂直滚动条与自动完成下拉列表重叠…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
