Flutter的Widget, Element, RenderObject的关系
在Flutter中,Widget,Element和RenderObject是三个核心的概念,它们共同构成了Flutter的渲染流程和组件树的基础。下面简要介绍它们之间的关系:
1.Widget
Widget是Flutter应用中的基础构建块,是一个配置的描述,它定义了应用程序的UI部分,例如文本、行、列等。Widgets本身并不是UI,它们更像是告诉Flutter框架应该如何构建UI的蓝图。
2.Element
Element是Widget的实例化。当一个Widget被放置到树中时,它会被一个对应的Element所包裹。Element对象是持久的,它保存了Widget树的状态。当Widget的配置发生变化时,Element会比较新旧Widgets,并决定是否需要更新界面。
当框架被要求根据Widget构建UI时,它实际上是在创建Element。每个Widget都对应一个Element。Element是Widgets的实例化,它们在树结构中持有位置,并负责管理Widgets的生命周期。
3.RenderObject
RenderObject是负责具体的绘制操作的对象。它知道如何在屏幕上渲染自己,处理布局和大小调整。每个Element都会关联一个RenderObject,当Element的状态发生变化时,对应的RenderObject会进行重新绘制。
这是实际负责在屏幕上绘制UI的对象。它们处理布局和绘图逻辑。通常,一个Element会持有一个RenderObject,负责将Element的配置转换成实际的像素渲染在屏幕上。
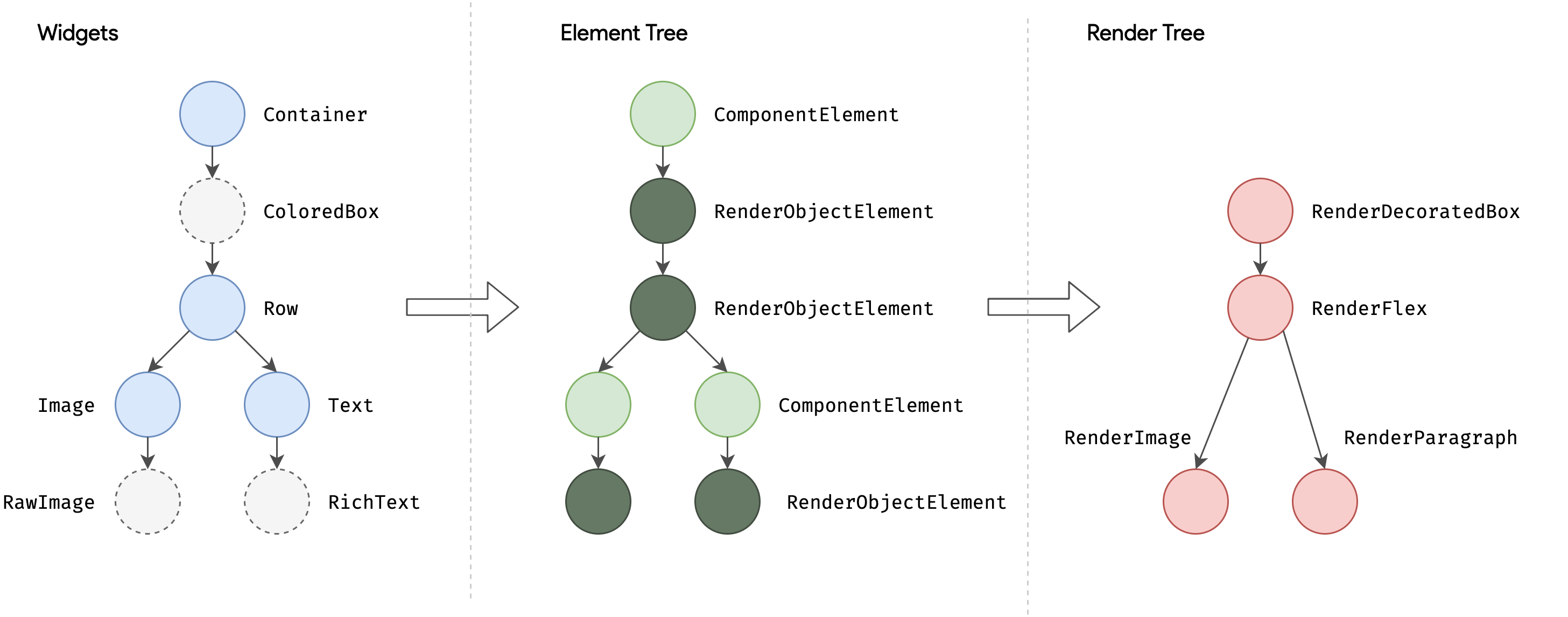
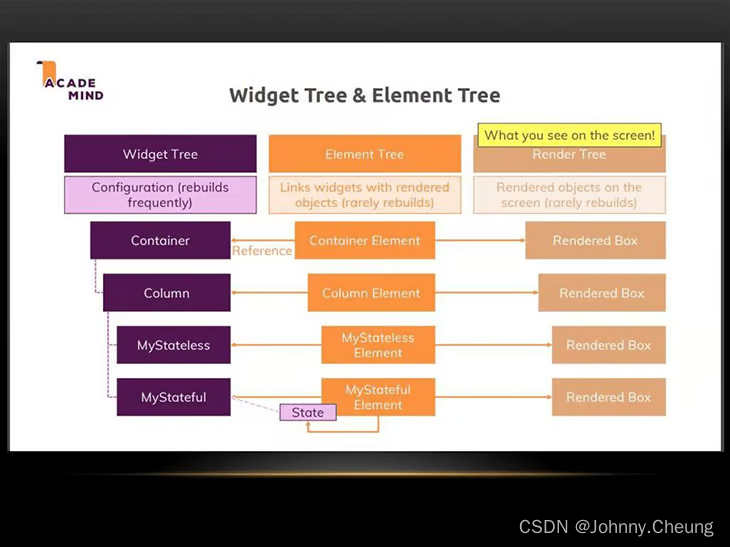
关系流程可以这样理解:你写的Widget通过框架变成Element,Element再根据Widget的配置创建和更新RenderObject。RenderObject最终负责在屏幕上绘制内容。
相关文章:

Flutter的Widget, Element, RenderObject的关系
在Flutter中,Widget,Element和RenderObject是三个核心的概念,它们共同构成了Flutter的渲染流程和组件树的基础。下面简要介绍它们之间的关系: 1.Widget Widget是Flutter应用中的基础构建块,是一个配置的描述…...

测试员练就什么本领可以让自己狂揽10个offer
最近,以前的一个小徒弟又双叒叕跳槽了,也记不清他这是第几次跳槽了,不过从他开始做软件测试开始到现在已经有2-3年的工作经验了,从一开始的工资8K到现在的工资17K,不仅经验上积累的很多,财富上也实现了翻倍…...

vue中实现图片懒加载的几种方法
Vue-lazyload 是一个基于 Vue.js 的图片懒加载库,它的实现原理是基于 Intersection Observer API。Intersection Observer API 是一种异步观察目标元素与其祖先元素或顶级文档视窗交叉状态的方式。 Vue-lazyload 的实现原理如下: 在需要懒加载的图片元素…...
Axure9基本操作
产品经理零基础入门(四)Axure 原型图教程,2小时学会_哔哩哔哩_bilibili Axure 9 从入门到精通全集,自学必备_哔哩哔哩_bilibili 1. ① 页面对应页面个数,概要对应每个页面的具体内容 ② 文件类型 ③ 备用间隔改为5分…...

Docker - 网络
Docker - 网络 理解Docker0 # 我们发现这个容器带来网卡,都是一对对的 # evth-pair 就是一对的虚拟设备接口,他们都是成对出现的,一段连着协议,一段彼此相连 # 正因为有了这个特性,evth-pair 充当一个桥梁࿰…...

vue、react中虚拟的dom
React中虚拟DOM的例子: 下面是一个使用React创建的简单的计数器组件: import React, { Component } from react;class Counter extends Component {constructor(props) {super(props);this.state {count: 0};}handleClick () > {this.setState({c…...
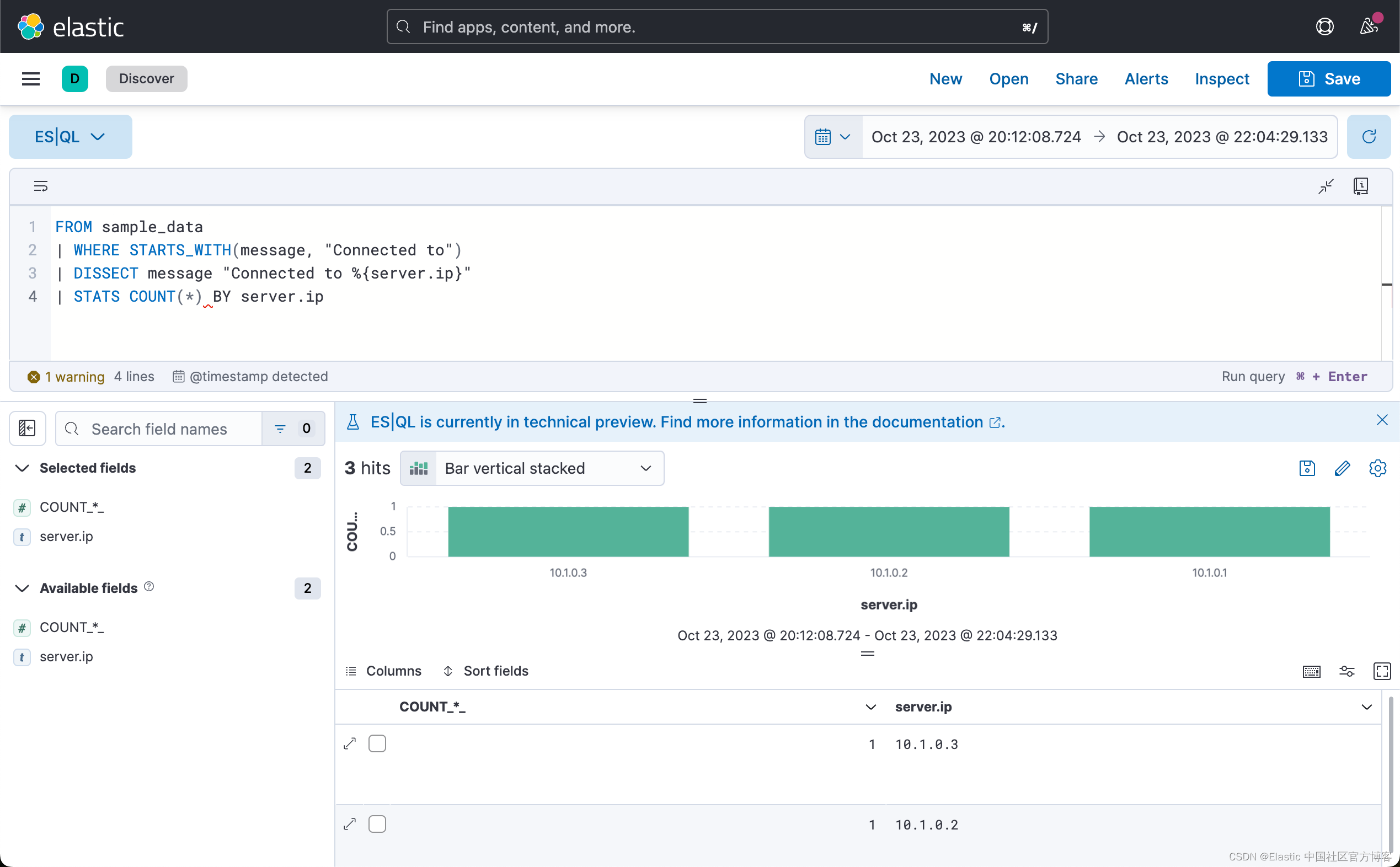
Elasticsearch:ES|QL 快速入门
警告:此功能处于技术预览阶段,可能会在未来版本中更改或删除。 Elastic 将努力解决任何问题,但技术预览版中的功能不受官方 GA 功能的支持 SLA 的约束。目前的最新发行版为 Elastic Stack 8.11。 Elasticsearch 查询语言 (ES|QL) 提供了一种强…...

7-1 进步排行榜
7-1 进步排行榜 分数 10 作者 黄龙军 单位 绍兴文理学院 假设每个学生信息包括“用户名”、“进步总数”和“解题总数”。解题进步排行榜中,按“进步总数”及“解题总数”生成排行榜。要求先输入n个学生的信息;然后按“进步总数”降序排列;若…...
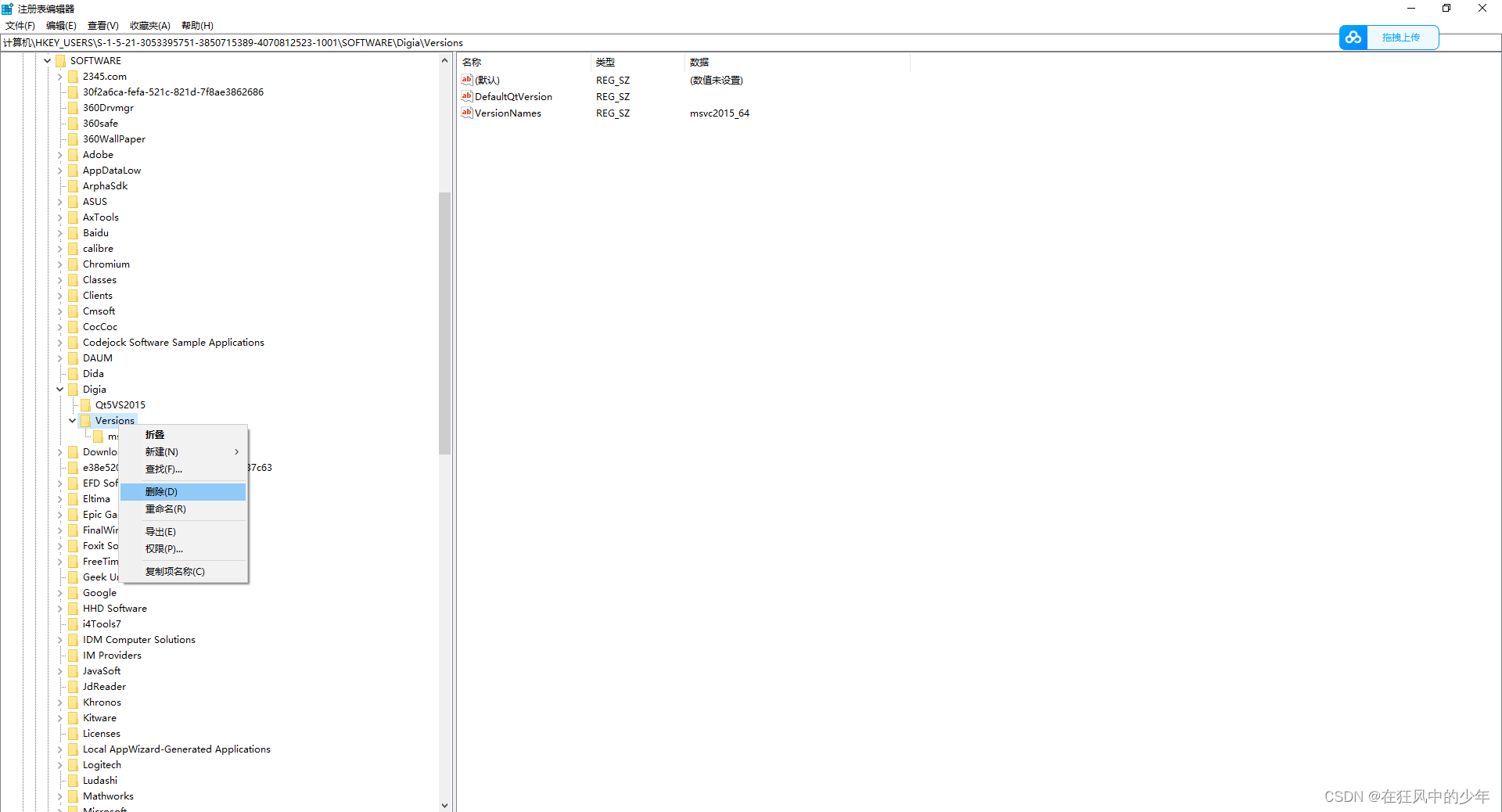
解决删除QT后Qt VS Tools中Qt Options中未删除的错误
在Qt VS Tools的Qt Options已经配置好Qt Versions后如果删除QT程序之后会出现Default Qt/Win version任然存在,这是如果再添加一个话就不能出现重名了,如果新建一个其他名字的话其实在vs中还是不能正常运行qt,会出现点击ui文件vs会无故重启或…...
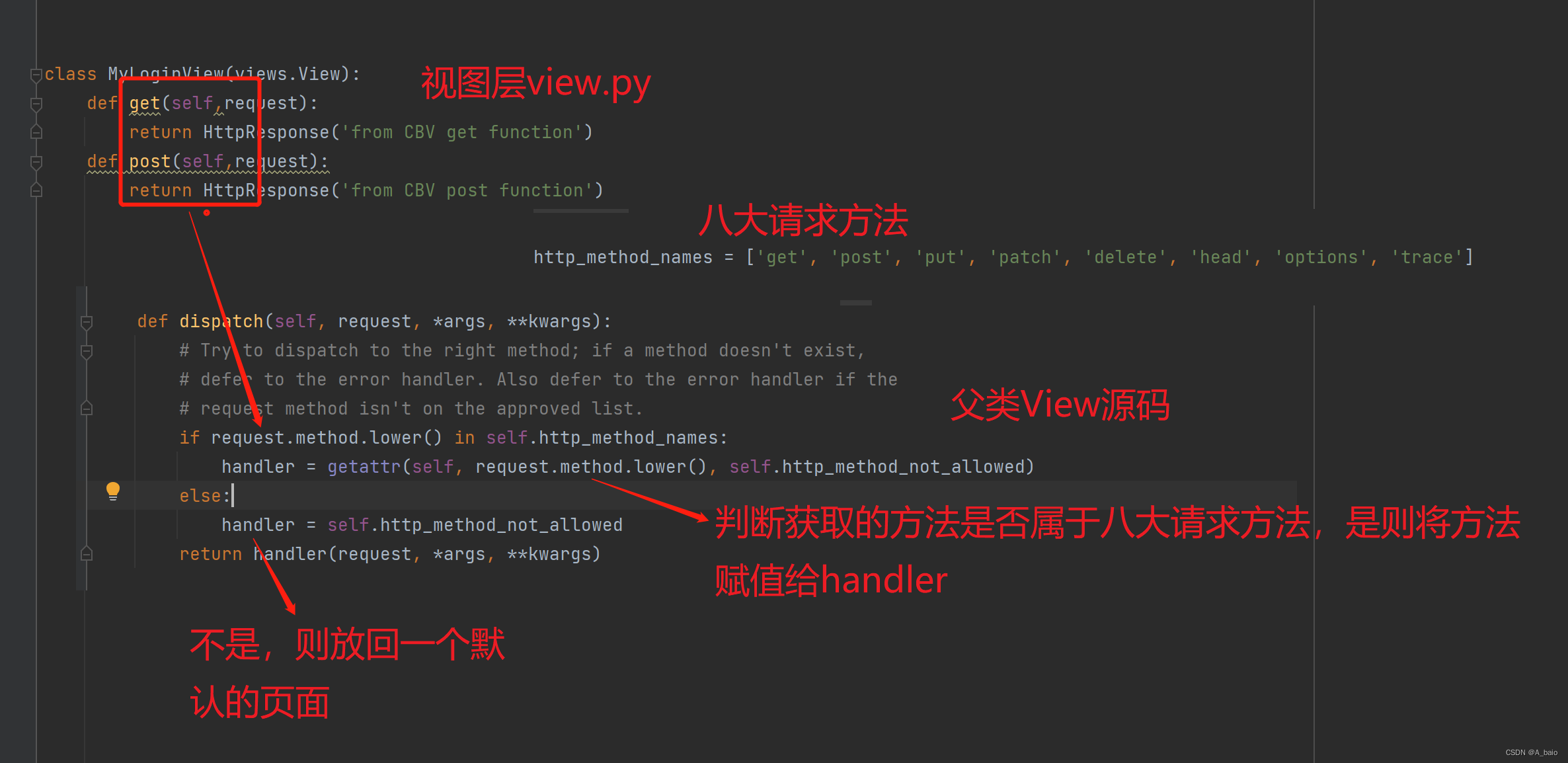
Django(五、视图层)
文章目录 一、视图层1.视图函数返回值的问题2.三板斧的使用结论:在视图文件中写视图函数的时候不能没有返回值,默认返回的是None,但是页面上会报错,用来处理请求的视图函数都必须返回httpResponse对象。 二、JsonReponse序列化类的…...
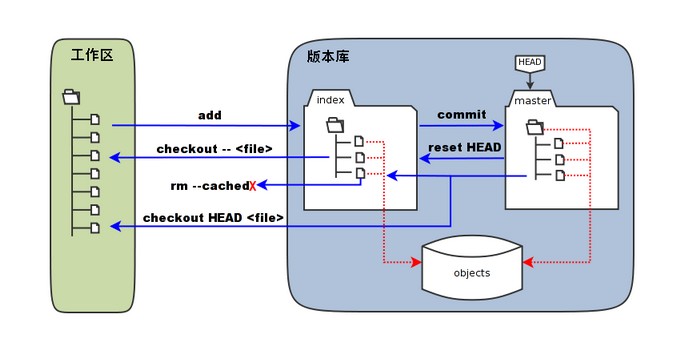
Git 工作流程、工作区、暂存区和版本库
目录 Git 工作流程 Git 工作区、暂存区和版本库 基本概念 Git 工作流程 本章节我们将为大家介绍 Git 的工作流程。 一般工作流程如下: 克隆 Git 资源作为工作目录。在克隆的资源上添加或修改文件。 如果其他人修改了,你可以更新资源。在提交前查看…...

PLSQL使用技巧
欲善其事,必先利其器,最近研究了一下各种编程工具的使用,发掘了不少新功能,能够大大提升我们日常的工作效率,下面是转载的一篇PLSQL使用技巧,个人感觉很有用,分享一下。 1、PL/SQL Developer记…...

DEC 深度编码聚类函数
2. 辅助目标函数 要使用输入 (bt, groups, embed_dim) 计算 DEC 模型的目标分布,关键部分是使用软分配 q ,其形状为 (bt, groups, max_cluster) 。这里, max_cluster 是您要定位的集群数量。当您沿该维度执行聚类时,需要跨 group…...
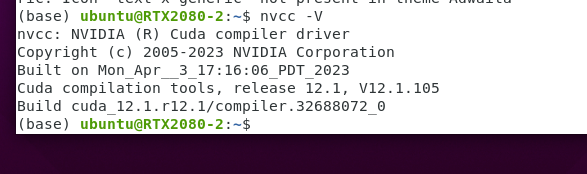
ubuntu中cuda12.1配置(之前存在11.1版本的cuda)(同时配置两个版本)
ubuntu中cuda12.1配置 由于YOLOv8项目中Pytorch版本需要cuda12.1版本 在官网下载12.1版本的deb包 官网地址 sudo dpkg -i cuda-keyring_1.0-1_all.deb sudo apt-get update sudo apt-get -y install cuda然后需要修改bashrc文件(隐藏文件) 添加 exp…...
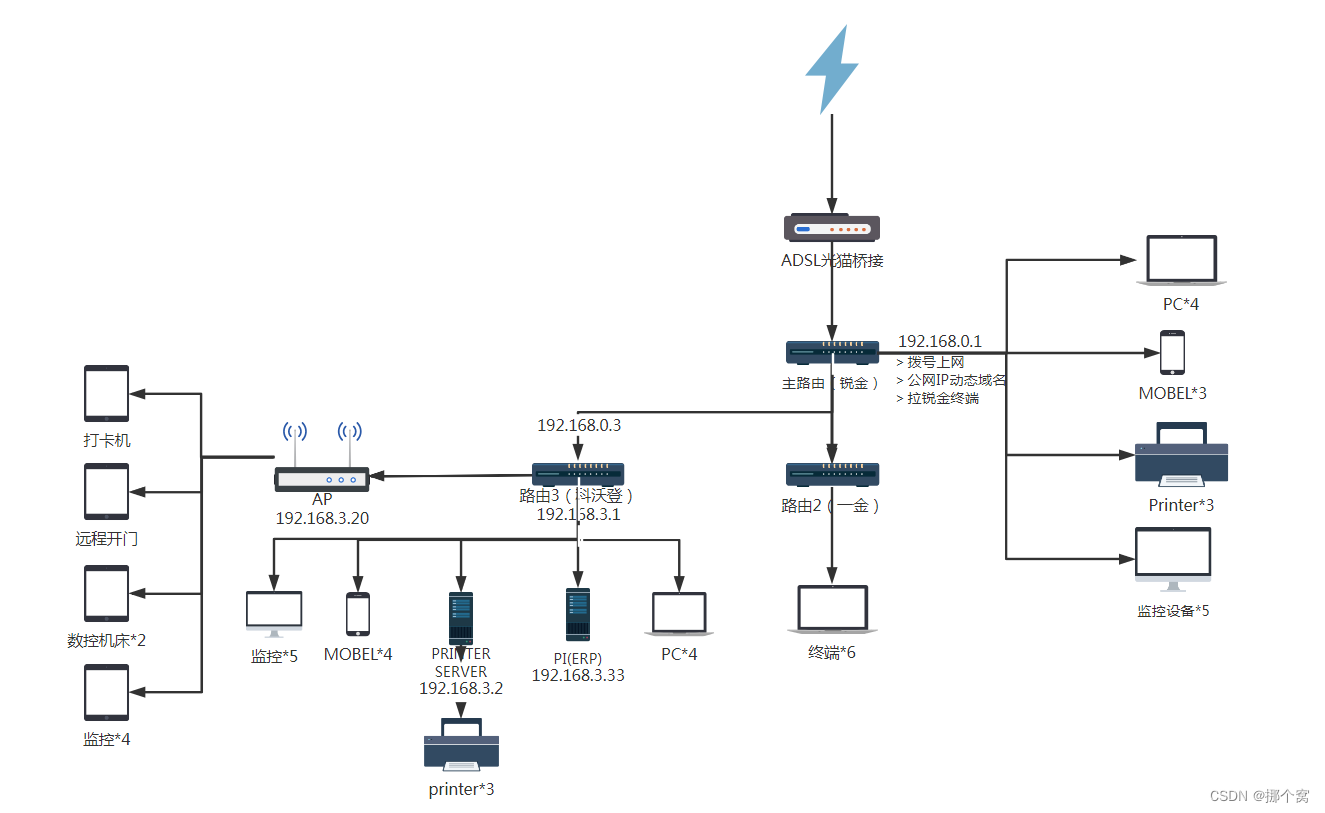
千兆路由只有200M,原来是模式选择不对,也找到了内网不能通过动态域名访问内部服务的原因
本来1000M的宽带接入的,但是一测试发现只有200M,把电信叼了过来, 一测试发现宽带没问题,网线正常,网卡正常,只有可能是路由器的问题了,尴尬了,赶紧给满意好评放他走。回头好好研究一…...

【10】maven打包报错 spring-boot-maven-plugin 与spring-boot 版本的不一致
报错信息 org/springframework/boot/maven/RepackageMojo has been compiled by a more recent version of the Java Runtime (class file version 61.0), this version of the Java Runtime only recognizes class file versions up to 52.0 解决方法 是因为pring-boot-mav…...

SQLAlchemy 在 Flask 应用中的使用和最佳实践
SQLAlchemy 在 Flask 应用中的使用和最佳实践 [TOC](SQLAlchemy 在 Flask 应用中的使用和最佳实践) 模型的编写**SQLAlchemy 中建立关联****利用 SQLAlchemy 中的关联进行查询****实现示例** backref与back_populates?**backref反向引用****back_populates后填充** …...
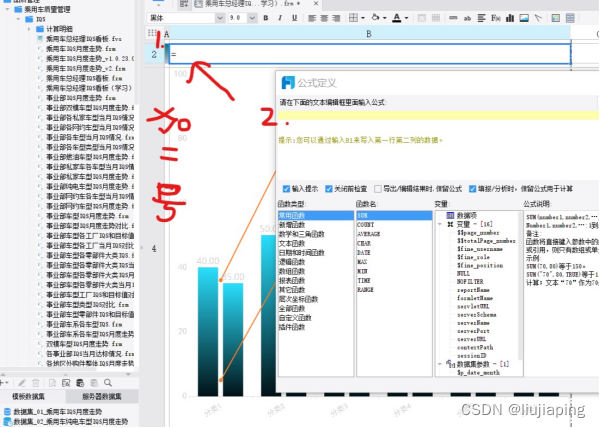
FineReport -问题学习图表设计图表类型-单元格扩展父子格-报表预览
1,问:为什么本地每次预览都要填帐号密码?答:模板认证关闭一下及可 2.单元格扩展与父子格----左父格-扩展方向-箭头往那个方向就往那个方向 1)数据集参数 在定义数据集时,通过使用if函数判断参数的值是否为空,若为空就不过滤参数,若不为空就进行参数过滤。SELECT * FROM…...
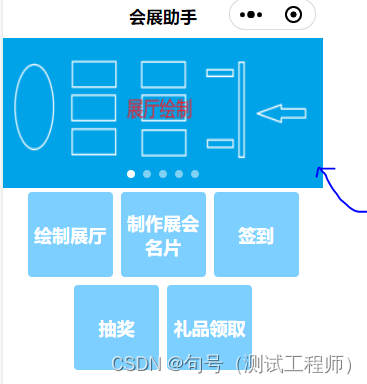
微信小程序广告banner、滚动屏怎么做?
使用滑块视图容器swiper和swiper-item可以制作滚动屏,代码如下: wxml: <swiper indicator-dots indicator-color"rgba(255,255,255,0.5)" indicator-active-color"white" autoplay interval"3000"><swiper-ite…...

Network(一)计算机网络介绍
一 计算机网络 1 概述 什么是计算机网络? 硬件方面:通过线缆将网络设备和计算机连接起来 软件方面:操作系统,应用软件,应用程序通过通信线路互连 实现资源共享、信息传递、增加可靠性、提高系统处理能力 2 网络与云计算 3 计算机网…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
