算法学习打卡day45|动态规划:股票问题总结
Leetcode股票问题总结篇
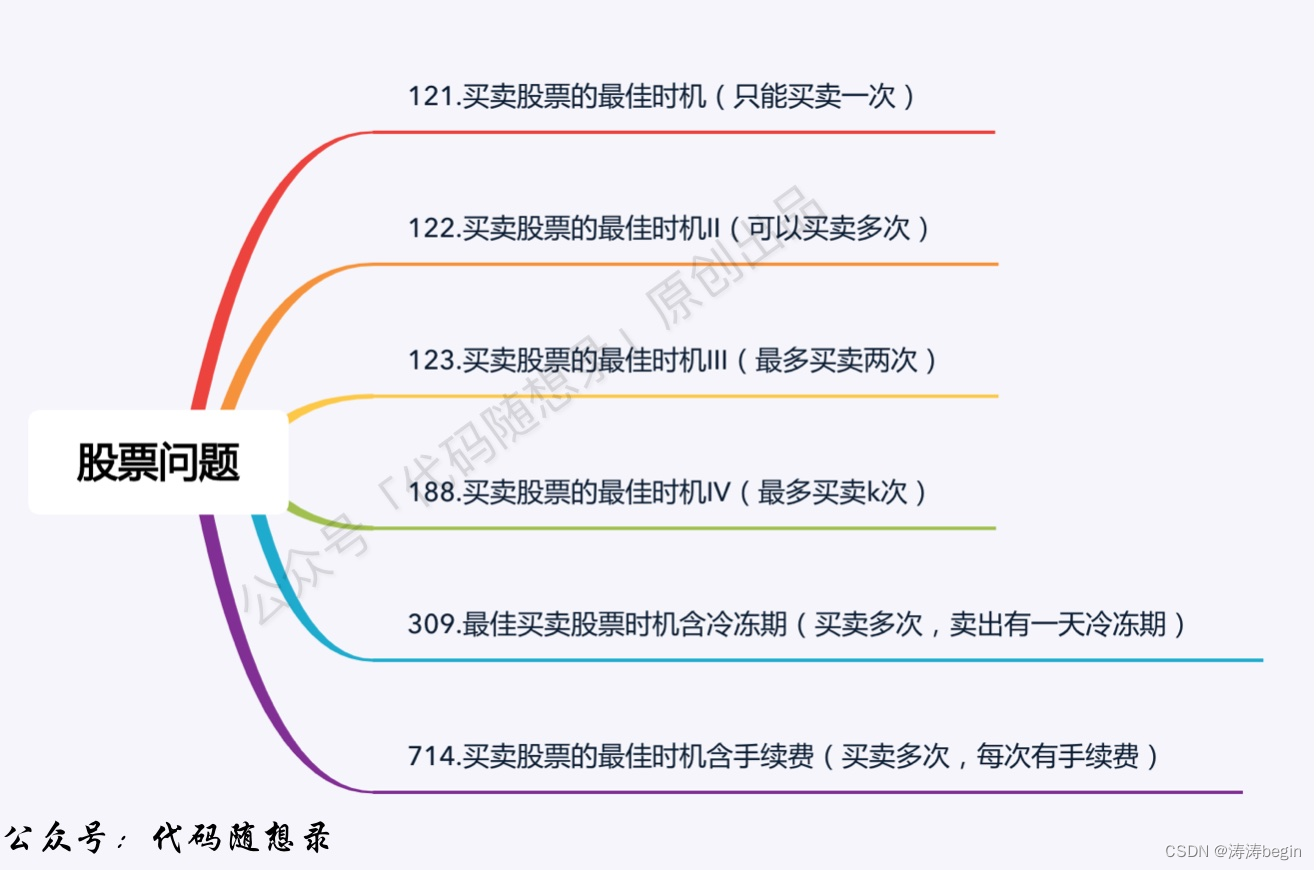
- 动态规划的股票问题一共六道题,买卖股票最佳时机和买卖股票手续费都是一个类型的问题,维护好买入和卖出两个状态即可,方法一摸一样。而冷冻期也差不多就是状态多了点,买入、保持卖出、当日卖出、以及冷冻期四个状态。
- 做题方法还是动态规划五部曲:
- 明确dp数组含义,这里六道题全部第i天都是手里买入状态或者卖出状态的现金数是多少,这篇文章下标0代表未持有,下标1代表持有。
- 写出递推公式,下面写了最基本的,其他题的公式都是在这个基础上做了修改的:
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = max(dp[i - 1][1], -prices[i]);- 最佳时机2那道题就是在这个基础上,修改买入时的递推公式为
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0]-prices[i - 1]); - 最佳时机3那道题是增加两个状态表示第二次买入和卖出:
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]); - 最佳时机4那道题是增加到2 * k个状态,那么内层就要变为双层循环为各个状态赋值了。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] + prices[i]); - 冻结期那道题的递推公式就稍微复杂了,需要维护四个状态,分别是买入、保持卖出、当日卖出、以及冷冻期。
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);dp[i][2] = dp[i - 1][0] + prices[i];dp[i][3] = dp[i - 1][2]; - 含手续费这道题和第二道题一摸一样,在卖出时减去手续费就行。
- 最佳时机2那道题就是在这个基础上,修改买入时的递推公式为
- 初始化:每次买入的时候必须初始化为-price[0],其他赋值为0即可。
- 遍历顺序:由于需要用到 i - 1的资金,所以从前往后遍历
121. 买卖股票的最佳时机
力扣题目链接
代码实现:
int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size() + 1, vector(2, 0));dp[1][0] = 0, dp[1][1] = -prices[0];//二维数组0代表不持有,1代表持有for (int i = 2; i <= prices.size(); ++i) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i - 1]);dp[i][1] = max(dp[i - 1][1], -prices[i - 1]);}return dp[prices.size()][0];}
- 动态规划二维数组滚动数组优化方式:
int maxProfit(vector<int>& prices) {vector<vector<int>> dp(2, vector(2, 0));//只记录当前天和前一天的状态即可dp[0][0] = 0, dp[0][1] = -prices[0];//二维数组0代表不持有,1代表持有for (int i = 1; i < prices.size(); ++i) {dp[i % 2][0] = max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] + prices[i]);dp[i % 2][1] = max(dp[(i - 1) % 2][1], -prices[i]);//看实现通过求余,每次取的都是前一个元素值}return dp[(prices.size() + 1) % 2][0];//用+1,因为数组可能为空}
- 动态规划一维数组实现法,比二维实现更简洁
int maxProfit(vector<int>& prices) {vector<int> dp(2, 0);//只记录当前天的状态即可dp[0] = 0, dp[1] = -prices[0];//0代表不持有,1代表持有for (int i = 1; i < prices.size(); ++i) {dp[0] = max(dp[0], dp[1] + prices[i]);dp[1] = max(dp[1], -prices[i]);}return dp[0];}
- 贪心法实现(每次更新左边界为最小值,然后不断更新result结果):
int maxProfit(vector<int>& prices) {int low = INT_MAX, result = 0;for (int i = 0; i < prices.size(); ++i) {low = min(low, prices[i]);result = max(result, prices[i] - low);}return result;}
买卖股票的最佳时机2
力扣题目链接
思路:
- 在上题基础上增加了买卖次数,修改买入时的计算方法即可。
代码实现
- 普通动态规划想法,直接计算每天的利润(和贪心类似)
int maxProfit(vector<int>& prices) {//dp[i] = max(dp[i - 1], dp[i - 1] + prices[i] - prices[i - 1]);vector<int> dp(prices.size(), 0);for (int i = 1; i < prices.size(); ++i) {dp[i] = max(dp[i - 1], dp[i - 1] + prices[i] - prices[i - 1]);} return dp[prices.size() - 1];}
- 用双状态实现的方法(这里用一维数组实现的,也可以是二维)
int maxProfit(vector<int>& prices) {vector<int> dp(2, 0);dp[0] = 0, dp[1] = -prices[0];for (int i = 1; i < prices.size(); ++i) {dp[0] = max(dp[0], dp[1] + prices[i]);dp[1] = max(dp[1], dp[0] - prices[i]);}return dp[0];}
- 贪心法
int maxProfit(vector<int>& prices) {int profit = 0;for (int i = 1; i < prices.size(); i++) {profit += max(prices[i] - prices[i - 1], 0);}return profit;}
- 双指针法
int maxProfit(vector<int>& prices) {int profit = 0, buy_index = 0;for (int i = 0; i < prices.size() - 1; i++) {if (prices[i] > prices[i + 1]) {profit += prices[i] - prices[buy_index];buy_index = i + 1;continue;}if (i + 1 == prices.size() - 1) {profit += prices[i + 1] - prices[buy_index];}}return profit;}
买卖股票的最佳时机3
力扣题目链接
思路:
- 这道题规定只能买卖两次,实现方法上面已经写过了,直接上代码
代码实现
int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(), vector<int>(5, 0));dp[0][1] = -prices[0], dp[0][3] = -prices[0];//相当于当天买卖一次后再次买入for (int i = 1; i < prices.size(); ++i) {dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[prices.size() - 1][4];}
买卖股票的最佳时机4
力扣题目链接
思路:
买卖次数规定为k次,需要利用循环给每次买卖赋值。
代码实现
int maxProfit(int k, vector<int>& prices) {vector<vector<int>> dp(prices.size(), vector<int>(k * 2 + 1, 0));for (int i = 1; i < 2 * k + 1; i += 2) {dp[0][i] = -prices[0];}for (int i = 1; i < prices.size(); ++i) {for (int j = 1; j <= 2 * k - 1; j += 2) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] + prices[i]);}}return dp[prices.size() - 1][2 * k];}
买卖股票的最佳时机含冷冻期
力扣题目链接
题目描述:
在第二题基础上,增加了冷冻期,需要维护四个状态
代码实现
int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(len, vector<int>(4, 0));dp[0][0] = -prices[0];for (int i = 1; i < len; ++i) {dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);dp[i][2] = dp[i - 1][0] + prices[i];dp[i][3] = dp[i - 1][2];}return max(dp[len - 1][1], max(dp[len - 1][2], dp[len - 1][3]));}
买卖股票的最佳时机含手续费
力扣题目链接
题目描述:
和第二题基本一样,卖出时减去手续费就行了
代码实现
int maxProfit(vector<int>& prices, int fee) {vector<vector<int>> dp(prices.size(), vector<int>(2, 0));dp[0][1] = -prices[0];for (int i = 1; i < prices.size(); ++i) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);}return dp[prices.size() - 1][0];}
相关文章:

算法学习打卡day45|动态规划:股票问题总结
Leetcode股票问题总结篇 动态规划的股票问题一共六道题,买卖股票最佳时机和买卖股票手续费都是一个类型的问题,维护好买入和卖出两个状态即可,方法一摸一样。而冷冻期也差不多就是状态多了点,买入、保持卖出、当日卖出、以及冷冻期…...

内网环境下让容器上网,并制作一个httpd容器
1.下载基础镜像 上一次,我们通过正向互联网代理在内网环境中,搭建了一个docker环境,具体环境如下: 1) 内网docker服务器:192.168.123.1,操作系统为:redhat 7.9 2) 代理服务器(可通外网)&#…...

多个Obj模型合并
MergeObj(合并Obj模型) 1 概述 由于项目原因,需要下载谷歌地图上的模型,关于谷歌模型下载的,见我的CSDN博客. 由于下载谷歌地图上的数据,会分多个模块下载。下载完成后,怎么合并,在…...

Qt调用python写好的函数,利用Python丰富的图像处理库来完成各种任务
一、前言 近年来,Python已经成为一种广泛应用于科学计算、数据分析和机器学习等领域的强大编程语言。其丰富的生态系统和大量的开源库使得Python成为处理图像、音频、视频和其他多媒体数据的理想选择。在图像处理领域,Python提供了许多方便的函数和库,如OpenCV、PIL(Pytho…...

第六章:接口
系列文章目录 文章目录 系列文章目录前言一、接口二、实现接口与继承类三、接口的多态特性总结 前言 接口是更加抽象的类。 一、接口 usb插槽就是现实中的接口,厂家都遵守了统一的规定包括尺寸,排线等。这样的设计在java编程中也是大量存在的。 packa…...

【Java 进阶篇】JQuery DOM操作:CRUD操作的前端魔法
在前端开发的舞台上,CRUD(Create, Read, Update, Delete)操作是一种极为重要的技能,它涉及对页面元素的增删改查。而JQuery,这位前端开发的魔法师,为我们提供了便捷而强大的方法,使得CRUD操作变…...
如何实现Redisson分布式锁
首先,不要将分布式锁想的太复杂,如果我们只是平时业务中去使用,其实不算难,但是很多人写的文章不能让人快速上手,接下来,一起看下Redisson分布式锁的快速实现 Redisson 是一个在 Redis 的基础上实现的 Java…...
Kafka(三)生产者发送消息
文章目录 生产者发送思路自定义序列化类配置生产者参数提升吞吐量 发送消息关闭生产者结语示例源码仓库 生产者发送思路 如何确保消息格式正确的前提下最终一定能发送到Kafka? 这里的实现思路是 ack使用默认的all开启重试在一定时间内重试不成功,则入库ÿ…...

2020年五一杯数学建模C题饲料混合加工问题解题全过程文档及程序
2020年五一杯数学建模 C题 饲料混合加工问题 原题再现 饲料加工厂需要加工一批动物能量饲料。饲料加工需要原料,如加工猪饲料需要玉米、荞麦、稻谷等。加工厂从不同的产区收购了原料,原料在收购的过程中由于运输、保鲜以及产品本身属性等原因ÿ…...

公益SRC实战|SQL注入漏洞攻略
目录 一、信息收集 二、实战演示 三、使用sqlmap进行验证 四、总结 一、信息收集 1.查找带有ID传参的网站(可以查找sql注入漏洞) inurl:asp idxx 2.查找网站后台(多数有登陆框,可以查找弱口令,暴力破解等漏洞&…...
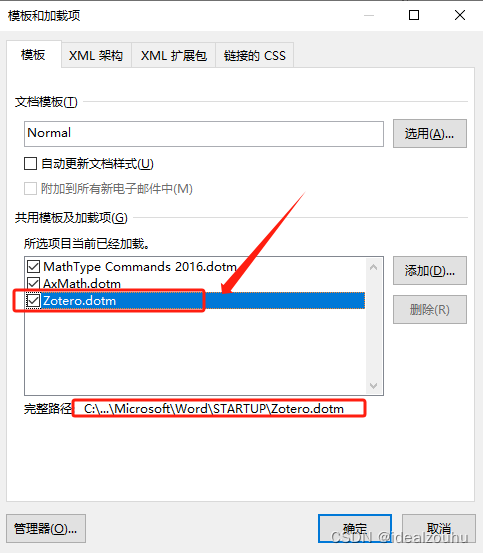
Word软件手动安装Zotero插件
文章目录 Word软件手动安装Zotero插件方法一方法二 参考资料 Word软件手动安装Zotero插件 方法一 关闭word在zotero中依次点击编辑—首选项—引用—文字编辑软件—重新安装加载项Microsoft word 方法二 寻找Zotero.dotm存储位置, 例如D:\Program Files\Zotero\ext…...
idea 插件推荐第二期
文章目录 便捷开发CodeGlance Pro (代码缩略图)GenerateAllSetter(快速生成对象所有set方法)GsonFormatPlus:json转实体RestfulToolkitX(找到controller快捷请求接口) 美化activate-power-mode-x (敲击计数、动效)Nyan…...

plsql查询中文出现乱码
添加环境变量:如下 变量名:NLS_LANG 变量值:SIMPLIFIED CHINESE_CHINA.ZHS16GBK 变量名:TNS_ADMIN 变量值:D:\instantclient_11_2\network\admin 在Path中添加instantclient_11_2存放路径...

【Docker】五分钟完成Docker部署Java应用,你也可以的!!!
文章目录 前言一、部署步骤1.项目结构2.Dockerfile3.docker-compose.yml4.启动5.常用命令 总结 前言 本文基于Docker Compose部署Java应用,请确保你已经安装了Docker和Docker Compose。 十分钟就能上手docker?要不你也试试? 一、部署步骤 1…...
如何准备2024年的系统设计面试?
1 前言 如果你正在准备软件工程师或软件开发人员的面试,那么你可能知道由于其开放性质和广泛性,准备系统设计是多么困难,但同时你也不能忽略它。在软件工程界,如果你正在申请高级工程师/主管/架构师或更高级别的角色,系统设计是最受追捧的技能,也是整个过程中最重要的环节之一…...

【开源】基于JAVA的电子元器件管理系统
目录 一、摘要1.1 项目简介1.2 项目详细录屏 二、研究内容三、界面展示3.1 登录&注册&主页3.2 元器件单位模块3.3 元器件仓库模块3.4 元器件供应商模块3.5 元器件品类模块3.6 元器件明细模块3.7 元器件类型模块3.8 元器件采购模块3.9 元器件领用模块3.10 系统基础模块 …...
足底筋膜炎怎么治疗治愈
足底筋膜炎又称为跖筋膜炎,跖筋膜主要在足弓下方,它维持足弓稳定性,对于喜欢长期长跑、跳远,或者越野运动,或者部队中的士兵进行拉练,还有需要久坐或者久站的人群中,容易发生跖筋膜炎。治疗方法…...

Keil工程忽略文件.gitignore、自动删除脚本:keilkilll.bat、自动生成目录文件列表脚本
Keil工程忽略文件:.gitignore 忽略规则 *.rar *.o *.d *.crf *.htm *.dep *.map *.bak *.lnp *.lst *.ini *.iex *.sct *.scvd *.dbg* *.uvguix.* *Log.*#忽略.gitignore根目录下的文件夹,根据自己的需要修改 RTE/ Templates/ Examples/ OBJ/#不能忽略…...

软考高级职称哪个好考?明确给你答案
软考考试分为初、中、高三级,其中高级5个方向分别为系统分析师、信息系统项目管理师、网络规划设计师、系统架构设计师、系统规划与管理师。软考高级职称考什么好?有很多人是因为要评高级职称而选择参考软考高级资格考试,那么软考高级里哪个资…...

智能客服外包服务适用于哪些行业?
在当今快节奏的商业环境下,企业需要更高效、更智能且更灵活的客户服务解决方案。而智能客服外包服务正是满足这一需求的利器。不仅可以帮助企业提升客户服务的品质和效率,还能降低企业的运营成本。智能客服外包服务适用于哪些行业呢? 1.电子…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
