<蓝桥杯软件赛>零基础备赛20周--第5周--杂题-2
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周(读者可以按自己的进度选“正常”和“快进”两种计划)。
每周3次集中答疑,周三、周五、周日晚上,在QQ群上答疑:

文章目录
- 0. 上周答疑
- 1. 精讲题
- 1.1 修剪灌木
- 1.2 英文数字计数
- 1.3 矩形拼接
- 1.4 最少砝码
- 1.5 蜂巢
- 1.6 立方体表面距离
- 2. 刷题
第 4周: 杂题-2
0. 上周答疑
伪代码怎么转化Java语言?
C/C++、Java、Python代码怎么互转?
回答:用大数据模型转,例如文心一言3.5,是免费的。
在转换代码这件事上,大数据模型做得很好。
1. 精讲题
本周还是杂题!
大家是不是感到太慢了,什么时候才学数据结构、算法呢?我想立刻现在马上学:二分、排序、二叉树、DFS、…
不要着急,杂题做得越多,后面的学习越高效越快!
一是提高编码能力!争取做到:一次写20行代码,不用调试一次过!
二是算法能力!杂题虽然没用到经典算法,但它们的解题步骤其实也是算法,有时难度不亚于经典算法。
下面给出6个精讲题,有模拟、构造、思维、数学等各种杂题,难度从简单到难。大家自己先做,然后再看题解。
1.1 修剪灌木
难度 **
2022年第十三届省赛:链接1-蓝桥OJ 、链接2-NewOj
【题解】这是一道思维题。由于每棵灌木都会在2N天内被剪为0,所以不会无限长高。其中的第i棵,它左边有i-1棵,右边有n-i棵。爱丽丝分别从左右绕回来,各需要2i和2(n-i-1)天,取最大值就是高度。i从0开始。
(1)C/C++代码
#include<bits/stdc++.h>
using namespace std;
int main() {int n; cin >> n;for (int i = 0; i < n; i++) cout << max(i, n - i - 1) * 2 << endl;return 0;
}
(2)python代码
n = int(input())
for i in range (n): print(max(i,n-i-1)*2)
(3)java代码
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();for (int i = 0; i < n; i++) {System.out.println(Math.max(i, n - i - 1) * 2);}}
}
1.2 英文数字计数
见博客:英文数字计数
难度 ***
1.3 矩形拼接
2022年第十三届省赛: 链接-NewOJ
难度 *** 准确地说,难度有3.5颗星
【题解】本题是一道纯粹的构造题,思维简单,但是代码比较繁琐细致,目的是考核编码能力。
3个矩形摆在一起,可能有几个边?读者可以在纸上手画观察,如果3个矩形完全不能匹配,是8边形;如果能完全匹配成一个新矩形,是4边形;其他情况是6边形。
本题只有3个矩形,并不复杂。3个矩形做任意组合,每个矩形有横竖两种摆法,共48种情况。T = 1000组测试,总计算量是1000×48,计算量很小不会超时,所以简单地用暴力法组合出所有情况,取最小值即可。
(1)C/C++代码
下面的C++代码,第10 ~ 14行,对3个矩形进行组合。第15 ~ 17行,每个矩形有横和竖两种摆法。
第18行,如果一个矩形的边长等于另外两个矩形边长之和,那么至少是6个边。然后第20行,如果这两个矩形边长相等,那么就是4个边。后面几行请自己分析。
#include<bits/stdc++.h>
using namespace std;
int a[3][2];
int main(){int T; cin >> T;while(T--) {for(int i = 0; i < 3; i++)cin >> a[i][0] >> a[i][1];int ans = 8;for(int i = 0; i < 3; i++) //第1个矩形for(int j = 0; j < 3; j++)if(i != j) //第2个矩形for(int k = 0; k < 3; k++)if(k != i && k != j) //第3个矩形for(int ii = 0; ii <= 1; ii++){ //第1个有横竖两种摆法for(int jj = 0; jj <= 1; jj++){ //第2个横竖摆for(int kk = 0; kk <= 1; kk++){ //第3个横竖摆if(a[i][ii] == a[j][jj] + a[k][kk]){ ans = min(ans, 6);if(a[j][1-jj] == a[k][1-kk])ans = min(ans, 4);}if(a[i][ii] == a[j][jj] || a[j][jj] == a[k][kk])ans = min(ans, 6);if(a[i][ii] == a[j][jj] && a[j][jj] == a[k][kk])ans = min(ans, 4);}}}cout<<ans<<endl;}return 0;
}
(2)python代码
def check1(x1,x2,x3):if x1>=x2 and x1>=x3:if x1==x2+x3 and a[2]+a[3]-x2==a[4]+a[5]-x3: return Trueif x2>=x1 and x2>=x3:if x2==x1+x3 and a[0]+a[1]-x1==a[4]+a[5]-x3: return Trueif x3>=x1 and x3>=x2:if x3==x1+x2 and a[0]+a[1]-x1==a[2]+a[3]-x2: return Truereturn False
def check2(x1,x2,x3):if x1>=x2 and x1>=x3:if x1==x2+x3: return Trueif x2>=x1 and x2>=x3:if x2==x1+x3: return Trueif x3>=x1 and x3>=x2:if x3==x1+x2: return Truereturn FalseT = int(input())
for t in range(T):a=list(map(int,input().split()))ans=8for i in range(0,2): #第1个矩形for j in range(2,4): #第2个矩形for k in range(4,6): #第3个矩形x1,x2,x3 = a[i],a[j],a[k]if x1==x2 and x2==x3: ans = min(ans,4)if check1(x1,x2,x3): ans = min(ans,4)if x1==x2 or x1==x3 or x2==x3: ans = min(ans,6)if check2(x1,x2,x3): ans = min(ans,6)print(ans)
(3)java代码
import java.util.*;
import java.io.*;
public class Main { public static void main(String[] args) {Scanner in = new Scanner(System.in);int T = in.nextInt();for(int _t = 1; _t <= T; _t++){int[][] a = new int[3][2];int ans = 8;for(int i = 0; i < 3; i++) {a[i][0] = in.nextInt();a[i][1] = in.nextInt();}//枚举第一个矩形下标为i,第二个矩形下标为j,第三个矩形下标为kfor(int i = 0; i < 3; i++)for(int j = 0; j < 3; j++)if(i != j)for(int k = 0; k < 3; k++)if(i != k && j != k)//枚举三个矩形的两条边for(int ii = 0; ii <= 1; ii++)for(int jj = 0; jj <= 1; jj++)for(int kk = 0; kk <= 1; kk++) {if(a[i][ii] == a[j][jj])//6条边的情况1ans = Math.min(ans, 6);if(a[i][ii] == a[j][jj] && a[i][ii] == a[k][kk])//4条边的情况1ans = Math.min(ans, 4);//枚举仅考虑a[i][ii] 与 a[j][jj] + a[k][kk]的关系if(a[i][ii] == a[j][jj] + a[k][kk]) {ans = Math.min(ans, 6); //6条边的情况2if(a[j][1 - jj] == a[k][1 - kk]) //4条边的情况2ans = Math.min(ans, 4);}}System.out.println(ans);}}
}
1.4 最少砝码
2021年第十二届蓝桥杯省赛: 链接1-蓝桥OJ
难度 ***
【题解】这是一道找规律题。
题目要求给出最少数量的几个整数(砝码),通过加减组合得到1 ~ N的整数。熟悉二进制的都知道,用1、2、4、8、16、…这些2的倍数,可以组合后相加得到任意整数。不过,本题的砝码不仅可以相加,还可以放在天平的两边通过减法得到新的称重。例如N = 3时,砝码可以是{1, 2},也可以是{1, 3}、{2, 3}。
本题的思维有一点难度,读者如果自己提前做了此题,思维过程可能比较繁琐。下面给出一种简洁的推理方法。
设当前砝码称重范围是1 ~ R。加一个砝码w,并且要求不重复加w前已经能得到的称重,那么w将是一个很大的砝码。新的称重范围是:
{1, 2, …, R, w-R, w-R+1,…, w, w+1, w+2, …, w+R}
因为从R到w-R是连续的,所以有w-R = R+1,即w = 2R+1。也就是说,如果当前称重范围是1 ~ R,那么加一个w = 2R+1的砝码,可以扩展到新的称重范围R’= w+R = 3R+1。
下面列表计算,每一行的“原砝码,原称重范围”是上一行的“新砝码,新称重范围”。

这个表格给出了一种最少砝码的实现方式,虽然可能有其他实现方式,但这种实现方式最大程度扩展了新的R’,是一种最优方案。
根据这个表格可以得到计算方法:(1)砝码按3的倍数增长;(2)每加一个砝码,称重范围增长到R’ = 3R+1。
R按3倍增长,这比二进制的倍增还快,当N = 1 0 9 10^9 109时,计算量 l o g 3 N log_3N log3N < l o g 2 N log_2N log2N = 30。
(1)C/C++代码
#include <stdio.h>
int main() {int N;scanf("%d", &N);int R = 1;int cnt = 1;while (R < N) {R = R * 3 + 1;cnt++;}printf("%d", cnt);return 0;
}
(2)python代码
N = int(input())
R = 1
cnt = 1
while R < N:R = R*3 + 1cnt += 1
print(cnt)
(3)java代码
import java.util.*;
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int N = scanner.nextInt();int R = 1;int cnt = 1;while (R < N) {R = R * 3 + 1;cnt++;}System.out.println(cnt);}
}
1.5 蜂巢
2022年第十三届省赛: [链接1-蓝桥OJ]
难度 ****
【题解】本题是一道构造题,考点有两个:坐标转换、距离计算。
蜂巢有6个方向,看起来比较复杂,但实际上走步非常简单,例如样例中从B走到C,C在B的右下方,B只要一直向右向下走,且不超过C的行和列,不管怎么走,一定能以最小步数走到C。
本题的难点是对坐标的处理。如果是简单的直角坐标系,很容易计算。本题是六角形的蜂巢,每个蜂巢的中心点是否能转为直角坐标?把蜂巢的关系用下面的直角坐标表示:

中心点O,对应的6个蜂巢的坐标分别为(-2, 0)、(-1, 1)、(1, 1)、(2, 0)、(1, -1)、(-1, -1),下面代码中用xdir[]、ydir[]表示。
先计算得到起点坐标(x1, y1)、终点坐标(x2, y2)。如何计算起点到终点的步数?由于蜂巢的坐标比较奇怪,不能直接用“曼哈顿距离[ 曼哈顿距离,又称为出租车距离:两点的距离等于x方向上的距离加上y方向上的距离,即|x1-x2| + |y1-y2|。]”计算。读者如果已经做了这一题,可能是用各种复杂的判断来计算的。下面给出一个简单巧妙的方法。
坐标之差的绝对值dx = |x1-x2|,dy = |y1-y2|,有以下结论:
1、若dx ≥ dy,那么最少步数是(dx+dy)/2,即先横着走,再斜着走;
2、若dx < dy,一直斜着走就行,最少步数是dy。
(1)C/C++代码
代码中有一个地方需要注意,即坐标值应该用long long,如果用int会溢出。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll xdir[] = {-2,-1,1,2, 1,-1}; //横向
ll ydir[] = { 0, 1,1,0,-1,-1}; //纵向
void walk(ll d, ll q, ll &x, ll &y){x += xdir[d] * q;y += ydir[d] * q; //引用传参,返回坐标值(x,y)
}
int main(){ll d1,p1,q1,d2,p2,q2;cin>>d1>>p1>>q1>>d2>>p2>>q2;ll x1 = 0, y1 = 0; //计算起点坐标(x1, y1)walk(d1,p1,x1,y1); //先走第1个方向walk((d1 + 2) % 6,q1,x1,y1); //再走第2个方向ll x2 = 0, y2 = 0; //计算终点坐标(x2, y2)walk(d2,p2,x2,y2);walk((d2 + 2) % 6,q2,x2,y2);ll dx = abs(x1 - x2), dy = abs(y1 - y2);if (dx >= dy) cout << (dx+dy)/2; //先横走,再斜着走else cout << dy; //一直斜着走就行了
}
(2)python代码
xdir = [-2,-1,1,2, 1,-1]
ydir = [ 0, 1,1,0,-1,-1]
def walk(d, q,x,y): x += xdir[d]*qy += ydir[d]*qreturn x,y
d1,p1,q1,d2,p2,q2 = map(int,input().split())
x1, y1 = walk(d1,p1,0,0)
x1, y1 = walk((d1 + 2) % 6, q1,x1,y1)
x2, y2 = walk(d2,p2,0,0)
x2, y2 = walk((d2 + 2) % 6, q2,x2,y2)
dx,dy = abs(x1 - x2), abs(y1 - y2);
if (dx >= dy): print((dx+dy)//2) #先横走,再斜着走
else: print(dy) #一直斜着走
(3)java代码
import java.util.*;
public class Main {static long[] xdir = {-2, -1, 1, 2, 1, -1}; //横向static long[] ydir = {0, 1, 1, 0, -1, -1}; //纵向static void walk(int d, long q, long[] pos) {pos[0] += xdir[d] * q;pos[1] += ydir[d] * q;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int d1 = scanner.nextInt();long p1 = scanner.nextLong();long q1 = scanner.nextLong();int d2 = scanner.nextInt();long p2 = scanner.nextLong();long q2 = scanner.nextLong();long[] pos1 = {0, 0};walk(d1, p1, pos1);walk((d1 + 2) % 6, q1, pos1);long[] pos2 = {0, 0};walk(d2, p2, pos2);walk((d2 + 2) % 6, q2, pos2);long dx = Math.abs(pos1[0] - pos2[0]);long dy = Math.abs(pos1[1] - pos2[1]);if (dx >= dy) System.out.println((dx + dy) / 2);else System.out.println(dy); }
}
1.6 立方体表面距离
见博客:立方体表面距离
难度 *****
2. 刷题
还是继续刷题吧。上周的题目链接,大家接着做:
蓝桥题库的模拟题-简单
蓝桥题库的模拟题-中等
蓝桥题库的模拟题-困难
蓝桥题库的枚举题-简单
蓝桥题库的枚举题-中等
蓝桥题库的枚举题-困难
蓝桥题库的递归题
相关文章:

<蓝桥杯软件赛>零基础备赛20周--第5周--杂题-2
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周(读者可以按…...
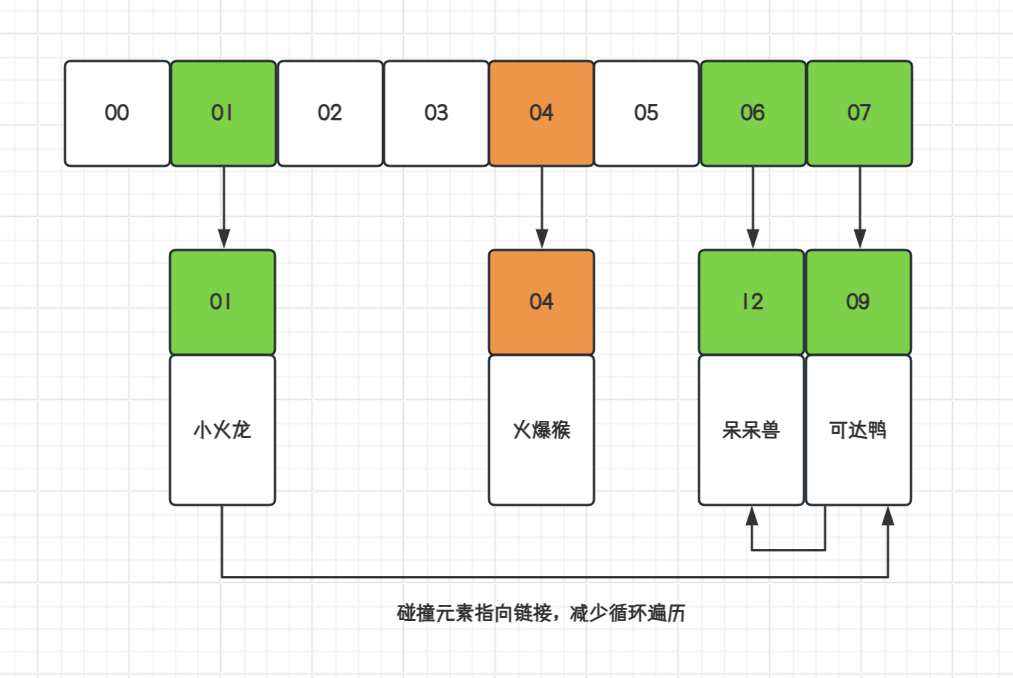
数据结构哈希表(散列)Hash,手写实现(图文推导)
目录 一、介绍 二、哈希数据结构 三、✍️实现哈希散列 1. 哈希碰撞💥 2. 拉链寻址⛓️ 3. 开放寻址⏩ 4. 合并散列 一、介绍 哈希表,也被称为散列表,是一种重要的数据结构。它通过将关键字映射到一个表中的位置来直接访问记录&#…...

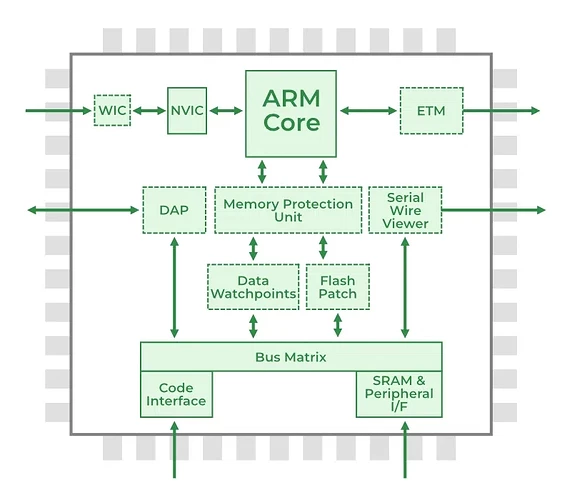
【嵌入式设计】Main Memory:SPM 便签存储器 | 缓存锁定 | 读取 DRAM 内存 | DREM 猝发(Brust)
目录 0x00 便签存储器(Scratchpad memory) 0x01 缓存锁定(Cache lockdown) 0x02 读取 DRAM 内存 0x03 DREM Banking 0x04 DRAM 猝发(DRAM Burst) 0x00 便签存储器(Scratchpad memory&#…...
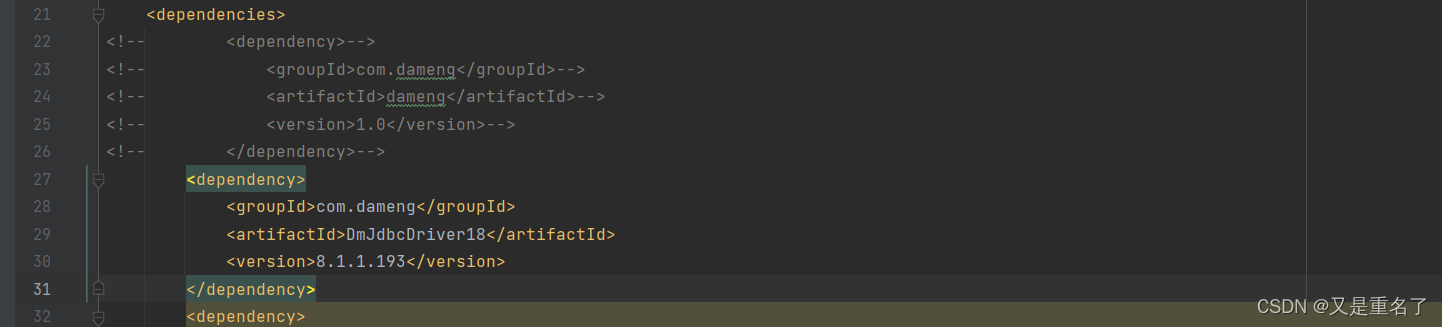
dameng数据库数据id decimal类型,精度丢失
问题处理 这一次也是精度丢失,但是问题呢还是不一样,这一次所有的id都被加一了,只有id字段被加一,还有的查询查出来封装成对象之后对象的id字段被减一了,数据库id字段使用的decimal(20,6)&…...

python图神经网络,注意力机制、Transformer模型、目标检测算法、强化学习等
近年来,伴随着以卷积神经网络(CNN)为代表的深度学习的快速发展,人工智能迈入了第三次发展浪潮,AI技术在各个领域中的应用越来越广泛 本文重点为:注意力机制、Transformer模型(BERT、GPT-1/2/3/…...
安装包 amd,amd64, arm,arm64 都有什么区别
现在的安装包也不省心,有各种版本都不知道怎么选。 根据你安装的环境配置。 amd: 32位X86 amd64: 64位X86 arm: 32位ARM arm64: 64位ARM amd64是X86架构的CPU,64位版。amd64又叫X86_64。主流的桌面PC&am…...
Ansible 企业实战详解
一、ansible简介1. ansible是什么2.ansible的特点ansible的架构图 二、ansible 任务执行1、ansible 任务执行模式2、ansible 执行流程3、ansible 命令执行过程 二 .Ansible安装部署1.yum安装2.ansible 程序结构3、ansible配置文件查找顺序4、ansible配置文件5.ansible自动化配置…...

云贝教育 |【技术文章】pg缓存插件介绍
一、pg_buffercache 主要作用是查看pg的共享池中缓存的对象信息 1.1 创建扩展 postgres# create extension pg_buffercache; CREATE EXTENSION 1.2 查看视图pg_buffercache postgres# \d pg_buffercacheView "public.pg_buffercache"Column | Type | Co…...

Kohana框架的安装及部署
Kohana框架的安装及部署 tipsKohana安装以及部署1、重要文件作用说明1.1 /index.php1.2 /application/bootstrap.php 2、项目结构3、路由配置3.1、隐藏项目入口的路由3.2、配置默认路由3.3、配置自定义的路由(Controller目录下的控制器)3.4、配置自定义的路由(Controller/direc…...

无重复字符的最长子串 Golang leecode_3
刚开始的思路,先不管效率,跑出来再说,然后再进行优化。然后就有了下面的暴力代码: func lengthOfLongestSubstring(s string) int {// count 用来记录当前最长子串长度var count int// flag 用来对下面两个 if 语句分流var flag …...
Vue项目的学习一
1、Vue项目里面的.js文件里面对象添加属性 例如:在对象:row,需要在对象row里面添加一个属性状态:type,使用里面的Vue.set函数 Vue.set(参数1,参数2,参数3) Vue.set(row,type,false)解析: 参数1࿱…...

k8s备份
cpu 磁盘io 往主的写,同步给备 rootk8s-etcd02:~# cat /etc/systemd/system/etcd.service [Unit] DescriptionEtcd Server Afternetwork.target Afternetwork-online.target Wantsnetwork-online.target Documentationhttps://github.com/coreos[Service] Typen…...

python自己造轮子使用
项目结构 首先,需要按照下列格式组织你的 package project (项目名称,随意,与package无关)|----package (这个才是包名)|----…...

Elastic stack8.10.4搭建、启用安全认证,启用https,TLS,SSL 安全配置详解
ELK大家应该很了解了,废话不多说开始部署 kafka在其中作为消息队列解耦和让logstash高可用 kafka和zk 的安装可以参考这篇文章 深入理解Kafka3.6.0的核心概念,搭建与使用-CSDN博客 第一步、官网下载安装包 需要 elasticsearch-8.10.4 logstash-8.…...
解决npm报错Error: error:0308010C:digital envelope routines::unsupported
解决npm报错Error: error:0308010C:digital envelope routines::unsupported。 解决办法;终端执行以下命令(windows): set NODE_OPTIONS--openssl-legacy-provider然后再执行 npm命令成功:...

高防IP是什么?有什么优势?
一.高防IP的概念 高防IP是指高防机房所提供的IP段,一种付费增值服务,主要是针对网络中的DDoS攻击进行保护。用户可以通过配置高防IP,把域名解析到高防IP上,引流攻击流量,确保源站的稳定可靠。 二.高防IP的原理 高防I…...
框架学习笔记)
php费尔康框架phalcon(费尔康)框架学习笔记
phalcon(费尔康)框架学习笔记 以实例程序invo为例(invo程序放在网站根目录下的invo文件夹里,推荐php版本>5.4) 环境不支持伪静态网址时的配置 第一步: 在app\config\config.ini文件中的[application]节点内修改baseUri参数值为/invo/index.php/或…...
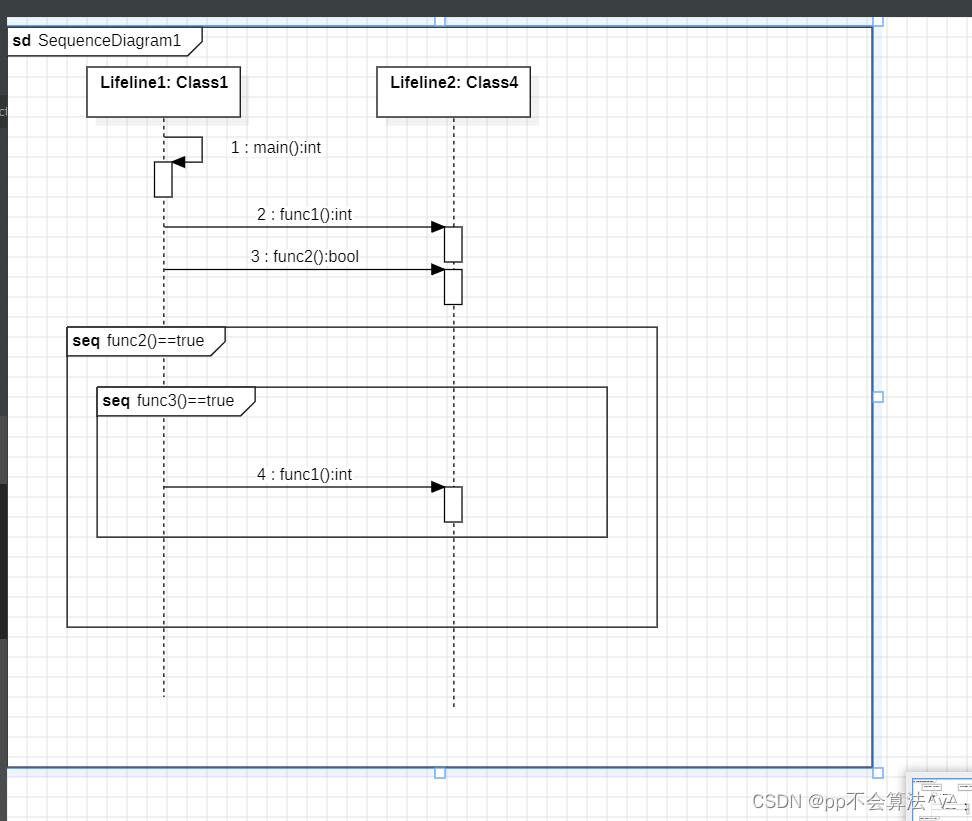
StartUML的基本使用
文章目录 简介和安装创建包创建类视图时序图 简介和安装 最近在学习一个项目的时候用到了StartUML来构造项目的类图和时序图 虽然vs2019有类视图,但是也不是很清晰,并没有生成uml图,但是宇宙最智能的IDE IDEA有生成uml图的功能 下面就简单介…...

飞天使-django概念之urls
urls 容易搞混的概念,域名,主机名,路由 网站模块多主机应用 不同模块解析不同的服务器ip地址 网页模块多路径应用 urlpatterns [ path(‘admin/’, admin.site.urls), path(‘’, app01views.index), path(‘movie/’, app01views.movi…...
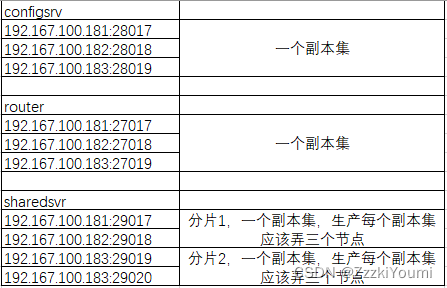
MongoDB分片集群搭建
----前言 mongodb分片 一般用得比较少,需要较多的服务器,还有三种的角色 一般把mongodb的副本集应用得好就足够用了,可搭建多套mongodb复本集 mongodb分片技术 mongodb副本集可以解决数据备份、读性能的问题,但由于mongodb副本集是…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
