《视觉SLAM十四讲》-- 后端 1(上)
文章目录
- 08 后端 1
- 8.1 概述
- 8.1.1 状态估计的概率解释
- 8.1.2 线性系统和卡尔曼滤波(KF)
- 8.1.3 非线性系统和扩展卡尔曼滤波(EKF)
- 8.1.4 小结
08 后端 1
前端视觉里程计可以给出一个短时间内的轨迹和地图,但由于不可避免的误差积累,地图在长时间内是不准确的,因此,我们希望构建一个大规模、长时间的最优轨迹和地图。
8.1 概述
8.1.1 状态估计的概率解释
(1)两种处理方式
-
批量式:使用过去和未来的信息来更新自己的状态的处理方式;
-
渐进式:仅适用过去的甚至仅是前一个时刻的信息来更新自己的状态的处理方式。
(2)运动方程和观测方程:
{ x k = f ( x k − 1 , u k ) + w k z k , j = h ( y j , x k ) + v k , j k = 1 , … , N , j = 1 , … , M (8-1) \left\{\begin{array}{l} \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k, j} \end{array} \quad k=1, \ldots, N, j=1, \ldots, M\right. \tag{8-1} {xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,jk=1,…,N,j=1,…,M(8-1)
以下图为例,只有运动方程时,由于误差的不断积累,位置的不确定性会不断增大;当加入正确的观测数据,不确定性就会减小,直至保持稳定。
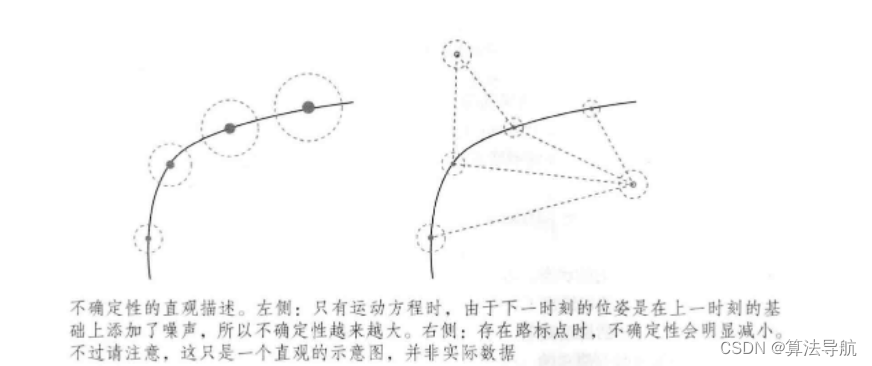
(3)将批量状态估计问题转化为最大似然估计问题,并使用最小二乘法求解。
定义 x k \boldsymbol{x}_k xk 为 k k k 时刻的所有变量,即包含此时刻的相机位姿和 m m m 个路标,
x k = def { x k , y 1 , … , y m } \boldsymbol{x}_{k} \stackrel{\text { def }}{=}\left\{\boldsymbol{x}_{k}, \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{m}\right\} xk= def {xk,y1,…,ym}
同时,把 k k k 时刻所有的观测记做 z k \boldsymbol{z}_k zk,于是式(8-1)可写为(注意区别)
{ x k = f ( x k − 1 , u k ) + w k z k = h ( x k ) + v k k = 1 , … , N (8-2) \left\{\begin{array}{l} \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=h\left( \boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k} \end{array} \quad k=1, \ldots, N\right. \tag{8-2} {xk=f(xk−1,uk)+wkzk=h(xk)+vkk=1,…,N(8-2)
我们希望用过去 0 到第 k k k 时刻所有的数据来估计现在的状态分布:
P ( x k ∣ x 0 , u 1 : k , z 1 : k ) P(\boldsymbol{x}_k|\boldsymbol{x}_0,\boldsymbol{u}_{1:k},\boldsymbol{z}_{1:k}) P(xk∣x0,u1:k,z1:k)
下标 1 : k 1:k 1:k 表示从 1 到 k k k 时刻所有的数据。
根据贝叶斯法则
P ( x k ∣ x 0 , u 1 : k , z 1 : k ) ∝ P ( z k ∣ x k ) P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) (8-3) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k}\right) \propto P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) \tag{8-3} P(xk∣x0,u1:k,z1:k)∝P(zk∣xk)P(xk∣x0,u1:k,z1:k−1)(8-3)
第一项称为 似然,第二项为 先验,将第二项以 x k − 1 \boldsymbol{x}_{k-1} xk−1 时刻为条件概率展开
P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1 (8-4) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=\int P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \tag{8-4} P(xk∣x0,u1:k,z1:k−1)=∫P(xk∣xk−1,x0,u1:k,z1:k−1)P(xk−1∣x0,u1:k,z1:k−1)dxk−1(8-4)
(可以这样理解,第一项表示 k k k 时刻状态和 k − 1 k-1 k−1 时刻有关,第二项表示 k − 1 k-1 k−1 时刻状态又与过去所有状态有关,这是一个递进的关系。)
在后续处理上,又有两种方式:一种是假设一阶马尔科夫性,即 k k k 时刻的状态只与 k − 1 k-1 k−1 时刻状态相关,这样就会得到以 扩展卡尔曼滤波 为代表的滤波器法;另一种是与之前所有的状态均相关,将得到 非线性优化 为主体的优化框架。目前,视觉 SLAM 的主流为非线性优化方法。
8.1.2 线性系统和卡尔曼滤波(KF)
(1)假设马尔可夫性,即当前时刻状态只与前一时刻的状态有关。则式(8-4)第一项可写为
P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k ∣ x k − 1 , u k ) (8-5) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) = P(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1},\boldsymbol{u}_k) \tag{8-5} P(xk∣xk−1,x0,u1:k,z1:k−1)=P(xk∣xk−1,uk)(8-5)
对于第二项,由于 k k k 时刻的输入量 u k \boldsymbol{u}_k uk 与 k − 1 k-1 k−1 时刻状态无关,则可将其化简为
P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k − 1 ∣ x 0 , u 1 : k − 1 , z 1 : k − 1 ) (8-6) P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k-1}, \boldsymbol{z}_{1: k-1}\right) \tag{8-6} P(xk−1∣x0,u1:k,z1:k−1)=P(xk−1∣x0,u1:k−1,z1:k−1)(8-6)
(2)首先推导 线性高斯系统 的卡尔曼滤波器(也就是说,运动方程和观测方程可以由线性方程来描述):
{ x k = A k x k − 1 + u k + w k z k = C k x k + v k k = 1 , … , N (8-8) \left\{\begin{array}{l} \boldsymbol{x}_{k}=\boldsymbol{A}_{k} \boldsymbol{x}_{k-1}+\boldsymbol{u}_{k}+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=\boldsymbol{C}_{k} \boldsymbol{x}_{k}+\boldsymbol{v}_{k} \end{array} \quad k=1, \ldots, N\right. \tag{8-8} {xk=Akxk−1+uk+wkzk=Ckxk+vkk=1,…,N(8-8)
假设噪声符合零均值高斯分布,即
w k ∼ N ( 0 , R ) . v k ∼ N ( 0 , Q ) (8-9) \boldsymbol{w}_{k} \sim N(\mathbf{0}, \boldsymbol{R}) . \quad \boldsymbol{v}_{k} \sim N(\mathbf{0}, \boldsymbol{Q}) \tag{8-9} wk∼N(0,R).vk∼N(0,Q)(8-9)
假设已知 k − 1 k-1 k−1 时刻的后验状态估计 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 及其协方差 P ^ k − 1 \hat{\boldsymbol{P}}_{k-1} P^k−1,现在根据 k k k 时刻的输入和观测数据,确定 x k \boldsymbol{x}_k xk 的后验分布。我们约定以上帽子 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 表示后验,下帽子 x ˇ k \check{\boldsymbol{x}}_{k} xˇk 表示先验分布。
根据 高斯分布线性组合性质,先通过运动方程确定 x k \boldsymbol{x}_k xk 的先验分布
P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) = N ( A k x ^ k − 1 + u k , A k P ^ k − 1 A k T + R ) (8-10) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=N(\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R}) \tag{8-10} P(xk∣x0,u1:k,z1:k−1)=N(Akx^k−1+uk,AkP^k−1AkT+R)(8-10)
这一步称为 预测 ,它显示了如何从上一时刻的状态,根据输入信息推断当前时刻的状态分布。这个分布就是 先验,记
x k ˇ = A k x ^ k − 1 + u k , P ˇ k = A k P ^ k − 1 A k T + R (8-11) \check{\boldsymbol{x}_k}=\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \quad \check{\boldsymbol{P}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R} \tag{8-11} xkˇ=Akx^k−1+uk,Pˇk=AkP^k−1AkT+R(8-11)
由观测方程,我们可以计算在某个状态下应该产生怎样的观测数据,
P ( z k ∣ x k ) = N ( C k x k , Q ) ) (8-12) P(\boldsymbol{z}_k|\boldsymbol{x}_k)=N(\boldsymbol{C}_{k} \boldsymbol{x}_{k},\boldsymbol{Q})) \tag{8-12} P(zk∣xk)=N(Ckxk,Q))(8-12)
为了得到 x k \boldsymbol{x}_k xk 的后验概率,我们需要计算它们的乘积,也就是式(8-3)。设最终的结果为 x k ∼ N ( x ^ k , P ^ k ) \boldsymbol{x}_k \sim N(\hat{\boldsymbol{x}}_k, \hat{\boldsymbol{P}}_k) xk∼N(x^k,P^k) ,则
N ( x ^ k , P ^ k ) = η N ( C k x k , Q ) ) ⋅ N ( x ˇ k , P ˇ k ) (8-13) N(\hat{\boldsymbol{x}}_k, \hat{\boldsymbol{P}}_k)=\eta N(\boldsymbol{C}_{k} \boldsymbol{x}_{k},\boldsymbol{Q})) \cdot N(\check{\boldsymbol{x}}_k, \check{\boldsymbol{P}}_k) \tag{8-13} N(x^k,P^k)=ηN(Ckxk,Q))⋅N(xˇk,Pˇk)(8-13)
我们知道高维高斯分布的概率密度函数为
p ( x ) = 1 ( 2 π ) N det ( Σ ) exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x)=\frac{1}{\sqrt{(2 \pi)^{N} \operatorname{det}(\boldsymbol{\Sigma})}} \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right) p(x)=(2π)Ndet(Σ)1exp(−21(x−μ)TΣ−1(x−μ))
因此,将指数部分展开
( x k − x ^ k ) T P ^ k − 1 ( x k − x ^ k ) = ( z k − C k x k ) T Q − 1 ( z k − C k x k ) + ( x k − x ˇ k ) T P ˇ k − 1 ( x k − x ˇ k ) (8-14) (\boldsymbol{x}_k-\hat{\boldsymbol{x}}_k)^\mathrm{T}\hat{\boldsymbol{P}}_k^{-1}(\boldsymbol{x}_k-\hat{\boldsymbol{x}}_k)=\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \boldsymbol{x}_{k}\right)^{\mathrm{T}} \boldsymbol{Q}^{-1}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \boldsymbol{x}_{k}\right)+\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right)^{\mathrm{T}} \check{\boldsymbol{P}}_{k}^{-1}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right) \tag{8-14} (xk−x^k)TP^k−1(xk−x^k)=(zk−Ckxk)TQ−1(zk−Ckxk)+(xk−xˇk)TPˇk−1(xk−xˇk)(8-14)
为了求左侧的 x ^ k \hat{\boldsymbol{x}}_k x^k 和 P ^ k \hat{\boldsymbol{P}}_k P^k ,将两侧展开,并比较一次和二次项系数。对于二次系数
P ^ k − 1 = C k T Q − 1 C k + P ˇ k − 1 (8-15) \hat{\boldsymbol{P}}_{k}^{-1}=\boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k}+\check{\boldsymbol{P}}_{k}^{-1} \tag{8-15} P^k−1=CkTQ−1Ck+Pˇk−1(8-15)
该式给出了协方差的计算过程。这里定义一个中间变量
K = P ^ k C k T Q − 1 (8-16) \boldsymbol{K}=\hat{\boldsymbol{P}}_{k}\boldsymbol{C}_{k}^{\mathrm{T}}\boldsymbol{Q}^{-1} \tag{8-16} K=P^kCkTQ−1(8-16)
将式(8-15)两侧时左乘乘 P ^ k \hat{\boldsymbol{P}}_{k} P^k,得
I = P ^ k C k T Q − 1 C k + P ^ k P ˇ k − 1 = K C k + P ^ k P ˇ k − 1 (8-17) \boldsymbol{I}=\hat{\boldsymbol{P}}_{k}\boldsymbol{C}_{k}^{\mathrm{T}}\boldsymbol{Q}^{-1}\boldsymbol{C}_{k}+\hat{\boldsymbol{P}}_{k}\check{\boldsymbol{P}}_{k}^{-1}=\boldsymbol{K}\boldsymbol{C}_{k}+\hat{\boldsymbol{P}}_{k}\check{\boldsymbol{P}}_{k}^{-1} \tag{8-17} I=P^kCkTQ−1Ck+P^kPˇk−1=KCk+P^kPˇk−1(8-17)
于是,得
P ^ k = ( I − K C k ) P ˇ k (8-18) \hat{\boldsymbol{P}}_{k}=(\boldsymbol{I}-\boldsymbol{K}\boldsymbol{C}_{k})\check{\boldsymbol{P}}_{k} \tag{8-18} P^k=(I−KCk)Pˇk(8-18)
然后比较一次项的系数
− 2 x ^ k T P ^ k − 1 x k = − 2 z k T Q − 1 C k x k − 2 x ˇ k T P ˇ k − 1 x k (8-19) -2 \hat{\boldsymbol{x}}_{k}^{\mathrm{T}} \hat{\boldsymbol{P}}_{k}^{-1} \boldsymbol{x}_{k}=-2 \boldsymbol{z}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k} \boldsymbol{x}_{k}-2 \check{\boldsymbol{x}}_{k}^{\mathrm{T}} \check{\boldsymbol{P}}_{k}^{-1} \boldsymbol{x}_{k} \tag{8-19} −2x^kTP^k−1xk=−2zkTQ−1Ckxk−2xˇkTPˇk−1xk(8-19)
整理,得
P ^ k − 1 x ^ k = C k T Q − 1 z k + P ˇ k − 1 x ˇ k (8-20) \hat{\boldsymbol{P}}_{k}^{-1} \hat{\boldsymbol{x}}_{k}=\boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{z}_{k}+\check{\boldsymbol{P}}_{k}^{-1} \check{\boldsymbol{x}}_{k} \tag{8-20} P^k−1x^k=CkTQ−1zk+Pˇk−1xˇk(8-20)
两侧同时左乘 P ^ k \hat{\boldsymbol{P}}_{k} P^k,并代入式(8-16)
x ^ k = P ^ k C k T Q − 1 z k + P ^ k P ˇ k − 1 x ˇ k = K z k + ( I − K C k ) x ˇ k = x ˇ k + K ( z k − C k x ˇ k ) (8-21) \begin{aligned} \hat{\boldsymbol{x}}_{k} &=\hat{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{z}_{k}+\hat{\boldsymbol{P}}_{k} \check{\boldsymbol{P}}_{k}^{-1} \check{\boldsymbol{x}}_{k} \\ &=\boldsymbol{K} \boldsymbol{z}_{k}+\left(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{C}_{k}\right) \check{\boldsymbol{x}}_{k}=\check{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \check{\boldsymbol{x}}_{k}\right) \end{aligned} \tag{8-21} x^k=P^kCkTQ−1zk+P^kPˇk−1xˇk=Kzk+(I−KCk)xˇk=xˇk+K(zk−Ckxˇk)(8-21)
至此,我们得到了后验协方差 P ^ k \hat{\boldsymbol{P}}_{k} P^k(式(8-15))和均值 x ^ k \hat{\boldsymbol{x}}_{k} x^k (式8-21)的表达式。
(3)线性卡尔曼滤波可归纳为 预测 和 更新 两个步骤:
——————————————————————————————————————————————————————————
① 预测:
x k ˇ = A k x ^ k − 1 + u k , P ˇ k = A k P ^ k − 1 A k T + R \check{\boldsymbol{x}_k}=\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \quad \check{\boldsymbol{P}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R} xkˇ=Akx^k−1+uk,Pˇk=AkP^k−1AkT+R
② 更新:先计算卡尔曼增益 K \boldsymbol{K} K(这与前面 定义的 K \boldsymbol{K} K 形式有所差别,但实际上是等价的 )
K = P ˇ k C k T ( C k P ˇ k C k T + Q k ) − 1 \boldsymbol{K}=\check{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}}\left(\boldsymbol{C}_{k} \check{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}}+\boldsymbol{Q}_{k}\right)^{-1} K=PˇkCkT(CkPˇkCkT+Qk)−1
再计算后验概率分布
x ^ k = x ˇ k + K ( z k − C k x ˇ k ) P ^ k = ( I − K C k ) P ˇ k \begin{aligned} \hat{\boldsymbol{x}}_{k}&=\check{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \check{\boldsymbol{x}}_{k}\right) \\ \hat{\boldsymbol{P}}_{k}&=(\boldsymbol{I}-\boldsymbol{K}\boldsymbol{C}_{k})\check{\boldsymbol{P}}_{k} \end{aligned} x^kP^k=xˇk+K(zk−Ckxˇk)=(I−KCk)Pˇk
——————————————————————————————————————————————————————————
这就是经典卡尔曼滤波中的五个公式。事实上,卡尔曼滤波还有其他的表达形式。
8.1.3 非线性系统和扩展卡尔曼滤波(EKF)
实际上,SLAM 中的运动方程和观测方程都是非线性的,而高斯分布经过非线性变换,其结果往往也不再是高斯分布。因此,在非线性系统中,必须取一定的近似,将非高斯分布近似为高斯分布。
(1)我们希望将上面的线性卡尔曼滤波器扩展到非线性系统中。即在某点附近,将运动方程和观测方程一阶泰勒展开,只保留一阶项(线性部分),然后按照线性系统进行推导。
假设 k − 1 k-1 k−1 时刻的均值和协方差矩阵为 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 和 P ^ k − 1 \hat{\boldsymbol{P}}_{k-1} P^k−1,在 k k k 时刻,把运动方程和观测方程在 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 、 P ^ k − 1 \hat{\boldsymbol{P}}_{k-1} P^k−1 处一阶展开,有
x k ≈ f ( x ^ k − 1 , u k ) + ∂ f ∂ x k − 1 ∣ x ^ k − 1 ( x k − 1 − x ^ k − 1 ) + w k (8-22) \boldsymbol{x}_{k} \approx f\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_{k}\right)+\left.\frac{\partial f}{\partial \boldsymbol{x}_{k-1}}\right|_{\hat{\boldsymbol{x}}_{k-1}}\left(\boldsymbol{x}_{k-1}-\hat{\boldsymbol{x}}_{k-1}\right)+\boldsymbol{w}_{k} \tag{8-22} xk≈f(x^k−1,uk)+∂xk−1∂f x^k−1(xk−1−x^k−1)+wk(8-22)
记
F = ∂ f ∂ x k − 1 ∣ x ^ k − 1 (8-23) \boldsymbol{F}=\left.\frac{\partial f}{\partial \boldsymbol{x}_{k-1}}\right|_{\hat{\boldsymbol{x}}_{k-1}} \tag{8-23} F=∂xk−1∂f x^k−1(8-23)
同样,对观测方程,在 x k \boldsymbol{x}_k xk 处展开
z k ≈ h ( x ˇ ) + ∂ h ∂ x k ∣ x ˇ k ( x k − x ˇ k ) + n k (8-24) \boldsymbol{z}_{k} \approx h\left(\check{\boldsymbol{x}}\right)+\left.\frac{\partial h}{\partial \boldsymbol{x}_{k}}\right|_{\check{\boldsymbol{x}}_{k}}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right)+\boldsymbol{n}_{k} \tag{8-24} zk≈h(xˇ)+∂xk∂h xˇk(xk−xˇk)+nk(8-24)
记
H = ∂ h ∂ x k ∣ x ˇ k (8-25) \boldsymbol{H}=\left.\frac{\partial h}{\partial \boldsymbol{x}_{k}}\right|_{\check{\boldsymbol{x}}_{k}} \tag{8-25} H=∂xk∂h xˇk(8-25)
类似式(8-10),根据运动方程得到 x k \boldsymbol{x}_k xk 的先验分布
P ( x k ∣ x 0 , u 1 : k , z 0 : k − 1 ) = N ( f ( x ^ k − 1 , u k ) , F P ^ k − 1 F T + R k ) (8-26) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{0: k-1}\right)=N(f\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_{k}\right), \boldsymbol{F} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{R}_k) \tag{8-26} P(xk∣x0,u1:k,z0:k−1)=N(f(x^k−1,uk),FP^k−1FT+Rk)(8-26)
记先验的均值和协方差为
x ˇ k = f ( x ^ k − 1 , u k ) , P ˇ k = F P ^ k − 1 F T + R k (8-27) \check{\boldsymbol{x}}_k=f(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_{k}), \quad \check{\boldsymbol{P}}_k=\boldsymbol{F} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{R}_k \tag{8-27} xˇk=f(x^k−1,uk),Pˇk=FP^k−1FT+Rk(8-27)
在观测中,有
P ( z k ∣ x k ) = N ( h ( x ˇ ) + H ( x k − x ˇ k ) , Q k ) (8-28) P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right)=N(h\left(\check{\boldsymbol{x}}\right)+\boldsymbol{H}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right), \boldsymbol{Q}_k) \tag{8-28} P(zk∣xk)=N(h(xˇ)+H(xk−xˇk),Qk)(8-28)
类似线性卡尔曼滤波,定义增益 K k \boldsymbol{K}_k Kk
K k = P k ˇ H T ( H P k ˇ H T + Q k ) ) − 1 (8-29) \boldsymbol{K}_k=\check{\boldsymbol{P}_k}\boldsymbol{H}^\mathrm{T}(\boldsymbol{H}\check{\boldsymbol{P}_k}\boldsymbol{H}^\mathrm{T}+\boldsymbol{Q}_k))^{-1} \tag{8-29} Kk=PkˇHT(HPkˇHT+Qk))−1(8-29)
那么, x k \boldsymbol{x}_k xk 的后验概率分布为
x ^ k = x ˇ k + K k ( z k − h ( x ˇ k ) ) , P ^ k = ( I − K k H ) P ˇ k (8-29) \hat{\boldsymbol{x}}_k=\check{\boldsymbol{x}}_k+\boldsymbol{K}_k(z_k-h(\check{\boldsymbol{x}}_k)), \quad \hat{\boldsymbol{P}}_k=(\boldsymbol{I}-\boldsymbol{K}_k\boldsymbol{H})\check{\boldsymbol{P}}_k \tag{8-29} x^k=xˇk+Kk(zk−h(xˇk)),P^k=(I−KkH)Pˇk(8-29)
8.1.4 小结
EKF 的优点:
-
推导简单,适用于各种形式传感器;
-
易做多传感器融合。
EKF 的缺点
-
一阶马尔科夫性过于简单;
-
可能会发散;
-
线性化误差;
-
从程序实现上来说,需要储存所有状态量的均值和方差,不适用于大型场景。
相关文章:

《视觉SLAM十四讲》-- 后端 1(上)
文章目录 08 后端 18.1 概述8.1.1 状态估计的概率解释8.1.2 线性系统和卡尔曼滤波(KF)8.1.3 非线性系统和扩展卡尔曼滤波(EKF)8.1.4 小结 08 后端 1 前端视觉里程计可以给出一个短时间内的轨迹和地图,但由于不可避免的…...

南昌市西湖区棒球特色规划
西湖区棒球特色学校打造方案 一、项目背景 南昌市西湖区作为江西省的教育强区,一直致力于发展特色教育。近年来,棒球运动逐渐受到广泛关注,西湖区决定将棒球运动作为特色项目,打造一所具有国际水平的棒球特色学校。 二、目标与…...
nginx启动命令
普通启动 切换到nginx安装目录的sbin目录下,执行:./nginx 通过配置文件启动 ./nginx -c /usr/local/nginx/conf/nginx.conf /usr/local/nginx/sbin/nginx -c /usr/local/nginx/conf/nginx.conf 其中-c是指定配置文件,而且配置文件路径必须指定绝对路…...

防爆五参数气象仪的科技力量
WX-FBQ2 随着科技的不断进步,气象监测设备也在不断升级和完善。 防爆五参数气象仪是一种可以同时监测温度、湿度、压力、风速和风向五个基本气象参数的仪器。它采用了气象监测技术,不仅可以实时监测气象数据,还可以对数据进行分析和处理。 …...
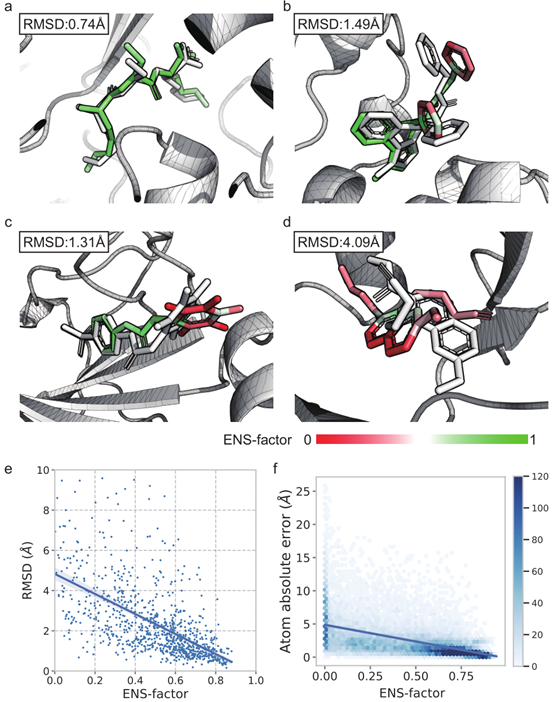
J. Chem. Theory Comput. | AI驱动的柔性蛋白-小分子复合物建模
今天为大家介绍的是来自陈语谦教授团队发表在Journal of Chemical Theory and Computation的论文,“Equivariant Flexible Modeling of the Protein−Ligand Binding Pose with Geometric Deep Learning”,博士生董铁君为第一作者。该文提出了一种新的AI…...
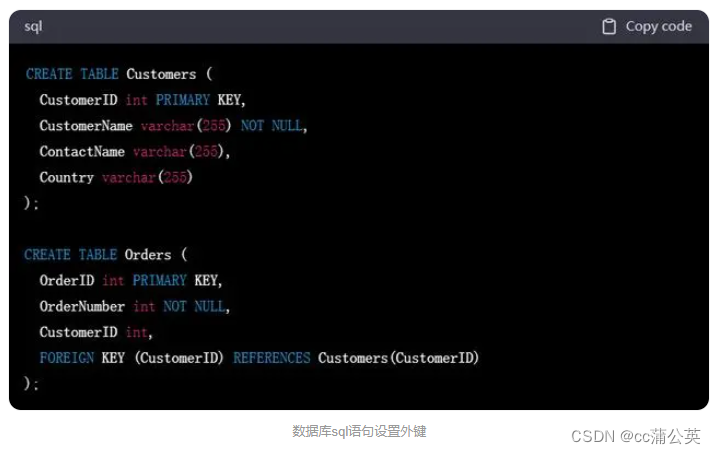
数据库sql语句设置外键
当我们需要在数据库表之间建立关联关系时,可以使用外键(Foreign Key)来实现。在 SQL 中,外键可以用来保持数据的完整性,并帮助我们更有效地管理数据。以下是设置外键的步骤: 1.在创建表时,需要…...
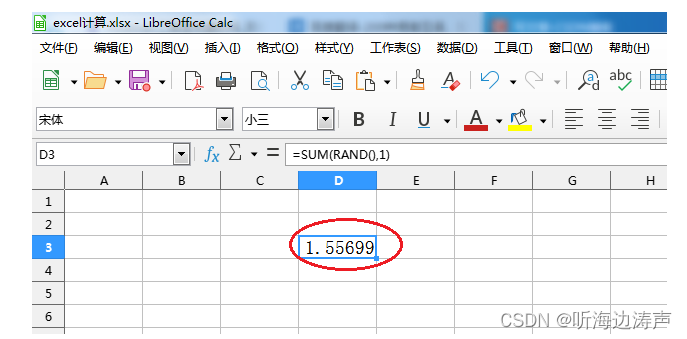
excel在函数中插入函数
例如,要计算RAND()1的值,其中RAND()表示取0~1之间的随机数。 插入-》函数: 选SUM函数: 点击“继续”: 将光标先放在数字1中的输入框中,然后在左边过滤出RAND函数,并且点击继续࿱…...

保姆级前端翻牌效果(CSS)
效果 翻牌效果 hover 时候 代码直接上 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document<…...

Mac环境配置的相关知识
Mac中配置环境的三个途径: 1.open/vim /etc/profile (建议不修改这个文件)全局(公有)配置,不管是哪个用户,登录时都会读取该文件(一般在这个文件中添加系统级环境变量) 2./etc/bashrc全局(公有)配置,bash shell执行时࿰…...

业务连续性:确保稳健运营的关键战略
在今天的快节奏商业环境中,保障业务连续性是企业成功的重要保障。业务连续性不仅仅是关于应对自然灾害或技术故障,更是一项战略,涉及组织的整体准备、规划和应对能力,以确保在各种情况下业务的稳健运营。 一、业务连续性的定义 业…...

【Pytorch和深度学习】栏目导读
一、栏目说明 本栏目《pytorch实践》是为初学者入门深度学习准备的。本文是该栏目的导读部分,因为计划本栏目在明年完成,因此,导读部分,即本文也在持续更新中。 本栏目设计目标是将深度学习全面用pytorch实践一遍,由浅…...

sklearn笔记:neighbors.NearestNeighbors
1 最近邻 class sklearn.neighbors.NearestNeighbors(*, n_neighbors5, radius1.0, algorithmauto, leaf_size30, metricminkowski, p2, metric_paramsNone, n_jobsNone)邻居搜索算法的选择通过关键字 algorithm 控制,它必须是 [auto, ball_tree, kd_tree, brute] …...

V-for中 key 值的作用,如何选择key
Vue.js 中的 v-for 指令是一个强大的工具,可以用于循环渲染列表数据。在使用 v-for 指令时,我们经常需要为每个循环项指定一个 key 值。本文将深入探讨 key 值的作用,并为您提供如何选择 key 值的建议和指导。 开始 在开始之前,让…...

linux内核驱动开发
系列文章目录 主要介绍linux系统下的驱动开发 文章目录 系列文章目录 文章目录 前言 一、驱动是什么? 二、主要分类 2.读入数据 3.代码示例 总结 前言 对设备驱动最通俗的解释就是“驱使硬件设备行动”。驱动与底层硬件直接打交道,按照硬件设备的具体工作方式,读写…...

2.3.5 交换机的VRRP技术
实验2.3.5 交换机的VRRP技术 一、任务描述二、任务分析三、具体要求四、实验拓扑五、任务实施1.交换机的基本配置 六、任务验收七、任务小结 一、任务描述 某公司的网络核心层原来采用一台三层交换机,随着网络应用的日益增多,对网络的可靠性也提出了越来…...
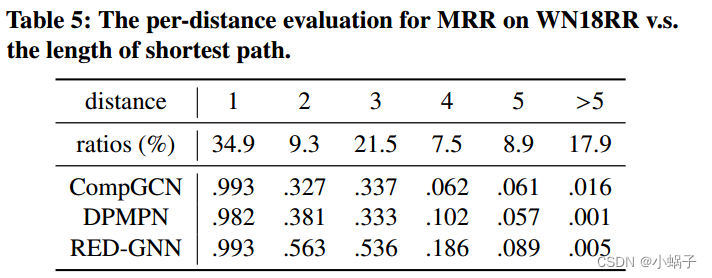
Knowledge Graph Reasoning with Relational Digraph
摘要: 知识图推理的目的是从已有的事实中推断出新的事实。基于关系路径的推理方法具有较强的可解释性和可转移性。然而,路径在捕获图中的局部证据方面自然受到限制。在本文中,我们引入了一种新的关系结构,即关系有向图(r-digraph)࿰…...
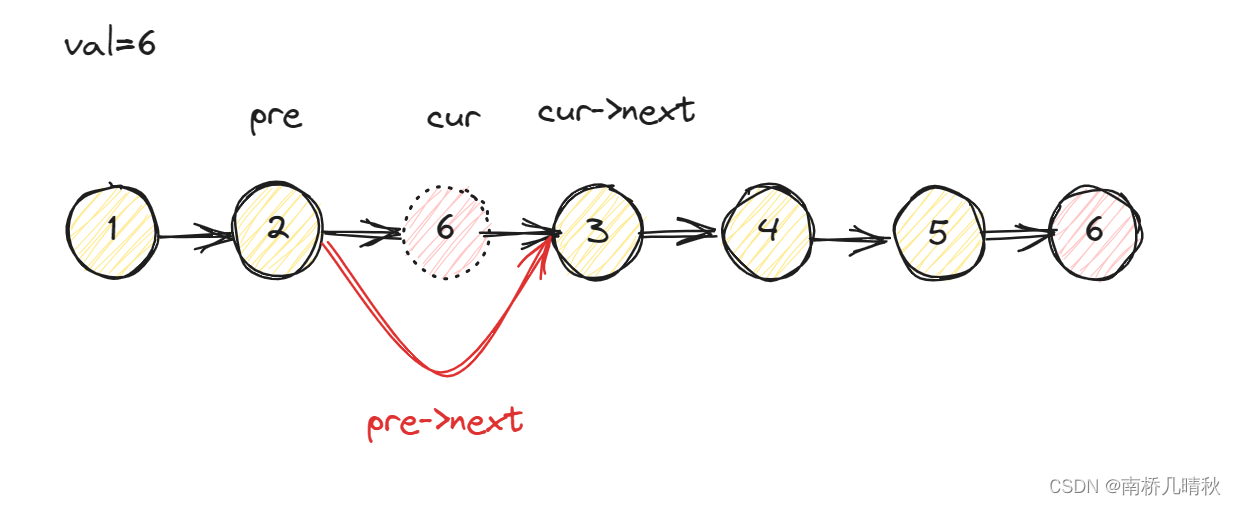
力扣203:移除链表元素
力扣203:移除链表元素 题目描述: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出&a…...

Moto edge s pro手机 WIFI和蓝牙连接不上 解决方法分享
2021年12月入手一台Moto Edge S Pro 12256版,看着性价比很高,越用越垃圾。屏幕显示没有vivo亮丽/APP图标很丑/屏幕上一点点水就失灵/拍照片边缘是模糊的/系统几乎不更新。 以上都可以忍受,但是: 用一年不到,蓝牙不能…...
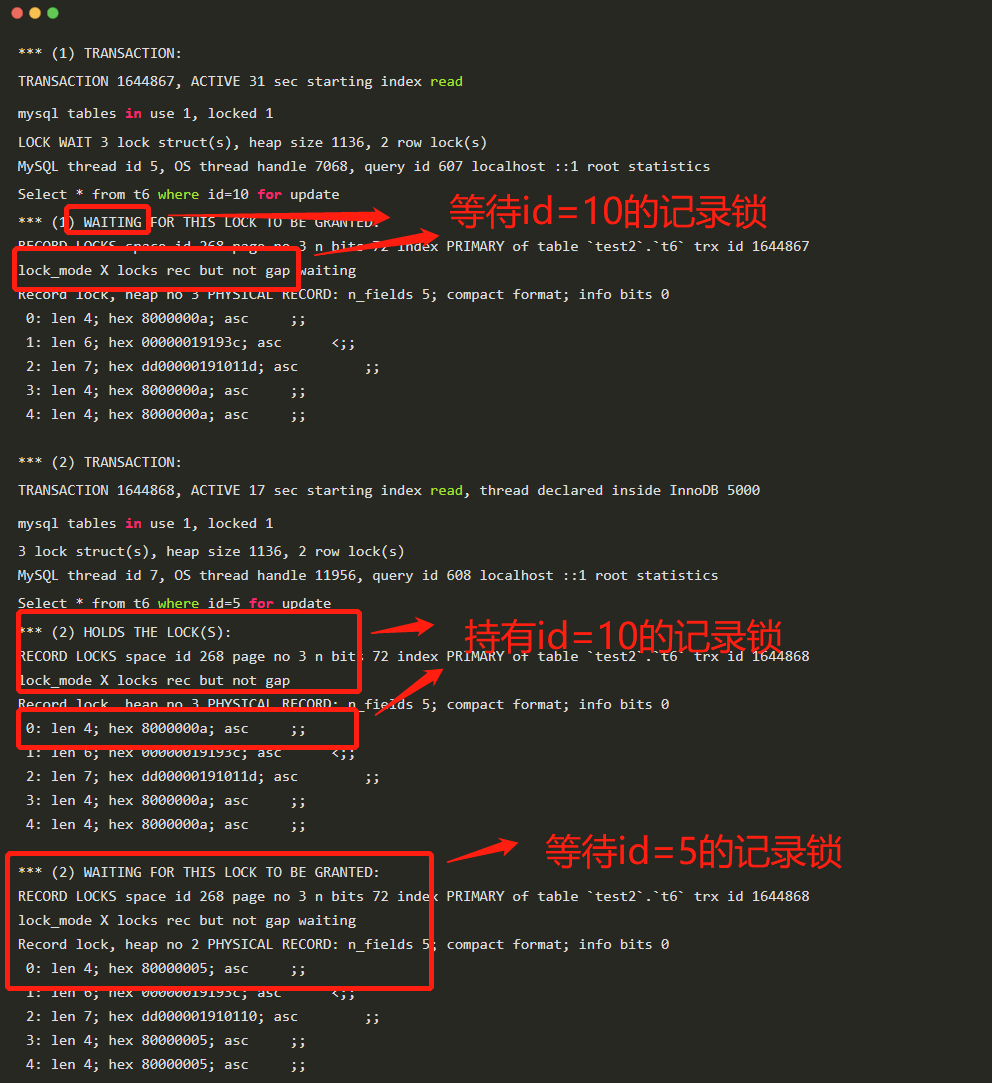
两万字图文详解!InnoDB锁专题!
前言 本文将跟大家聊聊 InnoDB 的锁。本文比较长,包括一条 SQL 是如何加锁的,一些加锁规则、如何分析和解决死锁问题等内容,建议耐心读完,肯定对大家有帮助的。 为什么需要加锁呢? InnoDB 的七种锁介绍 一条 SQL 是…...

2023湖南省赛
连接 目录 A:开开心心233 B:Square Game C:室温超导 F:necklace I:hard math J:radius K:tourist 补题中,会给出大部分代码 A:开开心心233 签到题 ,无论二分还是解方程还是直接for循环枚举都能直接通过啦 signed main() {ios_base:…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
