AK F.*ing leetcode 流浪计划之半平面求交
欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
本期话题:半平面求交
背景知识
学习资料
视频讲解
https://www.bilibili.com/video/BV1jL411C7Ct/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=fb27f95f25902a2cc94d4d8e49f5f777
文本资料
https://oi-wiki.org//geometry/half-plane/
基本问题转化
在很多题目中,给定的线段是没有方向的。此时,我们需要先把所有的线段都转化成点加向量的方式。使得向量的左边为有效区域。这样就可以使用模板求解了。
要注意的问题
- 主要的问题是浮点型的判断大小问题。在排序和判断点与线的关系时都用到浮点型判断。有些题型会卡精度,能用整数判断尽量不要使用浮点判断。
- atan2计算比较耗时,可以事先保存。
代码模板
求多边形的核
题目链接:https://vjudge.net/problem/UVA-1571
多边形的核就是取核区域内任意一点,站在该可以观察到多边形内任意一点。
利用半平面求交可以得到多边形的核
#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>
#include <list>
#include <cstring>
#include <set>using namespace std;
const double EPS = 1e-14;const int N = 2e6 + 10;int cmp(double d) {if (abs(d) < EPS)return 0;if (d > 0)return 1;return -1;
}class Point {
public:double x, y;int id;Point() {}Point(double a, double b) :x(a), y(b) {}Point(const Point& p) :x(p.x), y(p.y), id(p.id) {}void in() {scanf("%lf %lf", &x, &y);}void out() {printf("%.16f %.16f\n", x, y);}double dis() {return sqrt(x * x + y * y);}double dis2() {return x * x + y * y;}Point operator -() const {return Point(-x, -y);}Point operator -(const Point& p) const {return Point(x - p.x, y - p.y);}Point operator +(const Point& p) const {return Point(x + p.x, y + p.y);}Point operator *(double d)const {return Point(x * d, y * d);}Point operator /(double d)const {return Point(x / d, y / d);}void operator -=(Point& p) {x -= p.x;y -= p.y;}void operator +=(Point& p) {x += p.x;y += p.y;}void operator *=(double d) {x *= d;y *= d;}void operator /=(double d) {this ->operator*= (1 / d);}bool operator<(const Point& a) const {return x < a.x || (abs(x - a.x) < EPS && y < a.y);}bool operator==(const Point& a) const {return abs(x - a.x) < EPS && abs(y - a.y) < EPS;}
};// 向量操作double cross(const Point& a, const Point& b) {return a.x * b.y - a.y * b.x;
}double dot(const Point& a, const Point& b) {return a.x * b.x + a.y * b.y;
}class Line {
public:Point front, tail;double ang;int u, v;Line() {}Line(const Point& a, const Point& b) :front(a), tail(b) {ang = atan2(front.y - tail.y, front.x - tail.x);}
};int cmp(const Line& a, const Line& b) {//if (a.u == b.u && a.v == b.v)return 0;return cmp(a.ang - b.ang);}// 点在直线哪一边>0 左边,<0边
double SideJudge(const Line& a, const Point& b) {//return cmp(cross(a.front - a.tail, b - a.tail));return cross(a.front - a.tail, b - a.tail);
}int LineSort(const Line& a, const Line& b) {int c = cmp(a, b);if (c)return c < 0;return cross(b.front - b.tail, a.front - b.tail) > 0;
}/*
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
线段1 上1点用 p' = p+t*r (0<=t<=1)
线段2 上1点用 q' = q+u*s (0<=u<=1)
让两式相等求交点 p+t*r = q+u*s
两边都叉乘s
(p+t*r)Xs = (q+u*s)Xs
pXs + t*rXs = qXs
t = (q-p)Xs/(rXs)
同理,
u = (p-q)Xr/(sXr) -> u = (q-p)Xr/(rXs)以下分4种情况:
1. 共线,sXr==0 && (q-p)Xr==0, 计算 (q-p)在r上的投影在r长度上的占比t0,
计算(q+s-p)在r上的投影在r长度上的占比t1,查看[t0, t1]是否与范围[0,1]有交集。
如果t0>t1, 则比较[t1, t0]是否与范围[0,1]有交集。
t0 = (q-p)*r/(r*r)
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 平行sXr==0 && (q-p)Xr!=0
3. 0<=u<=1 && 0<=t<=1 有交点
4. 其他u, t不在0到范围内,没有交点。
*/
pair<double, double> intersection(const Point& q, const Point& s, const Point& p, const Point& r, bool &oneline) {// 计算 (q-p)Xrauto qpr = cross(q - p, r);auto qps = cross(q - p, s);auto rXs = cross(r, s);if (cmp(rXs) == 0) {oneline = true;return { -1, -1 }; // 平行或共线}// 求解t, u// t = (q-p)Xs/(rXs)auto t = qps / rXs;// u = (q-p)Xr/(rXs)auto u = qpr / rXs;return { u, t };
}Point LineCross(const Line& a, const Line& b, bool &f) {Point dira = a.front - a.tail;Point dirb = b.front - b.tail;bool oneline=false;auto p = intersection(a.tail, dira, b.tail, dirb, oneline);if (oneline)f = false;return a.tail + dira * p.first;
}class HalfPlane {
public:vector<Line> lines;vector<int> q;vector<Point> t;int len;HalfPlane() {lines.resize(N);q.resize(N);t.resize(N);}void reset() {len = 0;}void addLine(const Line& a) {lines[len++] = a;}bool run() {sort(lines.begin(), lines.begin() + len, LineSort);int l = -1, r = 0;q[0] = 0;for (int i = 1; i < len; ++i) {if (cmp(lines[i], lines[i - 1]) == 0)continue;while (r - l > 1 && SideJudge(lines[i], t[r]) < 0)r--;while (r - l > 1 && SideJudge(lines[i], t[l + 2]) < 0)l++;q[++r] = i;bool f=true;t[r] = LineCross(lines[q[r]], lines[q[r - 1]], f);}while (r - l > 1 && SideJudge(lines[q[l + 1]], t[r]) < 0)r--;//if (r - l > 1) {// bool f = true;// t[r + 1] = LineCross(lines[q[l + 1]], lines[q[r]], f);// r++;// if (!f)r -= 2;//} 统计交点//l++;//vector<Point> ans(r - l);//for (int i = 0; i < ans.size(); ++i) {// ans[i] = t[i + l + 1];//}return r-l>2;}
};Point oiPs[N * 2];
pair<int, int> ori[N * 2];
HalfPlane hp;int bigDevid(int a, int b) {for (int i = max(abs(a), abs(b)); i >= 1; i--) {if (a % i == 0 && b % i == 0)return i;}return 1;
}void solve() {int n, m = 1;//FILE* fp = fopen("ans.txt", "w");while (scanf("%d", &n) != EOF && n) {int a, b;for (int i = 0; i < n; ++i) {scanf("%d %d", &a, &b);oiPs[i] = Point(a, b);ori[i] = { a,b };}oiPs[n] = oiPs[0];ori[n] = ori[0];hp.reset();for (int i = 0; i < n; ++i) {hp.addLine(Line(oiPs[i+1], oiPs[i]));hp.lines[i].u = ori[i+1].first - ori[i].first;hp.lines[i].v = ori[i+1].second - ori[i].second;int bd = bigDevid(hp.lines[i].u, hp.lines[i].v);hp.lines[i].u /= bd;hp.lines[i].v /= bd;}auto ps = hp.run();if (ps)puts("1");else puts("0");m++;}
}int main() {solve();return 0;}/*
4
0 0
0 1
1 1
1 0
8
0 0
3 0
4 3
2 2
3 4
4 4
4 5
0 5
08
0 0
0 1
1 1
1 2
0 2
0 3
3 3
3 0
*/
练习一
链接:https://www.luogu.com.cn/problem/P4196
求多个凸多边形的交面积。
对每条边进行半平面求交,再利用三角形求多边形面积。
#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>
#include <list>
#include <cstring>
#include <set>using namespace std;
const double EPS = 1e-14;const int N = 2e6 + 10;int cmp(double d) {if (abs(d) < EPS)return 0;if (d > 0)return 1;return -1;
}class Point {
public:double x, y;int id;Point() {}Point(double a, double b) :x(a), y(b) {}Point(const Point& p) :x(p.x), y(p.y), id(p.id) {}void in() {scanf("%lf %lf", &x, &y);}void out() {printf("%.16f %.16f\n", x, y);}double dis() {return sqrt(x * x + y * y);}double dis2() {return x * x + y * y;}Point operator -() const {return Point(-x, -y);}Point operator -(const Point& p) const {return Point(x - p.x, y - p.y);}Point operator +(const Point& p) const {return Point(x + p.x, y + p.y);}Point operator *(double d)const {return Point(x * d, y * d);}Point operator /(double d)const {return Point(x / d, y / d);}void operator -=(Point& p) {x -= p.x;y -= p.y;}void operator +=(Point& p) {x += p.x;y += p.y;}void operator *=(double d) {x *= d;y *= d;}void operator /=(double d) {this ->operator*= (1 / d);}bool operator<(const Point& a) const {return x < a.x || (abs(x - a.x) < EPS && y < a.y);}bool operator==(const Point& a) const {return abs(x - a.x) < EPS && abs(y - a.y) < EPS;}
};// 向量操作double cross(const Point& a, const Point& b) {return a.x * b.y - a.y * b.x;
}double dot(const Point& a, const Point& b) {return a.x * b.x + a.y * b.y;
}class Line {
public:Point front, tail;double ang;int u, v;Line() {}Line(const Point& a, const Point& b) :front(a), tail(b) {ang = atan2(front.y - tail.y, front.x - tail.x);}
};int cmp(const Line& a, const Line& b) {//if (a.u == b.u && a.v == b.v)return 0;return cmp(a.ang - b.ang);}// 点在直线哪一边>0 左边,<0边
double SideJudge(const Line& a, const Point& b) {//return cmp(cross(a.front - a.tail, b - a.tail));return cross(a.front - a.tail, b - a.tail);
}int LineSort(const Line& a, const Line& b) {int c = cmp(a, b);if (c)return c < 0;return cross(b.front - b.tail, a.front - b.tail) > 0;
}/*
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
线段1 上1点用 p' = p+t*r (0<=t<=1)
线段2 上1点用 q' = q+u*s (0<=u<=1)
让两式相等求交点 p+t*r = q+u*s
两边都叉乘s
(p+t*r)Xs = (q+u*s)Xs
pXs + t*rXs = qXs
t = (q-p)Xs/(rXs)
同理,
u = (p-q)Xr/(sXr) -> u = (q-p)Xr/(rXs)以下分4种情况:
1. 共线,sXr==0 && (q-p)Xr==0, 计算 (q-p)在r上的投影在r长度上的占比t0,
计算(q+s-p)在r上的投影在r长度上的占比t1,查看[t0, t1]是否与范围[0,1]有交集。
如果t0>t1, 则比较[t1, t0]是否与范围[0,1]有交集。
t0 = (q-p)*r/(r*r)
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 平行sXr==0 && (q-p)Xr!=0
3. 0<=u<=1 && 0<=t<=1 有交点
4. 其他u, t不在0到范围内,没有交点。
*/
pair<double, double> intersection(const Point& q, const Point& s, const Point& p, const Point& r, bool &oneline) {// 计算 (q-p)Xrauto qpr = cross(q - p, r);auto qps = cross(q - p, s);auto rXs = cross(r, s);if (cmp(rXs) == 0) {oneline = true;return { -1, -1 }; // 平行或共线}// 求解t, u// t = (q-p)Xs/(rXs)auto t = qps / rXs;// u = (q-p)Xr/(rXs)auto u = qpr / rXs;return { u, t };
}Point LineCross(const Line& a, const Line& b, bool &f) {Point dira = a.front - a.tail;Point dirb = b.front - b.tail;bool oneline=false;auto p = intersection(a.tail, dira, b.tail, dirb, oneline);if (oneline)f = false;return a.tail + dira * p.first;
}class HalfPlane {
public:vector<Line> lines;void addLine(const Line& a) {lines.push_back(a);}vector<Point> run() {sort(lines.begin(), lines.end(), LineSort);vector<int> q(lines.size() + 10);vector<Point> t(lines.size() + 10);int l = -1, r = 0;q[0] = 0;for (int i = 1; i < lines.size(); ++i) {if (cmp(lines[i], lines[i - 1]) == 0)continue;while (r - l > 1 && SideJudge(lines[i], t[r]) < 0)r--;while (r - l > 1 && SideJudge(lines[i], t[l + 2]) < 0)l++;q[++r] = i;bool f = true;t[r] = LineCross(lines[q[r]], lines[q[r - 1]], f);}while (r - l > 1 && SideJudge(lines[q[l + 1]], t[r]) < 0)r--;if (r - l > 1) {bool f = true;t[r + 1] = LineCross(lines[q[l + 1]], lines[q[r]], f);r++;}// 统计交点l++;vector<Point> ans(r - l);for (int i = 0; i < ans.size(); ++i) {ans[i] = t[i + l + 1];}return ans;}
};Point oiPs[N];void solve() {int n, m;scanf("%d", &n);HalfPlane hp;int a, b;while (n--) {scanf("%d", &m);for (int i = 0; i < m; ++i) {scanf("%d%d", &a, &b);oiPs[i].x = a;oiPs[i].y = b;}oiPs[m] = oiPs[0];for (int i = 0; i < m; ++i) {hp.addLine(Line(oiPs[i + 1], oiPs[i]));}}auto keyPoints = hp.run();double ans = 0;for (int i = 2; i < keyPoints.size(); ++i) {ans += cross(keyPoints[i - 1] - keyPoints[0], keyPoints[i] - keyPoints[0]);}printf("%.3f\n", ans / 2);
}int main() {solve();return 0;}/*
3
3
-1 2
-2 1
-1 13
1 1
2 1
1 23
1 1
3 0
2 2*/
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。创作不易,帮忙点击公众号的链接。

相关文章:

AK F.*ing leetcode 流浪计划之半平面求交
欢迎关注更多精彩 关注我,学习常用算法与数据结构,一题多解,降维打击。 本期话题:半平面求交 背景知识 学习资料 视频讲解 https://www.bilibili.com/video/BV1jL411C7Ct/?spm_id_from333.1007.top_right_bar_window_history…...

docker搭建zokeeper集群、kafka集群
三台机器,ip分别为ip1,ip2,ip3 一、安装docker集群 1、三台机器分别拉取镜像 docker pull wurstmeister/zookeeper 2、三台机器分别运行容器 (1)第一台 docker run -d --restartalways --log-driver json-file --log-opt max-size100m --lo…...
【java学习—十四】反射机制调用指定方法、指定属性(5)
文章目录 1. 调用指定方法2. 调用指定属性 1. 调用指定方法 通过反射,调用类中的方法,通过 Method 类完成。步骤: ①通过 Class 类的 getMethod(String name,Class...parameterTypes) 方法取得一个 Method 对象,并设置此…...

PC端微信@所有人逻辑漏洞
(一)过程 这个漏洞是PC端微信,可以越权让非管理员艾特所有人,具体步骤如下 第一步:找一个自己的群(要有艾特所有人的权限)“123”是我随便输入的内容,可以更改,然后按c…...
如何在Windows 10中进行屏幕截图
本文介绍如何在Windows 10中捕获屏幕截图,包括使用键盘组合、使用Snipping Tool、Snipp&Sketch Tool或Windows游戏栏。 使用打印屏幕在Windows 10中捕获屏幕截图 在Windows 10中捕获屏幕截图的最简单方法是按下键盘上的PrtScWindows键盘组合。你将看到屏幕短暂…...
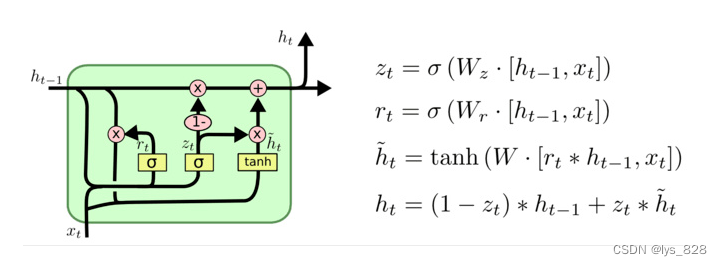
【nlp】2.4 GRU模型
GRU模型 1 GRU介绍2 GRU的内部结构图2.1 GRU结构分析2.2 Bi-GRU介绍2.3 使用Pytorch构建GRU模型2.4 GRU优缺点3 RNN及其变体1 GRU介绍 GRU(Gated Recurrent Unit)也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆…...

国科云:浅谈DNS缓存投毒常见类型和防御策略
为了提升解析效率减轻各级服务器的解析压力,DNS系统中引入了缓存机制,但这同样也带来了较大的安全隐患,为攻击者利用DNS缓存进行投毒攻击创造了条件,对DNS系统的安全造成了巨大破坏。本文国科云将分析缓存投毒的两种主要类型&…...
之tcpdump)
Linux命令(120)之tcpdump
linux命令之tcpdump 1.tcpdump介绍 linux命令tcpdump是用来将网络中传送的数据包完全截获下来以进行相关分析,常用的分析工具是wireshark 2.tcpdump用法 tcpdump [参数] tcpdump参数 参数说明-i指定端口-n指定协议-t在输出的每一行不打印时间戳-s抓取数据包时&a…...

2311rust对接C
原文 为了与其他语言通信,Rust提供了(FFI)外部函数接口.FFI是Rust和C间的函数调用,与C函数调用有相同性能的零成本抽象. FFI绑定还可利用(如所有权和借用)语言功能来提供强制指针和其他资源协议的安全接口. Rust与C对话 从Rust调用C代码的简单示例开始.如下为C代码: int do…...
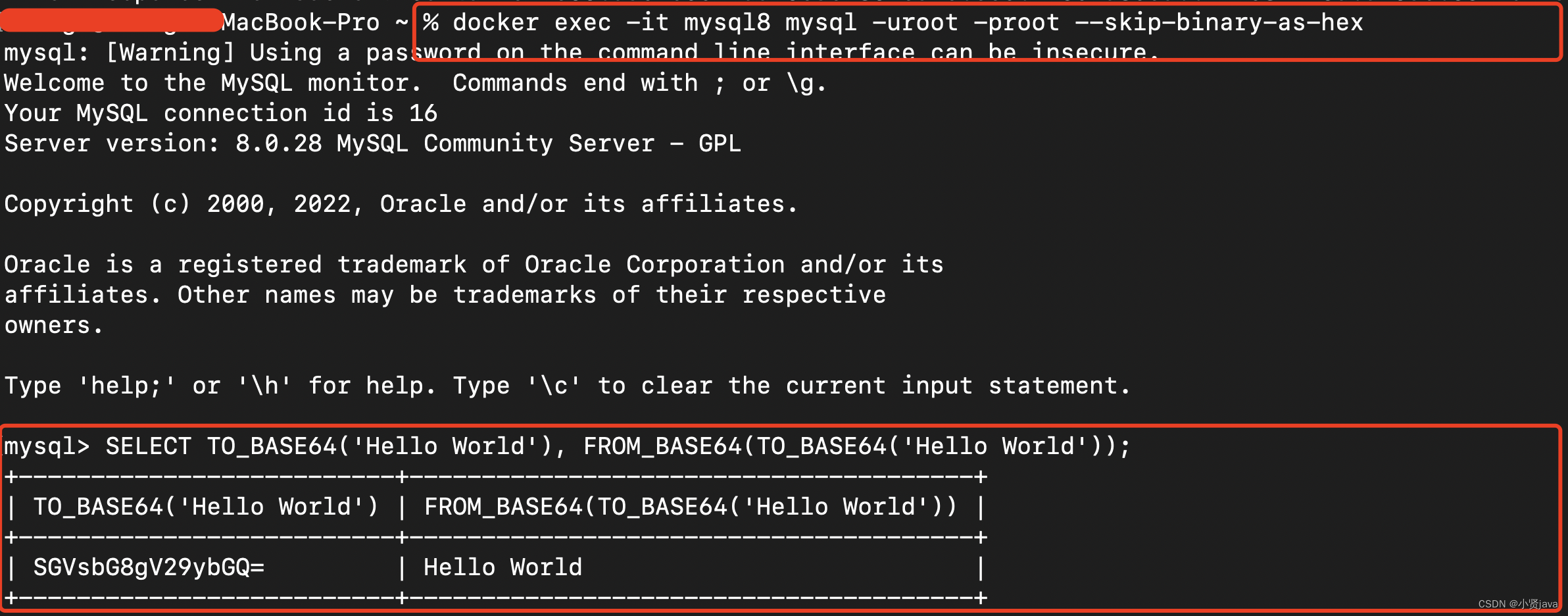
MYSQL字符串函数详解和实战(字符串函数大全,内含示例)
MySQL提供了许多字符串函数,用于处理和操作字符串数据。以下是一些常用的MYSQL字符串函数。 建议收藏以备后续用到查阅参考。 目录 一、CONCAT 拼接字符串 二、CONCAT_WS 拼接字符串 三、SUBSTR 取子字符串 四、SUBSTRING 取子字符串 五、SUBSTRING_INDEX 取子…...

从C语言到C++_40(多线程相关)C++线程接口+线程安全问题加锁(shared_ptr+STL+单例)
目录 1. C多线程 1.1 thread库 1.2 mutex库 1.3 RAII锁 1.4 atomicCAS 1.5 condition_variable 1.6 分别打印奇数和偶数 2. shared_ptr线程安全 2.1 库里面的shared_ptr使用 2.2 shared_ptr加锁代码 3. 单例模式线程安全 3.1 懒汉模式线程安全问题 3.2 懒汉模式最…...
)
Angular 指令介绍及使用(三)
Angular 指令概述 在 Angular 中,指令是一种机制,用于扩展和修改组件的行为和外观。指令可以由开发者自定义,也可以是 Angular 框架自带的一些内置指令。通过使用指令,我们可以在 HTML 模板中通过属性或元素名来操作组件。 Angu…...
小学生加减乘除闯关运算练习流量主微信小程序开发
小学生加减乘除闯关运算练习流量主微信小程序开发 经过本次更新,我们增加了新的功能和特性,以提升用户体验和运算练习的趣味性: 能量石与激励视频:用户可以通过观看激励视频来获取能量石,这些能量石可以用于解锁收费…...

普通测径仪升级的智能测径仪 增添11大实用功能!
普通测径仪能对各种钢材进行非接触式的外径及椭圆度在线检测,测量数据准确且无损,可测、监测、超差提示、系统分析等。在此基础上,为测径仪进行了进一步升级制成智能测径仪,为其增添更多智能化模块,让其使用更加方便。…...

vue做的一个一点就转的转盘(音乐磁盘),点击停止时会在几秒内缓慢停止,再次点击按钮可以再次旋转,
先看效果: 代码:主要部分我会红线画出来 css:部分: 源码: vue部分: <template><div class"song-lyric"><div><div class"type"><div class"right">&l…...
Spring6(一):入门案例
文章目录 1. 概述1.1 Spring简介1.2 Spring 的狭义和广义1.3 Spring Framework特点1.4 Spring模块组成 2 入门2.1 构建模块2.2 程序开发2.2.1 引入依赖2.2.2 创建java类2.2.3 创建配置文件2.2.4 创建测试类测试 2.3 程序分析2.4 启用Log4j2日志框架2.4.1 引入Log4j2依赖2.4.2 加…...

Linux中报错no space device解决思路
1,df -h :查看所有文件下的磁盘使用情况。注意,查询的最后一栏属性就是分区所在的目录路径 2,进到具体的文件下,接着命令:du -sh * | grep G 搜索G以上的文本。 没搜到内容的话,使用命令du -sh…...

vue3使用element-plus
安装 # NPM $ npm install element-plus --save# Yarn $ yarn add element-plus# pnpm $ pnpm install element-plus 全局引入 main.js // main.ts import { createApp } from vue import ElementPlus from element-plus//引入ElementPlus所有组件 import element-plus/dis…...

高质量实时渲染笔记
文章目录 Real-time shadows1 自遮挡问题2 解决阴影detach问题?3 Aliasing4 近似积分5 percentage closer soft shadows(PCSS)percenta closer filtering(PCF)PCSS的思想 6 Variance Soft Shadow Mapping (VSSM)步骤Moment Shadow Mapping 7 Distance field shadow …...
云原生下GIS服务规划与设计
作者:lisong 目录 背景云原生环境下GIS服务的相关概念GIS服务在云原生环境下的规划调度策略GIS服务在云原生环境下的调度手段GIS服务在云原生环境下的服务规划调度实践 背景 作为云原生GIS系统管理人员,在面对新建的云GIS系统时,通常需要应对…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
