【算法练习Day48】回文子串最长回文子序列

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 回文子串
- 最长回文子序列
- 总结:
回文子串
647. 回文子串 - 力扣(LeetCode)
给一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
- 确定dp数组(dp table)以及下标的含义
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
所以我们要看回文串的性质。
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 确定递推公式
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
-
dp数组如何初始化
dp[i][j]初始化为false。 -
确定遍历顺序
遍历顺序可有有点讲究了。
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角
如果矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
有的代码实现是优先遍历列,然后遍历行,其实也是一个道理,都是为了保证dp[i + 1][j - 1]都是经过计算的。
- 举例推导dp数组
举例,输入:“aaa”,dp[i][j]状态如下:
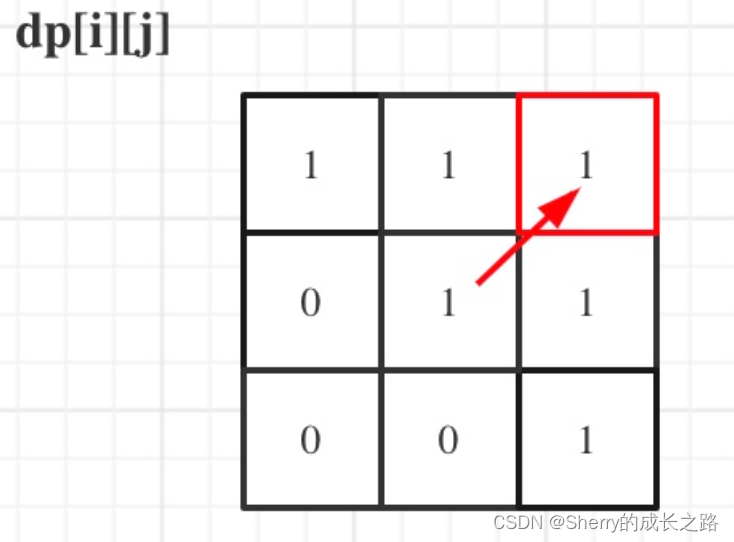
图中有6个true,所以就是有6个回文子串。
class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];for (boolean[] a: dp) {Arrays.fill(a,false);}int result = 0;for (int i = s.length()-1; i>=0 ; i--) {for (int j = i; j <s.length() ; j++) {if (s.charAt(i)==(s.charAt(j))) {if (j-i<=1){dp[i][j] = true;result++;}else if(dp[i+1][j-1]==true){dp[i][j] = true;result++;}}}}return result;}
}
最长回文子序列
516. 最长回文子序列 - 力扣(LeetCode)
给一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
动规五部曲分析如下:
-
确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。 -
确定递推公式
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如图:
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
- dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行,这样递推公式:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
- 确定遍历顺序
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j]和 dp[i][j - 1]
所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
j的话,可以正常从左向右遍历。
- 举例推导dp数组
输入s:“cbbd” 为例,dp数组状态如图:

红色框即:dp[0][s.size() - 1]; 为最终结果。
class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];for (int i = 0; i <s.length(); i++) {dp[i][i] = 1;}for (int i = s.length()-1; i >=0 ; i--) {for (int j =i+1; j <s.length(); j++) {if (s.charAt(i)==s.charAt(j)) dp[i][j]=dp[i+1][j-1]+2;else dp[i][j]=Math.max(dp[i][j-1],dp[i+1][j]);}}return dp[0][s.length()-1];}
}
总结:
今天我们完成了回文子串、最长回文子序列两道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【算法练习Day48】回文子串最长回文子序列
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 回文子串最长回文子序列总结…...
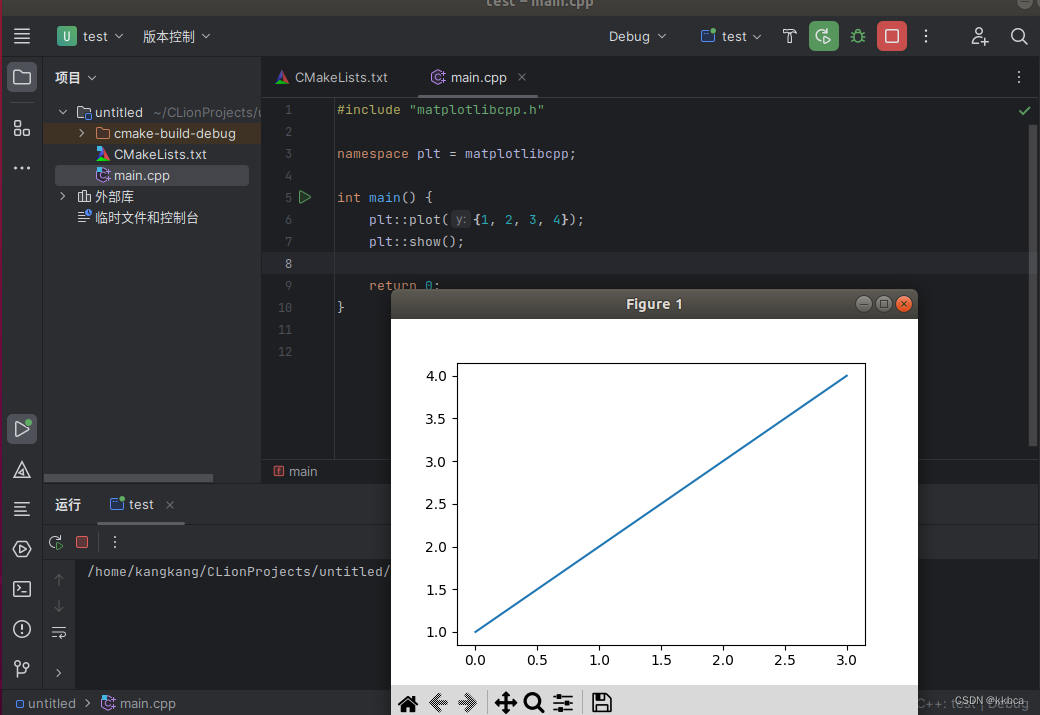
ubuntu下C++调用matplotlibcpp进行画图(超详细)
目录 一、换源 二、安装必要的软件 三、下载matplotlibcpp 四、下载anaconda 1.anaconda下载 2.使用anaconda配置环境 五、下载CLion 1.下载解压CLion 2.替换jbr文件夹 3.安装CLion 4.激活CLion 5.CLion汉化 6.Clion配置 六、使用CLion运行 七、总结 我的环…...

芯科科技推出新的8位MCU系列产品,扩展其强大的MCU平台
新的BB5系列为简单应用提供更多开发选择 中国,北京 - 2023年11月14日 – 致力于以安全、智能无线连接技术,建立更互联世界的全球领导厂商Silicon Labs(亦称“芯科科技”,NASDAQ:SLAB),今日宣布…...

Flink CDC
1、Flink CDC的介绍: 是一种技术,可以帮助我们实时的捕获数据库中数据的变化,并将这些变化的数据以流的形式传输到其他的系统中进行处理和存储。 2、Flink CDC的搭建: 1、开启mysql的binlog功能: # 1、修改mysql配置…...

数据结构-链表的简单操作代码实现3-LinkedList【Java版】
写在前: 本篇博客主要介绍关于双向链表的一些简答操作实现,其中有有部分代码的实现和前两篇博客中的单向链表是相类似的。例如:查找链表中是否包含关键字key、求链表的长度等。 其余的涉及到prev指向的需要特别注意,区分和单向链表之间的差异…...

JTS: 24 MinimumDiameter 最小矩形
文章目录 版本代码 版本 org.locationtech.jts:jts-core:1.19.0 链接: github 代码 package pers.stu.algorithm;import org.locationtech.jts.algorithm.MinimumDiameter; import org.locationtech.jts.geom.Coordinate; import org.locationtech.jts.geom.Geometry; import…...
MacOS Ventura 13 优化配置(ARM架构新手向导)
一、系统配置 1、About My MacBook Pro 2、在当前标签打开新窗口 桌面上创建目录的文件夹,每次新打开一个目录,就会创建一个窗口,这就造成窗口太多,不太好查看和管理,我们可以改成在新标签处打开新目录。需要在&…...
多区域OSPF配置
配置命令步骤: 1.使用router ospf 进程ID编号 启用OSPF路由 2.使用network 直连网络地址 反掩码 area 区域号 将其归于对应区域 注意: 1.进程ID编号可任意(1-65535) 2.反掩码用4个255相减得到 3.area 0 为主干区域 4.连接不…...

【强化学习】day1 强化学习基础、马尔可夫决策过程、表格型方法
写在最前:参加DataWhale十一月组队学习记录 【教程地址】 https://github.com/datawhalechina/joyrl-book https://datawhalechina.github.io/easy-rl/ https://linklearner.com/learn/detail/91 强化学习 强化学习是一种重要的机器学习方法,它使得智能…...

openwrt Docker不能联网
文章参考:docker上网(docker安装openwrt无法上网) - 老白网络 外网不能访问内网是应为防火墙。内网访问外网如下: 清理容器垃圾 docker volume prune -f 创建一个网络 docker network create --subnet172.18.0.0/16 mynet 通过该网络创建gerrit docker run -tid --name ge…...
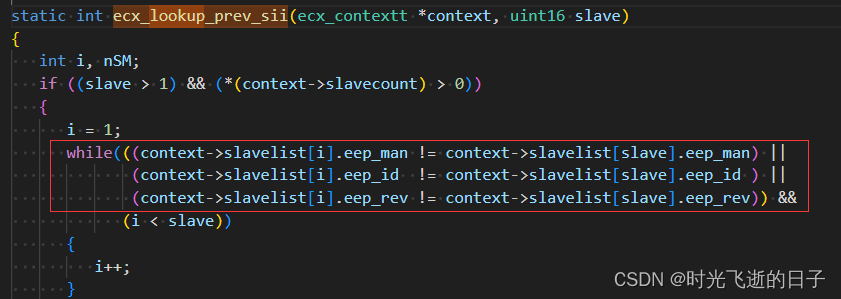
EtherCAT从站EEPROM组成信息详解(2):字8-15产品标识区
0 工具准备 1.EtherCAT从站EEPROM数据(本文使用DE3E-556步进电机驱动器)1 字8-字15产品标识区 1.1 产品标识区组成规范 对于不同厂家和型号的从站,主站是如何区分它们的呢?这就要提起SII的字8-字15区域存储的产品标识ÿ…...
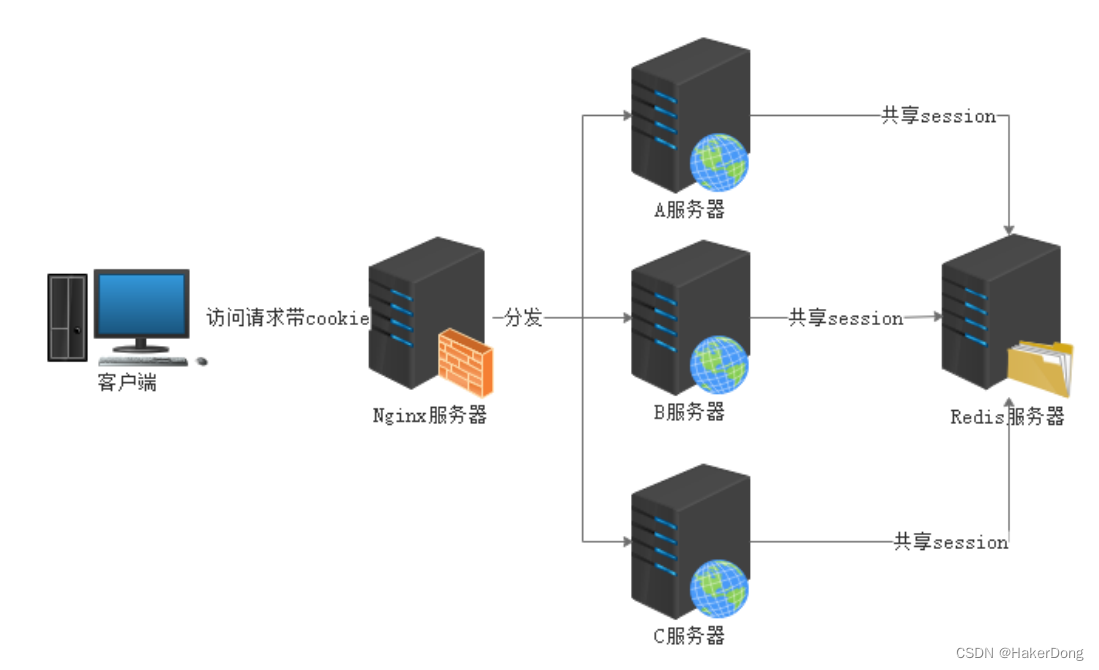
SpringBoot--中间件技术-4:整合Shiro,Shiro基于会话SessionManager实现分布式认证,附案例含源代码!
SpringBoot整合安全中间件Shiro 技术栈:SpringBootShiro 代码实现 pom文件加坐标 Springboot版本选择2.7.14 ;java版本1.8 ; shiro做了版本锁定 1.3.2 <properties><java.version>1.8</java.version><!--shiro版本锁定…...

【QT基础入门】QT中的容器类
QT中有多种容器类,它们可以用来存储和操作不同类型的数据。根据容器的特性和用途,可以分为以下几类: 序列容器 这些容器按照一定的顺序存储数据,可以通过下标或迭代器访问。QT中的序列容器有: QList: 这是最通用的序列容器,它在内部实现为一个数组列表,可以快速地在头…...
IDEA没有Add Framework Support解决办法
点击File—>Settings 点击第一个设置快捷键 点击apply和ok即可 我们要点击一下项目,再按快捷键ctrlk 即可...
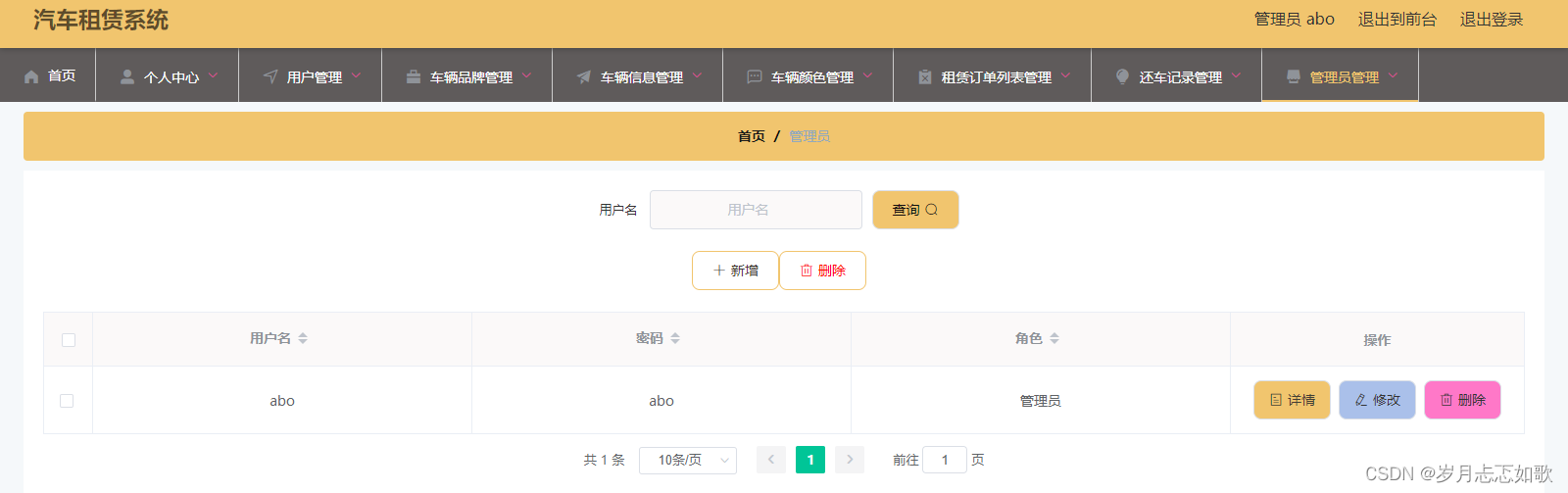
《009.SpringBoot之汽车租赁系统》
《009.SpringBoot之汽车租赁系统》 项目简介 [1]本系统涉及到的技术主要如下: 推荐环境配置:DEA jdk1.8 Maven MySQL 前后端分离; 后台:SpringBootMybatisPlus; 前台:Layuivue; [2]功能模块展示: 前端门户 1.登录&a…...
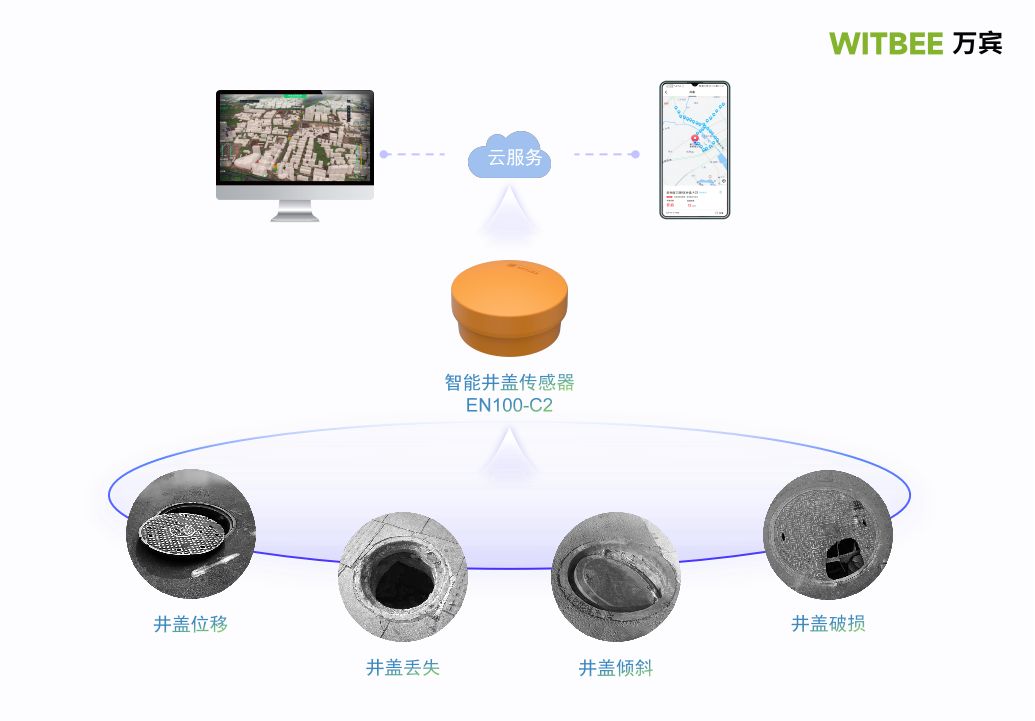
第四代智能井盖传感器,万宾科技助力城市安全
在迈向更为智能化、相互联系更为紧密的城市发展过程中,智能创新产品无疑扮演了一种重要的角色。智能井盖传感器作为新型科学技术产物,不仅解决传统井盖管理难的问题,也让城市变得更加安全美好,是城市生命线的一层重要保障。这些平…...

ClickHouse 面试题
文章目录 什么是 ClickHouse?ClickHouse 有哪些应用场景?ClickHouse 列式存储的优点有哪些?ClickHouse 的缺点是是什么?ClickHouse 的架构是怎样的?ClickHouse 的逻辑数据模型?ClickHouse 的核心特性&#…...

Python代码运行速度提升技巧!Python远比你想象中的快~
文章目录 前言一、使用内置函数二、字符串连接 VS join()三、创建列表和字典的方式四、使用 f-Strings五、使用Comprehensions六、附录- Python中的内置函数总结关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项…...
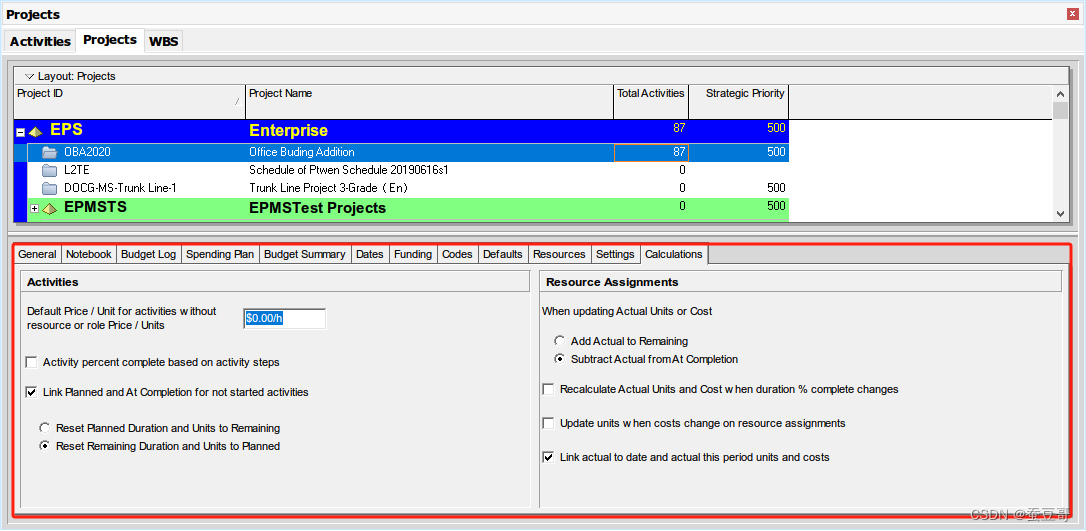
P6入门:项目初始化11-项目详情之计算Calculations
前言 使用项目详细信息查看和编辑有关所选项目的详细信息,在项目创建完成后,初始化项目是一项非常重要的工作,涉及需要设置的内容包括项目名,ID,责任人,日历,预算,资金,分类码等等&…...
<MySQL> 查询数据进阶操作 -- 联合查询
目录 一、什么是笛卡尔积? 二、什么是联合查询? 三、内连接 3.1 简介 3.2 语法 3.3 更多的表 3.4 操作演示 四、外连接 4.1 简介 4.2 语法 4.3 操作演示 五、自连接 5.1 简介 5.2 自连接非必要不使用 六、子查询(嵌套查询) 6.1 简介 6.…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
