逆向-还原代码之除法 (Interl 64)
除法和32位差不多,毕竟背后的数学公式是一样的。区别只是32位的乘法需要两个寄存器来存放大数相乘的结果,而64位的不需要,一个寄存器就能存下。所以在64位的环境下,多了右移32位这条指令,其他指令一样。

//code
#include <stdio.h>
void i_c_c()
{
int num = 1234;
int bit = 0;
bit = num / 1000;
printf("bit = %d %d\n", bit, 1234 % 1000); // 1 234
}
int main()
{
i_c_c();
return 0;
}
// asm
#include <stdio.h>
void i_c_c()
{
/*1149: f3 0f 1e fa endbr64
114d: 55 push %rbp
114e: 48 89 e5 mov %rsp,%rbp
1151: 48 83 ec 10 sub $0x10,%rsp
1155: c7 45 f8 d2 04 00 00 movl $0x4d2,-0x8(%rbp)*/
int a = 1234;
/*115c: c7 45 fc 00 00 00 00 movl $0x0,-0x4(%rbp)*/
int b = 0;
/*1163: 8b 45 f8 mov -0x8(%rbp),%eax // eax = 1234
1166: 48 63 d0 movslq %eax,%rdx // rdx = 1234
1169: 48 69 d2 d3 4d 62 10 imul $0x10624dd3,%rdx,%rdx // rdx = 1234*274877907 =339199337238 = 0x4E F9DB 2316
1170: 48 c1 ea 20 shr $0x20,%rdx // rdx = 0x4E
1174: c1 fa 06 sar $0x6,%edx // edx = 1 (2^38)/274877907 = 999.9999 = 1000
1177: c1 f8 1f sar $0x1f,%eax // eax = 0
117a: 29 c2 sub %eax,%edx // edx = 1
117c: 89 d0 mov %edx,%eax // edx = 1
117e: 89 45 fc mov %eax,-0x4(%rbp)*/
b = a / 1000;
/*1181: 8b 45 fc mov -0x4(%rbp),%eax // eax = 1
1184: ba ea 00 00 00 mov $0xea,%edx // edx = 0xea
1189: 89 c6 mov %eax,%esi
118b: 48 8d 3d 72 0e 00 00 lea 0xe72(%rip),%rdi # 2004 <_IO_stdin_used+0x4>
1192: b8 00 00 00 00 mov $0x0,%eax
1197: e8 b4 fe ff ff callq 1050 <printf@plt>*/
printf("%d %d\n", b, 0xea);
/*119c: 90 nop
119d: c9 leaveq
119e: c3 retq */
}
int main()
{
/*119f: f3 0f 1e fa endbr64
11a3: 55 push %rbp
11a4: 48 89 e5 mov %rsp,%rbp
11a7: b8 00 00 00 00 mov $0x0,%eax
11ac: e8 98 ff ff ff callq 1149 <i_c_c>*/
i_c_c();
/*11b1: b8 00 00 00 00 mov $0x0,%eax
11b6: 5d pop %rbp
11b7: c3 retq
11b8: 0f 1f 84 00 00 00 00 nopl 0x0(%rax,%rax,1)
11bf: 00 */
return 0;
}
相关文章:

逆向-还原代码之除法 (Interl 64)
除法和32位差不多,毕竟背后的数学公式是一样的。区别只是32位的乘法需要两个寄存器来存放大数相乘的结果,而64位的不需要,一个寄存器就能存下。所以在64位的环境下,多了右移32位这条指令,其他指令一样。 //code #incl…...

Python WebDriver自动化测试
Webdriver Selenium 是 ThroughtWorks 一个强大的基于浏览器的开源自动化测试工具,它通常用来编写 Web 应用的自动化测试。 Selenium 2,又名 WebDriver,它的主要新功能是集成了 Selenium 1.0 以及 WebDriver(WebDriver 曾经是…...
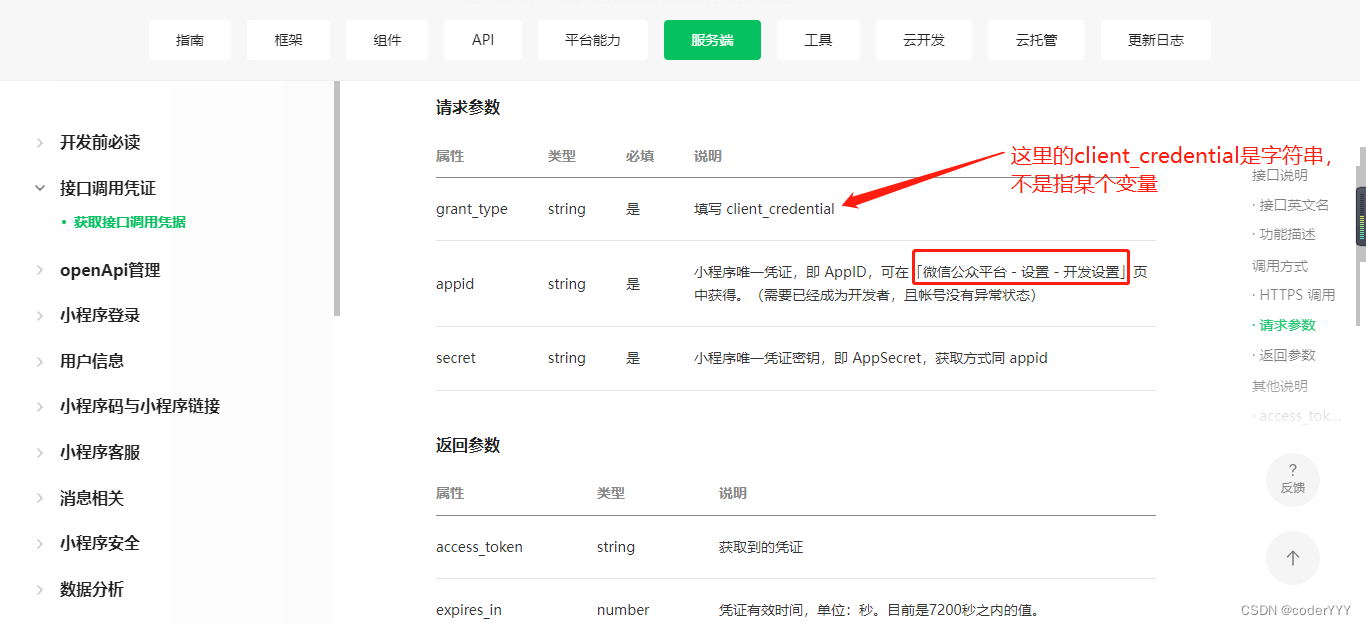
2023年微信小程序获取手机号授权登录注册详细教程,包含服务端教程
前言 小程序中有很多地方都会用到用户的手机号,比如登陆注册,填写收货地址等等。有了这个组件可以快速获取微信绑定手机号码,无须用户填写。网上大多数教程还是往年的,而微信官方的api已做了修改。本篇文章将使用最新的方法获取手…...
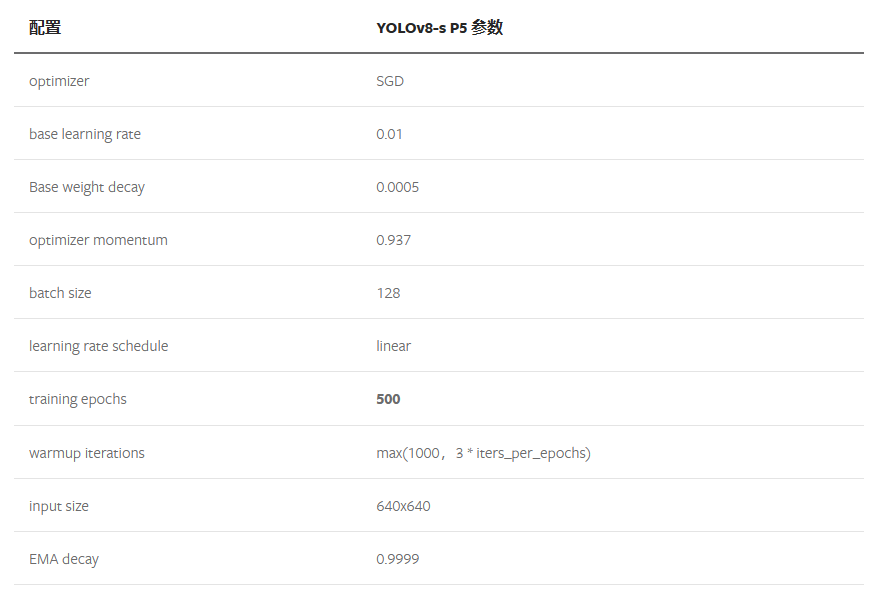
YOLOv8模型学习笔记
在前面的章节中博主学习了YOLOv5的相关知识,从YOLOv5的数据增强处理到模型设计,从正负样本匹配策略到LOSS设计,今天博主学习的是YOLOv8,同为ultralytics公司的产品,两者无论是思想层面还是具体的设计方面都有着异曲同工…...

Java SE知识点1
一、continue、break、和return的区别是什么? 在循环结构中,当循环条件不满足或者循环次数达到要求时,循环会正常结束。但是,有时候可能需要 在循环的过程中,当发生了某种条件之后 ,提前终止循环,这就需要用到下面几个关键词: 1. continue :指跳出当前的这一次循环,…...

华为OD机试模拟题 用 C++ 实现 - 端口合并(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明端口合并题目输入输出示例一输入输出说明示例二输入输出说明示例三输入输出说明...

C++ Primer Plus 第6版 读书笔记(3) 第3章 处理数据
目录 3.1 简单变量 3.1.1 变量名 *位与字节 3.1.4 无符号类型 3.1.7 C如何确定常量的类型 C是在 C 语言基础上开发的一种集面向对象编程、泛型编程和过程化编程于一体的编程语言,是C语言的超集。本书是根据2003年的ISO/ANSI C标准编写的,通过大量短…...

ArrayList源码解读
参数 //默认初始容量private static final int DEFAULT_CAPACITY 10;//空数组(用于空实例)private static final Object[] EMPTY_ELEMENTDATA {};//用于默认大小空实例的共享空数组private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA {};//保存数据的数组tra…...
)
python实战应用讲解-【语法高级篇】时间与日期(附python示例代码)
目录 保持时间、计划任务和启动程序 time 模块 time.time() 函数 time.sleep() 函数 Python3 日期和时间...
D. Moscow Gorillas(双指针 + 区间分析)
Problem - D - Codeforces 在冬天,莫斯科动物园的居民非常无聊,尤其是大猩猩。你决定娱乐他们,带了一个长度为n的排列p到动物园。长度为n的排列是由n个从1到n的不同整数以任意顺序组成的数组。例如,[2,3,1,5,4]是一个排列…...

华为OD机试题,用 Java 解【相同数字的积木游戏 1】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

Python实现GWO智能灰狼优化算法优化BP神经网络分类模型(BP神经网络分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。1.项目背景灰狼优化算法(GWO),由澳大利亚格里菲斯大学学者 Mirjalili 等人于2014年提出来的一种群智能优…...

无线蓝牙耳机哪个牌子好?2023质量好的无线蓝牙耳机推荐
近几年,随着蓝牙技术的不断进步,使用蓝牙耳机的人也越来越多。蓝牙耳机的出现,不仅能让我们摆脱线带来的约束,还能提升我们学习和工作的效率。最近看到很多人问,无线蓝牙耳机哪个牌子好?下面,我…...

Qt之QTableView自定义排序/过滤(QSortFilterProxyModel实现,含源码+注释)
一、效果示例图 1.1 自定义表格排序示例图 本文过滤条件为行索引取余2等于0时返回true,且从下图中可以看到,奇偶行是各自挨在一起的。 1.2 自定义表格过滤示例图 下图添加两列条件(当前数据大于当前列条件才返回true,且多个列…...
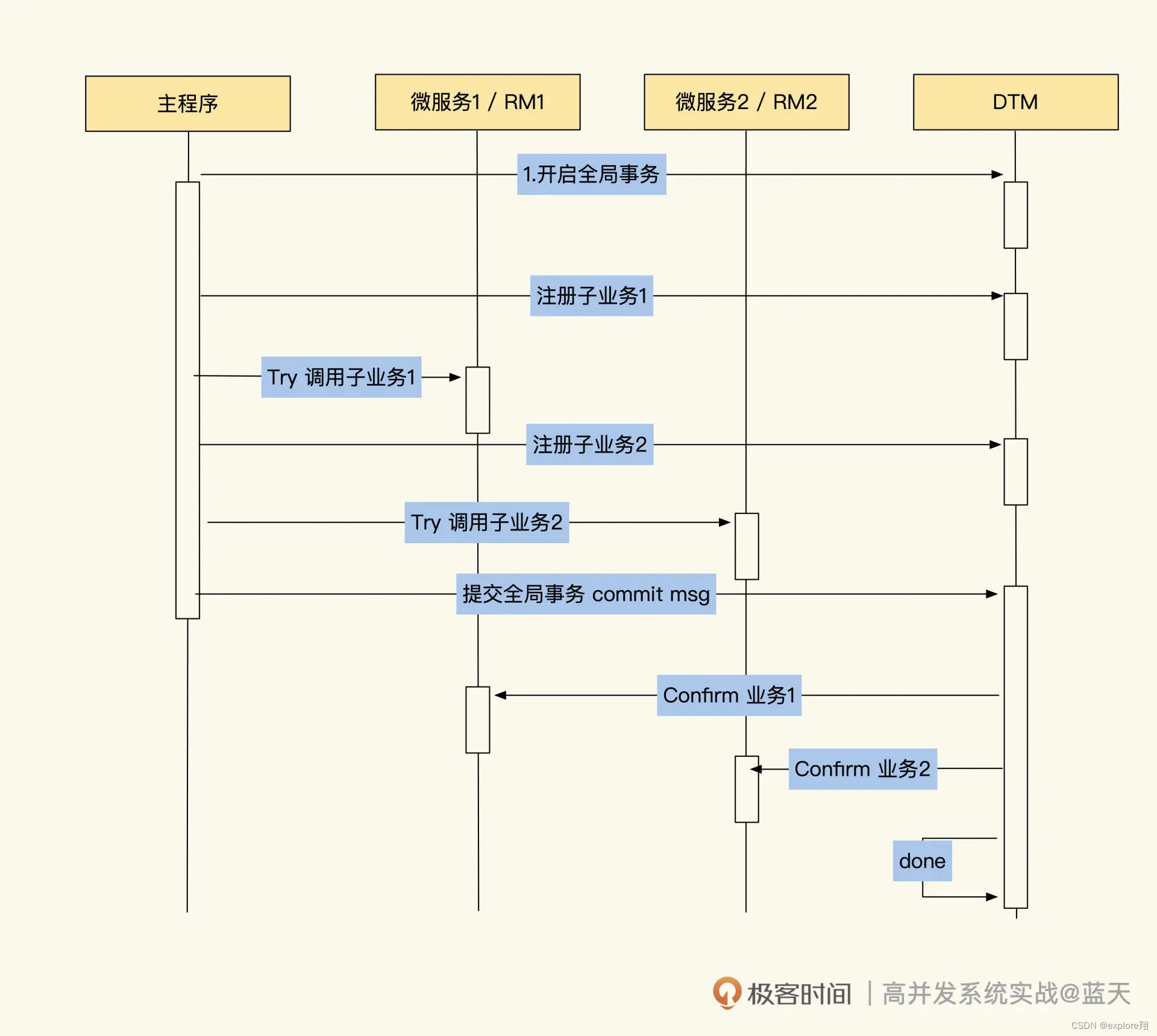
电商(强一致性系统)的场景设计
领域拆分:如何合理地拆分系统? 一般来说,强一致性的系统都会牵扯到“锁争抢”等技术点,有较大的性能瓶颈,而电商时常做秒杀活动,这对系统的要求更高。业内在对电商系统做改造时,通常会从三个方面…...
)
算法与数据结构(一)
一、时间复杂度 一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。 时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,这个算法流程中,发生了多…...

【Python】元组如何创建?
嗨害大家好鸭!我是小熊猫~ Python 元组 Python 的元组与列表类似, 不同之处在于元组的元素不能修改。 元组使用小括号,列表使用方括号。 元组创建很简单,只需要在括号中添加元素, 并使用逗号隔开即可。 如下实例…...

qt操作文件以及字符串转换
//从文件加载英文属性与中文属性对照表QFile file(":/propertyname.txt");if (file.open(QFile::ReadOnly)) {//QTextStream方法读取速度至少快百分之30#if 0while(!file.atEnd()) {QString line file.readLine();appendName(line);}#elseQTextStream in(&file)…...
)
数组中只出现一次的两个数字(异或法思路)
题目简介 一个数组中只有2个数字只有一个,其他数字都有两个。找出这两个数字。a, b 用HashMap记录就不说了。 这里记录一下用异或的方式解决。 由于异或特性为自己异或自己为0。a^a 0;所以可以异或数组中的所有数字得出 a^b 的结果,其他相同的都消掉…...

python支持的操作系统有哪些
支持python开发环境的系统有Linux、OSX和windows,以及所有主要的操作系统中。 Linux,Linux系统是为编程而设计的,因此在大多数Linux计算机中,都默认安装了Python。编写和维护Linux的人认为会使用这种系统进行编程。要在Linux中运…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
