为什么图标的宽度总是8的倍数?
对于 Windows 上的所有图标而言,它的宽度总是8的倍数,这可不是因为人们喜欢2的幂,虽然在计算机世界,你会看到很多这样的数字,例如,1024,4096等。
在 Windows 的早期阶段,大多数显卡是单色的,如果幸运的话,可能会有一张16色的显卡。它们运作在平面视频模式(planar video mode)。现在我们想象一下,将一张位图拷贝到屏幕上,这张位图和屏幕都是平面化的。
如果目标矩形的起始坐标刚好8的倍数,则位图可以通过块拷贝指令进行复制。换句话说,如果目标矩形的坐标不是8的倍数,则你需要做很多复杂的工作来对位图进行移动,从而显示到屏幕上。
这就是窗口风格 CS_BYTEALIGNCLIENT 被创建出来的原因。当把这个风格设置到窗口上时,窗口管理器将尝试定位窗口,以便客户端矩形左上角的 X 坐标位于视频内存的完美字节边界。
如果你以 1bpp 视频模式(单色或 16 色)运行,这意味着 x 坐标是 8 的倍数。通过以这种方式定位窗口,复制到客户端矩形左上角的位图将通过快速块传输指令进行复制。
如果你查看 Windows 95 或更早版本的对话框尺寸,你会发现它们的宽度几乎总是 32 个 DLU 的倍数。由于四个水平 DLU 等于一个平均字符宽度,因此你必须将对话框宽度保持为 32 的倍数,以确保最终对话框大小是 8 的倍数。
保持位图宽度以表示确切的字节边界对于当今机器的性能非常重要。复制周围的像素块通常分三个主要步骤执行:从位图左边缘到第一个字节边界的细垂直条带,然后是位图的大部分到最后一个字节边界,最后是从最后一个字节边界到右边缘的细垂直条带。如果你睁大眼睛,你实际上可以看到这三个阶段的绘画正在发生。(就像我说的,当时的机器并没有那么快。)保持字节对齐和字节宽度意味着两个细的垂直条带的宽度为零,因此可以优化出来。
当然,在当今 32bpp 显示器的世界中,所有这些旧的设计考虑在很大程度上都是无关紧要的。
总结
最近我确实在做一些和位图有关的研究,相比上古时代的单色或16色位图,32bpp(32位的位图)在处理起来,确实十分方便和直观。你可以在脑海你直接呈现位图,不需要考虑颜色板,压缩格式等这些劳什子。
对于数学一窍不通的我来说,属实是救星一枚。
最后
Raymond Chen的《The Old New Thing》是我非常喜欢的博客之一,里面有很多关于Windows的小知识,对于广大Windows平台开发者来说,确实十分有帮助。
本文来自:《Why are icons multiples of 8 pixels in width?》

相关文章:

为什么图标的宽度总是8的倍数?
对于 Windows 上的所有图标而言,它的宽度总是8的倍数,这可不是因为人们喜欢2的幂,虽然在计算机世界,你会看到很多这样的数字,例如,1024,4096等。 在 Windows 的早期阶段,大多数显卡…...

常用的xpath
一、xpath 语法 简单看一下菜鸟教程即可 1、基本语法 XPath 使用路径表达式在 XML 文档中选取节点。节点是通过沿着路径或者 step 来选取的。 下面列出了最有用的路径表达式: 表达式描述nodename选取此节点的所有子节点。/从根节点选取(取子节点&#…...
【035】基于java的进销库存管理系统(Vue+Springboot+Mysql)前后端分离项目,附万字课设论文
1.3 系统实现的功能 本次设计任务是要设计一个超市进销存系统,通过这个系统能够满足超市进销存系统的管理及员工的超市进销存管理功能。系统的主要功能包括:首页、个人中心、员工管理、客户管理、供应商管理、承运商管理、仓库信息管理、商品类别管理、 …...

【Spark分布式内存计算框架——Spark Streaming】7. Kafka集成方式
集成方式 Spark Streaming与Kafka集成,有两套API,原因在于Kafka Consumer API有两套, 文档:http://spark.apache.org/docs/2.4.5/streaming-kafka-integration.html。 方式一:Kafka 0.8.x版本 老的Old Kafka Consum…...

如何引入elementUI
elementUI的引入完整引入按需引入完整引入 在 main.js 中写入以下内容: import Vue from ‘vue’; import ElementUI from ‘element-ui’; import ‘element-ui/lib/theme-chalk/index.css’; import App from ‘./App.vue’; Vue.use(ElementUI); new Vue({ el: ‘…...

vue3+rust个人博客建站日记4-Vditor搞定MarkDown
即然是个人博客,那么绝对不能丢给自己一个大大的输入框敷衍了事。如果真是这样,现在就可以宣布项目到此结束了。如今没人享受用输入框写博客。作为一个有追求的程序员,作品就要紧跟潮流。 后来,Markdown 的崛起逐步改变了大家的排…...
KDZD-JC软化击穿试验仪
一、概 述 KDZD-JC智能软化击穿试验仪是根据GB/T4074.6-2008和idtIEC60851-6:2004标准而设计的一种新型漆包圆线检测仪器。主要适用于固体绝缘材料(如:塑料、橡胶、层压材料、薄膜、树脂、云母、陶瓷、玻璃、绝缘漆等绝缘材料及绝缘件)在工…...

【数据结构】单链表的C语言实现--万字详解介绍
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1.链表1.1 链表的概念…...

电子科技大学软件工程期末复习笔记(七):测试策略
目录 前言 重点一览 V模型 回归测试 单元测试 集成测试 重要概念 自顶向下的集成方法 自底向上的集成方法 SMOKE方法 系统测试 验收测试 α测试 β测试 本章小结 前言 本复习笔记基于王玉林老师的课堂PPT与复习大纲,供自己期末复习与学弟学妹参考用…...

逆向-还原代码之除法 (Interl 64)
除法和32位差不多,毕竟背后的数学公式是一样的。区别只是32位的乘法需要两个寄存器来存放大数相乘的结果,而64位的不需要,一个寄存器就能存下。所以在64位的环境下,多了右移32位这条指令,其他指令一样。 //code #incl…...

Python WebDriver自动化测试
Webdriver Selenium 是 ThroughtWorks 一个强大的基于浏览器的开源自动化测试工具,它通常用来编写 Web 应用的自动化测试。 Selenium 2,又名 WebDriver,它的主要新功能是集成了 Selenium 1.0 以及 WebDriver(WebDriver 曾经是…...
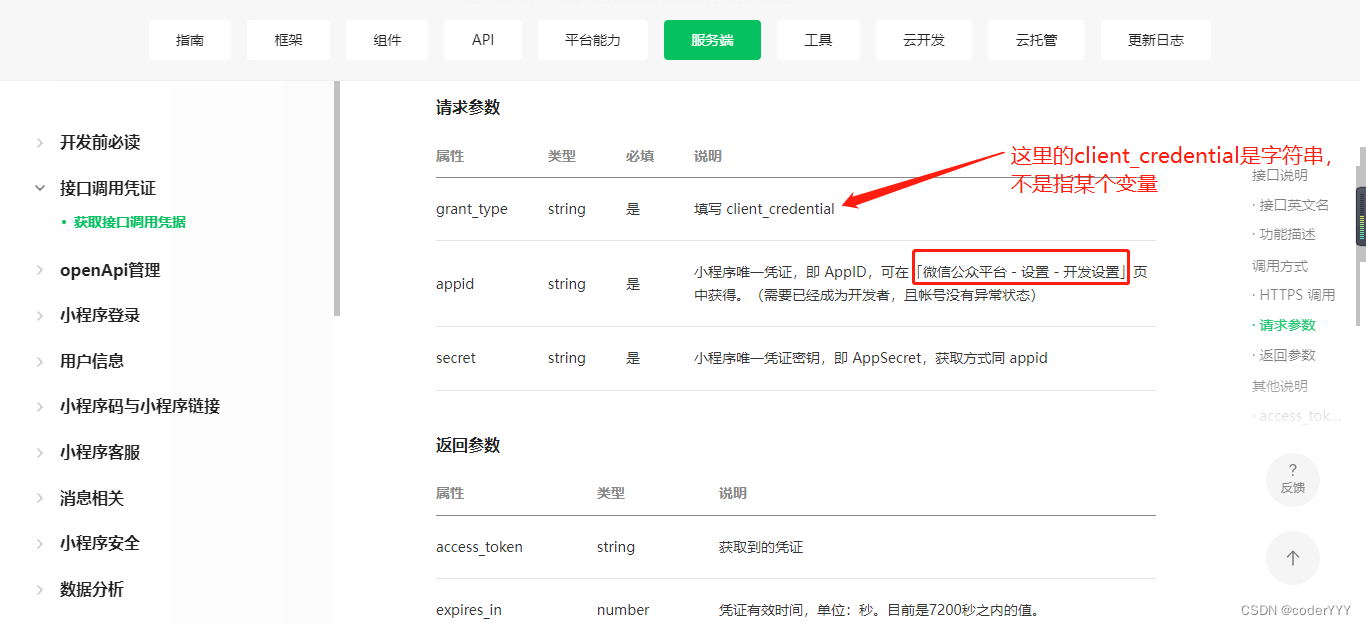
2023年微信小程序获取手机号授权登录注册详细教程,包含服务端教程
前言 小程序中有很多地方都会用到用户的手机号,比如登陆注册,填写收货地址等等。有了这个组件可以快速获取微信绑定手机号码,无须用户填写。网上大多数教程还是往年的,而微信官方的api已做了修改。本篇文章将使用最新的方法获取手…...
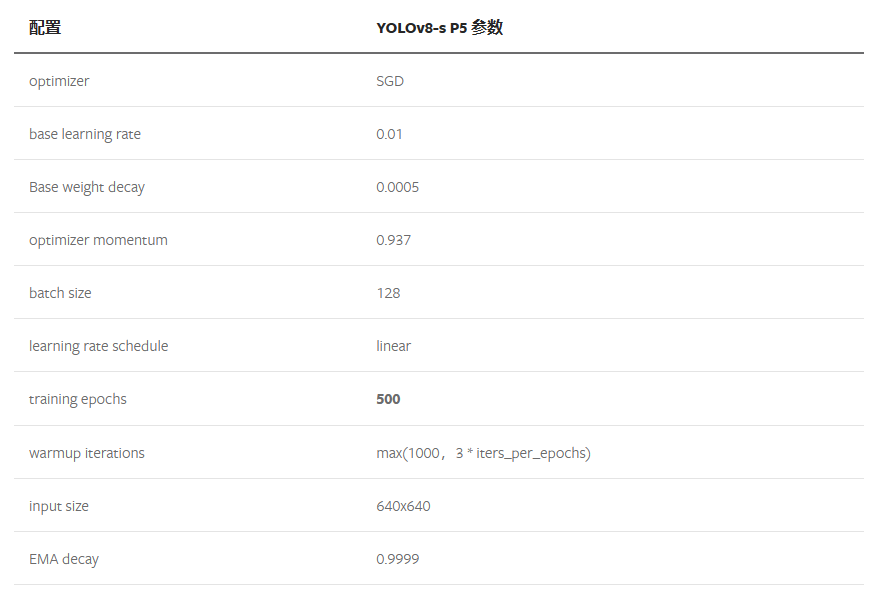
YOLOv8模型学习笔记
在前面的章节中博主学习了YOLOv5的相关知识,从YOLOv5的数据增强处理到模型设计,从正负样本匹配策略到LOSS设计,今天博主学习的是YOLOv8,同为ultralytics公司的产品,两者无论是思想层面还是具体的设计方面都有着异曲同工…...

Java SE知识点1
一、continue、break、和return的区别是什么? 在循环结构中,当循环条件不满足或者循环次数达到要求时,循环会正常结束。但是,有时候可能需要 在循环的过程中,当发生了某种条件之后 ,提前终止循环,这就需要用到下面几个关键词: 1. continue :指跳出当前的这一次循环,…...

华为OD机试模拟题 用 C++ 实现 - 端口合并(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明端口合并题目输入输出示例一输入输出说明示例二输入输出说明示例三输入输出说明...

C++ Primer Plus 第6版 读书笔记(3) 第3章 处理数据
目录 3.1 简单变量 3.1.1 变量名 *位与字节 3.1.4 无符号类型 3.1.7 C如何确定常量的类型 C是在 C 语言基础上开发的一种集面向对象编程、泛型编程和过程化编程于一体的编程语言,是C语言的超集。本书是根据2003年的ISO/ANSI C标准编写的,通过大量短…...

ArrayList源码解读
参数 //默认初始容量private static final int DEFAULT_CAPACITY 10;//空数组(用于空实例)private static final Object[] EMPTY_ELEMENTDATA {};//用于默认大小空实例的共享空数组private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA {};//保存数据的数组tra…...
)
python实战应用讲解-【语法高级篇】时间与日期(附python示例代码)
目录 保持时间、计划任务和启动程序 time 模块 time.time() 函数 time.sleep() 函数 Python3 日期和时间...
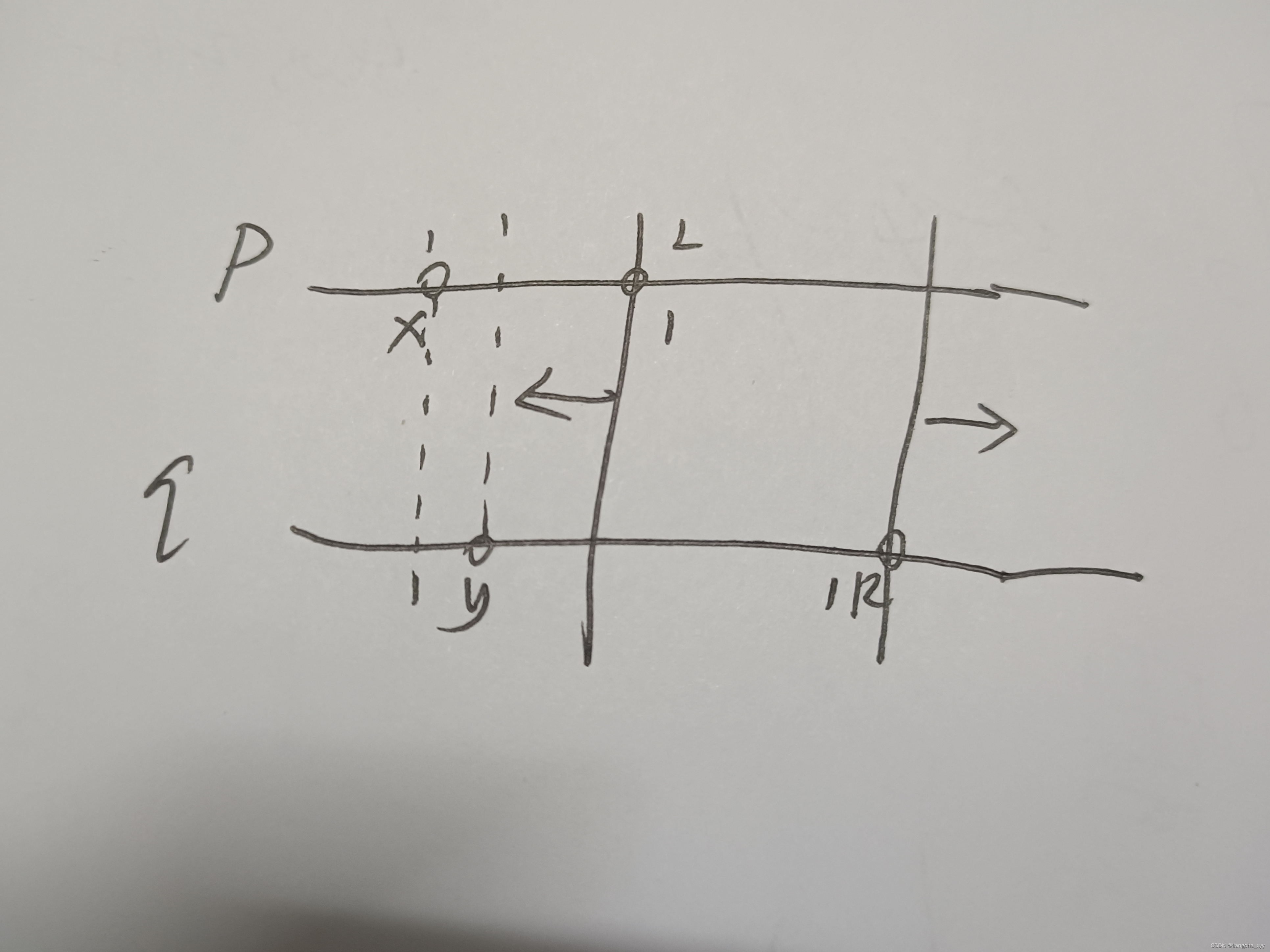
D. Moscow Gorillas(双指针 + 区间分析)
Problem - D - Codeforces 在冬天,莫斯科动物园的居民非常无聊,尤其是大猩猩。你决定娱乐他们,带了一个长度为n的排列p到动物园。长度为n的排列是由n个从1到n的不同整数以任意顺序组成的数组。例如,[2,3,1,5,4]是一个排列…...

华为OD机试题,用 Java 解【相同数字的积木游戏 1】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
