通义灵码,阿里巴巴的编程辅助工具
一、官网
通义灵码_智能编码助手_AI编程_人工智能-阿里云
二、安装VSCode
如何下载安装VSCode
三、VSCode安装通义灵码
1.访问扩展详情界面
-
方式1
访问通义灵码安装教程页面
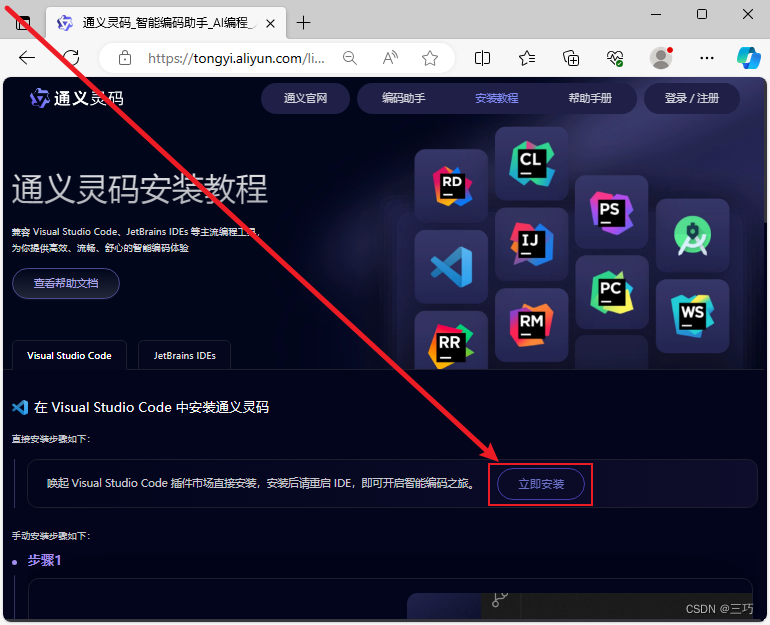
-
方法2
访问VSCode市场中的TONGYI Lingma
点击 Install 按钮访问扩展详情界面
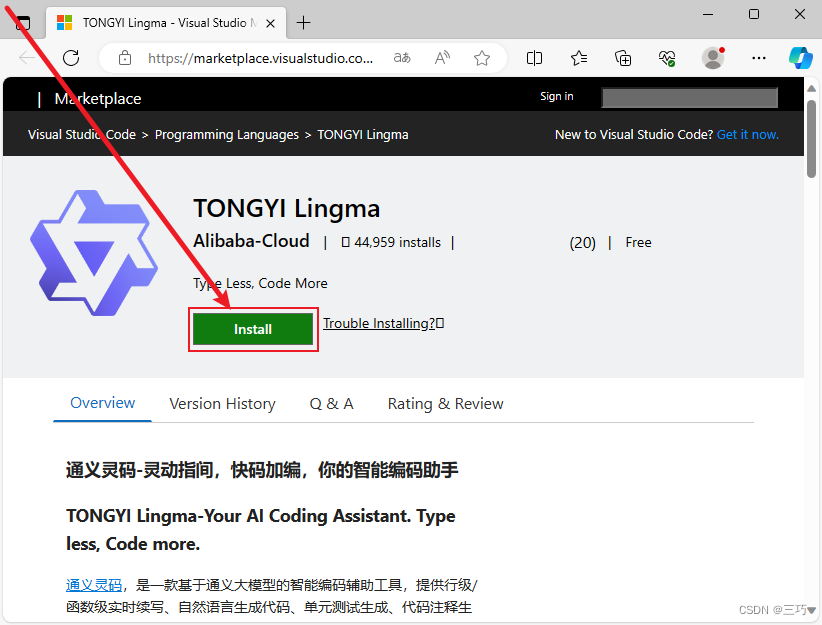
2.打开VSCode
点击打开按钮后跳转到VSCode
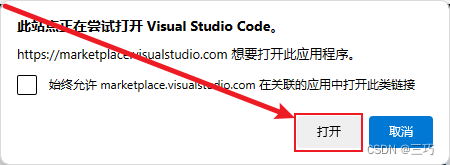
3.安装通义灵码
点击安装按钮即可
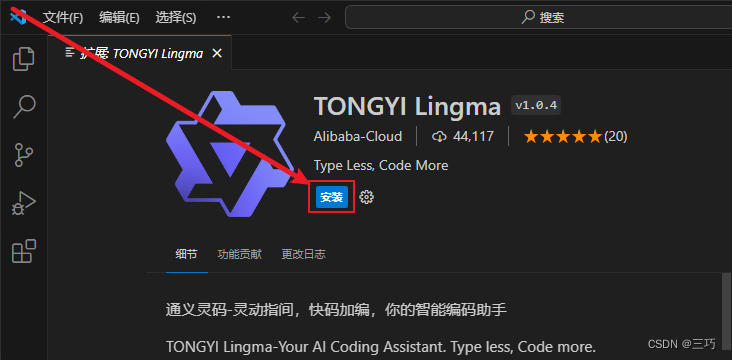
四、登录通义灵码
1.立即登录触发位置
- 安装完成后将弹出提示,点击立即登录按钮
- 如果错过通知,可以点击右下角的通义灵码图标(或者右边的铃铛图标再次打开通知)
- 点击主侧栏的通义灵码图标之后点击立即登录按钮
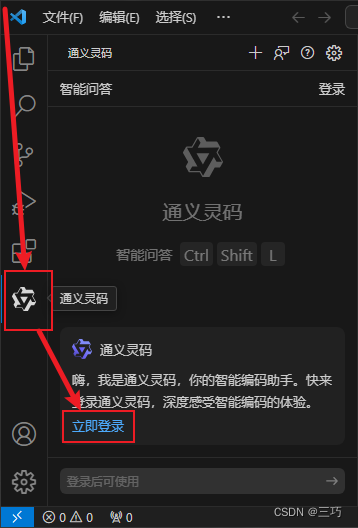
2.登录
点击同意协议按钮

弹出浏览器窗口,使用阿里云APP/支付宝/钉钉扫码,在手机上点击确认登录
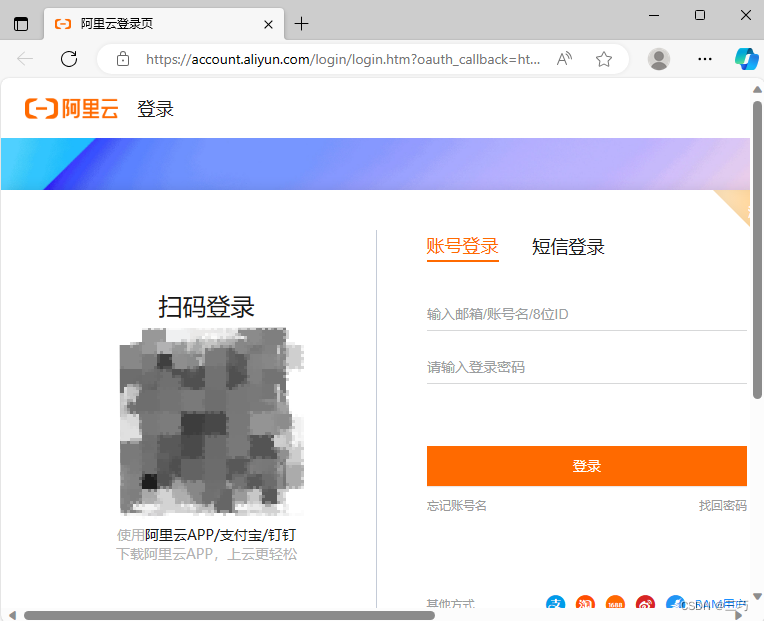
登录成功后返回VSCode即可,浏览器窗口可以关闭了
五、使用
1.代码智能生成
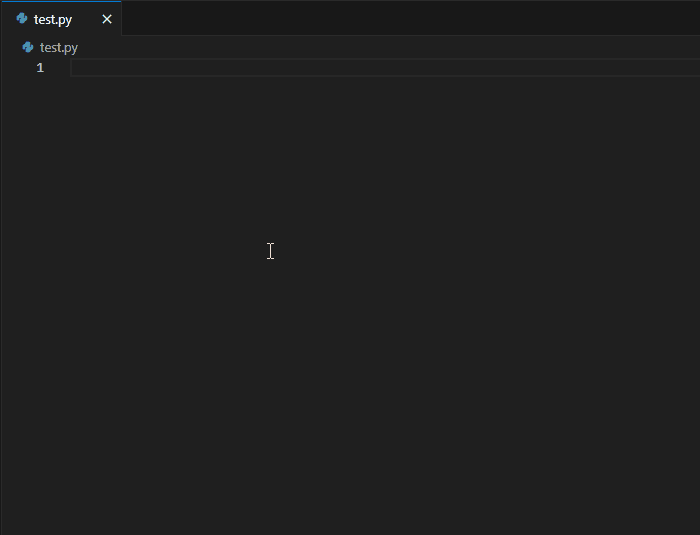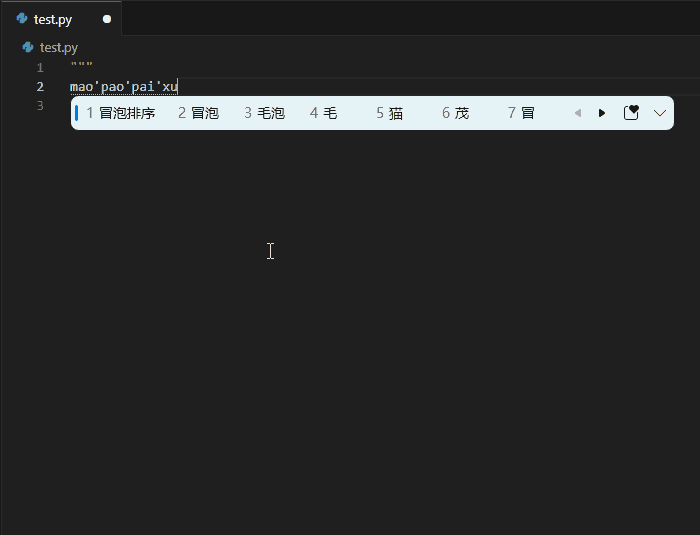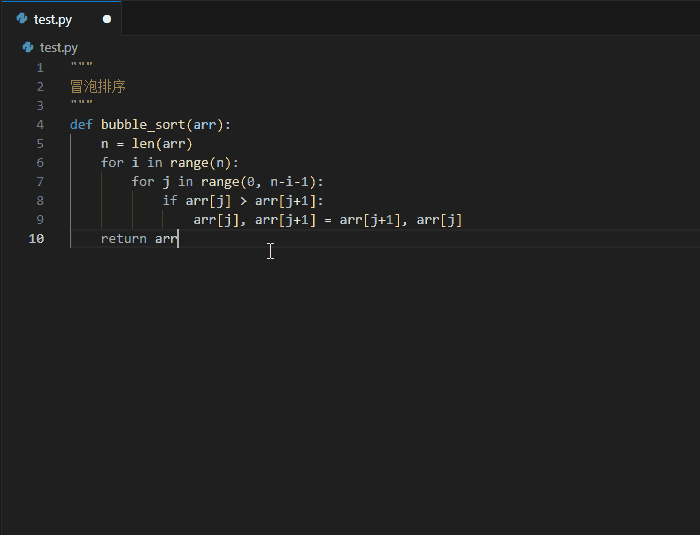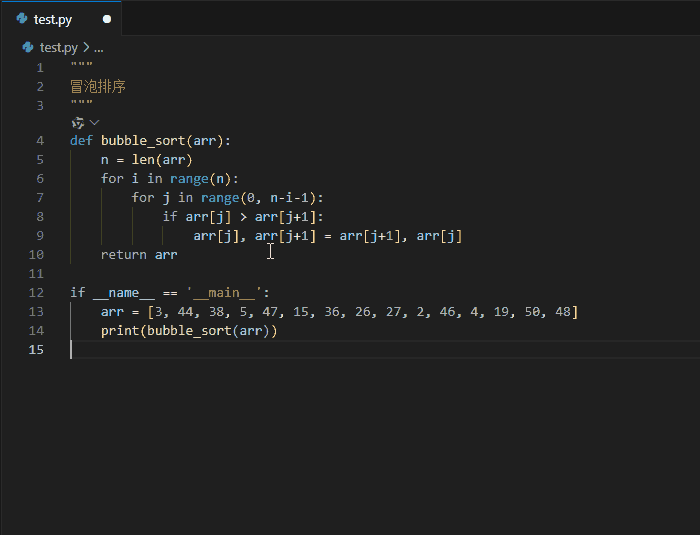
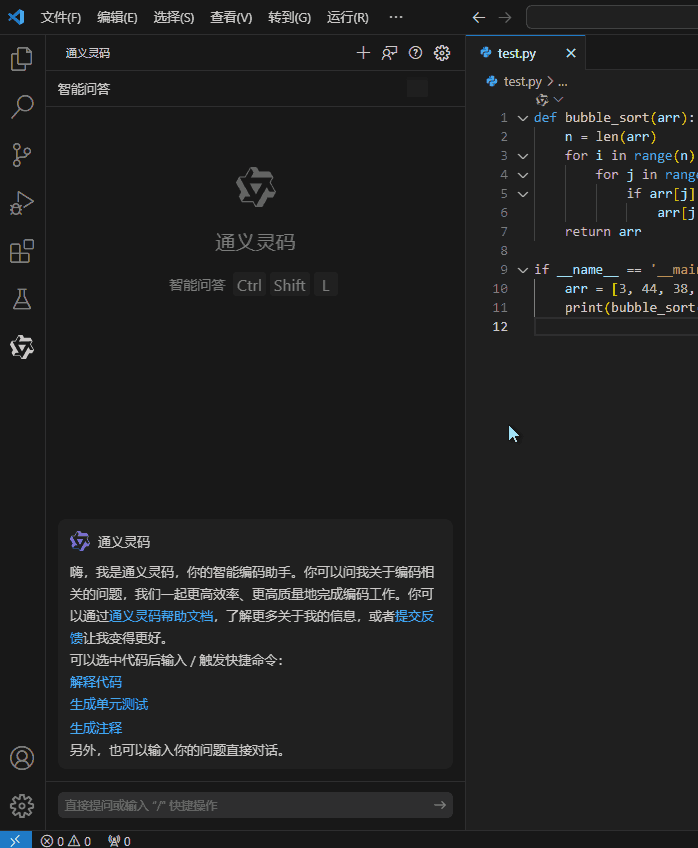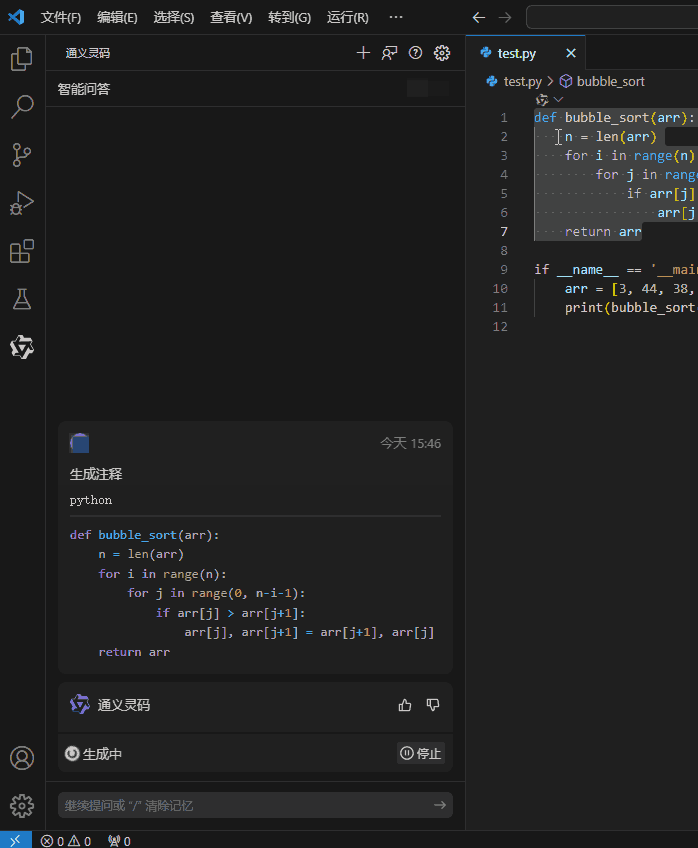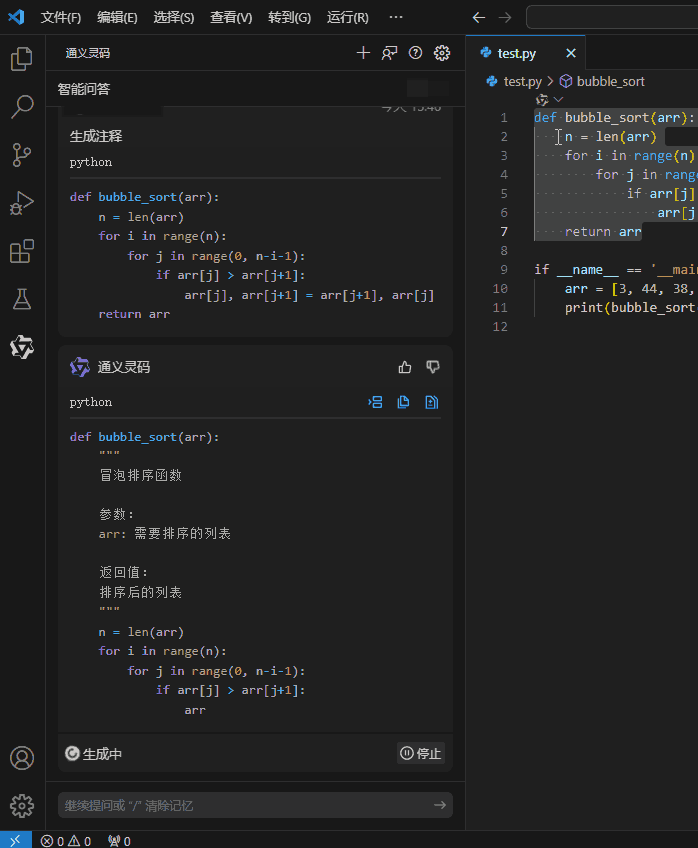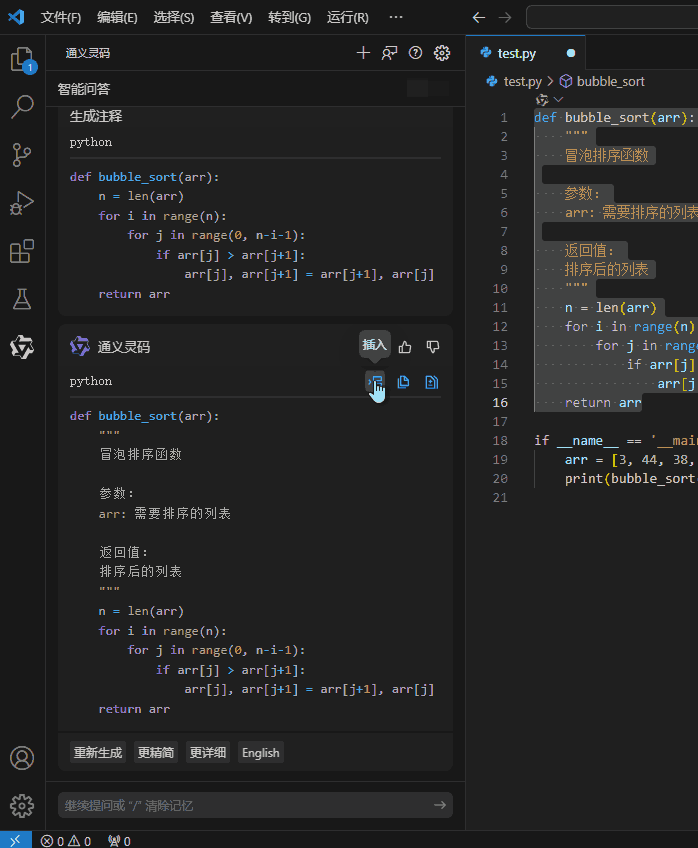
2.生成注释

相关文章:

通义灵码,阿里巴巴的编程辅助工具
一、官网 通义灵码_智能编码助手_AI编程_人工智能-阿里云 二、安装VSCode 如何下载安装VSCode 三、VSCode安装通义灵码 1.访问扩展详情界面 方式1 访问通义灵码安装教程页面 方法2 访问VSCode市场中的TONGYI Lingma 点击 Install 按钮访问扩展详情界面 2.打开VSCode …...
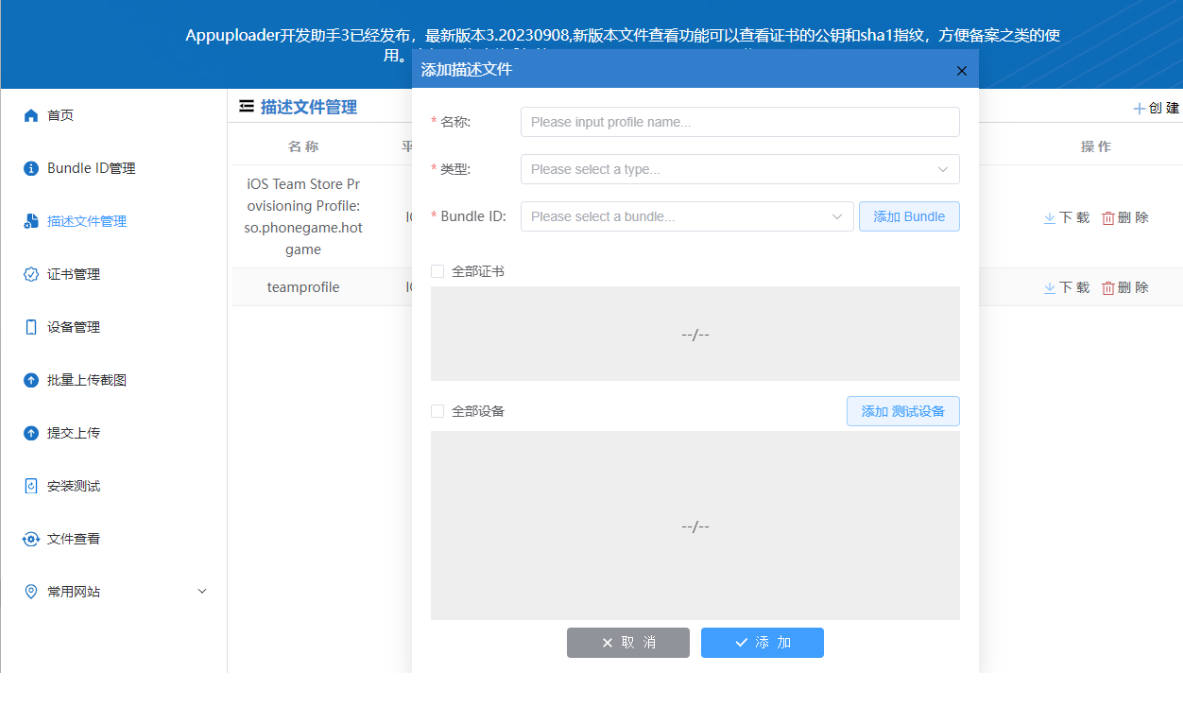
Uniapp导出的iOS应用上架详解
目录 Uniapp导出的iOS应用上架详解 摘要 引言 苹果审核标准 苹果调试 注意事项和建议 总结 摘要 本文将探讨Uniapp导出的iOS应用能否成功上架的问题。我们将从苹果审核标准、性能影响、调试流程等多个方面进行深入分析,以及向开发者提供相关注意事项和建议。…...

计算机视觉基础(7)——相机基础
前言 从这一节开始,我们来学习几何视觉。中层视觉包括相机模型、单目几何视觉、对极几何视觉和多目立体视觉等。在学习几何视觉最开始,我们先来学习一下相机模型,了解相机的基本原理,了解相机如何记录影像。 一、数字相机 1.1 基…...

解决Github上的README无法显示图片
首先感谢博主的思路:思路 最近写了点东西提交到git 发现本地能查看md里的图片用的相对路径,提交到github就看不见,并且发现不只是我自己的仓库看不见,其他人的我也看不见。那就有问题了 解决:正常使用相对路径&…...
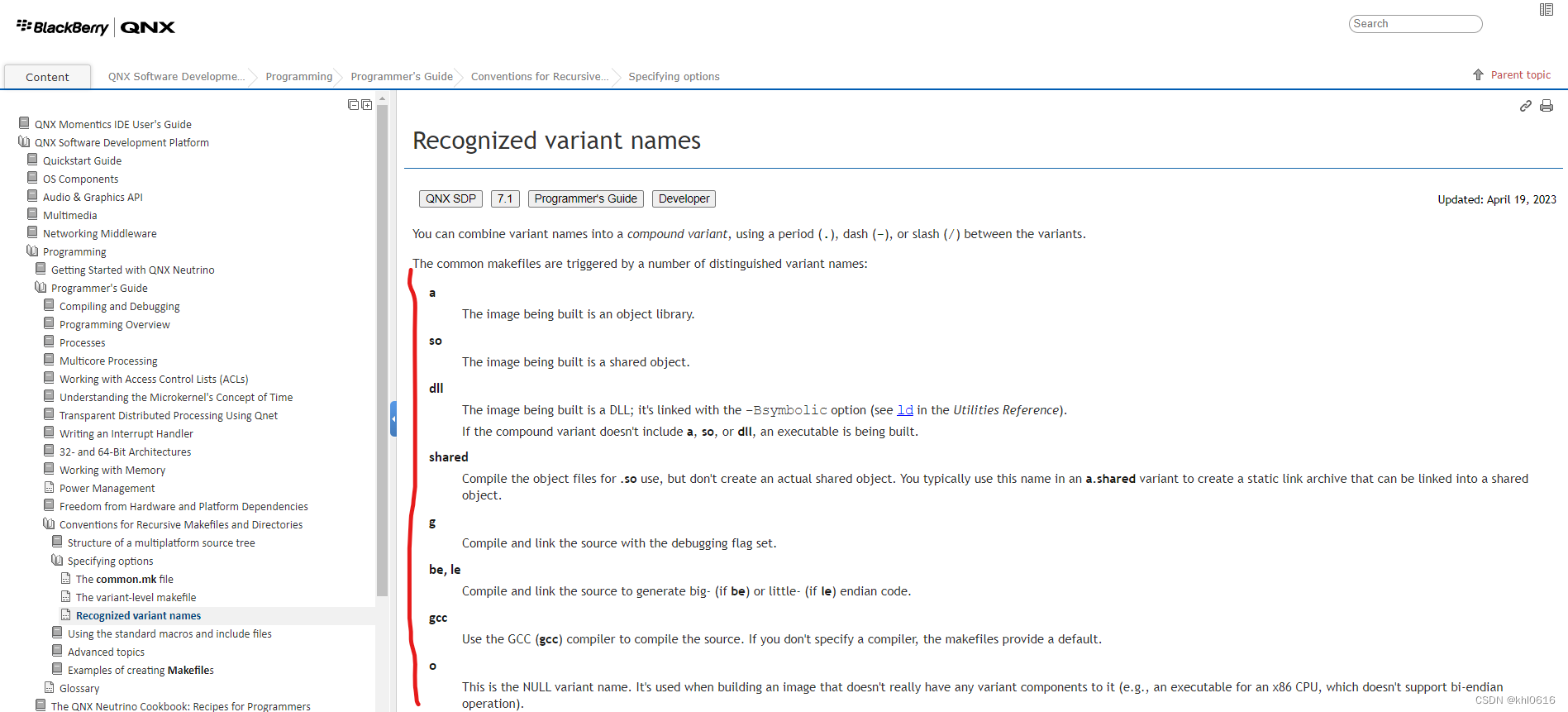
qnx 工程目录创建工具 addvariant
文章目录 前言一、addvariant 是什么二、addvariant 使用实例1. variant names 参数说明2. 创建一个可执行文件工程3. 创建一个动态库工程 总结参考资料 前言 本文主要介绍如何在qnx 开发环境中创建工程目录及其相关的配置文件(common.mk, Makefile 文件等) 软件版本ÿ…...
计算机视觉+深度学习+机器学习+opencv+目标检测跟踪+一站式学习(代码+视频+PPT)
第1章:视觉项目资料介绍与学习指南 相关知识: 介绍计算机视觉、OpenCV库,以及课程的整体结构。学习概要: 了解课程的目标和学习路径,为后续章节做好准备。重要性: 提供学生对整个课程的整体认识࿰…...

【AI视野·今日CV 计算机视觉论文速览 第278期】Mon, 30 Oct 2023
AI视野今日CS.CV 计算机视觉论文速览 Mon, 30 Oct 2023 Totally 50 papers 👉上期速览✈更多精彩请移步主页 Daily Computer Vision Papers Image Clustering Conditioned on Text Criteria Authors Sehyun Kwon, Jaeseung Park, Minkyu Kim, Jaewoong Cho, Ernest…...

深度学习:多模态与跨模态
1 定义 1.1 多模态学习 多模态学习(Multimodal Learning)是一种利用来自多种不同感官或交互方式的数据进行学习的方法。在这个语境中,“模态”指的是不同类型的数据输入,如文本、图像、声音、视频等。多模态学习的关键在于整合和…...

大数据Hadoop之——部署hadoop+hive+Mysql环境(Linux)
目录 一、JDK的安装 1、安装jdk 2、配置Java环境变量 3、加载环境变量 4、进行校验 二、hadoop的集群搭建 1、hadoop的下载安装 2、配置文件设置 2.1. 配置 hadoop-env.sh 2.2. 配置 core-site.xml 2.3. 配置hdfs-site.xml 2.4. 配置 yarn-site.xml 2.5. 配置 ma…...
在地图文档中加入图层)
Python与ArcGIS系列(四)在地图文档中加入图层
目录 0 简述1 将图层添加到地图文档中2 将图层插入到地图文档0 简述 本篇介绍如何利用arcpy实现将图层添加到地图文档中,以及将图层插入到地图文档指定的位置。 1 将图层添加到地图文档中 arcpy的mapping模块提供的AddLayer()函数可以实现将图层添加到地图文档中。功能本质上…...
QT 程序异常崩溃
出现以下问题,大概率是你在修改代码时,在pro或者pri中增加了一些不存在的头文件或者cpp,使用BeyondCmp仔细对比,分享,希望帮助到你...

Ubuntu20.04 通过nmcli命令查看网卡状态为unmanaged
问题描述: 通过下述指令查看网卡状态为 "unmanaged" nmcli dev status 解决方法: cd /usr/lib/NetworkManager/conf.d/ sudo mv 10-globally-managed-devices.conf 10-globally-managed-devices.conf.bak sudo cp 10-globally-managed-devic…...

【R Error系列】r - fatal error : RcppEigen. h:没有这样的文件或目录
在头文件那要有 // [[Rcpp::depends(RcppEigen)]] 即: #include <Rcpp.h> #include <RcppEigen.h> using namespace Rcpp; using namespace Eigen;// [[Rcpp::depends(RcppEigen)]] // [[Rcpp::export]] 参考: r - fatal error: RcppEi…...

如何在聊天记录中实时查找大量的微信群二维码
10-5 如果你有需要从微信里收到的大量信息中实时找到别人发到群里的二维码,那本文非常适合你阅读,因为本文的教程,可以让你在海量的微信消息中,实时地把二维码自动挑出来,并且帮你分类保存。 如果你是做网推的&#…...

03-CSS基础选择器
3.1 CSS基础认知🍎 3.1.1 👁️🗨️CSS概念 CSS:层叠样式表(Cascading style sheets),为网页标签增加样式表现的 语法格式: 选择器{<!-- 属性设置 -->属性名:属性值; <!--每一个…...
:main函数及编译配置详解)
【ROS】RViz2源码分析(二):main函数及编译配置详解
【ROS】郭老二博文之:ROS目录 1、main函数 #include <memory> #include <string> #include <vector>#include <QApplication>...

Vue.js的生命周期钩子
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
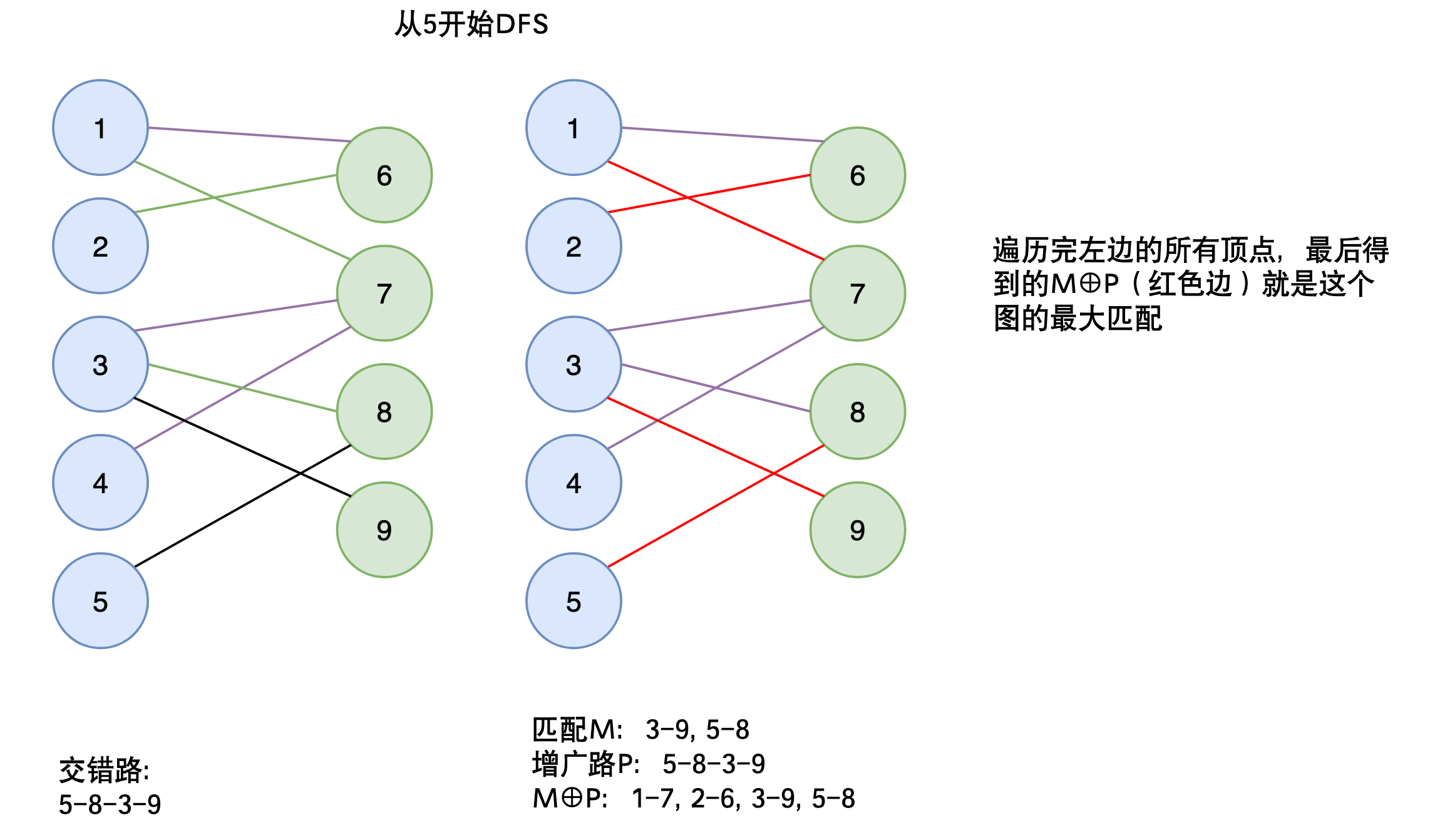
第3章:搜索与图论【AcWing】
文章目录 图的概念图的概念图的分类有向图和无向图 连通性连通块重边和自环稠密图和稀疏图参考资料 图的存储方式邻接表代码 邻接矩阵 DFS全排列问题题目描述思路回溯标记剪枝代码时间复杂度 [N 皇后问题](https://www.luogu.com.cn/problem/P1219)题目描述全排列思路 O ( n ! …...
:Qt 线程与并发)
C++ Qt 学习(七):Qt 线程与并发
1. Qt 创建线程的三种方法 1.1 方式一:派生于 QThread 派生于 QThread,这是 Qt 创建线程最常用的方法,重写虚函数 void QThread::run(),在 run() 写具体的内容,外部通过 start 调用,即可执行线程体 run() …...

Django框架之模板层
【一】Django模板系统 官方文档:官方文档 【二】常用语法 只需要记两种特殊符号: {{ }}和 {% %} 变量相关的用{逻辑相关的用{%%}。 【三】变量 在Django的模板语言中按此语法使用: {{ 变量名 }}。 当模版引擎遇到一个变量,它…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...