rabbitmq 集群搭建
RabbitMQ集群介绍
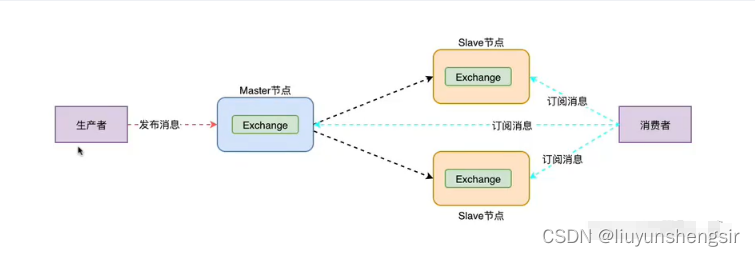
RabbitMQ集群是一组RabbitMQ节点(broker)的集合,它们一起工作以提供高可用性和可伸缩性服务。 RabbitMQ集群中的节点可以在同一物理服务器或不同的物理服务器上运行。
RabbitMQ集群的工作原理是,每个节点在一个虚拟主机中提供服务,并通过网络进行通信和数据同步。当一个节点在集群中宕机时,其他节点可以接管其未处理的消息和队列,并尝试恢复数据同步,从而确保服务的可用性。
要建立一个RabbitMQ集群,需要遵循以下步骤:
-
安装RabbitMQ:在每个节点上安装RabbitMQ。
-
配置节点:为每个节点提供唯一的名称和IP地址,并确保它们可以相互访问。
-
创建虚拟主机:在每个节点上创建相同的虚拟主机。
-
配置集群:配置每个节点以了解其他节点的存在,并让它们加入到集群中。
-
测试集群:使用工具或客户端测试集群的可用性和可靠性。
RabbitMQ集群可以显著提高应用程序的可用性和可伸缩性,但也需要注意一些方面,例如,确保网络连接的稳定性,及时修复故障节点等。
1.下载
docker pull rabbitmq:3.7.7-management
2.启动
#rabbitmqCluster01 主节点
docker run -d --hostname rabbitmq01 --name rabbitmqCluster01 -p 15672:15672 -p 5672:5672 -e RABBITMQ_ERLANG_COOKIE='rabbitmqCookie' -e RABBITMQ_DEFAULT_USER=admin -e RABBITMQ_DEFAULT_PASS=admin rabbitmq:3.7.7-management#rabbitmqCluster02 从节点
docker run -d --hostname rabbitmq02 --name rabbitmqCluster02 -p 7002:15672 -p 5673:5672 -e RABBITMQ_ERLANG_COOKIE='rabbitmqCookie' -e RABBITMQ_DEFAULT_USER=admin -e RABBITMQ_DEFAULT_PASS=admin --link rabbitmqCluster01:rabbitmq01 rabbitmq:3.7.7-management#rabbitmqCluster03 从节点
docker run -d --hostname rabbitmq03 --name rabbitmqCluster03 -p 8002:15672 -p 5674:5672 -e RABBITMQ_ERLANG_COOKIE='rabbitmqCookie' -e RABBITMQ_DEFAULT_USER=admin -e RABBITMQ_DEFAULT_PASS=admin --link rabbitmqCluster01:rabbitmq01 --link rabbitmqCluster02:rabbitmq02 rabbitmq:3.7.7-management
3.配置
rabbitmqctl stop_apprabbitmqctl reset
#rabbitmq01为rabbitmqCluster01容器中的hostname
rabbitmqctl join_cluster --ram rabbit@rabbitmq01rabbitmqctl start_app执行结果
[root@192-168-3-193 ~]# docker exec -it 0fd63626f0e6bdbe7da774f5e2a95627379976f89fe03380d5fee3ef7d1f742d bash
root@rabbitmq03:/# rabbitmqctl stop_app
Stopping rabbit application on node rabbit@rabbitmq03 ...
root@rabbitmq03:/# rabbitmqctl reset
Resetting node rabbit@rabbitmq03 ...
root@rabbitmq03:/# rabbitmqctl join_cluster --ram rabbit@rabbitmq01
Clustering node rabbit@rabbitmq03 with rabbit@rabbitmq01
root@rabbitmq03:/# rabbitmqctl start_app
Starting node rabbit@rabbitmq03 ...completed with 3 plugins.
root@rabbitmq03:/# rabbitmqctl cluster_status
Cluster status of node rabbit@rabbitmq03 ...
[{nodes,[{disc,[rabbit@rabbitmq01]},{ram,[rabbit@rabbitmq03,rabbit@rabbitmq02]}]},{running_nodes,[rabbit@rabbitmq02,rabbit@rabbitmq01,rabbit@rabbitmq03]},{cluster_name,<<"rabbit@rabbitmq01">>},{partitions,[]},{alarms,[{rabbit@rabbitmq02,[]},{rabbit@rabbitmq01,[]},{rabbit@rabbitmq03,[]}]}]
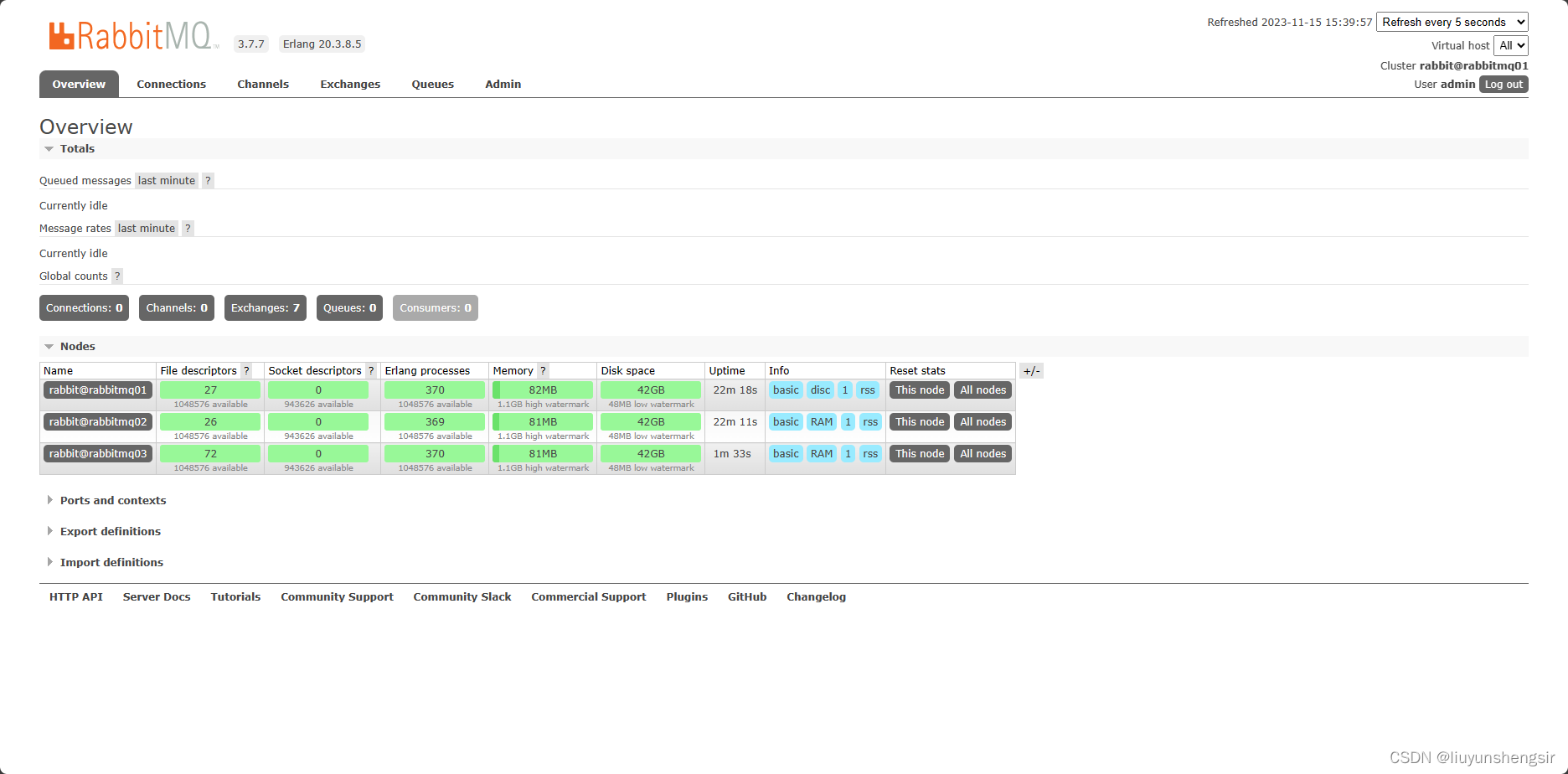
root@rabbitmq03:/#4.登录
相关文章:

rabbitmq 集群搭建
RabbitMQ集群介绍 RabbitMQ集群是一组RabbitMQ节点(broker)的集合,它们一起工作以提供高可用性和可伸缩性服务。 RabbitMQ集群中的节点可以在同一物理服务器或不同的物理服务器上运行。 RabbitMQ集群的工作原理是,每个节点在一个…...

【云原生-Kurbernets篇】Kurbernets集群的调度策略
调度 一、Kurbernetes的list-watch机制1.1 list-watch机制简介1.2 创建pod的流程(结合list-watch机制) 二、Scheduler的调度策略2.1 简介2.2 预选策略(predicate)2.3 优选策略(priorities) 三、标签管理3.1…...
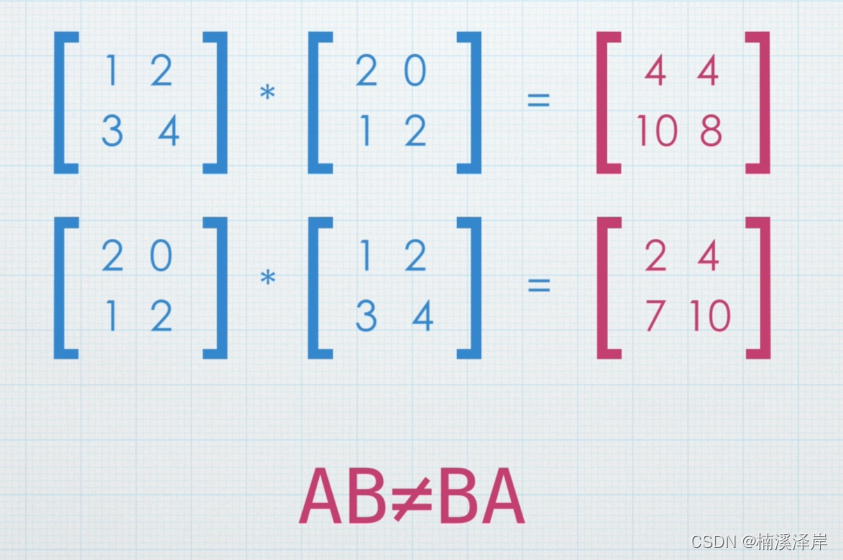
Unity中Shader矩阵的乘法
文章目录 前言一、矩阵乘以标量二、矩阵和矩阵相乘1、第一个矩阵的列数必须 与 第二个矩阵的行数相等,否则无法相乘!2、相乘的结果矩阵,行数由第一个矩阵的行数决定,列数由第二个矩阵的列数决定! 三、单位矩阵四、矩阵…...
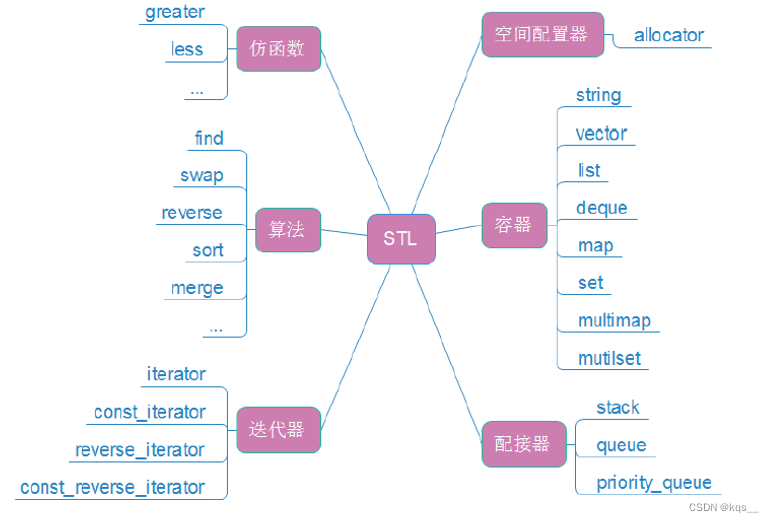
C++ STL简介
1. 什么是STL STL(standard template libaray-标准模板库):是C标准库的重要组成部分,不仅是一个可复用的组件库,而且是一个包罗数据结构与算法的软件框架。 2. STL的版本 原始版本 Alexander Stepanov、Meng Lee 在惠普实验室…...

如何优雅的使用contorller层
一个完整的后端请求由 4 部分组成: 接口地址(也就是 URL 地址)请求方式(一般就是 get、set,当然还有 put、delete)请求数据(request,有 head 跟 body)响应数据ÿ…...

发现区块链世界的新大门——AppBag.io DApp导航网站全面解析
随着区块链技术的飞速发展,分布式应用(DApp)个充满创新和可能性的领域里,appbag.io DApp导航网站应运而生,为您打开探索区块链世界的新大门。 区块链应用的集大成者 AppBag.io DApp导航网站不仅是一个DApp的集散地&a…...

C#多线程Thread、Task
在C#中,线程可以用于完成需要耗费较长时间的操作,而不会阻塞用户界面。一个程序可以有多个线程,每个线程可以并行执行代码。 在C#中,可以使用System.Threading.Thread类来创建和控制线程,使用System.Threading.Mutex类…...

Qt QWebSocket实现JS调用C++
目录 前言1、QWebChannel如何与网页通信2、QWebSocketQWebChannel与网页通信2.1 WebSocketTransport2.2 WebSocketClientWrapper2.3 初始化WebSocket服务器2.4 前端网页代码修改 总结 前言 本篇主要介绍实现JS调用C的另一种方式,即QWebSocketQWebChannel。与之前的…...

Android Matrix的使用详解(通过矩阵获取到图片缩放比例和角度)
网上查了好久相关的资料,都没有明确的答案。最终通过多次测试结果,结合安卓定义的矩阵含义,推算出来矩阵的数学含义以及相关的计算公式 1.获取Matrix矩阵: Matrix matrix new Matrix(); float[] matrixValues new float[9]; …...
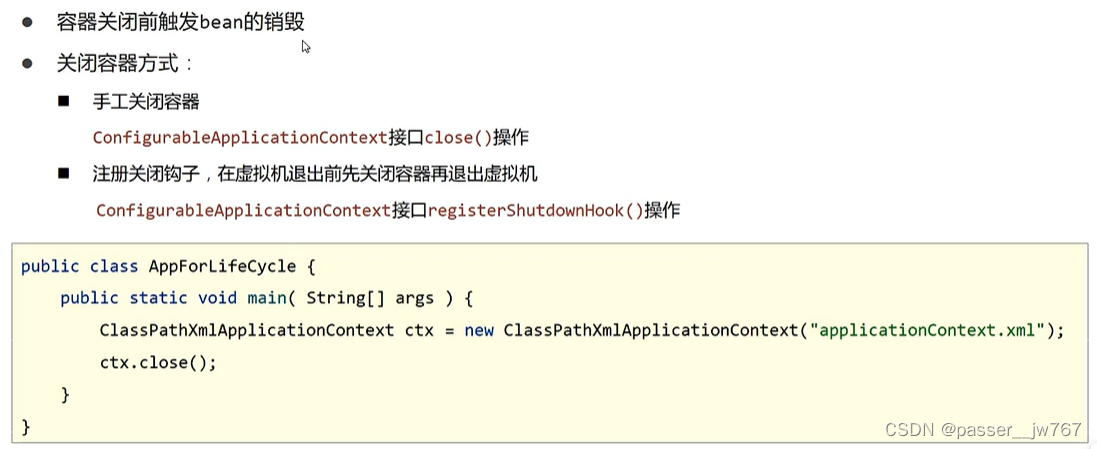
【Spring】bean的生命周期
这里写目录标题 1. 在类中提供生命周期控制方法,并在配置文件中配置init-method&destroy-method(配置)关闭容器操作1:ctx.close()关闭容器操作2:关闭钩子:ctx.registerShutdownHook() 2. 实现接口来做和…...

C#运算符重载
运算符重载允许你重新定义内置运算符(如、-、*等)的行为,以便它们可以用于自定义类型(类/结构体)。通过运算符重载,你可以为自定义类型创建更直观和灵活的操作。 在C#中,可以重载的运算符如下&…...

【L2GD】: 无环局部梯度下降
文章链接:Federated Learning of a Mixture of Global and Local Models 发表期刊(会议): ICLR 2021 Conference(机器学习顶会) 往期博客:FLMix: 联邦学习新范式——局部和全局的结合 目录 1.背景介绍2. …...
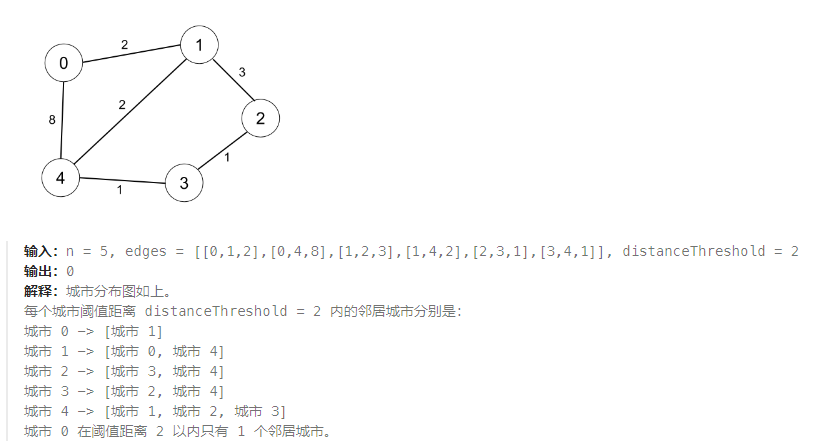
2023-11-14 LeetCode每日一题(阈值距离内邻居最少的城市)
2023-11-14每日一题 一、题目编号 1334. 阈值距离内邻居最少的城市二、题目链接 点击跳转到题目位置 三、题目描述 有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的…...

AdServices归因和iAd归因集成
AdServices framework 是 Apple 专门为 ASA 提供的归因框架 。尤其在ATT 政策推出以后,app 获取用户 IDFA 的比例大幅降低,传统的依靠IDFA 的方法也无法准确归因。 但是 Apple 为 ASA 开了一个后门,其他广告渠道无法获取用户的 IDFA 作为身份…...
关于 内部类 你了解多少?(详解!!)
目录 1. 什么是内部类? 2. 内部类的分类 3. 内部类 3.1 实例内部类 3.2 静态内部类 4. 局部内部类 5. 匿名内部类 6.对象的打印 “不积跬步无以至千里,不积小流无以成江海。”每天坚持学习,哪怕是一点点!!&a…...
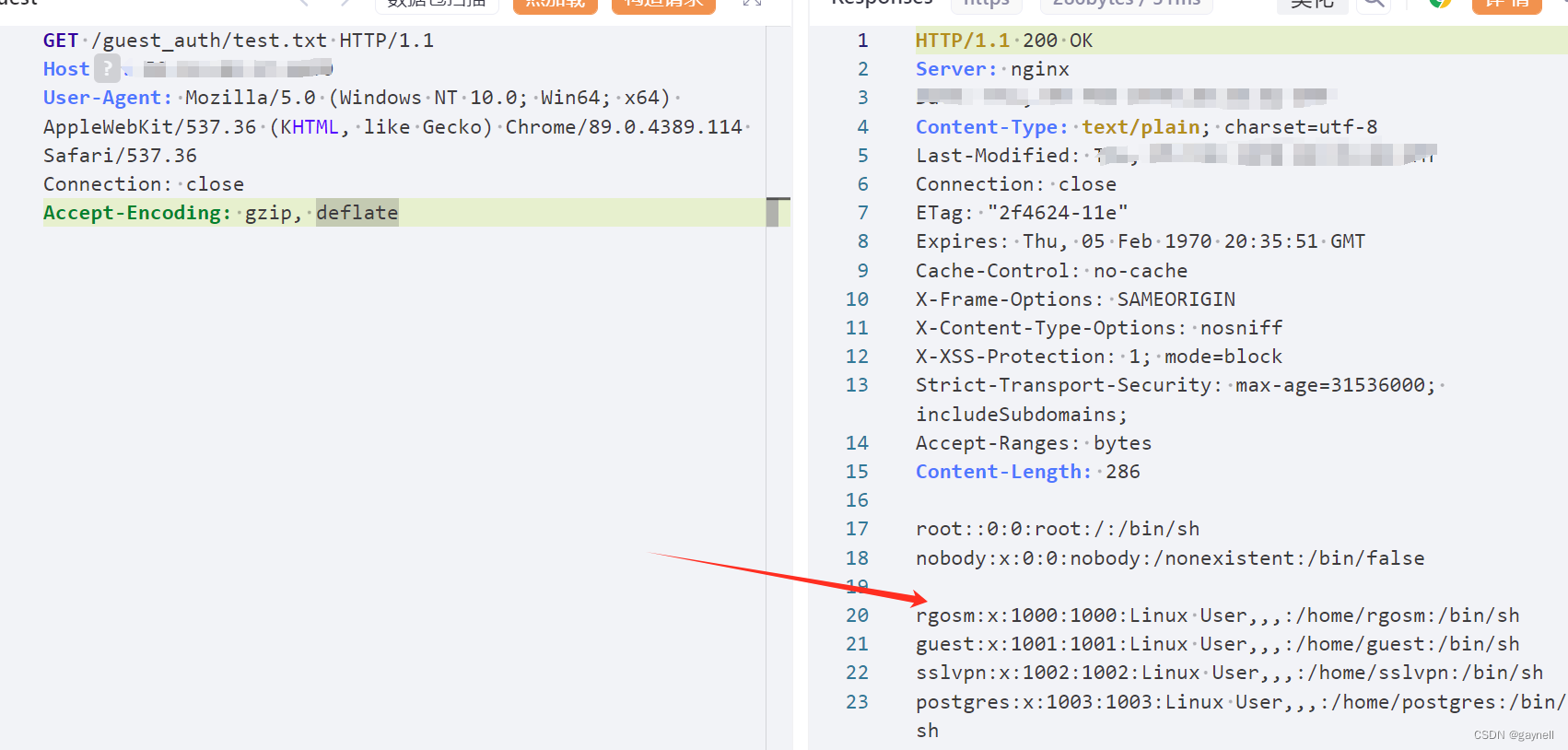
CNVD-2021-09650:锐捷NBR路由器(guestIsUp.php)RCE漏洞复现 [附POC]
文章目录 锐捷NBR路由器guestIsUp.php远程命令执行漏洞(CNVD-2021-09650)复现 [附POC]0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 锐捷NBR路由器guestIsUp.php远程命令执行漏洞(CNVD-2021-09650)复现 [附POC] 0x01 前言 免…...
如何在Docker部署Draw.io绘图工具并远程访问
文章目录 前言1. 使用Docker本地部署Drawio2. 安装cpolar内网穿透工具3. 配置Draw.io公网访问地址4. 公网远程访问Draw.io 前言 提到流程图,大家第一时间可能会想到Visio,不可否认,VIsio确实是功能强大,但是软件为收费࿰…...

Android APK打包的过程主要步骤
Android APK打包的过程可以概括为以下几个主要步骤: 编译源代码:将开发好的Java源代码编译成Dalvik字节码文件(.dex文件),Android安卓该文件包含了Android平台上的运行程序的指令集。打包资源文件:将应用程…...
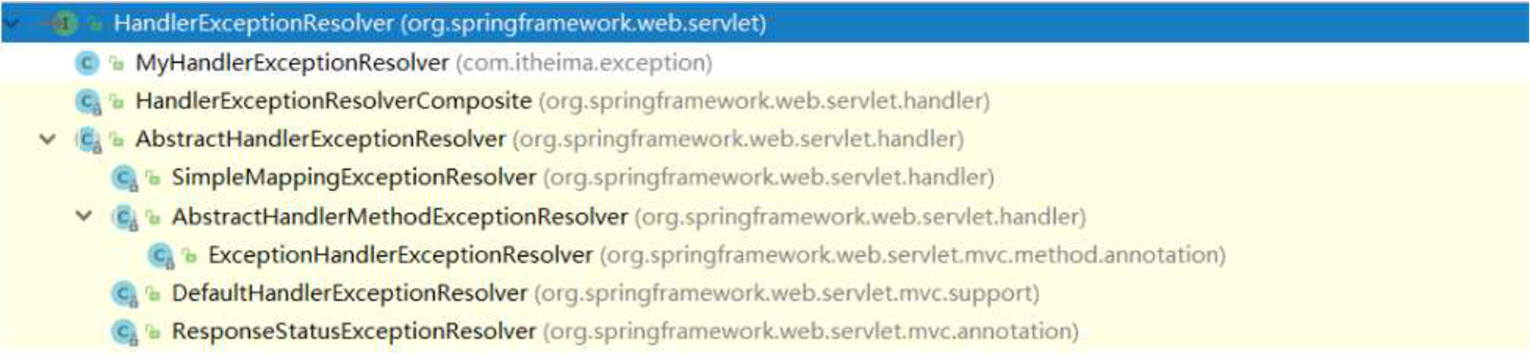
吃透 Spring 系列—MVC部分
目录 ◆ SpringMVC简介 - SpringMVC概述 - SpringMVC快速入门 - Controller中访问容器中的Bean - SpringMVC关键组件浅析 ◆ SpringMVC的请求处理 - 请求映射路径的配置 - 请求数据的接收 - Javaweb常用对象获取 - 请求静态资源 - 注解驱动 标签 ◆ SpringMV…...

Java面试题(每天10题)-------连载(32)
目录 设计模式篇 1、工厂方法模式(利用创建同一接口的不同实例): 2、抽象工厂模式(多个工厂) 3、单例模式(保证对象只有一个实例) 4、原型模式(对一个原型进行复制、克隆产生类…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...
