分类预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测
分类预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测
目录
- 分类预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测
- 分类效果
- 基本描述
- 程序设计
- 参考资料
分类效果





基本描述
1.Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测,运行环境Matlab2023b及以上;
2.优化参数为:学习率,隐含层节点,正则化参数。
3.多特征输入单输出的二分类及多分类模型。程序内注释详细,直接替换数据就可以用;
程序语言为matlab,程序可出分类效果图,迭代优化图,混淆矩阵图;
4.data为数据集,输入12个特征,分四类;main为主程序,其余为函数文件,无需运行,可在下载区获取数据和程序内容。
程序设计
- 完整程序和数据获取方式:私信博主回复Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测。
function [gbest,g,Convergence_curve]=PSO(N,T,lb,ub,dim,fobj)
%% 定义粒子群算法参数
% N 种群 T 迭代次数
%% 随机初始化种群
D=dim; %粒子维数
c1=1.5; %学习因子1
c2=1.5; %学习因子2
w=0.8; %惯性权重Xmax=ub; %位置最大值
Xmin=lb; %位置最小值
Vmax=ub; %速度最大值
Vmin=lb; %速度最小值
%%
%%%%%%%%%%%%%%%%初始化种群个体(限定位置和速度)%%%%%%%%%%%%%%%%x=rand(N,D).*(Xmax-Xmin)+Xmin;
v=rand(N,D).*(Vmax-Vmin)+Vmin;
%%%%%%%%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%%%%%%%%
p=x;
pbest=ones(N,1);
for i=1:Npbest(i)=fobj(x(i,:));
end
%%%%%%%%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%%%%%%%%
g=ones(1,D);
gbest=inf;
for i=1:Nif(pbest(i)<gbest)g=p(i,:);gbest=pbest(i);end
end
%%%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%%%%%%
for i=1:Tifor j=1:N%%%%%%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%%%%%if (fobj(x(j,:))) <pbest(j)p(j,:)=x(j,:);pbest(j)=fobj(x(j,:));
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229
相关文章:

分类预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测
分类预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测 目录 分类预测 | Matlab实现PSO-BiLSTM-Attention粒子群算法优化双向长短期记忆神经网络融合注意力机制多特征分类预测分类效果基本描述程序设计参考资料 分类效果…...
【Python】Pandas(学习笔记)
一、Pandas概述 1、Pandas介绍 2008年WesMcKinney开发出的库,专门用于数据挖掘的开源python库 以Numpy为基础,借力Numpy模块在计算方面性能高的优势 基于matplotib,能够简便的画图 独特的数据结构 import pandas as pd2、Pandas优势 便…...

京联易捷科技与劳埃德私募基金管理有限公司达成合作协议签署
京联易捷科技与劳埃德私募基金管理有限公司今日宣布正式签署合作协议,双方在数字化进程、资产管理与投资以及中英金融合作方面将展开全面合作。 劳埃德(中国)私募基金管理有限公司是英国劳埃德私募基金管理有限公司的全资子公司,拥有丰富的跨境投资经验和卓越的募资能力。该集…...

Netty Review - 从BIO到NIO的进化推演
文章目录 BIODEMO 1DEMO 2小结论单线程BIO的缺陷BIO如何处理并发多线程BIO服务器的弊端 NIONIO要解决的问题模拟NIO方案一: (等待连接时和等待数据时不阻塞)方案二(缓存Socket,轮询数据是否准备好)方案二存…...
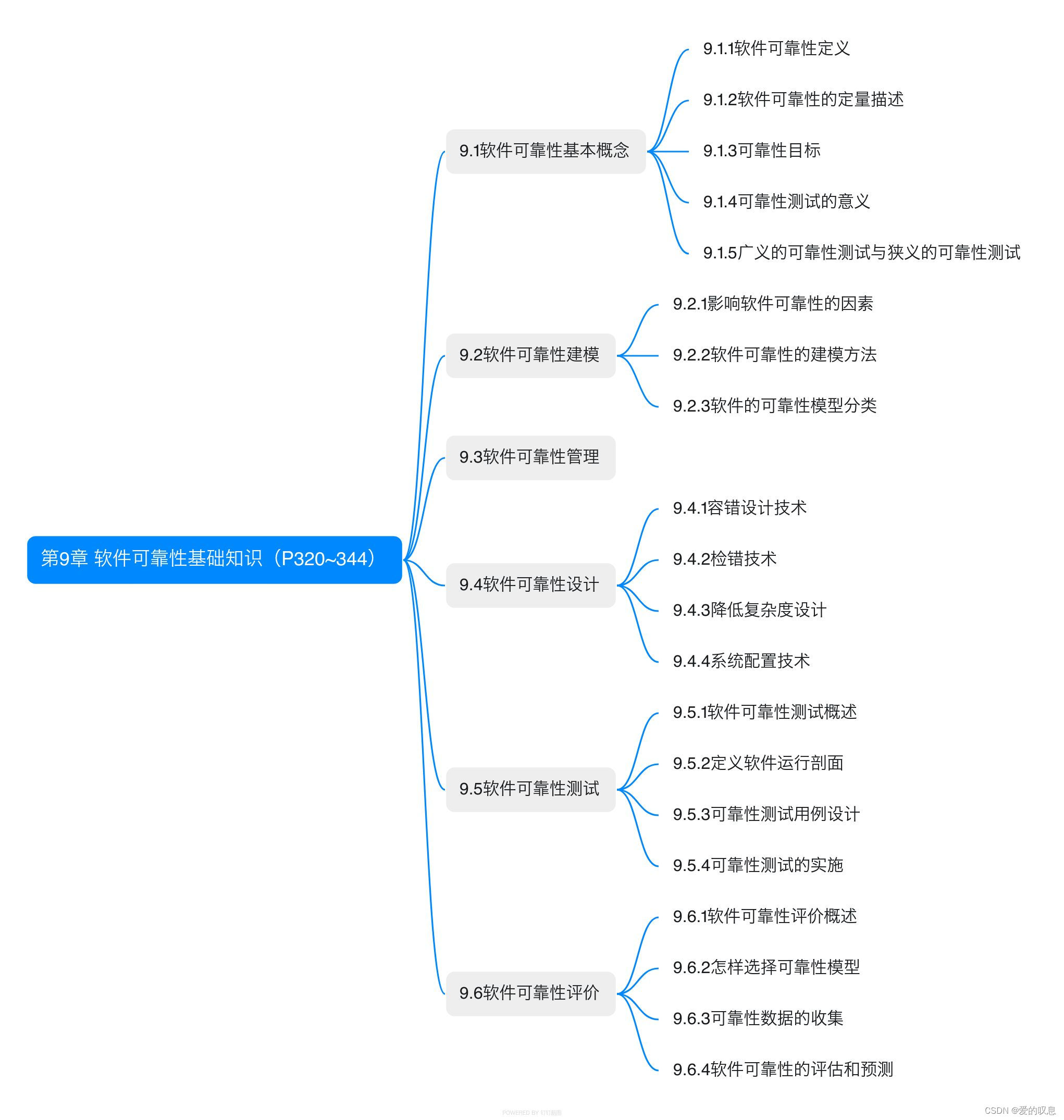
软考-高级-系统架构设计师教程(清华第2版)【第9章 软件可靠性基础知识(P320~344)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第9章 软件可靠性基础知识(P320~344)-思维导图】 课本里章节里所有蓝色字体的思维导图...
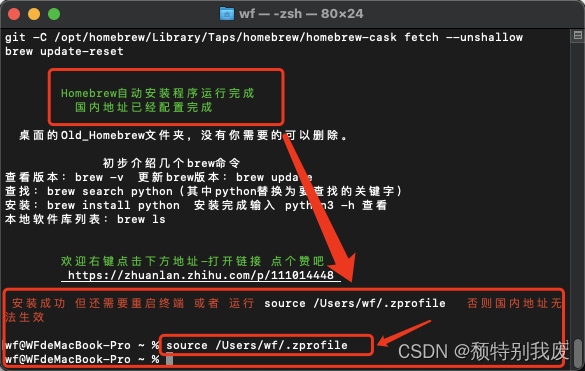
M系列 Mac安装配置Homebrew
目录 首先,验证电脑是否安装了Homebrew 1、打开终端输入以下指令: 2、如图所示,该电脑没有安装Homebrew ,下面我们安装Homebrew 一、官网下载 (不建议) 1、我们打开官网:https://brew.sh/ …...
WebRTC简介及使用
文章目录 前言一、WebRTC 简介1、webrtc 是什么2、webrtc 可以做什么3、数据传输需要些什么4、SDP 协议5、STUN6、TURN7、ICE 二、WebRTC 整体框架三、WebRTC 功能模块1、视频相关①、视频采集---video_capture②、视频编解码---video_coding③、视频加密---video_engine_encry…...

网工内推 | 国企、上市公司售前,CISP/CISSP认证,最高18K*14薪
01 中电福富信息科技有限公司 招聘岗位:售前工程师(安全) 职责描述: 1、对行业、用户需求、竞争对手等方面提出分析报告,为公司市场方向、产品研发和软件开发提供建议; 2、负责项目售前跟踪、技术支持、需…...
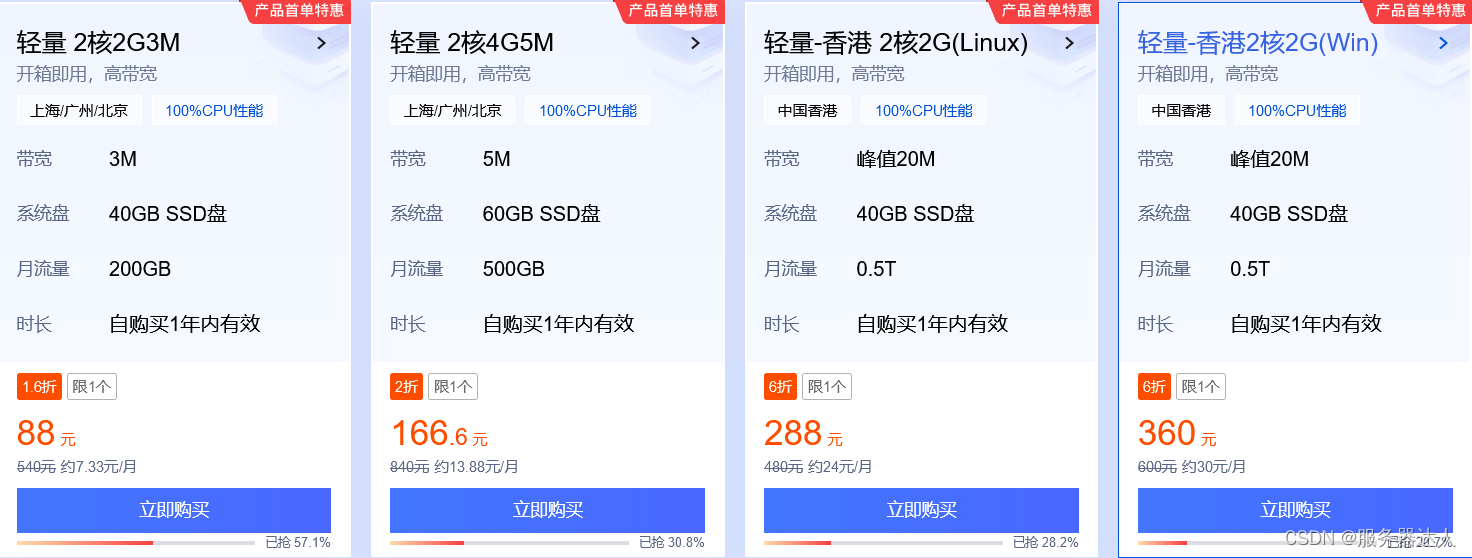
阿里云99元VS腾讯云88元,双11云服务器价格战,谁胜谁负?
在2023年的双十一优惠活动中,阿里云推出了一系列令人惊喜的优惠活动,其中包括99元一年的超值云服务器。本文将带您了解这些优惠活动的具体内容,以及与竞争对手腾讯云的价格对比,助您轻松选择最适合的云服务器。 99元一年服务器优…...

1.jvm基本知识
目录 概述jvm虚拟机三问jvm是什么?java 和 jvm 的关系 为什么学jvm怎么学习为什么jvm调优?什么时候jvm调优调优调什么 结束 概述 相关文章在此总结如下: 文章地址jvm类加载系统地址双亲委派模型与打破双亲委派地址运行时数据区地址运行时数据区-字符串…...

前端---掌握WebAPI:DOM
文章目录 什么是DOM?使用DOM获取元素事件操作元素获取、修改元素内容获取、修改元素属性获取、修改表单元素属性:input获取、修改样式属性直接修改样式:行内样式通过修改class属性来修改样式 新增节点删除节点 什么是DOM? DOM&am…...
)
最优化基础(一)
最优化基础(一)1 最优化问题的数学模型 通俗地说,所谓最优化问题,就是求一个多元函数在某个给定集合上的极值. 几乎所有类型的最优化问题都可以用下面的数学模型来描述: m i n f ( x ) s . t . x ∈ Ω min\ f({x})\\ s.t. \ {…...

基于JavaWeb+SpringBoot+Vue医疗器械商城微信小程序系统的设计和实现
基于JavaWebSpringBootVue医疗器械商城微信小程序系统的设计和实现 源码获取入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码获取入口 前言 摘 要 目前医疗器械行业作为医药行业的一个分支,发展十分迅速。…...

java程序中为什么经常使用tomcat
该疑问的产生场景: 原来接触的ssm项目需要在项目配置中设置tomcat,至于为什么要设置tomcat不清楚,只了解需要配置tomcat后项目才能启动。接触的springboot在项目配置中不需要配置tomcat,原因是springboot框架内置了tomcat…...

大带宽服务器需要选择哪些节点
选择大带宽服务器节点需要考虑以下几个因素: 地理位置:选择距离用户较近的节点,可以降低延迟,提高响应速度。 网络质量:大带宽服务器节点应该有良好的网络质量,稳定可靠,能够提供高速的网络传输…...
)
CSS 属性学习笔记(入门)
1. 选择器 CSS选择器用于选择要样式化的HTML元素。以下是一些常见的选择器: 元素选择器 p {color: blue; }描述: 选择所有 <p> 元素,并将文本颜色设置为蓝色。 类选择器 .highlight {background-color: yellow; }描述:…...

[Android]使用View Binding 替代findViewById
1.配置 build.gradle文件中添加配置,然后同步。 android {...buildFeatures {viewBinding true} } 2.用 View Binding 类来访问布局中的视图 在Activity代码的顶部导入生成的 View Binding 类: import com.example.yourapp.databinding.ActivityMai…...

Pytest UI自动化测试实战实例
环境准备 序号库/插件/工具安装命令1确保您已经安装了python3.x2配置python3pycharmselenium2开发环境3安装pytest库 pip install pytest 4安装pytest -html 报告插件pip install pytest-html5安装pypiwin32库(用来模拟按键)pip install pypiwin32 6安装openpyxl解析excel文…...

软件测试/测试开发丨接口自动化测试学习笔记,多环境自动切换
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/28026 多环境介绍 环境使用场景备注dev开发环境开发自测QA测试环境QA日常测试preprod预发布环境回归测试、产品验测试prod线上环境用户使用的环境 通过环…...

Spring-IoC与DI入门案例
IoC入门案例 IoC入门案例思路分析 管理什么?(Service与Dao)如何将被管理的对象告知IoC容器?(配置)被管理的对象交给IoC容器,如何获取到IoC容器?(接口)IoC容…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
