Java编程陷阱(三)
陷阱11:不要使用StringBuffer类来拼接字符串
StringBuffer是Java中的一个类,它可以表示一个可变的字符串,也就是可以对字符串进行修改和追加的操作,比如使用append或insert方法来拼接字符串。- 有时候,我们需要使用
StringBuffer类来拼接字符串,比如在循环中动态地构建一个字符串,就需要使用StringBuffer类的方法来创建和操作字符串。 - 但是,如果我们使用
StringBuffer类来拼接字符串,就可能导致一些意想不到的结果,甚至引发错误。
错误的代码
// 使用StringBuffer类来创建一个字符串缓冲对象,初始为空
StringBuffer sb = new StringBuffer();
// 使用for循环来拼接字符串,每次追加一个字母
for (char c = 'A'; c <= 'Z'; c++) {// 使用append方法向字符串缓冲对象追加一个字母sb.append(c);
}
// 打印字符串缓冲对象的内容,期望得到字母表
System.out.println(sb); // ABCDEFGHIJKLMNOPQRSTUVWXYZ
// 使用StringBuffer类的reverse方法来反转字符串缓冲对象的内容
sb.reverse();
// 打印字符串缓冲对象的内容,期望得到反转后的字母表
System.out.println(sb); // ZYXWVUTSRQPONMLKJIHGFEDCBA
为什么会出错呢?
- 因为使
相关文章:
)
Java编程陷阱(三)
陷阱11:不要使用StringBuffer类来拼接字符串 StringBuffer是Java中的一个类,它可以表示一个可变的字符串,也就是可以对字符串进行修改和追加的操作,比如使用append或insert方法来拼接字符串。有时候,我们需要使用StringBuffer类来拼接字符串,比如在循环中动态地构建一个字…...

数据仓库相关
在阿里巴巴的数据体系中,我们建议将数据仓库分为三层,自下而上为:数据引入层(ODS,Operation Data Store)、数据公共层(CDM,Common Data Model)和数据应用层(…...
)
SpringBoot学习笔记-创建个人中心页面(下)
笔记内容转载自 AcWing 的 SpringBoot 框架课讲义,课程链接:AcWing SpringBoot 框架课。 CONTENTS 1. 实现个人中心页面2. POJO时区修改3. 集成代码编辑器 本节实现个人中心的前端页面,用户能够查看自己的 Bot 信息,并能创建、修改…...

电子秤方案:做一个宠物勺方案设计
养宠物是一件费心劳力的事情,但同时也是能够给你带来快乐和幸福感的事情。就是有时候会怕宠物毫无征兆地生病令人措手不及,所以电子秤方案设计鼎盛合科技分享一个小方案,能够及时了解到宠物的身体状况问题。 蓝牙宠物勺是一种具有记录和称重…...
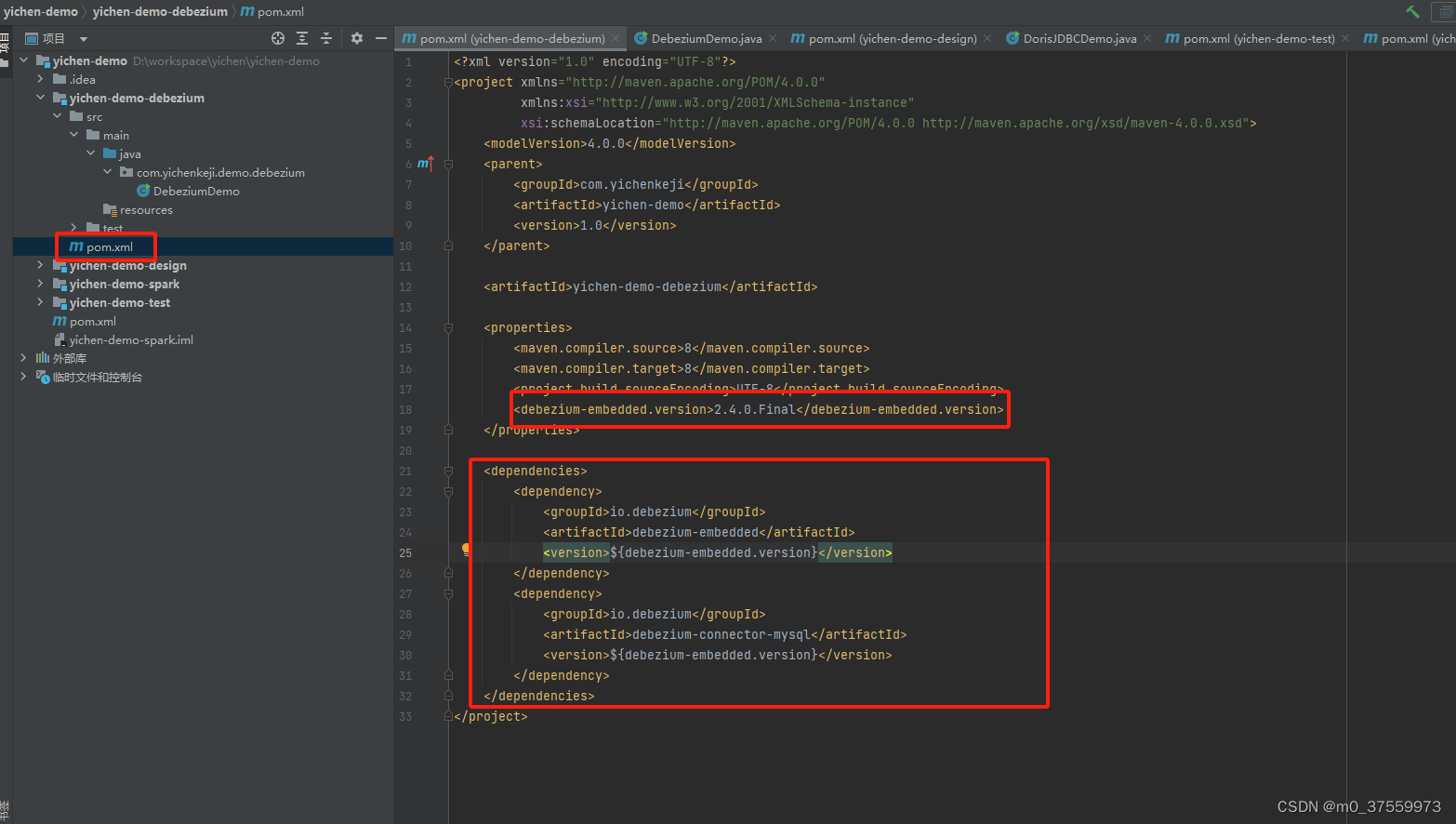
Debezium-Embedded 实时监控MySQL数据变更
1.Debezium-Embedded 简介 Debezium连接器的操作通常是将它们部署到Kafka Connect服务,并配置一个或多个连接器来监控上游数据库,并为它们在上游数据库中看到的所有更改生成数据更改事件。这些数据更改事件被写入Kafka,在那里它们可以被许多不…...
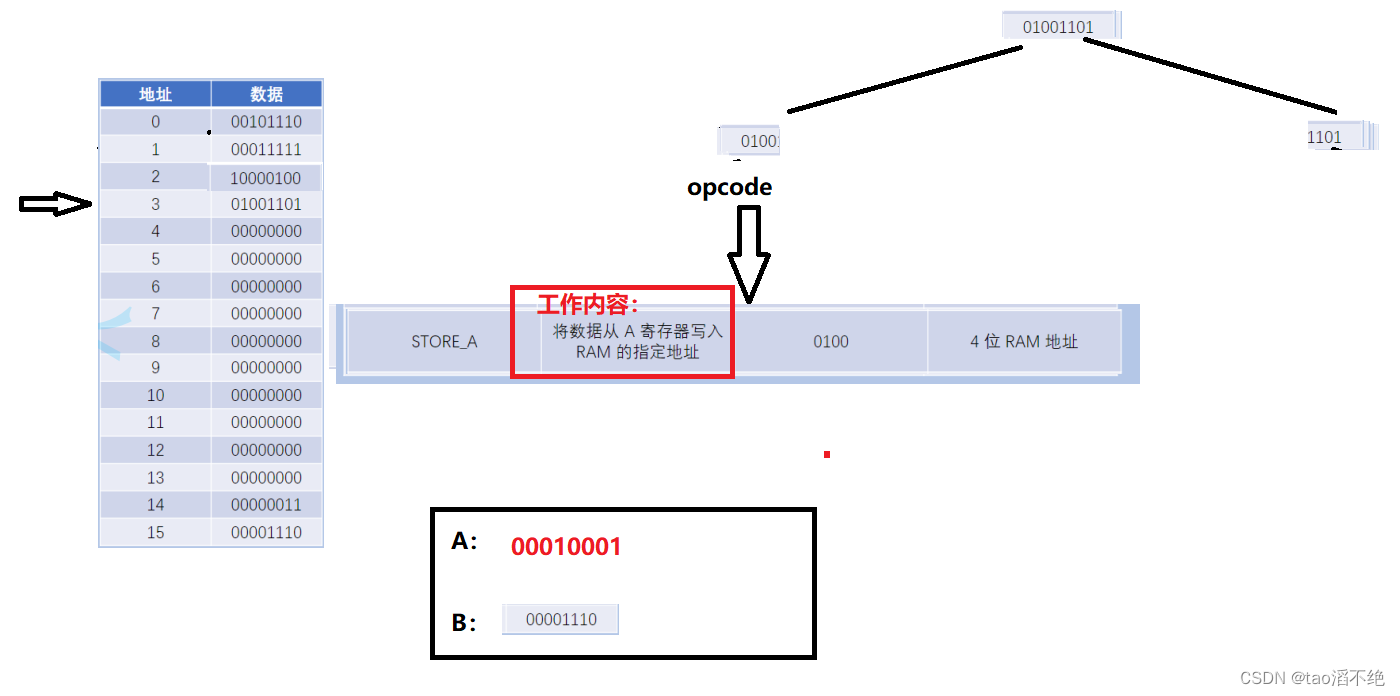
计算机是如何工作的(简单介绍)
目录 一、冯诺依曼体系 二、CPU基本流程工作 逻辑⻔ 电⼦开关——机械继电器(Mechanical Relay) ⻔电路(Gate Circuit) 算术逻辑单元 ALU(Arithmetic & Logic Unit) 算术单元(ArithmeticUnit) 逻辑单元(Logic Unit) ALU 符号 寄存器(Regis…...
JSP基本表单和Request对象使用例子
表单的jsp; <%page contentType"text/html;charsetgbk" pageEncoding"UTF-8"%> <!DOCTYPE html> <html><head><meta http-equiv"Content-Type" content"text/html; charsetUTF-8"><titl…...
【Redux】Redux 基本使用
1. Redux 快速上手 Redux 是 React 最常用的集中状态管理工具,类似于Vue中的Pinia(Vuex),可以独立于框架运行。 <button id"decrement">-</button> <span id"count">0</span> <…...
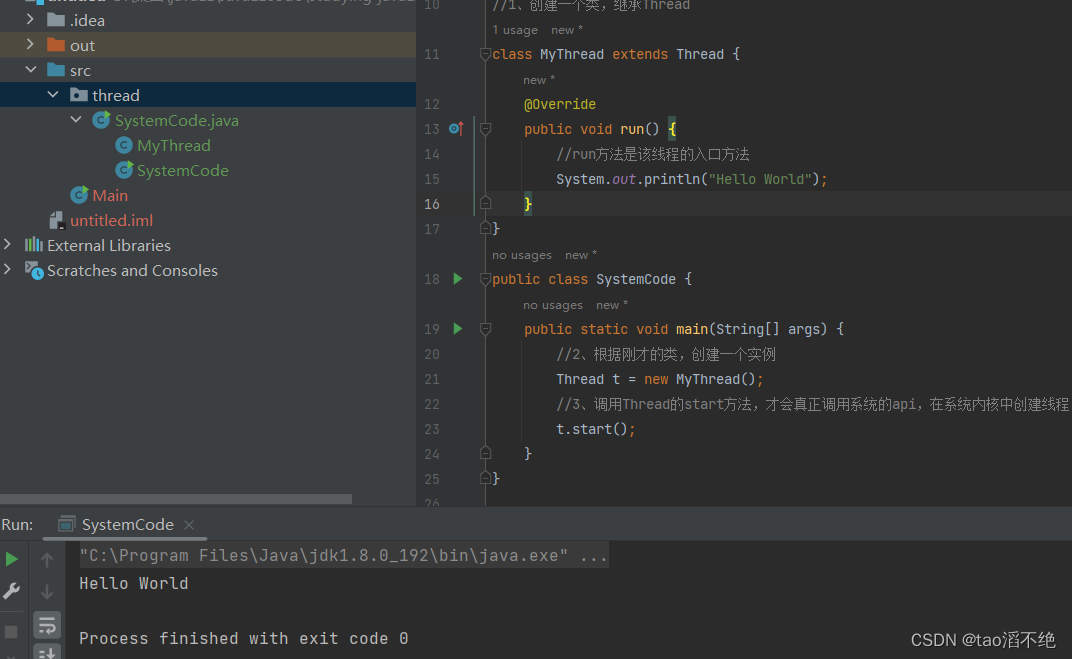
多线程Thread(初阶一:认识线程)
目录 一、引用线程的原因 二、线程的概念 三、进程和线程的区别 四、多线程编程 一、引用线程的原因 多任务操作系统,希望系统能同时运行多个任务。所以会涉及到进程,需要对进程进行管理、调度等。 而单任务操作系统,就完全不涉及到进程…...
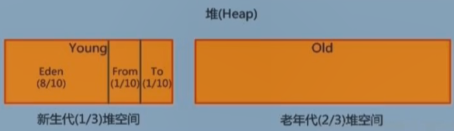
系列五、GC垃圾回收【四大垃圾算法-复制算法】
一、堆的内存组成 二、复制算法 2.1、发生位置 复制算法主要发生在新生代,发生在新生代的垃圾回收也被叫做Minor GC。 2.2、 Minor GC的过程 复制>清空》交换 1、eden、from区中的对象复制到to区,年龄1 首先,当eden区满的时候会触发第一…...
LeetCode(24)文本左右对齐【数组/字符串】【困难】
目录 1.题目2.答案3.提交结果截图 链接: 文本左右对齐 1.题目 给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。 你应该使用 “贪心算法” 来放置给定的单…...

Spring-Spring之事务底层源码解析
EnableTransactionManagement工作原理 开启Spring事务本质上就是增加了一个Advisor,但我们使用EnableTransactionManagement注解来开启Spring事务是,该注解代理的功能就是向Spring容器中添加了两个Bean: AutoProxyRegistrarProxyTransactio…...
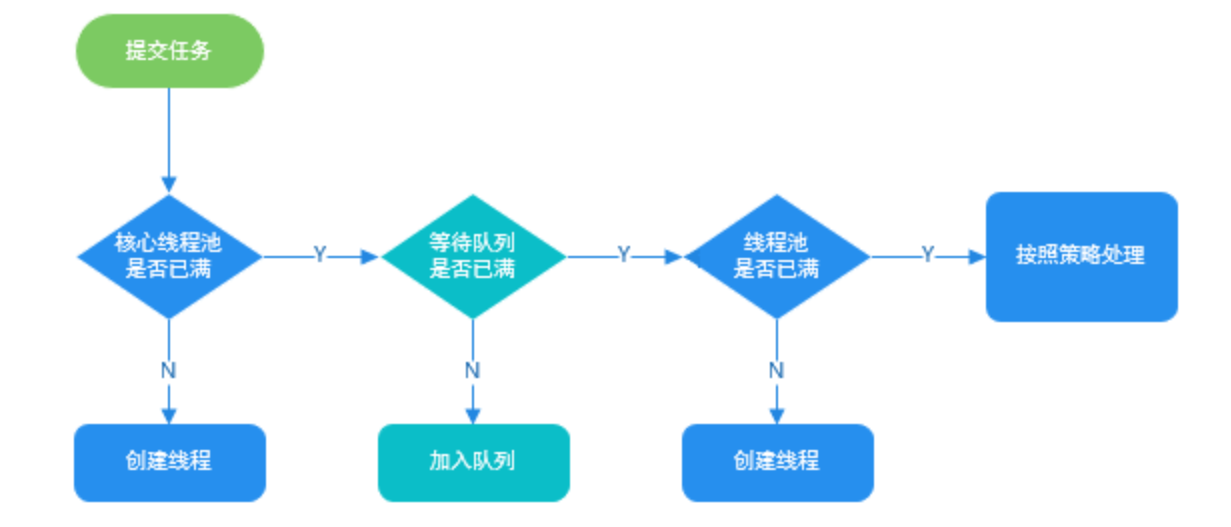
后端面经学习自测(三)
文章目录 1、ArrayList和Linkedlist区别?2、ArrayList扩容机制?3、ArrayList和Linkedlist分别能做什么场景?4、事务特性?MySQL事务Redis事务Spring事务5、在Spring中事务失效的场景?6、Java泛型?7、泛型擦除…...

力扣labuladong——一刷day40
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣341. 扁平化嵌套列表迭代器 前言 N叉树的结构,构造迭代器 一、力扣341. 扁平化嵌套列表迭代器 /*** // This is the interface that allo…...
在VS Code中使用VIM
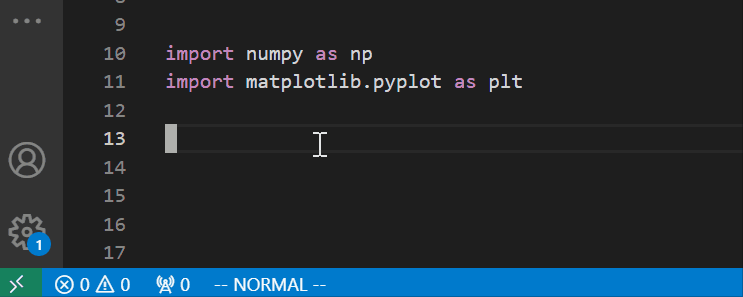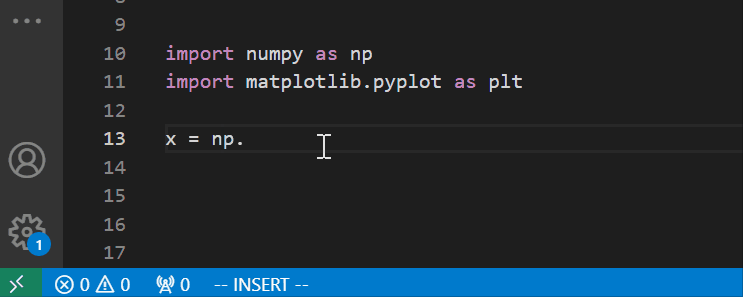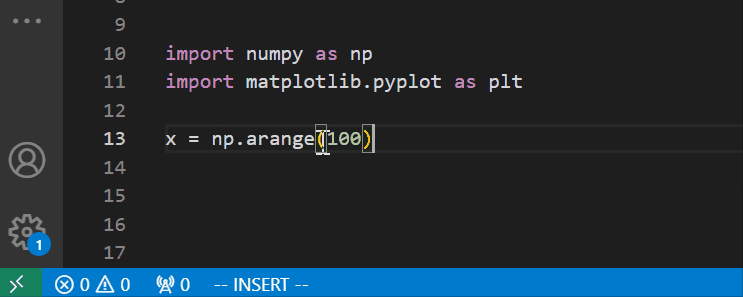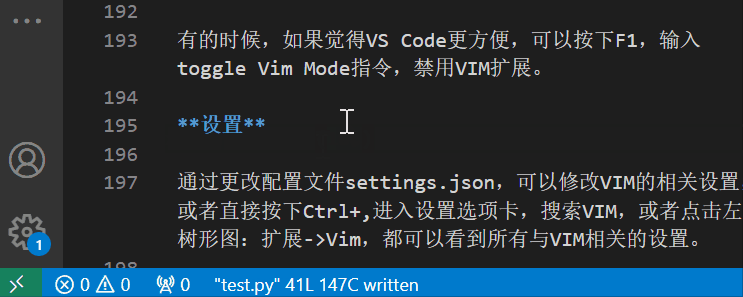
文章目录 安装和基本使用设置 安装和基本使用 VIM是VS Code的强大对手,其简化版本VI是Linux内置的文本编辑器,堪称VS Code问世之前最流行的编辑器,也是VS Code问世之后,我仍在使用的编辑器。 对VIM无法割舍的原因有二࿰…...

注解【元数据,自定义注解等概念详解】(超简单的好吧)
注解的理解与使用 注解的释义元数据的含义基础阶段常见的注解注解的作用(包括但不限于)教你读懂注解内部代码内容五种元注解尝试解读简单注解我当时的疑惑点 自定义注解自定义注解举例 注解的原理总结 注解的释义 我们都知道注释是拿来给程序员看的&…...

vue-pdf在vue框架中的使用
在components目录下新建PdfViewer/index.vue vue-pdf版本为4.3.0 <template><div :id"containerId" v-if"hasProps" class"container"><div class"right-btn"><div class"pageNum"><input v-m…...

Wordpress页面生成器:Elementor 插件制作网站页面教程(图文完整)
本文来教大家怎么使用Wordpress Elementor页面编辑器插件来自由创建我们的网页内容。很多同学在面对建站的时候,一开始都是热血沸腾信心满满的,等到实际上手的时候就会发现有很多问题都是无法解决的,希望本篇Elementor插件使用指南能够帮助到你。 Wordpress Elementor页面编…...
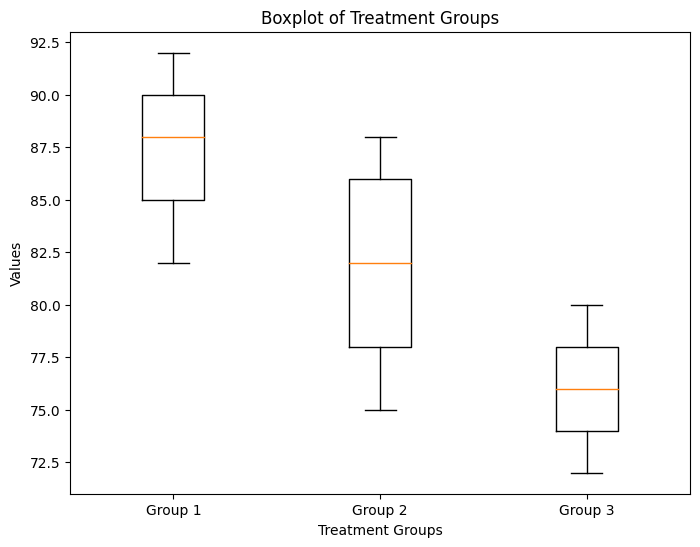
完全随机设计的方差分析
一、说明 实验设计在科学研究中发挥着至关重要的作用,使研究人员能够从数据中得出有意义的结论。一种常见的实验设计是完全随机设计(CRD),其特征是将实验单元随机分配到治疗组。CRD 的方差分析 (ANOVA) 是一种统计技术,…...

035、目标检测-物体和数据集
之——物体检测和数据集 目录 之——物体检测和数据集 杂谈 正文 1.目标检测 2.目标检测数据集 3.目标检测和边界框 4.目标检测数据集示例 杂谈 目标检测是计算机视觉中应用最为广泛的,之前所研究的图片分类等都需要基于目标检测完成。 在图像分类任务中&am…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
