完全随机设计的方差分析
一、说明
实验设计在科学研究中发挥着至关重要的作用,使研究人员能够从数据中得出有意义的结论。一种常见的实验设计是完全随机设计(CRD),其特征是将实验单元随机分配到治疗组。CRD 的方差分析 (ANOVA) 是一种统计技术,用于确定治疗组之间是否存在统计显着差异。在本文中,我们将探讨 CRD 方差分析的基本原理、其假设及其在现实世界研究中的应用。

完全随机设计的方差分析:科学与随机性相遇,揭示显着性模式。
二、完全随机设计:简要概述
完全随机设计是一种基本的实验设计,当研究人员有兴趣比较多个治疗或组时特别有用。在 CRD 中,实验单位被随机分配到不同的治疗组。这种随机化有助于消除偏差,并确保估计的治疗效果是无偏差的,并且可以推广到抽取样本的人群。
CRD 的关键组件包括:
- 治疗组:这些是正在测试的自变量的各个水平。每个组接受不同的治疗或条件。
- 随机分配:将实验单元随机分配到治疗组的过程,以确保每个单元有平等的机会被分配到任何组。
- 响应变量:为评估治疗效果而测量或观察的变量。
三、CRD 的方差分析
方差分析是一种统计方法,用于确定两个或多个组的平均值是否彼此显着不同。CRD 的方差分析专门解决了治疗组平均值之间是否存在显着差异的问题。该技术将数据的总变异分为两个部分:治疗组之间的变异和治疗组内的变异。
在数学上,CRD 的 ANOVA 模型可以表示为:
Yij = μ + τi + εij
其中:
- Yij 代表第 i 个治疗组中第 j 个个体的观察结果。
- μ 是总体平均值。
- τi 是第 i 个治疗组的效果。
- εij 是与第 i 个治疗组中第 j 个观察值相关的随机误差。
四、CRD 方差分析的假设
为了确保方差分析结果的有效性,必须满足几个假设:
- 独立性:治疗组内和治疗组之间的观察必须彼此独立。
- 正态性:残差的分布(观测值与预测值之间的差异)应近似正态分布。
- 方差同质性:所有治疗组的残差方差应保持恒定,这意味着每组内的变异性应大致相等。
- 随机分配:实验单位必须被随机分配到治疗组。
五、方差分析在 CRD 中的应用
CRD 方差分析广泛应用于各个科学研究领域,包括生物学、心理学、农业和制造业。让我们考虑一些实际的例子:
- 农业:研究人员可以使用 CRD 方差分析来比较不同肥料对作物产量的影响,以确定哪种肥料可使作物产量最高。
- 医学:临床试验经常使用 CRD 方差分析来评估不同药物治疗对特定病症的有效性。
- 心理学:心理学家可以采用 CRD 方差分析来研究各种疗法对患者心理健康结果的影响。
- 制造:质量控制工程师可以使用 CRD ANOVA 来评估不同制造工艺对产品质量的影响。
六、代码
下面是一个完整的 Python 代码示例,用于使用数据集执行完全随机设计 (CRD) 的方差分析 (ANOVA) 并生成相关图。为此,我们将使用scipy和库。matplotlib
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt# Sample dataset for three treatment groups (you can replace this with your own data)
data = {'Group1': [82, 85, 88, 90, 92],'Group2': [75, 78, 82, 86, 88],'Group3': [72, 74, 76, 78, 80]
}# Create a pandas DataFrame from the dataset
df = pd.DataFrame(data)# Perform one-way ANOVA
f_statistic, p_value = stats.f_oneway(df['Group1'], df['Group2'], df['Group3'])# Output ANOVA results
print("F-statistic:", f_statistic)
print("p-value:", p_value)# Determine whether the differences are statistically significant
alpha = 0.05
if p_value < alpha:print("The differences are statistically significant (reject the null hypothesis).")
else:print("The differences are not statistically significant (fail to reject the null hypothesis).")# Plot the data
plt.figure(figsize=(8, 6))
plt.boxplot([df['Group1'], df['Group2'], df['Group3']], labels=['Group 1', 'Group 2', 'Group 3'])
plt.title('Boxplot of Treatment Groups')
plt.xlabel('Treatment Groups')
plt.ylabel('Values')
plt.show()在此代码中,我们首先定义一个包含三个治疗组(Group1、Group2 和 Group3)的样本数据集。您可以将此数据替换为您自己的数据集。然后我们根据这个数据集创建一个 pandas DataFrame。
F-statistic: 8.861818181818181
p-value: 0.004329879787661512
The differences are statistically significant (reject the null hypothesis). 该代码继续执行单向方差分析,用于scipy.stats.f_oneway获取 F 统计量和 p 值。根据 p 值,它确定治疗组之间的差异在指定的显着性水平 (alpha) 下是否具有统计显着性。
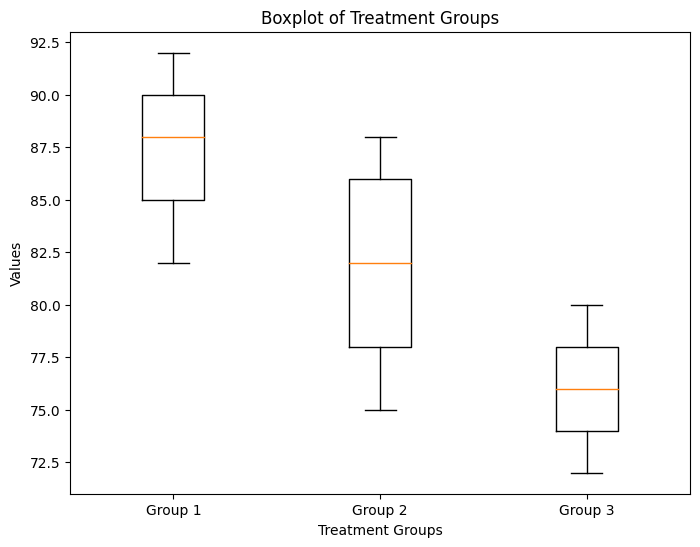
最后,代码生成一个箱线图来可视化每个治疗组中值的分布。
确保在您的 Python 环境中安装了pandas、scipy和库才能成功运行此代码。matplotlib
七、结论
完全随机设计的方差分析是一种强大的统计工具,使研究人员能够评估随机实验中治疗组之间差异的显着性。通过将数据的变化划分为组内和组间成分,方差分析可以帮助研究人员就不同治疗或条件的影响得出有意义的结论。必须确保满足独立性、正态性、方差同质性和随机分配的假设,以获得准确可靠的结果。CRD 方差分析仍然是科学研究的基石,有助于我们理解不同领域的各种现象。
相关文章:

完全随机设计的方差分析
一、说明 实验设计在科学研究中发挥着至关重要的作用,使研究人员能够从数据中得出有意义的结论。一种常见的实验设计是完全随机设计(CRD),其特征是将实验单元随机分配到治疗组。CRD 的方差分析 (ANOVA) 是一种统计技术,…...

035、目标检测-物体和数据集
之——物体检测和数据集 目录 之——物体检测和数据集 杂谈 正文 1.目标检测 2.目标检测数据集 3.目标检测和边界框 4.目标检测数据集示例 杂谈 目标检测是计算机视觉中应用最为广泛的,之前所研究的图片分类等都需要基于目标检测完成。 在图像分类任务中&am…...

【开源】基于Vue.js的社区买菜系统的设计和实现
项目编号: S 011 ,文末获取源码。 \color{red}{项目编号:S011,文末获取源码。} 项目编号:S011,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、系统设计2.1 功能模块设计2.1.1 数据中心模块2.1…...
【双指针】复写0
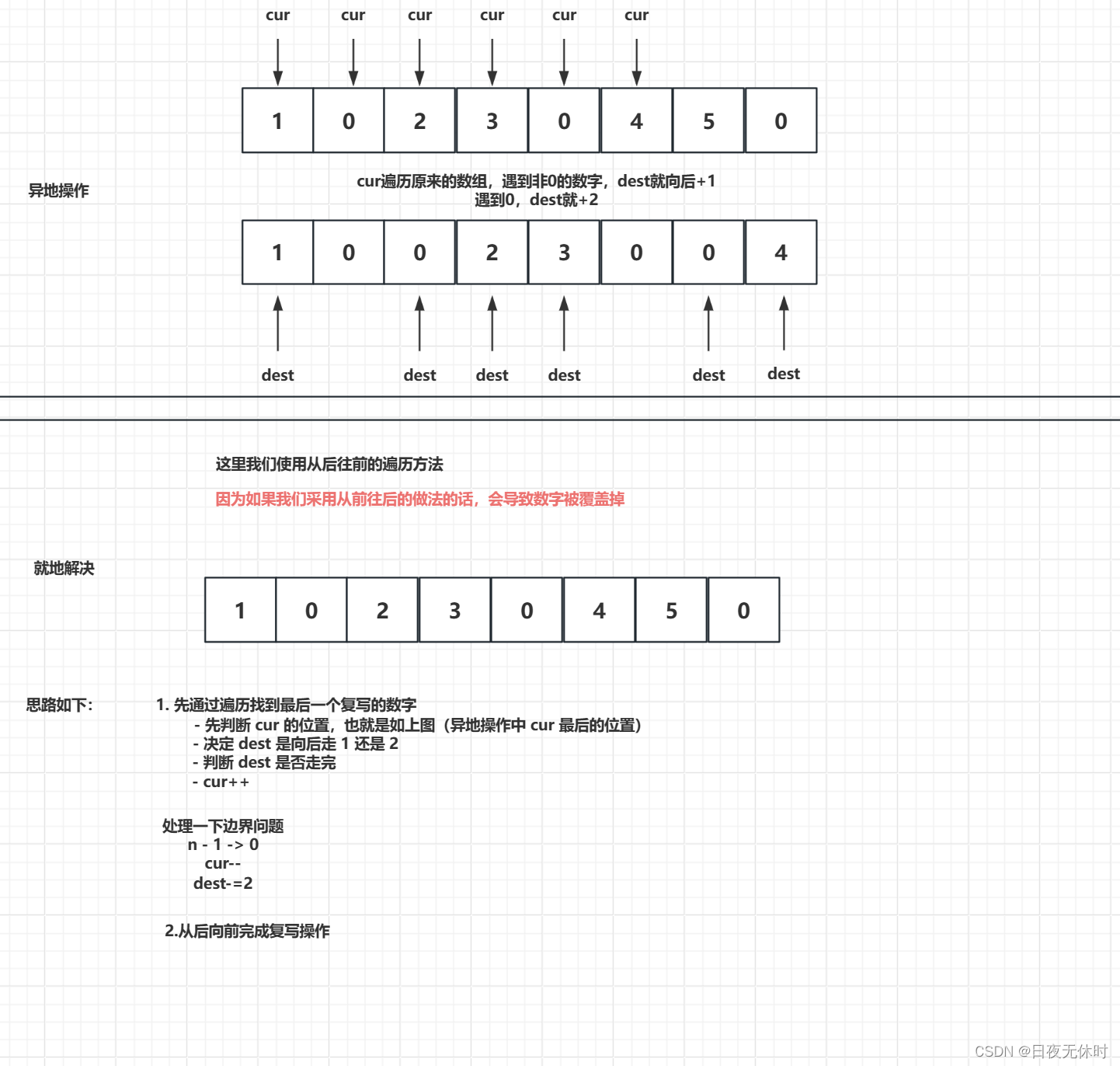
复写0 1089. 复写零 - 力扣(LeetCode) 给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。 注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上…...

记录一些涉及到界的题
文章目录 coppersmith的一些相关知识题1 [N1CTF 2023] e2Wrmup题2 [ACTF 2023] midRSA题3 [qsnctf 2023]浅记一下 coppersmith的一些相关知识 上界 X c e i l ( 1 2 ∗ N β 2 d − ϵ ) X ceil(\frac{1}{2} * N^{\frac{\beta^2}{d} - \epsilon}) Xceil(21∗Ndβ2−ϵ) …...

Linux秋招面试题
自己在秋招过程中遇到的Linux相关的面试题 linux查找含有“xxxx”的文件名 将/path/to/search替换为要搜索的目录路径,xxxx表示要匹配的文件名模式,其中xxxx是你要查找的字符串。这个命令将会在指定路径下递归地查找所有文件名中包含给定字符串的文件 …...

OPPO发布AndesGPT大模型;Emu Video和Emu Edit的新突破
🦉 AI新闻 🚀 OPPO发布全新ColorOS 14及自主训练的AndesGPT大模型 摘要:OPPO在2023 OPPO开发者大会上发布了全新的ColorOS 14,并正式推出了自主训练的安第斯大模型(AndesGPT)。AndesGPT拥有对话增强、个人…...

2311rust,到46版本更新
1.43.0稳定版 项(item)片段 在宏中,可用项片段把项插值到特征,实现和extern块的块体中.如: macro_rules! mac_trait {($i:item) > {trait T { $i }} } mac_trait! {fn foo() {} }这生成: trait T {fn foo() {} }围绕原语的推导类型 改进了围绕原语,引用和二进制操作的推…...

Rust根据条件删除相邻元素:dedup
文章目录 示例dedup_bydedup_by_key Rust系列:初步⚙所有权⚙结构体和枚举类⚙函数进阶⚙泛型和特征⚙并发和线程通信 示例 Rust中的动态数组Vec提供了dedup函数,用于删除相邻重复元素。此外,还提供了dedup_by和dedup_by_key,可…...
2023年(第六届)电力机器人应用与创新发展论坛-核心PPT资料下载
一、峰会简介 大会以“聚焦电力机器人创新、助力行业数字化转型、促进产业链协同发展”为主题,展示电力机器人产业全景创新技术,探讨数字化战略下电力机器人应用前景和发展趋势。为加快推进电力机器人应用拓新,助力电网数字化转型升级&#…...
Android BitmapFactory.decodeResource读取原始图片装载成原始宽高Bitmap,Kotlin
Android BitmapFactory.decodeResource读取原始图片装载成原始宽高Bitmap,Kotlin fun getOriginalBitmap(resId: Int): Bitmap {val options BitmapFactory.Options()options.inJustDecodeBounds true //只解析原始图片的宽高,不decode原始文件装载到内…...
阿里云服务器 手动搭建WordPress(CentOS 8)
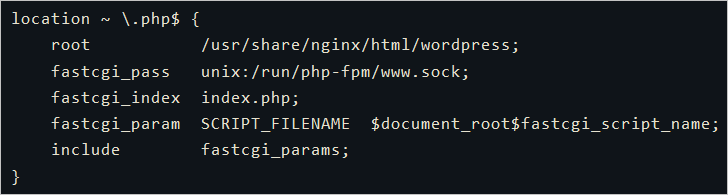
前提条件 已创建Linux操作系统的ECS实例,并且手动部署LNMP环境,具体操作,请参见手动部署LNMP环境(CentOS 8)。本教程使用的相关资源版本如下。 实例规格:ecs.c6.large 操作系统:公共镜像CentO…...

竞赛 题目:基于深度学习的中文对话问答机器人
文章目录 0 简介1 项目架构2 项目的主要过程2.1 数据清洗、预处理2.2 分桶2.3 训练 3 项目的整体结构4 重要的API4.1 LSTM cells部分:4.2 损失函数:4.3 搭建seq2seq框架:4.4 测试部分:4.5 评价NLP测试效果:4.6 梯度截断…...

CCF ChinaSoft 2023 论坛巡礼|软件测试产教研融合论坛
2023年CCF中国软件大会(CCF ChinaSoft 2023)由CCF主办,CCF系统软件专委会、形式化方法专委会、软件工程专委会以及复旦大学联合承办,将于2023年12月1-3日在上海国际会议中心举行。 本次大会主题是“智能化软件创新推动数字经济与社…...
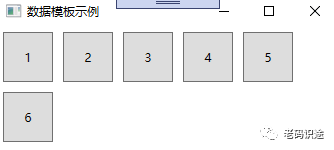
浅谈WPF之控件模板和数据模板
WPF不仅支持传统的Windows Forms编程的用户界面和用户体验设计,同时还推出了以模板为核心的新一代设计理念。在WPF中,通过引入模板,将数据和算法的“内容”和“形式”进行解耦。模板主要分为两大类:数据模板【Data Template】和控…...
微信小程序会议OA首页-开发说明创建项目关于flex布局关于尺寸单位(rpx)关于WXS轮播图会议信息
目录 1. 创建项目 2. 关于flex布局 3. 关于尺寸单位(rpx) 4. 关于WXS 4. 轮播图 5. 会议信息 1. 创建项目 基于微信原生开发工具,稳定版 Stable Build (1.06.22010310) 创建项目前,请确定有小程序测试账号 使用向导创建一个…...
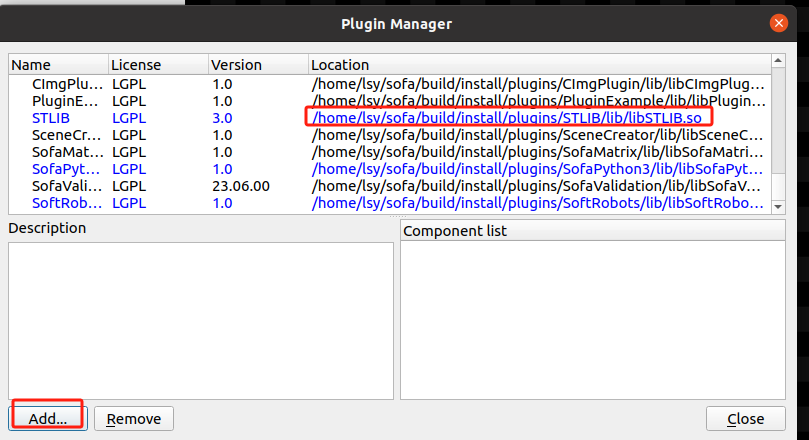
Linux上编译和安装SOFA23.06
前言 你可以直接使用编译安装好的SOFA版本Installing from all-included binaries (v23.06.00): 如果你想自己编译,可以看我下面写的内容,不过绝大多数是从官网来的,如果和官网有出入,建议还是以官网为准。 在Linux下…...

定时任务 Spring Task
一、介绍 Spring Task 是Spring框架提供的任务调度工具,可以按照约定的时间自动执行某个代码逻辑。 定位: 定时任务框架 作用: 定时自动执行某段Java代码 二、cron 表达式 cron表达式在线生成器:https://cron.qqe2.com/ 1、说明…...

golang 上传图片 --chatGPT
问:makeImgUpload(path string) 实现发送发送图片, 发送类型为 multipart/form-data gpt: 下面是一个简单的 makeImgUpload 函数的实现,用于发送图片并以 multipart/form-data 格式进行上传。请注意,此代码假设图片文件路径是正确…...
Android Studio 写一个Java调用c++ 的demo
前提条件: 本地已经配置好了ndk环境,如果没有配置好,建议参考macos 配置ndk环境-CSDN博客 这篇链接。 新建一个Empty Project 比如我这里的Project的名字是HelloJNI,包名是com.example.hellojni 然后在src目录下,右键选择Add C …...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
