【力扣面试经典150题】(链表)K 个一组翻转链表
题目描述
力扣原文链接
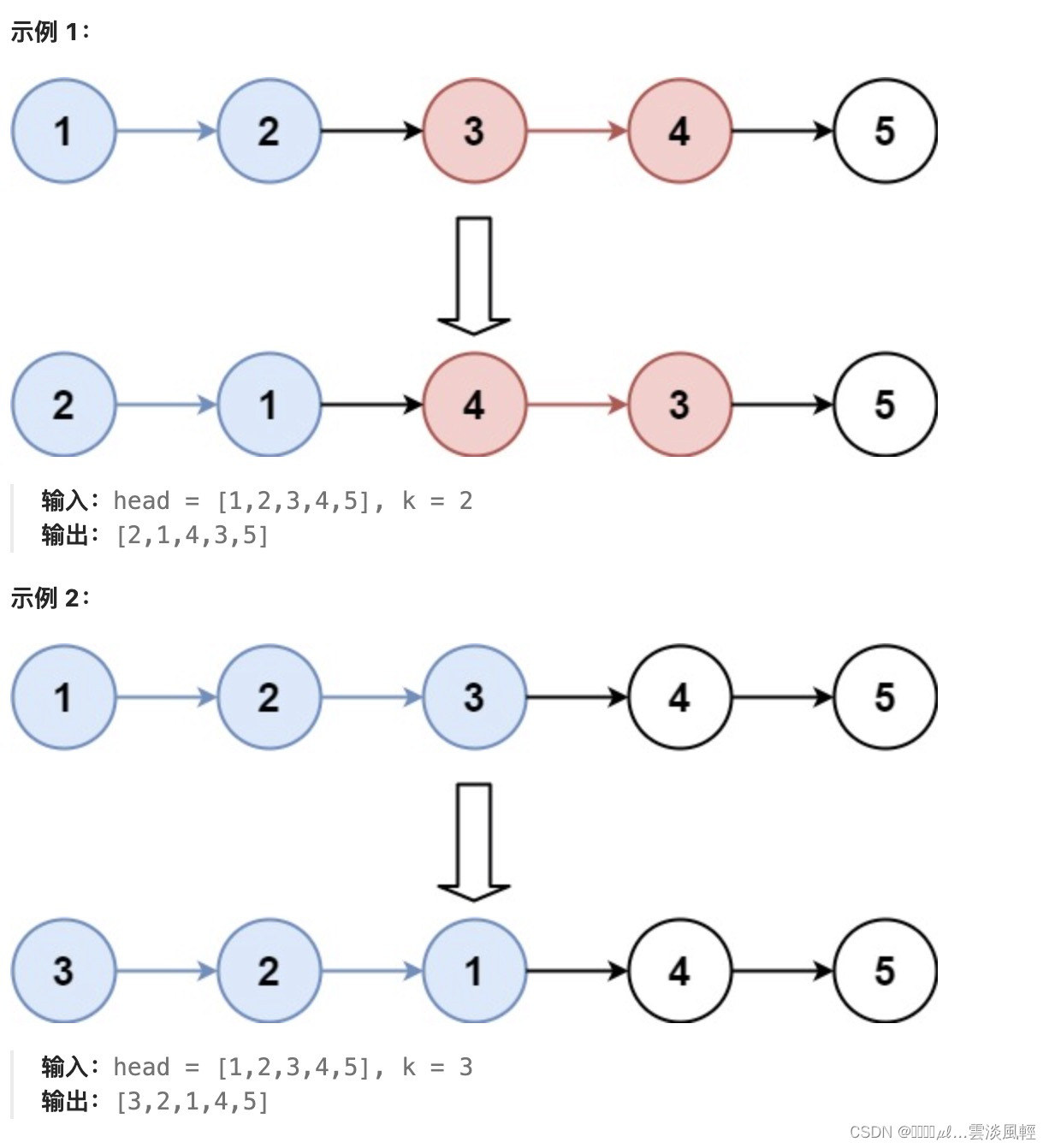
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
提示:
- 链表中的节点数目为 n
- 1 <= k <= n <= 5000
- 0 <= Node.val <= 1000
进阶:
你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗?
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode reverseKGroup(ListNode head, int k) {// here is your code }
}
解题过程
解题思路
拿到的题目以后,应该尽量根据已知条件、函数的入参和返回值抓住变与不变的量、考虑边界条件、加之常用算法手段,如递归、迭代、双指针、回溯、分治、动态规划等等,从而创造一条完整链路,再考虑时间复杂度和空间复杂度的限制,问题得解。
回到本题,函数入参是一个自定义的ListNode,以及指定的(小于ListNode长度的)正整数用以翻转子链表,最终将新链表返回。所以核心问题有两点:
- 函数入参指定的链表是否存在一个或者多个长度为K的子链表?
- 如果存在长度为K的子链表,如何实现这个不断重复的翻转子链表的工作?
接下来把代码要实现的逻辑完整地梳理一遍:
针对以上的两个问题,我们最少要进行一次O(n) 时间复杂度的链表遍历,来确定是否存在合理值K。如果不存在直接返回原链表,因为无需翻转。这是最简单的情况。如果存在合理值K,那么怎么在O(1)空间复杂度的情况下保证子链表的翻转?以及翻转后与旧链表首尾节点的组装?
用一个简单实例说明:
假设链表为 1 -> 2 -> 3 ,K = 2,那么自然会脱口而出,2 -> 1 -> 3,这样看起来是不是很简单呢?
实际上处理过程同上面分析的一样,先判断是否含有K长度子链表,链表长度为3,K为2,当然符合条件,再把K长度子链表 1 -> 2 翻转成 2 -> 1,问题得以解决。
增加虚拟节点
通常地,在解决链表相关问题的时候,习惯性地在给定的链表头加一个节点,由于与题目无关,是我们虚构用来方便计算处理边界条件的,则把它称之为“虚拟节点”。⚠️注意,后面涉及链表相关的问题会常用到虚拟节点。
为了便于理解,现在以链表 1 -> 2 ->3 为例,画图说明:

这里我们将原来 链表 1- >2- >3 加上了一个虚拟节点,变成了 链表 -1 -> 1 -> 2 -> 3
至于为什么要加这个虚拟节点,下文在遍历链表的时候大有用处,我们会详细的说,现在只需要知道虚拟节点这个概念即可。
判断是否存在长度为K的子链表
回到实际问题,仍以链表 1 -> 2 ->3 为例,下图所示,每一个节点都有两个属性
- val 当前节点值
- next 下个节点
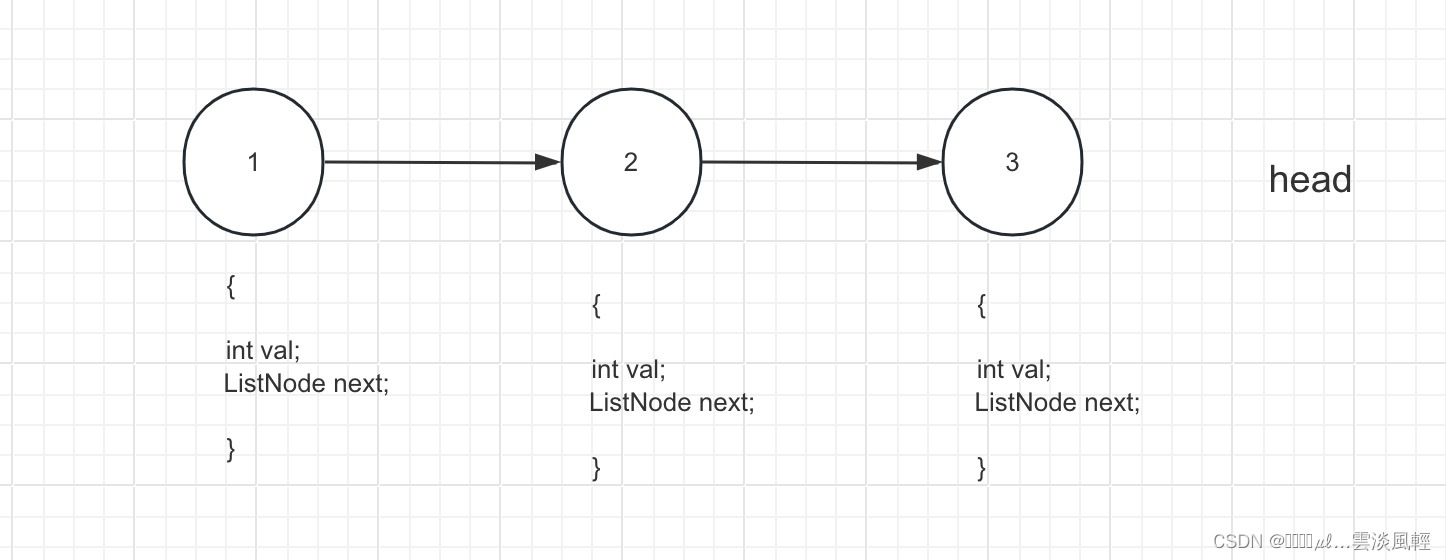 上图标注的整个链表,下文统一用head表示,head是从题目中函数入参拿到的哦
上图标注的整个链表,下文统一用head表示,head是从题目中函数入参拿到的哦
public ListNode reverseKGroup(ListNode head, int k)
首先我们在链表头部加上一个虚拟节点,并声明两个指针 prev 和 last 用来限定K长度子链表的边界。
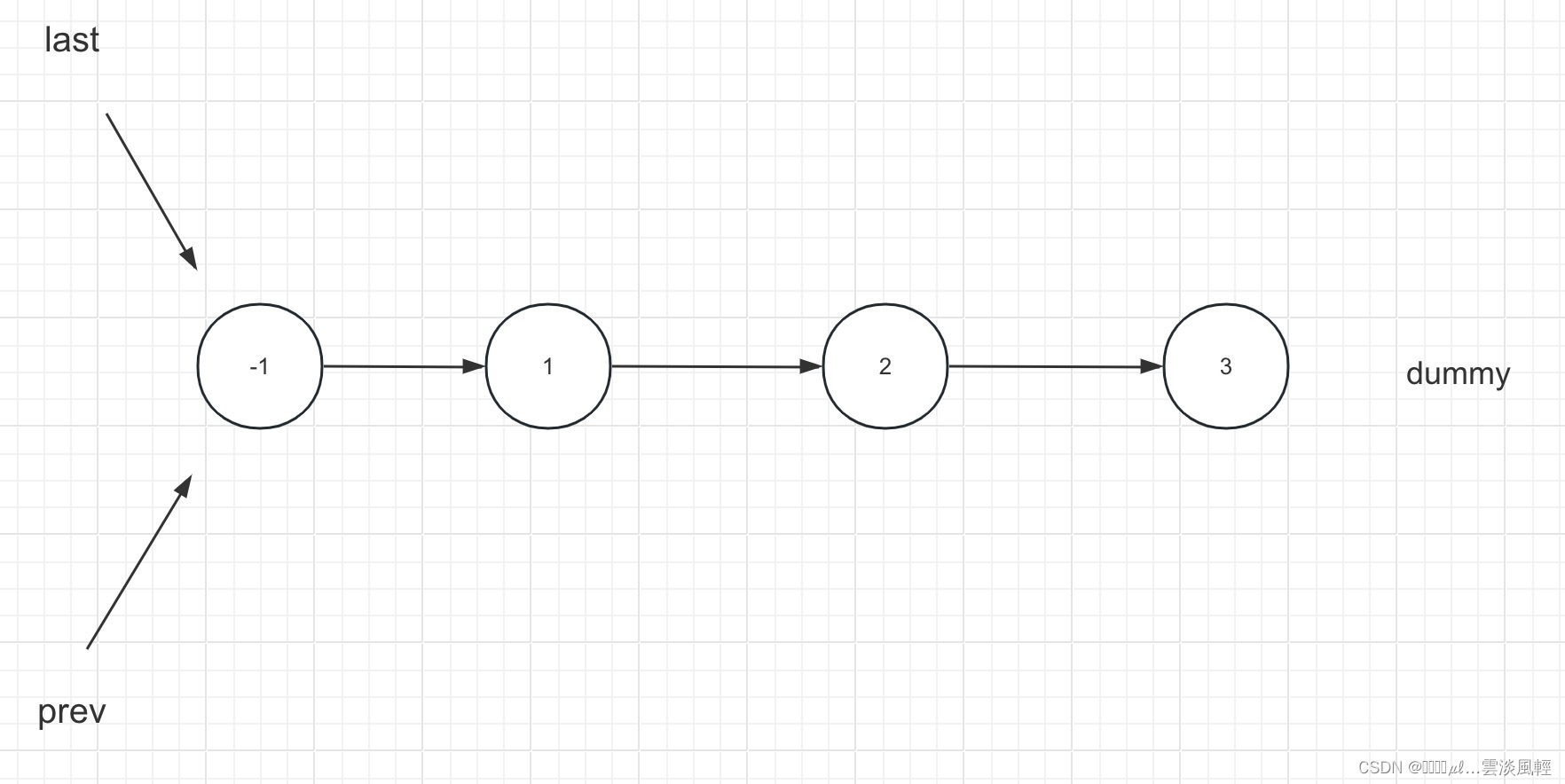
因为我们在入参的head上加了头部的虚拟节点,又加了两个指针,因此我们重新定义个新的dummy链表。
新的dummy链表 -1 -> 1 -> 2 ->3 ,并附加了两个指针 last 和 prev。
//模拟代码
//声明新的dummy链表,比之前的head链表多加了一个虚拟节点,值为-1,指向head
ListNode dummy = new ListNode(-1, head);
//在dummy链表上声明last指针,注意这里没有开辟新的空间
ListNode prev = dummy;
//注意,以上两行代码可以简写,与操作8大基本类型数据的声明是一样的道理,刚接触链表的同学可能看着有点懵,需要细心体会
ListNode dummy = new ListNode(-1, head), prev = dummy;
//在dummy链表上声明prev指针,注意这里没有开辟新的空间
ListNode last = prev;
现在通过移动last指针,移动的长度就是K,所以会有这样的写法:
//模拟代码
for(int i = 0;i < k;i++){//循环K次,每次移动last指针到下一个节点,因为是从虚拟节点开始移动,所以第一次移动后last一定指向dummy的第一个节点。last = last.next;//移动完要判断下一个节点是否为null,如果为null说明K循环未结束,而当前节点是末尾节点了,说明不足K个节点。直接返回dummy.next即可。if (last == null) {return dummy.next;}
}
通过K次循环last指针,判断dummy链表是否存在合理值K,直至last 为null

翻转长度为K的子链表
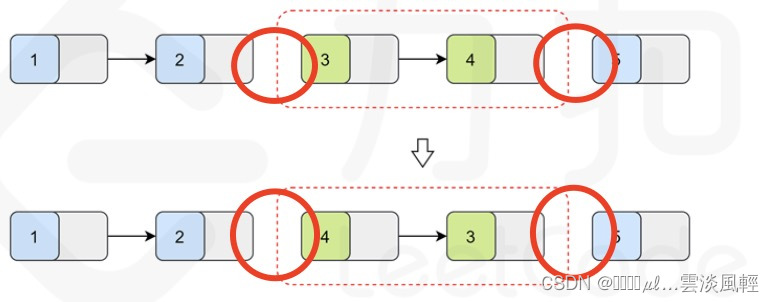
接着上面的实例,我们假设K=2,那么dummy链表的第一次K循环结束应该是这样的:
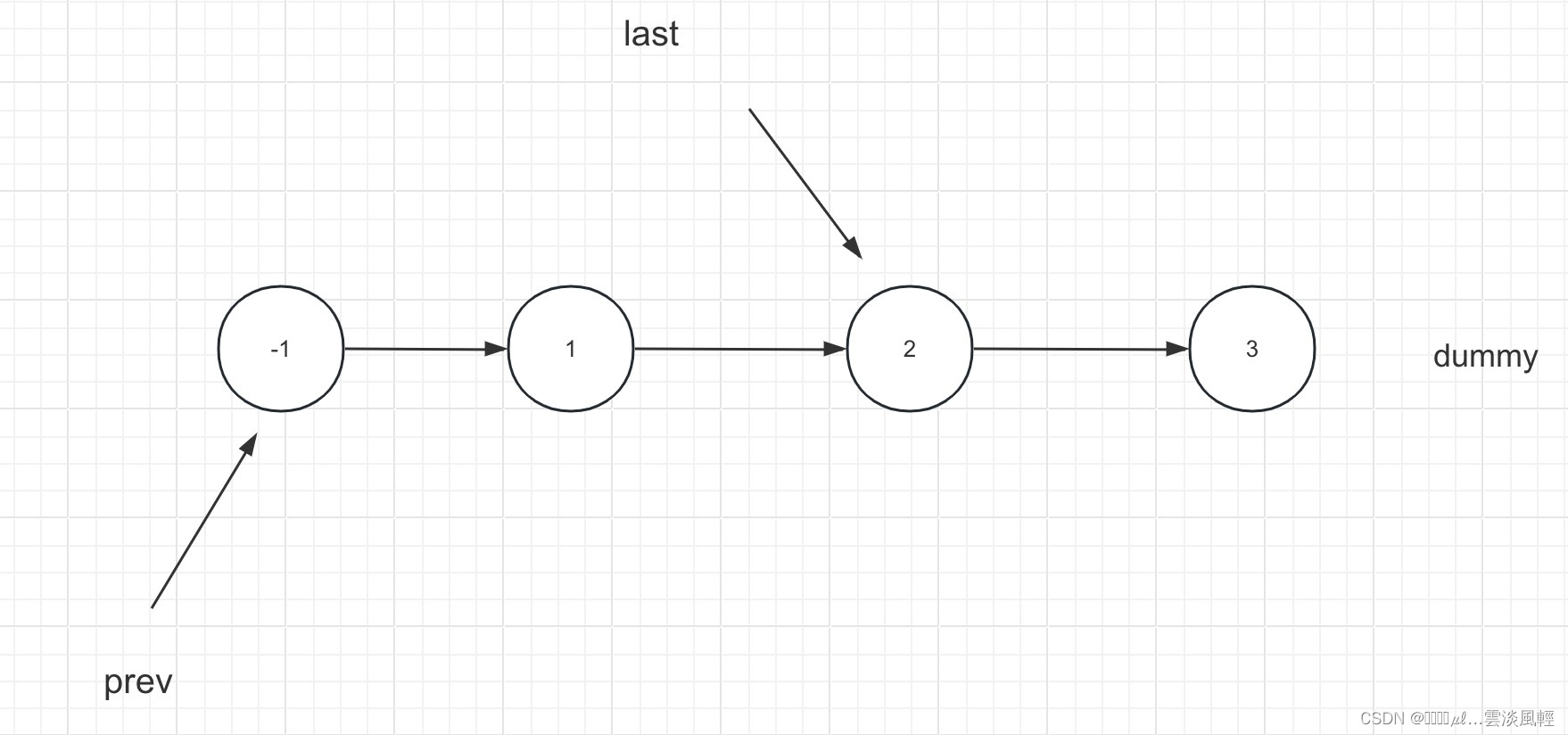
也就是说我们找到了符合K长度的子链表,接下来需要开始对子链表进行翻转了。
增加虚拟节点的好处
还记得前面我们买了一个伏笔吧!那就是为什么要在head原始链表头上加一个虚拟节点。看到这里我想你应该明白了,那就是
- 翻转后的K长子链表需要与旧链表进行缝合,那么就需要知道旧链表的被切割处的节点位置,如果正好是前K个链表,那么翻转后只有尾部需要缝合,前面是没有节点的,难道要在翻转前单独判断无头有尾的特殊情况吗?而在head前面加了虚拟节点则正好解决了这个问题,无论K子链表在dummy哪里,一定都是与旧链表相连的、有头有尾的子链表。
- 如果不存在K长子链表,则直接返回第1个节点就可以了,因为后面的节点会跟着第一个节点,这等于是对于入参head没有操作直接返回了。如果存在K长子链表,翻转后,那么从1到K已经进行了翻转,无论后面又翻转了多少个K子节点,返回的头节点就是K。所以两种情况又要单独判断了。但是加上虚拟节点,无论是否翻转,只需要返回dummy.next即可。
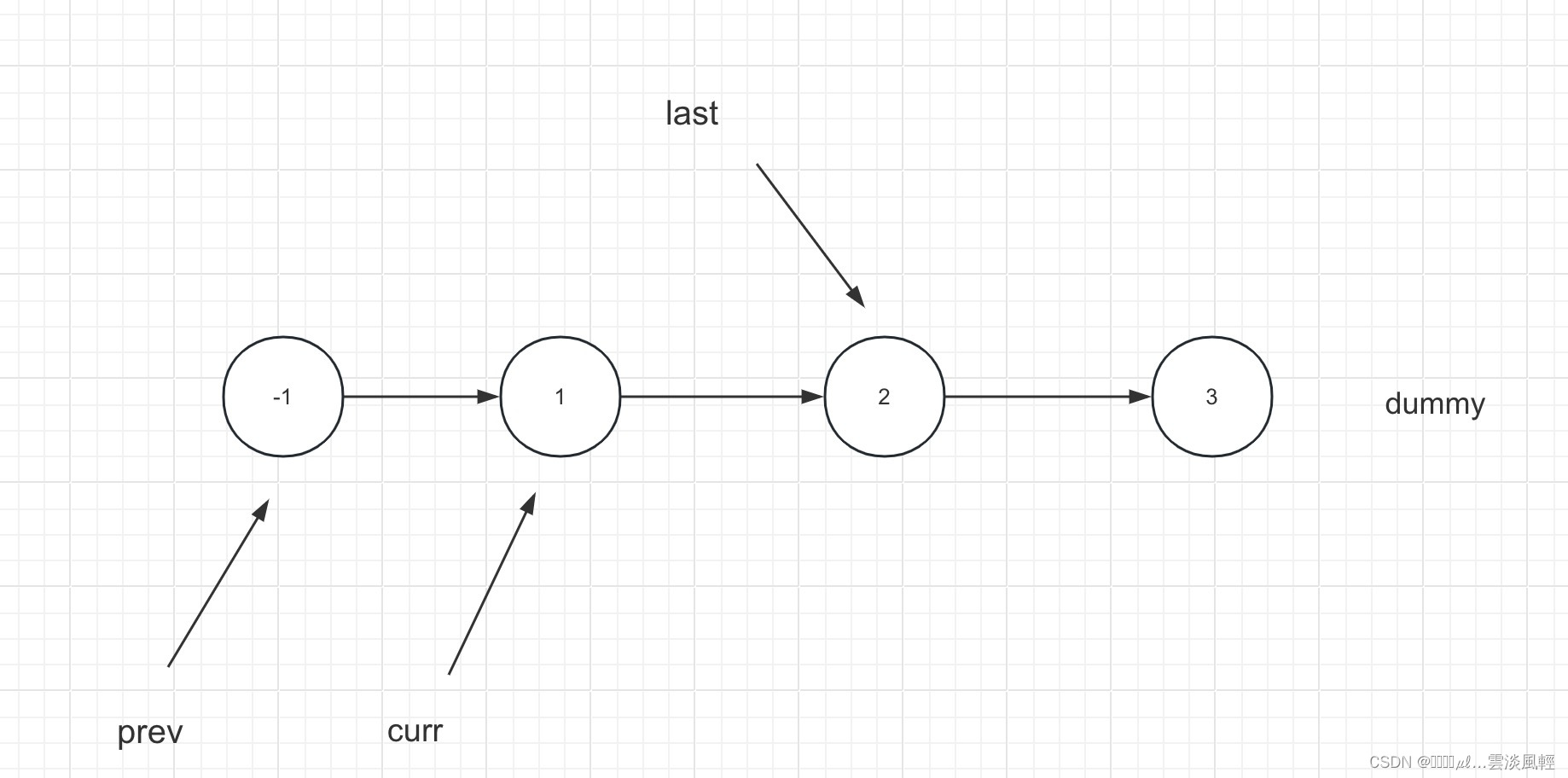
接下来我们看具体翻转K子链表的过程。思考为什么经过翻转后,仍只需要返回dummy.next?(不翻转可以理解,就是dummy.next)
首先要考虑翻转的子链表的起始节点和末尾节点。末尾节点就是last,起始节点应该是prev.next ,因为是动态变化的,需要新加一个指针,姑且称之为curr(意为当前节点),所以K长子链表长度应该从curr到last。
//这里curr的取值不能为 dummy.next,因为prev和curr是随着多个K长子链表动态变化的,而dummy则是一个固定的链表。
ListNode curr = prev.next;
确定了K长子链表,现在对子链表进行翻转,并将翻转后的片段拼接回dummy。
由于K长可变,试想若是存在合理值K=100,那么翻转一次吗?所以翻转的次数也是需要根据K长动态变化的。
// 比如当前假设情况,K=2 ,那么只需要循环一次即可。因为循环一次,翻转了2个节点。同理多个节点道理如此。
for (int i = 0; i < k - 1; i++) {}
翻转实际上就是从K长度子链表的第一个节点curr与下一个节点next进行交换,直至交换到last结束。由于curr会不断在循环后刷新,所以next节点也是随curr节点动态变化的。
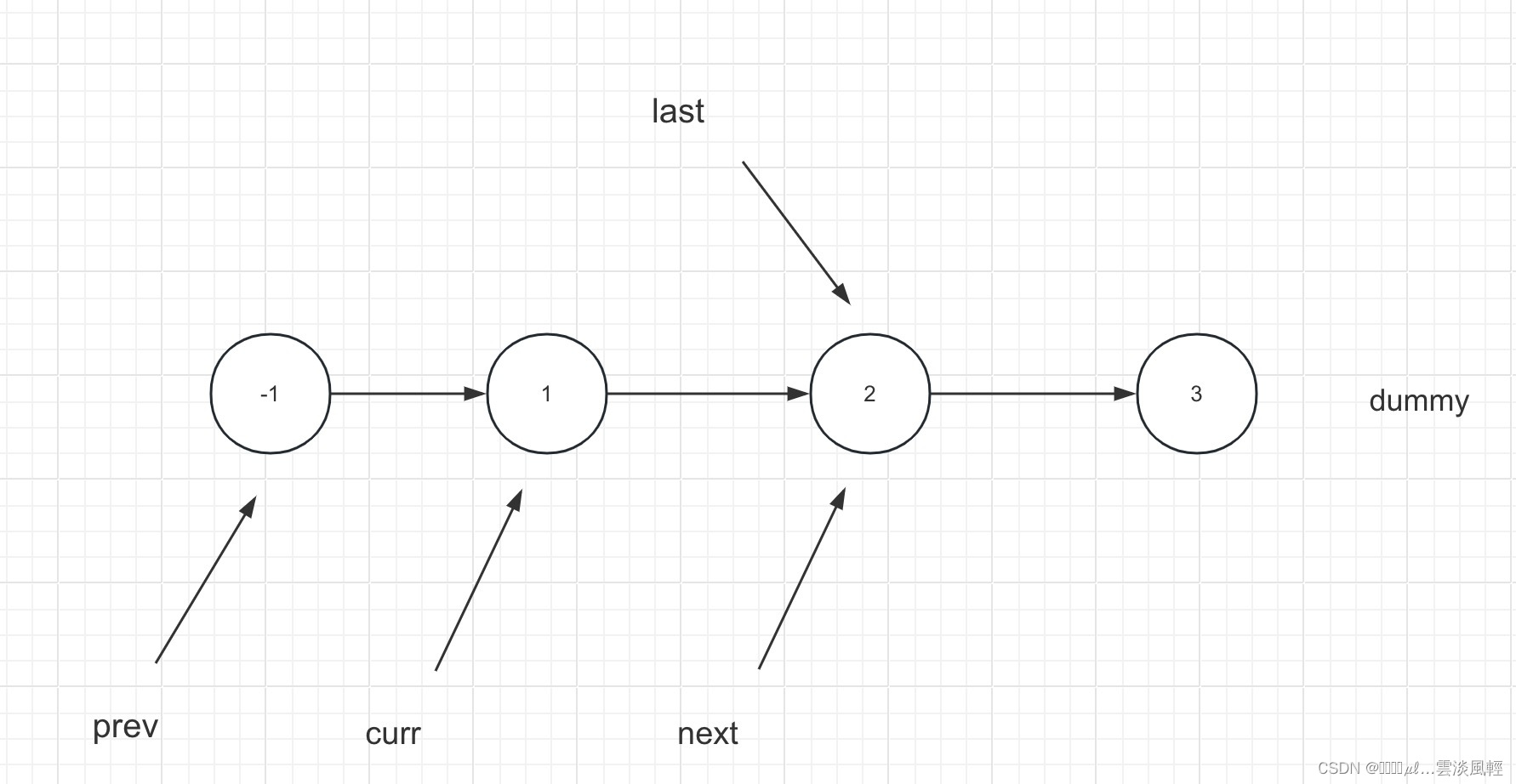
ListNode next = curr.next;
现在我们要做的事情是交换curr节点与next节点,并保证交换后节点与dummy前后开口正确缝合。
- 首先切断curr与next的关联关系,让curr直接跳过next指向next的下一个节点。
//原来curr与next相连,现在这个操作相当于把curr的下个节点跳过了next节点,给到了next下一个节点。
curr.next = next.next;
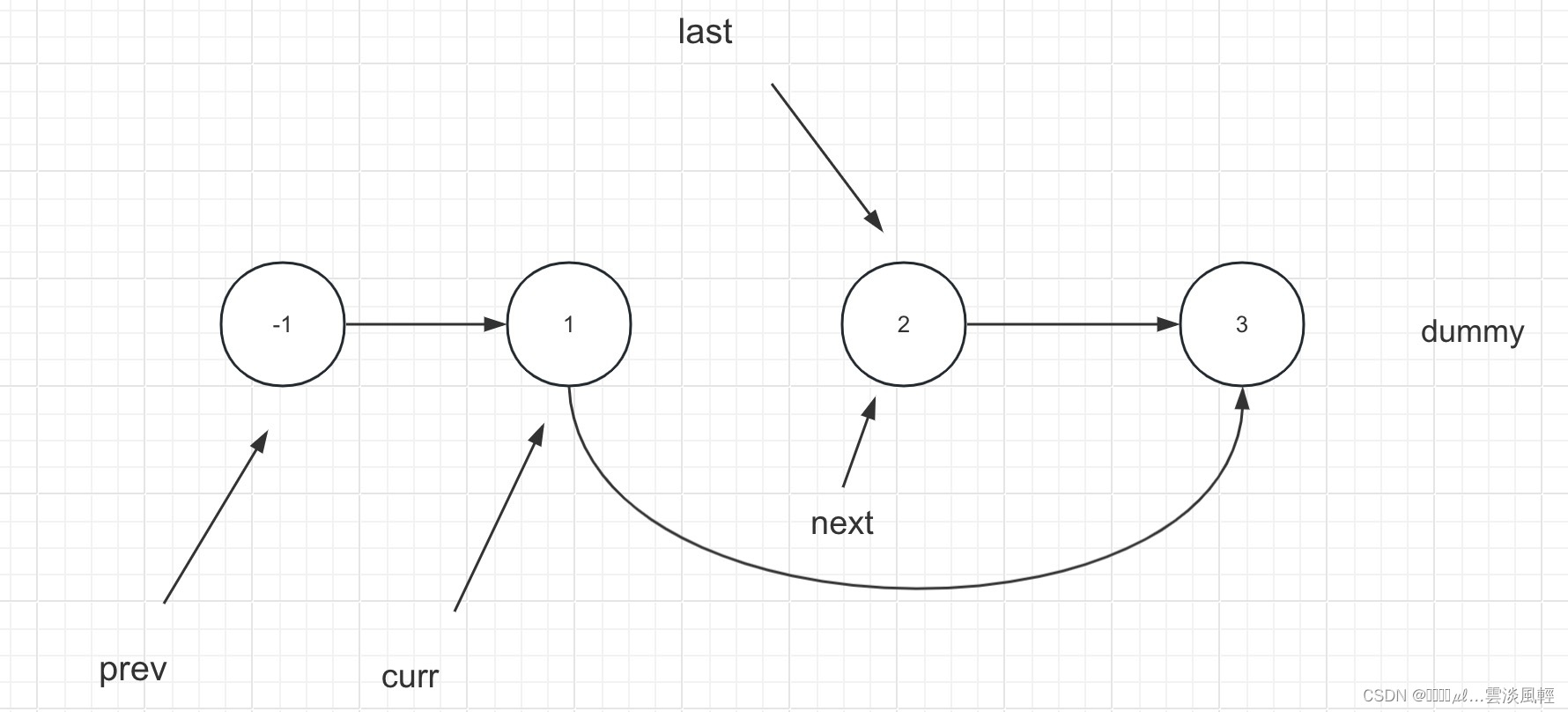
- 将prev节点(K长子链表的头节点)的下一个节点也指向next的下一个节点。
//切断原来next的下一个节点的关联关系,因为上一步进行了1 -> 3 关联, 3节点无需多一个重复被指向,3节点必须是来自于curr的指向。所以把next节点重定向到prev后面。
next.next = prev.next;
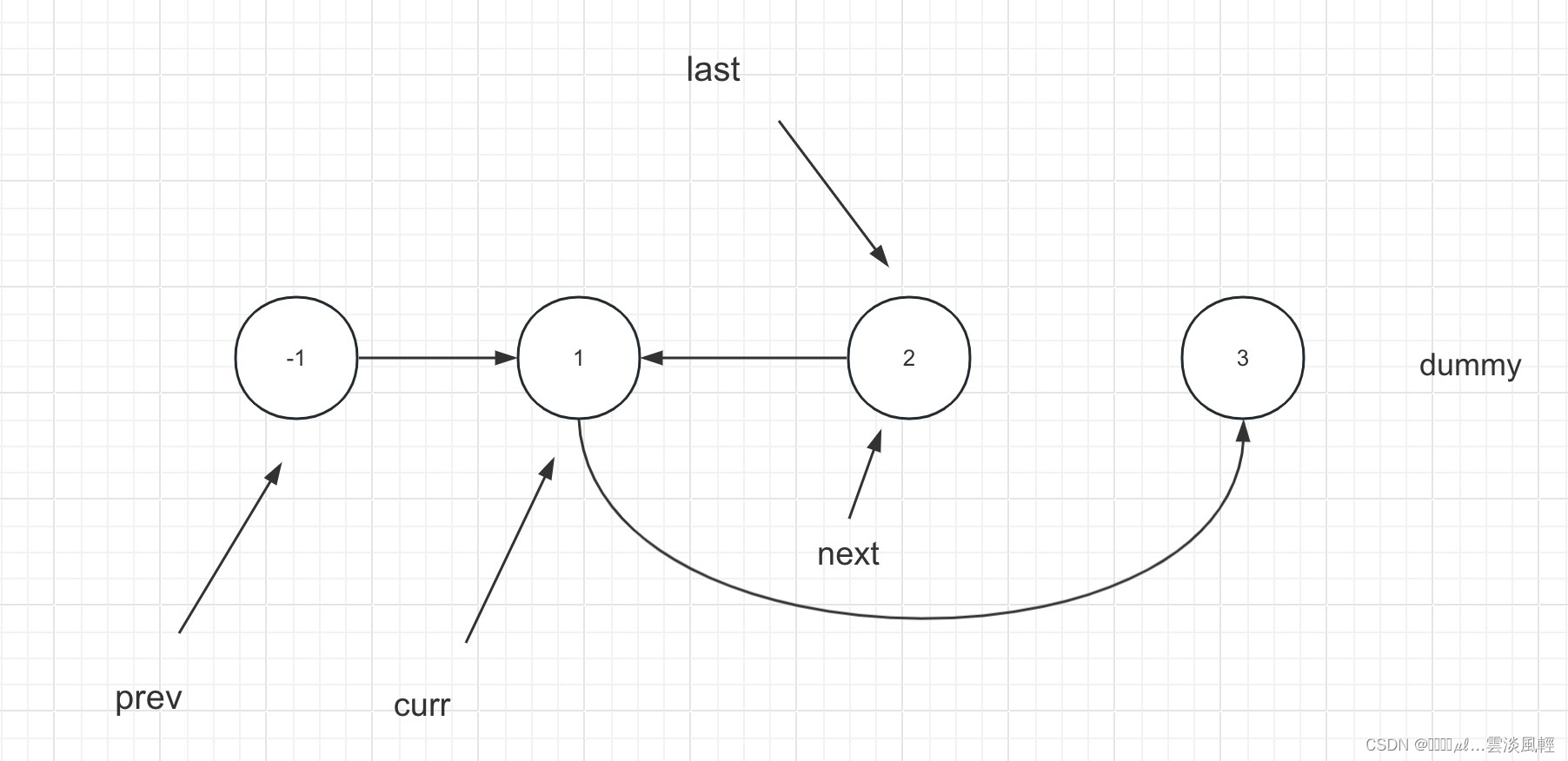
- 将prev节点(K长子链表的头节点)重定向到next节点即可
prev.next = next;
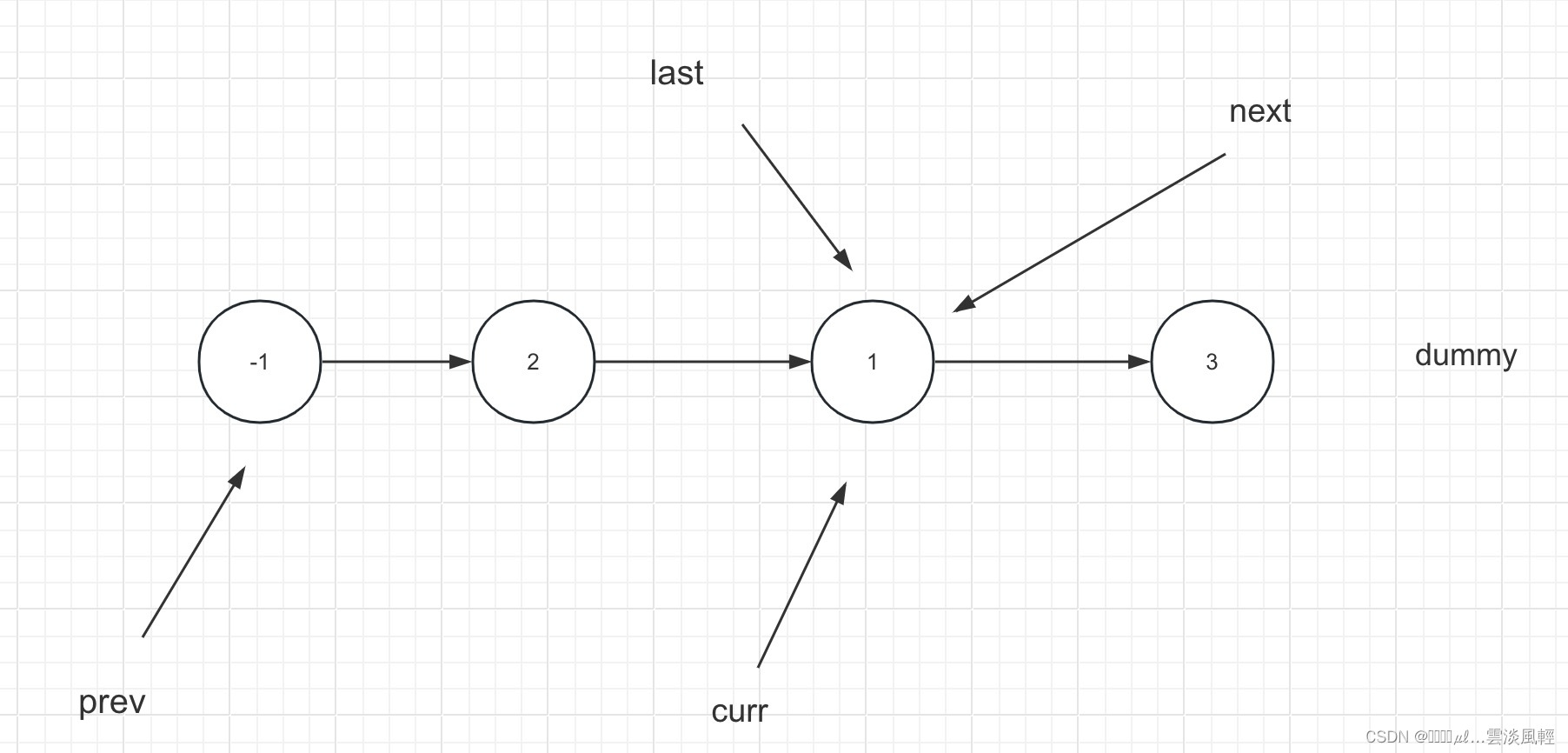
- 将prev(K长子链表的头节点)指向下一轮要进行的K长翻转的头节点处
上面步骤实现了从curr到last的K长一次翻转动作,由于K长子链表需要不断在dummy中遍历寻找是否存在多个K,所以下一次循环K2的时候我们需要将K2的头节点指针重新定位。
//curr一定是K长子链表最末尾的一个节点,所以将prev指针移动到curr节点。
prev = curr;
第二次K循环由于last指针需要移动两次,但是节点3的next为空,所以直接返回prev.next了。
代码梳理
完整代码实现
public static ListNode reverseKGroup(ListNode head, int k) {ListNode dummy = new ListNode(-1, head), prev = dummy;while (true) {// 检查剩余节点是否有k个,不足则返回ListNode last = prev;for (int i = 0; i < k; i++) {last = last.next;if (last == null) {return dummy.next;}}// 翻转k个节点ListNode curr = prev.next, next;for (int i = 0; i < k - 1; i++) {next = curr.next;curr.next = next.next;next.next = prev.next;prev.next = next;}prev = curr;}}public static void main(String[] args) {ListNode list1 = new ListNode(1,new ListNode(2,new ListNode(3)));ListNode listNode = reverseKGroup(list1, 2);//链表遍历while (listNode != null) {System.out.println(listNode.val);listNode = listNode.next;}}
断点步骤拆解
GitHub代码地址
相关文章:

【力扣面试经典150题】(链表)K 个一组翻转链表
题目描述 力扣原文链接 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只…...
数据结构刷题
空间复杂度:临时开辟的空间、空间是可以重复利用的 递归为O(n) 时间复杂度:程序执行次数 消失的数字 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 思路1:利用连续的特点求等差和然后减去所有元素得到的就是消…...

【Android】设置全局标题栏
序言 在做项目的时候,有时候需要一个全局统一的标题栏,保证项目风格的统一,但是如果在每个activity上面都写一遍这个标题栏就很麻烦了,我们经常用的方法就是写个基类Activity,然后当某个Activity需要这个统一的标题栏…...

R语言的入门学习
目录 准备工作导入csv数据集选择前200行作为数据集展示数据集的前/后几N行宏观分析删除缺失值构建直方图导出为图片 R语言常见图像类型例1:散点图例2:散点矩阵图 准备工作 安装教程: R语言和RStudio的下载安装(非常简便舒适&…...

【开源】基于Vue和SpringBoot的民宿预定管理系统
项目编号: S 058 ,文末获取源码。 \color{red}{项目编号:S058,文末获取源码。} 项目编号:S058,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用例设计2.2 功能设计2.2.1 租客角色…...

nacos集群部署
GitHub - nacos-group/nacos-k8s: This project contains a Nacos Docker image meant to facilitate the deployment of Nacos on Kubernetes using StatefulSets. 需要修改两个文件 --- apiVersion: v1 kind: Service metadata:name: nacos-headlessnamespace: project-guli…...

9、传统计算机视觉 —— 边缘检测
本节介绍一种利用传统计算机视觉方法来实现图片边缘检测的方法。 什么是边缘检测? 边缘检测是通过一些算法来识别图像中物体之间,或者物体与背景之间的边界,也就是边缘。 边缘通常是图像中灰度变化显著的地方,标志着不同区域的分界线。 在一张图像中,边缘可以是物体的…...
Linux tc 使用
tc模拟延时丢包等网络故障依赖的内核驱动 /lib/modules/5.15.0-52-generic/kernel/net/sched/sch_netem.ko有些系统并不是默认就安装上该驱动的,如果没有安装该驱动,构造网络故障时会报错。 root:curtis# tc qdisc change dev enp4s0 root netem delay…...

从0开始学习JavaScript--JavaScript 数字与日期
JavaScript中的数字和日期是处理数值计算和时间相关任务的核心。本文将深入研究JavaScript中数字的表示、常见运算,以及日期对象的创建、格式化等操作,并通过丰富的示例代码,可以更全面地了解和应用这些概念。 JavaScript数字基础 JavaScri…...

从关键新闻和最新技术看AI行业发展(2023.11.6-11.19第十期) |【WeThinkIn老实人报】
Rocky Ding 公众号:WeThinkIn 写在前面 【WeThinkIn老实人报】旨在整理&挖掘AI行业的关键新闻和最新技术,同时Rocky会对这些关键信息进行解读,力求让读者们能从容跟随AI科技潮流。也欢迎大家提出宝贵的优化建议,一起交流学习&…...
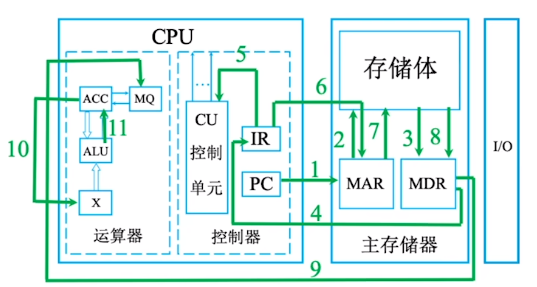
计算机硬件的基本组成
一、冯诺依曼结构 存储程序: “存储程序”的概念是指将指令以二进制代码的形式事先输入计算机的主存储器,然后按其在存储器中的首地址执行程序的第一条指令,以后就按该程序的规定顺序执行其他指令,直至程序执行结束。 冯诺依曼计…...

【算法-哈希表3】四数相加2 和 赎金信
今天,带来哈希表相关算法的讲解。文中不足错漏之处望请斧正! 理论基础点这里 1. 四数相加2 分析题意 求符合条件的四元组的出现次数,条件: nums1nums2nums3nums4 从四个数组中的每一个数组取一个数 num1, num2, num3, num4&am…...
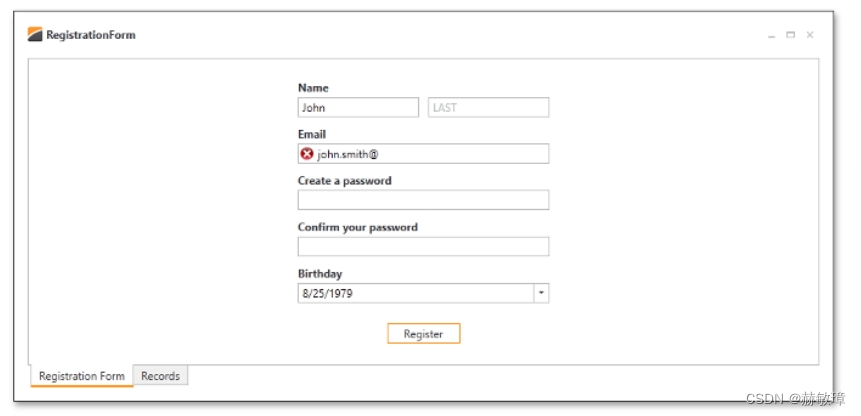
wpf devexpress自定义编辑器
打开前一个例子 步骤1-自定义FirstName和LastName编辑器字段 如果运行程序,会通知编辑器是空。对于例子,这两个未命名编辑器在第一个LayoutItem(Name)。和最终用户有一个访客左右编辑器查阅到First Name和Last Name字段,分别。如果你看到Go…...
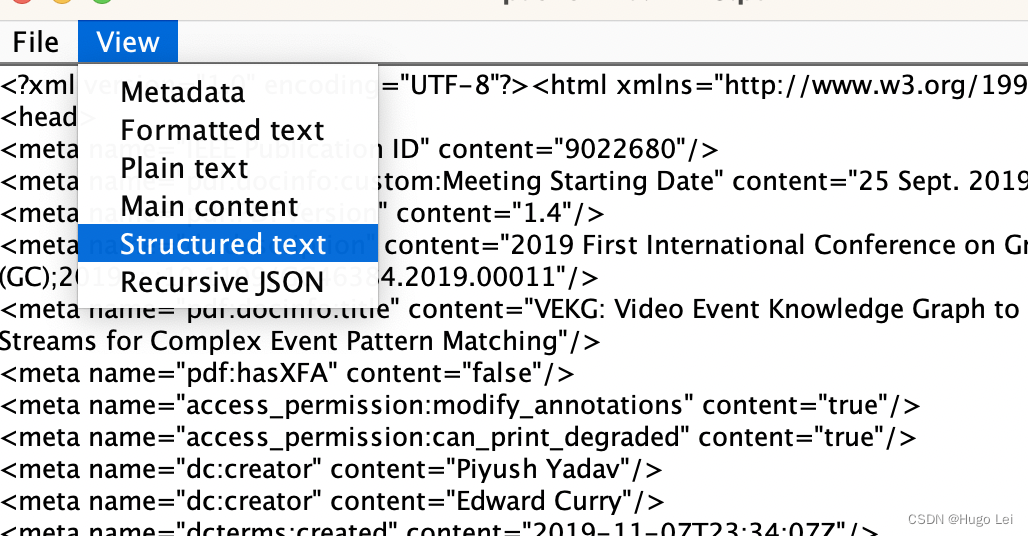
文档向量化工具(一):Apache Tika介绍
Apache Tika是什么?能干什么? Apache Tika是一个内容分析工具包。 该工具包可以从一千多种不同的文件类型(如PPT、XLS和PDF)中检测并提取元数据和文本。 所有这些文件类型都可以通过同一个接口进行解析,这使得Tika在…...

学习c#的第二十一天
目录 C# 泛型(Generic) 泛型类型参数 类型参数的约束 约束多个参数 未绑定的类型参数 类型参数作为约束 notnull 约束 class 约束 default 约束 非托管约束 委托约束 枚举约束 类型参数实现声明的接口 泛型类 泛型方法 泛型和数组 泛型…...

Michael Jordan最新报告:去中心化机器学习中的契约、不确定性和激励
导读 11月3日,智源研究院学术顾问委员会委员、机器学习泰斗Michael Jordan在以“新一代人工智能前沿”为主题的2023北京论坛 新工科专题论坛上,发表了题为Contracts, Uncertainty, and Incentives in Decentralized Machine Learning(去…...

3ds Max渲染用专业显卡还是游戏显卡?
使用3dsmax建模时,会面临诸多选择,除了用vr还是cr的决策,硬件选择上也存在着疑问,比如用专业显卡还是消费级游戏显卡?一般来说,除非是特别专业的大型项目和软件,且预算在5位数以上,常…...
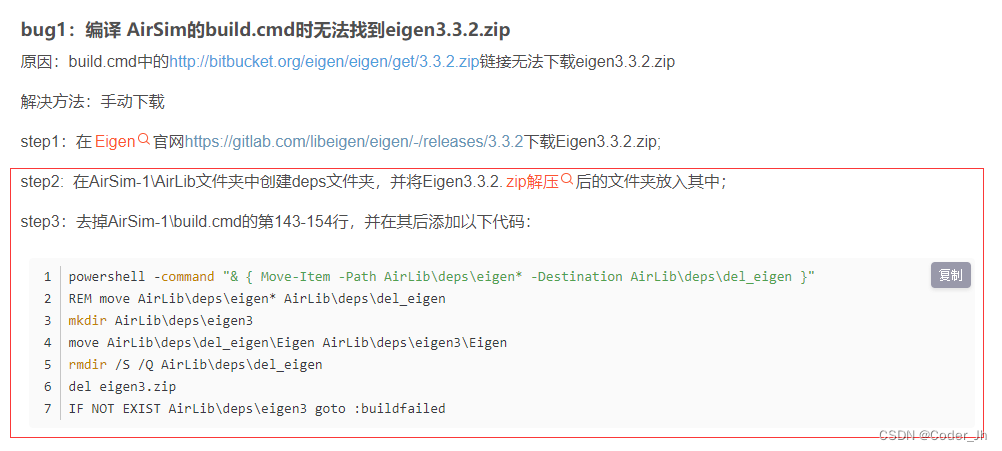
airlearning-ue4安装的踩坑记录
最近要安装airlearning-ue4,用于实现无人机仿真环境,该项目地址为:GitHub - harvard-edge/airlearning-ue4: Environment Generator for Air Learning Project. This version is build on top of UE4 game engine 由于这个项目已经完成好几年…...
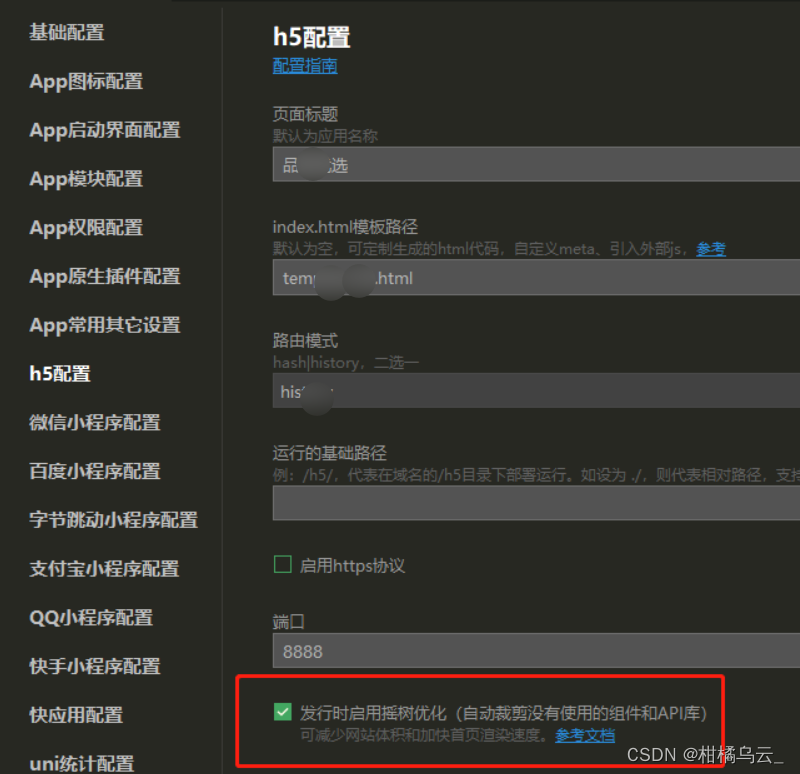
uniapp优化h5项目-摇树优化,gzip压缩和删除console.log
1.摇树优化 勾选摇树优化,打包删除死代码 2.gzip压缩和删除console.log 安装插件webpack和compression-webpack-plugin webpack插件 npm install webpack4.46.0 --save-devcompression-webpack-plugin插件 npm install compression-webpack-plugin6.1.1 --save-devconst Com…...

Pycharm之配置python虚拟环境
最近给身边的人写了脚本,在自己电脑可以正常运行。分享给我身边的人,却运行不起来,然后把报错的截图给我看了,所以难道不会利用pycharm搭建虚拟的环境?记录一下配置的过程。 第一步:右键要打开的python的代…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
