【机器学习12】集成学习
1 集成学习分类
1.1 Boosting
训练基分类器时采用串行的方式, 各个基分类器之间有依赖。每一层在训练的时候, 对前一层基分类器分错的样本, 给予更高的权重。 测试时, 根据各层分类器的结果的加权得到最终结果。
1.2 Bagging
各基分类器之间无强依赖, 可以进行并行训练。 很著名的算法之一是基于决策树基分类器的随机森林(Random Forest) 。为了让基分类器之间互相独立, 将训练集分为若干子集(当训练样本数量较少时, 子集之间可能有交叠) 。 Bagging方法更像是一个集体决策的过程, 每个个体都进行单独学习, 学习的内容可以相同, 也可以不同, 也可以部分重叠。 但由于个体之间存在差异性, 最终做出的判断不会完全一致。 在最终做决策时, 每个个体单独作出判断, 再通过投票的方式做出最后的集体决策。
1.3 基分类器的错误
基分类器的错误,有偏差和方差两种。 偏差主要是由于分类器的表达能力有限导致的系统性错误, 表现在训练误差不收敛。 方差是由于分类器对于样本分布过于敏感, 导致在训练样本数较少时, 产生过拟合。
在有监督学习中, 模型的泛化误差来源于两个方面——偏差和方差, 具体来讲偏差和方差的定义如下:
偏差:偏差指的是由所有采样得到的大小为m的训练数据集训练出的所有模型的输出的平均值和真实模型输出之间的偏差。
方差:方差指的是由所有采样得到的大小为m的训练数据集训练出的所有模型的输出的方差。
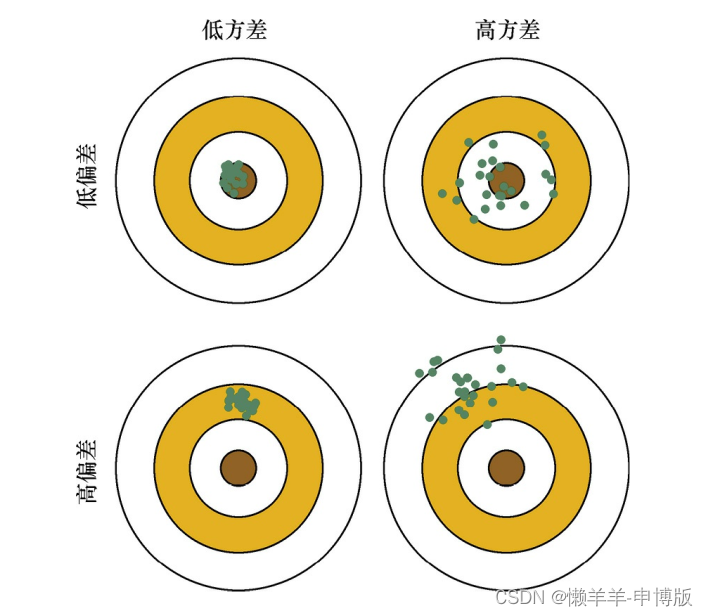
Boosting方法是通过逐步聚焦于基分类器分错的样本, 减小集成分类器的偏差。在训练好一个弱分类器后, 我们需要计算弱分类器的错误或者残差, 作为下一个分类器的输入。 这个过程本身就是在不断减小损失函数, 来使模型不断逼近“靶心”, 使得模型偏差不断降低。
Bagging方法则是采取分而治之的策略, 通过对训练样本多次采样, 并分别训练出多个不同模型, 然后做综合, 来减小集成分类器的方差。对n个独立不相关的模型的预测结果取平均,方差是原来单个模型的1/n。
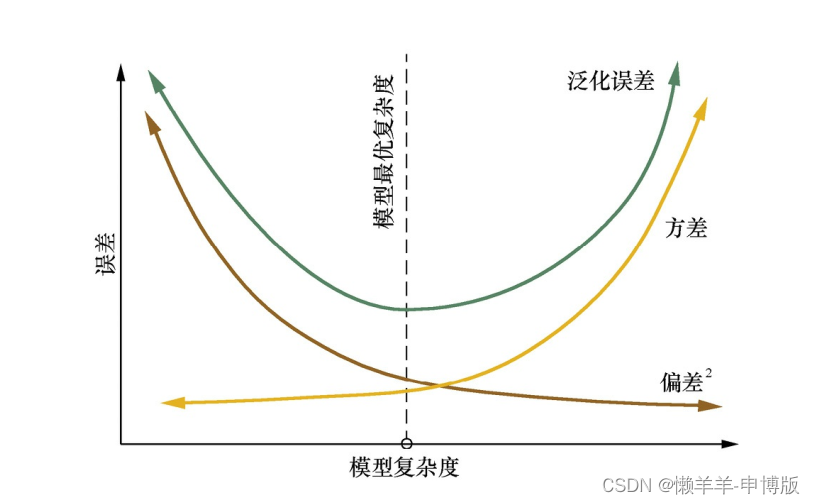
模型复杂度与偏差和方差的关系:
2 集成学习的步骤
(1) 找到误差互相独立的基分类器。
(2) 训练基分类器。
(3) 合并基分类器的结果。
3 基分类器
最常用的基分类器是决策树, 主要有以下3个方面的原因。
(1) 决策树可以较为方便地将样本的权重整合到训练过程中, 而不需要使用过采样的方法来调整样本权重。
(2) 决策树的表达能力和泛化能力, 可以通过调节树的层数来做折中。
(3) 数据样本的扰动对于决策树的影响较大, 因此不同子样本集合生成的决策树基分类器随机性较大, 这样的“不稳定学习器”更适合作为基分类器。 此外,在决策树节点分裂的时候, 随机地选择一个特征子集, 从中找出最优分裂属性,很好地引入了随机性。
除了决策树外, 神经网络模型也适合作为基分类器, 主要由于神经网络模型也比较“不稳定”, 而且还可以通过调整神经元数量、 连接方式、 网络层数、 初始权值等方式引入随机性。
4 梯度提升决策树
4.1 GBDT基本思想
GBDT其基本思想是根据当前模型损失函数的负梯度信息来训练新加入的弱分类器, 然后将训练好的弱分类器以累加的形式结合到现有模型中。采用决策树作为基分类器,使用的决策树通常为CART。
由于GBDT是利用残差训练的, 在预测的过程中, 我们也需要把所有树的预测值加起来, 得到最终的预测结果。
4.2 梯度提升与梯度下降
梯度提升和梯度下降有什么关系?

在梯度下降中, 模型是以参数化形式表示, 从而模型的更新等价于参数的更新。 而在梯度提升中, 模型并不需要进行参数化表示, 而是直接定义在函数空间中。
4.3 GBDT优缺点
优点:
计算速度快;在分布稠密的数据集上, 泛化能力和表达能力都很好;采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性,能够自动发现特征间的高阶关系, 并且也不需要对数据进行特殊的预处理如归一化等。
缺点:
在高维稀疏的数据集上, 表现不如支持向量机或者神经网络;在处理文本分类特征问题上, 相对其他模型的优势不如它在处理数值特征时明显;训练过程需要串行训练, 只能在决策树内部采用一些局部并行的手段提高训练速度。
5 XGBoost
与GBDT不同的是,XGBoost在决策树构建阶段就加入了正则项, 即
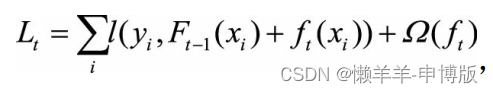
关于树结构的正则项定义为:

从所有的树结构中寻找最优的树结构是一个NP-hard问题, 因此在实际中往往采用贪心法来构建出一个次优的树结构, 基本思想是从根节点开始, 每次对一个叶子节点进行分裂, 针对每一种可能的分裂, 根据特定的准则选取最优的分裂。 不同的决策树算法采用不同的准则, 如IC3算法采用信息增益, C4.5算法为了克服信息增益中容易偏向取值较多的特征而采用信息增益比, CART算法使用基尼指数和平方误差, XGBoost也有特定的准则来选取最优分裂。
分裂前后损失函数的差值为:
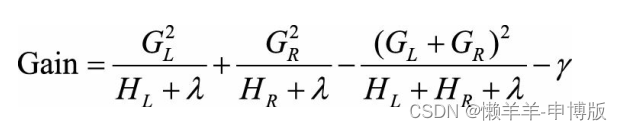
XGBoost采用最大化这个差值作为准则来进行决策树的构建, 通过遍历所有特征的所有取值, 寻找使得损失函数前后相差最大时对应的分裂方式。
(1) GBDT是机器学习算法, XGBoost是该算法的工程实现
(2)在使用CART作为基分类器时, XGBoost显式地加入了正则项来控制模型的复杂度, 有利于防止过拟合, 从而提高模型的泛化能力
(3)GBDT在模型训练时只使用了代价函数的一阶导数信息, XGBoost对代价函数进行二阶泰勒展开, 可以同时使用一阶和二阶导数
(4) 传统的GBDT采用CART作为基分类器, XGBoost支持多种类型的基分类器, 比如线性分类器。
(5) 传统的GBDT在每轮迭代时使用全部的数据, XGBoost则采用了与随机森林相似的策略, 支持对数据进行采样。
(6) 传统的GBDT没有设计对缺失值进行处理, XGBoost能够自动学习出缺失值的处理策略
相关文章:
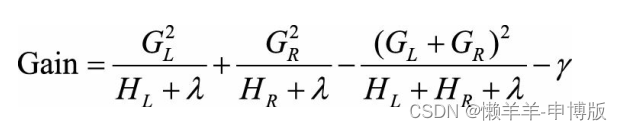
【机器学习12】集成学习
1 集成学习分类 1.1 Boosting 训练基分类器时采用串行的方式, 各个基分类器之间有依赖。每一层在训练的时候, 对前一层基分类器分错的样本, 给予更高的权重。 测试时, 根据各层分类器的结果的加权得到最终结果。 1.2 Bagging …...

nodeJs基础笔记
title: nodeJs基础笔记 date: 2023-11-18 22:33:54 tags: 1. Buffer 1. 概念 Buffer 是一个类似于数组的 对象 ,用于表示固定长度的字节序列。 Buffer 本质是一段内存空间,专门用来处理 二进制数据 。 2. 特点 Buffer 大小固定且无法调整Buffer 性能…...

Skywalking流程分析_9(JDK类库中增强流程)
前言 之前的文章详细介绍了关于非JDK类库的静态方法、构造方法、实例方法的增强拦截流程,本文会详细分析JDK类库中的类是如何被增强拦截的 回到最开始的SkyWalkingAgent#premain try {/** 里面有个重点逻辑 把一些类注入到Boostrap类加载器中 为了解决Bootstrap类…...

矩阵的QR分解
矩阵的QR分解 GramSchmidt 设存在 B { x 1 , x 2 , … , x n } \mathcal{B}\left\{\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right\} B{x1,x2,…,xn}在施密特正交化过程中 q 1 x 1 ∣ ∣ x 1 ∣ ∣ q_1\frac{x_1}{||x_1||} q1∣∣x1∣∣x1 q k …...

STL总结
STL vector 头文件<vector> 初始化,定义,定义长度,定义长度并且赋值,从数组中获取数据返回元素个数size()判断是否为空empty()返回第一个元素front()返回最后一个数back()删除最后一个数pop_back()插入push_back(x)清空clear()begin()end()使用s…...
资深测试总结,现在软件测试有未来吗?“你“的底气在哪里?
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、为什么会有 “…...

Scalable Exact Inference in Multi-Output Gaussian Processes
Orthogonal Instantaneous Linear Mixing Model TY are m-dimensional summaries,ILMM means ‘Instantaneous Linear Mixing Model’,OILMM means ‘Orthogonal Instantaneous Linear Mixing Model’ 辅助信息 作者未提供代码...
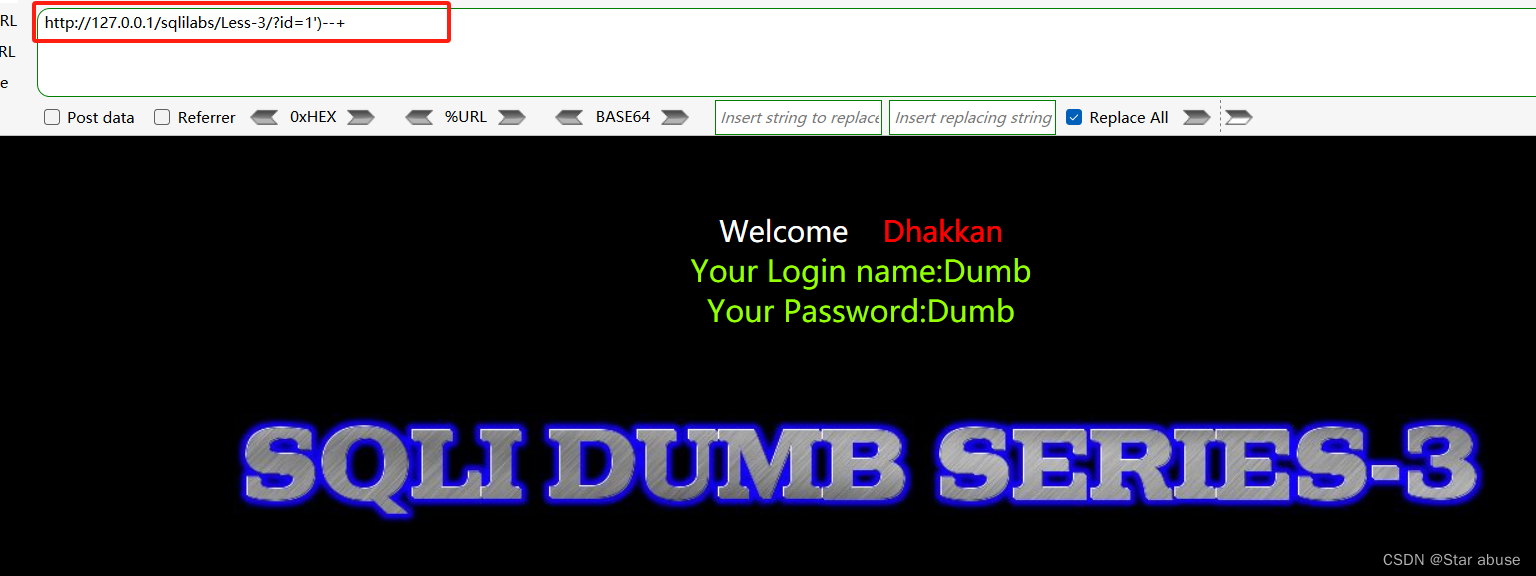
sqli-labs(Less-3)
1. 通过构造id1’ 和id1’) 和id1’)–确定存在注入 可知原始url为 id(‘1’) 2.使用order by 语句猜字段数 http://127.0.0.1/sqlilabs/Less-3/?id1) order by 4 -- http://127.0.0.1/sqlilabs/Less-3/?id1) order by 3 --3. 使用联合查询union select http://127.0.0.1…...

集合框架面试题
一、集合容器的概述 1. 什么是集合 集合框架:用于存储数据的容器。 集合框架是为表示和操作集合而规定的一种统一的标准的体系结构。 任何集合框架都包含三大块内容: 对外的接口、接口的实现和对集合运算的算 法。 接口:表示集合的抽象数据…...

【LeetCode刷题日志】225.用队列实现栈
🎈个人主页:库库的里昂 🎐C/C领域新星创作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:LeetCode 刷题日志🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,…...

【JavaScript】fetch 处理流式数据,实现类 chatgpt 对话
本文只包含最基础的请求后端大佬给得对话接口,大部分模型的传参是差不多的,核心还是如何处理 fetch 获取的流数据 import { defineStore } from pinia; import { ElMessage } from element-plus;type Role system | user | assistant; export interfac…...

收发电子邮件
电子邮件是Internet提供的又一个重要服务项目。早在1987年9月20日,中国首封电子邮件就是从北京经意大利向前联邦德国卡尔斯鲁厄大学发出的,在中国首次实现了与Internet的连接,使中国成为国际互联网大家庭中的一员。现在随着Internet的迅速发展…...
)
sql13(Leetcode570至少有5名直接下属的经理)
代码: 脑子记不住 语法全靠试.. # Write your MySQL query statement below select b.name from (select managerId,count(managerId) as numfrom Employeegroup by managerId ) a left join Employee b on a.managerIdb.id where a.num>5 and b.name is not N…...

15分钟,不,用模板做数据可视化只需5分钟
测试显示,一个对奥威BI软件不太熟悉的人来开发数据可视化报表,要15分钟,而当这个人去套用数据可视化模板做报表,只需5分钟! 数据可视化模板是奥威BI上的一个特色功能板块。用户下载后更新数据源,立即就能获…...

C 语言字符串函数
C 语言字符串函数 在本文中,您将学习使用诸如gets(),puts,strlen()等库函数在C中操作字符串。您将学习从用户那里获取字符串并对该字符串执行操作。 您通常需要根据问题的需要来操作字符串。大多数字符串操作都可以自定义方法完成ÿ…...
nvm安装详细教程(卸载旧的nodejs,安装nvm、node、npm、cnpm、yarn及环境变量配置)
文章目录 一、完全卸载旧的nodejs1、打开系统的控制面板,点击卸载程序,卸载nodejs(1)打开系统的控制面板,点击程序下的卸载程序(2)找到node.js,鼠标右击出现下拉框,点卸载…...
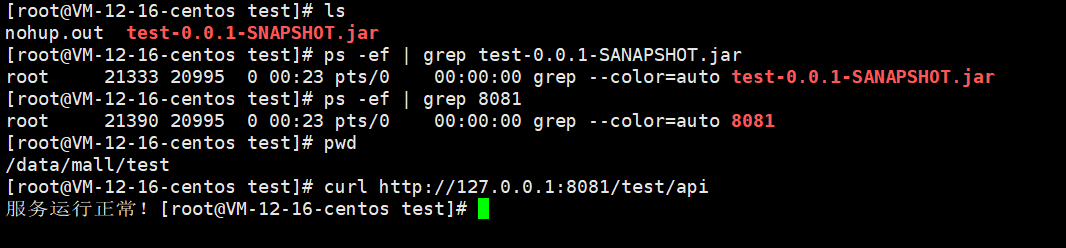
详细步骤记录:持续集成Jenkins自动化部署一个Maven项目
Jenkins自动化部署 提示:本教程基于CentOS Linux 7系统下进行 Jenkins的安装 1. 下载安装jdk11 官网下载地址:https://www.oracle.com/cn/java/technologies/javase/jdk11-archive-downloads.html 本文档教程选择的是jdk-11.0.20_linux-x64_bin.tar.g…...
Python学习(一)基础语法
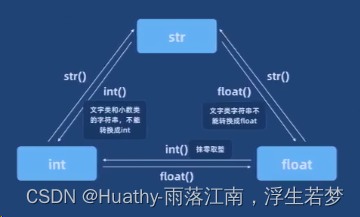
文章目录 1. 入门1.1 解释器的作用1.2 下载1.3 基础语法输入输出语法与引号注释:变量: 数据类型与四则运算数据类型四则运算数据类型的查看type()数据类型的转换int()、int()、float() 流程控制格式化输出循环与遍历逻辑运算符list遍历字典dict遍历 跳出…...

【C刷题】day7
🎥 个人主页:深鱼~🔥收录专栏:【C】每日一练🌄欢迎 👍点赞✍评论⭐收藏 一、选择题 1、以下对C语言函数的有关描述中,正确的有【多选】( ) A: 在C语言中,一…...
数据挖掘复盘——apriori
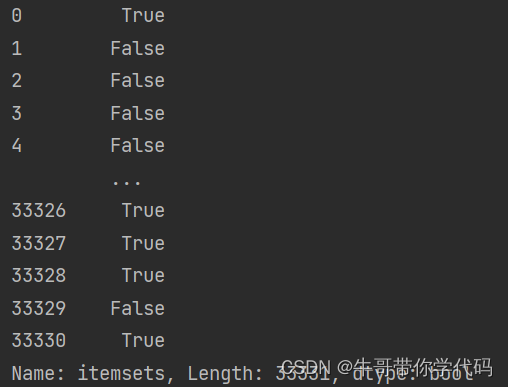
read_csv函数返回的数据类型是Dataframe类型 对于Dataframe类型使用条件表达式 dfdf.loc[df.loc[:,0]2]df: 这是一个DataFrame对象的变量名,表示一个二维的表格型数据结构,类似于电子表格或SQL表。 df.loc[:, 0]: 这是使用DataFrame的.loc属性来进行…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
