CSDN每日一题学习训练——Python版(搜索插入位置、最大子序和)
版本说明
当前版本号[20231118]。
| 版本 | 修改说明 |
|---|---|
| 20231118 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 搜索插入位置
- 题目
- 解题思路
- 代码思路
- 参考代码
- 最大子序和
- 题目
- 解题思路
- 代码思路
- 参考代码
搜索插入位置
题目
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
解题思路
- 初始化左右指针l和r,分别指向数组的第一个元素和最后一个元素。
- 当左指针小于右指针时,执行以下操作:
a. 计算中间位置mid。
b. 如果中间位置的元素小于目标值,将左指针移动到mid+1。
c. 否则,将右指针移动到mid。 - 当循环结束时,检查左指针所指的元素是否小于目标值。如果是,则返回左指针+1;否则,返回左指针。
代码思路
-
定义一个名为Solution的类。
-
在Solution类中定义一个名为searchInsert的方法,接收两个参数:nums和target。其中nums是有序数组,target是要查找的目标值。
# 定义一个名为searchInsert的方法,接收两个参数:nums和targetdef searchInsert(self, nums, target): -
初始化左右指针l和r,分别指向数组的第一个元素和最后一个元素。
# 初始化左右指针l和rl, r = int(0), len(nums) - 1 -
当左指针小于右指针时,执行循环。
-
计算中间位置mid。
# 计算中间位置midmid = int((l + r) / 2) -
如果中间位置的值小于目标值,则将左指针移动到中间位置的右侧;否则,将右指针移动到中间位置。
# 如果中间位置的值小于目标值,则将左指针移动到中间位置的右侧if nums[mid] < target:l = mid + 1# 否则,将右指针移动到中间位置else:r = mid -
循环结束后,如果左指针所指的值小于目标值,则返回左指针的右侧位置加1;否则,返回左指针所指的位置。
# 如果左指针所指的值小于目标值,则返回左指针的右侧位置加1if nums[l] < target:return l + 1# 否则,返回左指针所指的位置return l -
如果当前模块是主模块,则创建一个Solution类的实例s,并调用searchInsert方法,打印结果。
# 如果当前模块是主模块,则执行以下代码
if __name__ == '__main__':# 创建一个Solution类的实例ss = Solution()# 调用searchInsert方法,并打印结果print(s.searchInsert([1,3,5,6],5))
参考代码
这段代码是一个二分查找算法的实现,用于在一个有序数组中查找目标值应该插入的位置。
class Solution:def searchInsert(self, nums, target):l, r = int(0), len(nums) - 1while l < r:mid = int((l + r) / 2)if nums[mid] < target:l = mid + 1else:r = midif nums[l] < target:return l + 1return l
if __name__ == '__main__':s = Solution()print (s.searchInsert([1,3,5,6],5))
最大子序和
题目
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [0]
输出:0
示例 4:
输入:nums = [-1]
输出:-1
示例 5:
输入:nums = [-100000]
输出:-100000
提示:
1 <= nums.length <= 3 * 104
-105 <= nums[i] <= 105
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
解题思路
- 初始化两个变量 maxEndingHere 和 maxSofFar,分别解题思路:
- 初始化两个变量 maxEndingHere 和 maxSofFar,分别表示以当前元素结尾的最大子数组和和全局最大子数组和。初始值都设为数组的第一个元素。
- 遍历数组中除第一个元素之外的其他元素。
- 对于每个元素,更新 maxEndingHere 的值。maxEndingHere 的更新规则是:取 maxEndingHere + nums[i] 和 nums[i] 中的较大值。这样可以保证 maxEndingHere 始终表示以当前元素结尾的最大子数组和。
- 同时更新 maxSofFar 的值。maxSofFar 的更新规则是:取 maxEndingHere 和 maxSofFar 中的较大值。这样可以保证 maxSofFar 始终表示全局最大子数组和。
- 遍历结束后,返回 maxSofFar 作为结果。
代码思路
-
定义一个名为Solution的类,继承自object。
-
在Solution类中定义一个名为maxSubArray的方法,接收一个参数nums。
# 定义一个名为maxSubArray的方法,接收一个参数numsdef maxSubArray(self, nums): -
初始化两个变量maxEndingHere和maxSofFar,分别赋值为nums的第一个元素。
# 初始化两个变量maxEndingHere和maxSofFar,分别赋值为nums的第一个元素maxEndingHere = maxSofFar = nums[0] -
遍历nums列表中从第二个元素开始的所有元素。
# 遍历nums列表中从第二个元素开始的所有元素for i in range(1, len(nums)): -
对于每个元素,更新maxEndingHere的值,取当前值与nums[i]之和与nums[i]中的较大值。
# 更新maxEndingHere的值,取当前值与nums[i]之和与nums[i]中的较大值maxEndingHere = max(maxEndingHere + nums[i], nums[i]) -
同时更新maxSofFar的值,取maxEndingHere与maxSofFar中的较大值。
# 更新maxSofFar的值,取maxEndingHere与maxSofFar中的较大值maxSofFar = max(maxEndingHere, maxSofFar) -
遍历结束后,返回maxSofFar的值,即为整个数组的最大子数组和。
-
创建一个Solution类的实例s。
-
调用s的maxSubArray方法,传入参数nums,并打印结果。
# 创建一个Solution类的实例s s = Solution() # 调用s的maxSubArray方法,传入参数nums,并打印结果 print(s.maxSubArray(nums = [-2,1,-3,4,-1,2,1,-5,4]))
参考代码
这段代码是一个求解最大子数组和的算法。它使用了动态规划的思想,通过遍历数组并不断更新当前最大子数组和(maxEndingHere)和全局最大子数组和(maxSofFar),最终得到整个数组的最大子数组和。
class Solution(object):def maxSubArray(self, nums):maxEndingHere = maxSofFar = nums[0]for i in range(1, len(nums)):maxEndingHere = max(maxEndingHere + nums[i], nums[i])maxSofFar = max(maxEndingHere, maxSofFar)return maxSofFar
# %%
s = Solution()
print(s.maxSubArray(nums = [-2,1,-3,4,-1,2,1,-5,4]))
相关文章:
)
CSDN每日一题学习训练——Python版(搜索插入位置、最大子序和)
版本说明 当前版本号[20231118]。 版本修改说明20231118初版 目录 文章目录 版本说明目录搜索插入位置题目解题思路代码思路参考代码 最大子序和题目解题思路代码思路参考代码 搜索插入位置 题目 给定一个排序数组和一个目标值,在数组中找到目标值,…...

Java在物联网中的重要性
【点我-这里送书】 本人详解 作者:王文峰,参加过 CSDN 2020年度博客之星,《Java王大师王天师》 公众号:JAVA开发王大师,专注于天道酬勤的 Java 开发问题中国国学、传统文化和代码爱好者的程序人生,期待你的关注和支持!本人外号:神秘小峯 山峯 转载说明:务必注明来源(…...

动态规划解背包问题
题目 题解 def knapsac(W: int, N: int, wt: List[int], val: List[int]) -> int:# 定义状态动作价值函数: dp[i][j],对于前i个物品,当前背包容量为j,最大的可装载价值dp [[0 for j in range(W1)] for i in range(N1)]# 状态动作转移for…...

PCL内置点云类型
PCL内置了许多点云类型供我们使用,下面先介绍PLC内置的点云数据类型 PCL中的点云类型为PointT;至于为什么是PointT类型需要追随到原来的ros开发中去,因为PCL库也是从原来的ROS中剥离出来的;大家都一致的认为点云结构是离散的N维信…...

clickhouse数据结构和常用数据操作
背景, 大数据中查询用mysql时间太长, 使用clickhouse 速度快, 数据写入mysql后同步到clickhouse中 测试1千万数据模糊搜索 mysql 需要30-40秒 clickhouse 约 100ms 一 数据结构和存储引擎 1 查看clickhouse所有数据类型 select * from system.data_type_families; 2 …...
upload-labs关卡9(基于win特性data流绕过)通关思路
文章目录 前言一、靶场需要了解的知识1::$data是什么 二、靶场第九关通关思路1、看源码2、bp抓包修改后缀名3、检查是否成功上传 总结 前言 此文章只用于学习和反思巩固文件上传漏洞知识,禁止用于做非法攻击。注意靶场是可以练习的平台,不能随意去尚未授…...

C++过河卒问题
#include <iostream> #include <cstring> using namespace std;int board[20][20]; // 棋盘 int dp[20][20][20][20]; // 动态规划数组int main() {int x0, y0, x1, y1;cin >> x0 >> y0 >> x1 >> y1; // 输入卒的起点和终点memset(board,…...
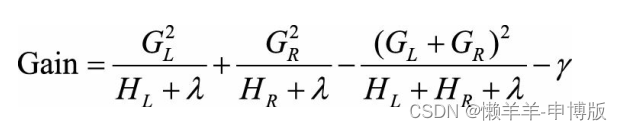
【机器学习12】集成学习
1 集成学习分类 1.1 Boosting 训练基分类器时采用串行的方式, 各个基分类器之间有依赖。每一层在训练的时候, 对前一层基分类器分错的样本, 给予更高的权重。 测试时, 根据各层分类器的结果的加权得到最终结果。 1.2 Bagging …...

nodeJs基础笔记
title: nodeJs基础笔记 date: 2023-11-18 22:33:54 tags: 1. Buffer 1. 概念 Buffer 是一个类似于数组的 对象 ,用于表示固定长度的字节序列。 Buffer 本质是一段内存空间,专门用来处理 二进制数据 。 2. 特点 Buffer 大小固定且无法调整Buffer 性能…...

Skywalking流程分析_9(JDK类库中增强流程)
前言 之前的文章详细介绍了关于非JDK类库的静态方法、构造方法、实例方法的增强拦截流程,本文会详细分析JDK类库中的类是如何被增强拦截的 回到最开始的SkyWalkingAgent#premain try {/** 里面有个重点逻辑 把一些类注入到Boostrap类加载器中 为了解决Bootstrap类…...

矩阵的QR分解
矩阵的QR分解 GramSchmidt 设存在 B { x 1 , x 2 , … , x n } \mathcal{B}\left\{\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right\} B{x1,x2,…,xn}在施密特正交化过程中 q 1 x 1 ∣ ∣ x 1 ∣ ∣ q_1\frac{x_1}{||x_1||} q1∣∣x1∣∣x1 q k …...

STL总结
STL vector 头文件<vector> 初始化,定义,定义长度,定义长度并且赋值,从数组中获取数据返回元素个数size()判断是否为空empty()返回第一个元素front()返回最后一个数back()删除最后一个数pop_back()插入push_back(x)清空clear()begin()end()使用s…...
资深测试总结,现在软件测试有未来吗?“你“的底气在哪里?
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、为什么会有 “…...

Scalable Exact Inference in Multi-Output Gaussian Processes
Orthogonal Instantaneous Linear Mixing Model TY are m-dimensional summaries,ILMM means ‘Instantaneous Linear Mixing Model’,OILMM means ‘Orthogonal Instantaneous Linear Mixing Model’ 辅助信息 作者未提供代码...
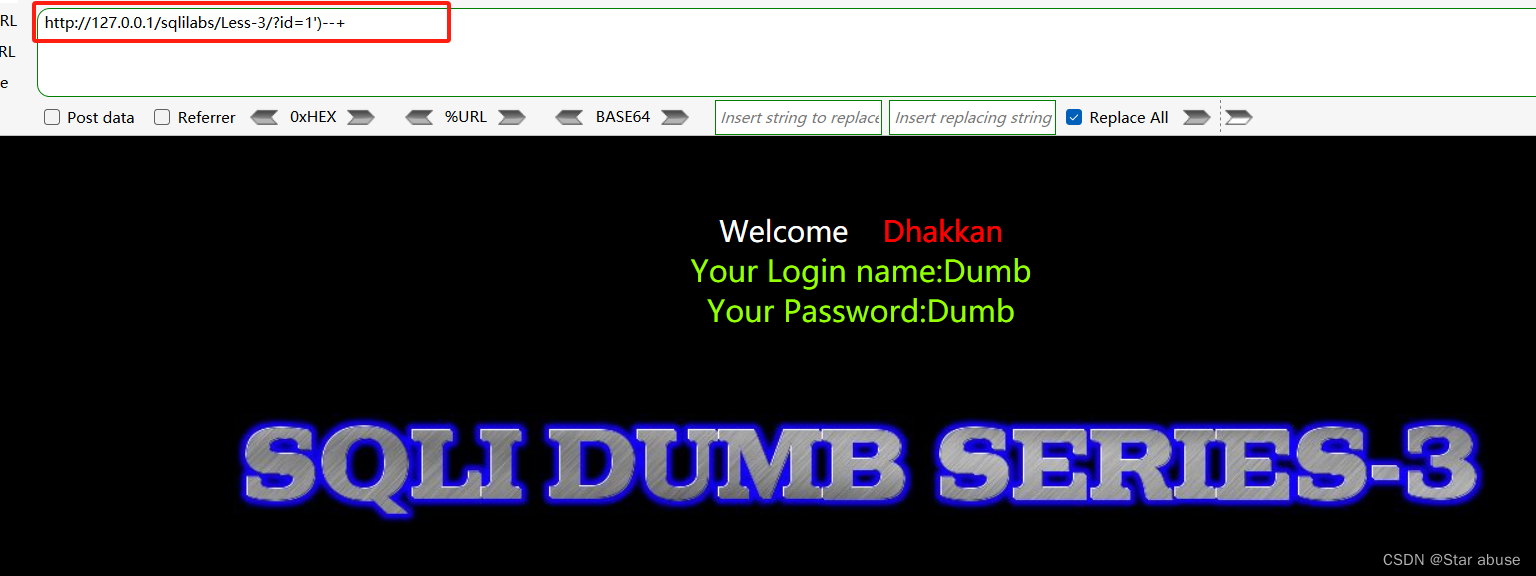
sqli-labs(Less-3)
1. 通过构造id1’ 和id1’) 和id1’)–确定存在注入 可知原始url为 id(‘1’) 2.使用order by 语句猜字段数 http://127.0.0.1/sqlilabs/Less-3/?id1) order by 4 -- http://127.0.0.1/sqlilabs/Less-3/?id1) order by 3 --3. 使用联合查询union select http://127.0.0.1…...

集合框架面试题
一、集合容器的概述 1. 什么是集合 集合框架:用于存储数据的容器。 集合框架是为表示和操作集合而规定的一种统一的标准的体系结构。 任何集合框架都包含三大块内容: 对外的接口、接口的实现和对集合运算的算 法。 接口:表示集合的抽象数据…...

【LeetCode刷题日志】225.用队列实现栈
🎈个人主页:库库的里昂 🎐C/C领域新星创作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:LeetCode 刷题日志🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,…...

【JavaScript】fetch 处理流式数据,实现类 chatgpt 对话
本文只包含最基础的请求后端大佬给得对话接口,大部分模型的传参是差不多的,核心还是如何处理 fetch 获取的流数据 import { defineStore } from pinia; import { ElMessage } from element-plus;type Role system | user | assistant; export interfac…...

收发电子邮件
电子邮件是Internet提供的又一个重要服务项目。早在1987年9月20日,中国首封电子邮件就是从北京经意大利向前联邦德国卡尔斯鲁厄大学发出的,在中国首次实现了与Internet的连接,使中国成为国际互联网大家庭中的一员。现在随着Internet的迅速发展…...
)
sql13(Leetcode570至少有5名直接下属的经理)
代码: 脑子记不住 语法全靠试.. # Write your MySQL query statement below select b.name from (select managerId,count(managerId) as numfrom Employeegroup by managerId ) a left join Employee b on a.managerIdb.id where a.num>5 and b.name is not N…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
