核—幂零分解
若向量空间 V \mathcal V V存在子空间 X \mathcal X X与 Y \mathcal Y Y,当
X + Y = V X ∩ Y = 0 \mathcal {X\text{+}Y\text{=}V}\\ \mathcal {X}\cap \mathcal {Y}=0 X+Y=VX∩Y=0
时称子空间 X \mathcal X X与 Y \mathcal Y Y是完备的,其中记为 X ⊕ Y = V \mathcal X \oplus \mathcal Y = \mathcal V X⊕Y=V
若存在 X ⊕ Y = V \mathcal X \oplus \mathcal Y = \mathcal V X⊕Y=V, 对于 x ∈ X , y ∈ Y , v ∈ V x\in \mathcal X,y \in \mathcal Y,v \in \mathcal V x∈X,y∈Y,v∈V,满足 v = x + y v=x+y v=x+y,则向量 x x x被称为向量 v v v沿着 Y \mathcal Y Y到 X \mathcal X X 空间的投影,向量 y y y被称为向量 v v v沿着 X \mathcal X X到 Y \mathcal Y Y 空间的投影,若存在 P v = x Pv=x Pv=x, P P P被称为沿着 Y \mathcal Y Y到 X \mathcal X X 空间的投影算子,其中
- P 2 = P P^2=P P2=P
- 1 − P 1-P 1−P沿着 X \mathcal X X到 Y \mathcal Y Y 空间的投影算子
- R ( P ) = N ( 1 − P ) = X R(P)=N(1-P)=\mathcal X R(P)=N(1−P)=X
- N ( P ) = R ( 1 − P ) = Y N(P)=R(1-P)=\mathcal Y N(P)=R(1−P)=Y
若 V = R n V=\mathfrak R^n V=Rn,则 P [ X ∣ Y ] = [ X ∣ 0 ] P[\mathbf X|\mathbf Y]=[\mathbf X|\mathbf 0] P[X∣Y]=[X∣0],即 P = [ X ∣ 0 ] [ X ∣ Y ] − 1 = [ X ∣ 0 ] ( I 0 0 0 ) [ X ∣ Y ] − 1 P=[\mathbf X|\mathbf 0][\mathbf X|\mathbf Y]^{-1}=[\mathbf X|\mathbf 0]\begin{pmatrix}\mathbf I&\mathbf0\\\mathbf 0&\mathbf 0\end{pmatrix}[\mathbf X|\mathbf Y]^{-1} P=[X∣0][X∣Y]−1=[X∣0](I000)[X∣Y]−1,其中 X , Y \mathbf X,\mathbf Y X,Y分别表示 X , Y \mathcal X ,\mathcal Y X,Y的一组基
值域零空间分解
若存在一个k,满足 rank ( A k ) = rank ( A k + 1 ) \text{rank}(A^k)=\text{rank}(A^{k+1}) rank(Ak)=rank(Ak+1),则将最小的那个k值称为index,其中非奇异矩阵的index为0
对于奇异矩阵 A n × n A_{n\times n} An×n,存在一个index k,使得$R(A^k)\oplus N(A^k)=\mathfrak R^n $
若存在一个矩阵 A k = 0 A^k=0 Ak=0,其中index(A)=0,则矩阵A被称为幂零矩阵
核—幂零分解
如果A是一个 n × n n\times n n×n 的index为k的奇异矩阵,其中 rank ( A k ) = r \text{rank}(A^k)=r rank(Ak)=r,则存在一个非奇异矩阵 Q Q Q, 满足
Q − 1 A Q = ( C r × r 0 0 N ) \left.\mathbf{Q}^{-1}\mathbf{A}\mathbf{Q}=\left(\begin{array}{cc}\mathbf{C}_{r\times r}&\mathbf{0}\\\mathbf{0}&\mathbf{N}\end{array}\right.\right) Q−1AQ=(Cr×r00N)
其中 C C C是非奇异矩阵, N N N是index为k的幂零矩阵,其中 Q Q Q为矩阵 A k A^k Ak的值域空间和零空间的基的组合
若存在 A = Q ( C 0 0 N ) Q − 1 \left.\mathbf{A}=\mathbf{Q}\left(\begin{array}{ll}\mathbf{C}&0\\0&\mathbf{N}\end{array}\right.\right)\mathbf{Q}^{-1} A=Q(C00N)Q−1,则 A D = Q ( C − 1 0 0 0 ) Q − 1 \left.\mathbf{A}^D=\mathbf{Q}\left(\begin{array}{ll}\mathbf{C}^{-1}&0\\0&0\end{array}\right.\right)\mathbf{Q}^{-1} AD=Q(C−1000)Q−1,其中 A D A^D AD被称为A的广义逆
对于矩阵 A = ( − 2 0 − 4 4 2 4 3 2 2 ) \left.\textbf{A}=\left(\begin{array}{rrr}-2&0&-4\\4&2&4\\3&2&2\end{array}\right.\right) A= −243022−442 ,计算出 core-nilpoten 的分解形式,并给出对应的 Drazin 逆的形式。
直接计算可得 : r a n k ( A ) = 2 , r a n k ( A 2 ) = 1 , r a n k ( A 3 ) = 1 :\:rank(\mathbf{A})=2,\:rank(\mathbf{A^2})=1,\:rank(\mathbf{A^3})=1 :rank(A)=2,rank(A2)=1,rank(A3)=1, 由此可知 : i n d e x ( A ) = 2. :index(\mathbf{A})=2. :index(A)=2. 由 core-nilpotent 分解可知,矩阵 Q = [ X ∣ Y ] \mathbf{Q}=[\mathbf{X}|\mathbf{Y}] Q=[X∣Y], 这里 X \mathbf{X} X 和 Y 分别为 R ( A 2 ) R(\mathbf{A}^2) R(A2) 和 N ( A 2 ) N(\mathbf{A}^2) N(A2) 的一组基。从而直接计算可得,
X = ( − 8 12 8 ) , Y = ( − 1 0 1 0 0 1 ) , \left.\mathbf{X}=\left(\begin{array}{rr}-8\\12\\8\end{array}\right.\right),\quad\mathbf{Y}=\left(\begin{array}{rr}-1&0\\1&0\\0&1\end{array}\right), X= −8128 ,Y= −110001 ,
可得
Q = ( − 8 − 1 0 12 1 0 8 0 1 ) \left.\mathbf{Q}=\left(\begin{array}{rrr}-8&-1&0\\12&1&0\\8&0&1\end{array}\right.\right) Q= −8128−110001
所以
Q − 1 A Q = ( 1 4 1 4 0 − 3 − 2 0 − 2 − 2 1 ) ( − 2 0 − 4 4 2 4 3 2 2 ) ( − 8 − 1 0 12 1 0 8 0 1 ) = ( 2 0 0 0 − 2 4 0 − 1 2 ) \left.\mathbf{Q}^{-1}\mathbf{A}\mathbf{Q}=\left(\begin{array}{rrr}\frac{1}{4}&\frac{1}{4}&0\\-3&-2&0\\-2&-2&1\end{array}\right.\right)\left(\begin{array}{rrr}-2&0&-4\\4&2&4\\3&2&2\end{array}\right)\left(\begin{array}{rrrr}-8&-1&0\\12&1&0\\8&0&1\end{array}\right)=\left(\begin{array}{rrr}2&0&0\\0&-2&4\\0&-1&2\end{array}\right) Q−1AQ= 41−3−241−2−2001 −243022−442 −8128−110001 = 2000−2−1042
因为 Q − 1 A Q = ( C 0 0 N ) , C = ( 2 ) , N = ( − 2 4 − 1 2 ) \left.\mathbf{Q}^{-1}\mathbf{AQ}=\left(\begin{array}{ll}\mathbf{C}&\mathbf{0}\\\mathbf{0}&\mathbf{N}\end{array}\right.\right),\left.\mathbf{C}=(2),\mathbf{N}=\left(\begin{array}{cc}-2&4\\-1&2\end{array}\right.\right) Q−1AQ=(C00N),C=(2),N=(−2−142)
所以
相关文章:

核—幂零分解
若向量空间 V \mathcal V V存在子空间 X \mathcal X X与 Y \mathcal Y Y,当 X Y V X ∩ Y 0 \mathcal {X\text{}Y\text{}V}\\ \mathcal {X}\cap \mathcal {Y}0 XYVX∩Y0 时称子空间 X \mathcal X X与 Y \mathcal Y Y是完备的,其中记为 X ⊕ Y V \ma…...

轻松掌控财务,分析账户花销,明细记录支出情况
随着科技的发展,我们的生活变得越来越智能化。然而,对于许多忙碌的现代人来说,管理财务可能是一件令人头疼的事情。复杂的账单、花销、收入,这些可能会让你感到无从下手。但现在,我们有一个全新的解决方案——一款全新…...

竞赛 题目:基于机器视觉opencv的手势检测 手势识别 算法 - 深度学习 卷积神经网络 opencv python
文章目录 1 简介2 传统机器视觉的手势检测2.1 轮廓检测法2.2 算法结果2.3 整体代码实现2.3.1 算法流程 3 深度学习方法做手势识别3.1 经典的卷积神经网络3.2 YOLO系列3.3 SSD3.4 实现步骤3.4.1 数据集3.4.2 图像预处理3.4.3 构建卷积神经网络结构3.4.4 实验训练过程及结果 3.5 …...

11. Spring源码篇之实例化前的后置处理器
简介 spring在创建Bean的过程中,提供了很多个生命周期,实例化前就是比较早的一个生命周期,顾名思义就是在Bean被实例化之前的处理,这个时候还没实例化,只能拿到该Bean的Class对象,如果在这个时候直接返回一…...

Python-Python高阶技巧:HTTP协议、静态Web服务器程序开发、循环接收客户端的连接请求
版本说明 当前版本号[20231114]。 版本修改说明20231114初版 目录 文章目录 版本说明目录HTTP协议1、网址1.1 网址的概念1.2 URL的组成1.3 知识要点 2、HTTP协议的介绍2.1 HTTP协议的概念及作用2.2 HTTP协议的概念及作用2.3 浏览器访问Web服务器的过程 3、HTTP请求报文3.1 H…...

P1304 哥德巴赫猜想
题目描述 输入一个偶数 N,验证 4∼N 所有偶数是否符合哥德巴赫猜想:任一大于 22 的偶数都可写成两个质数之和。如果一个数不止一种分法,则输出第一个加数相比其他分法最小的方案。例如 1010,10=3+7=5+510=3+7=5+5,则 10=5+510=5+5 是错误答案。 输入格式 第一行输入一个…...
)
CSDN每日一题学习训练——Python版(搜索插入位置、最大子序和)
版本说明 当前版本号[20231118]。 版本修改说明20231118初版 目录 文章目录 版本说明目录搜索插入位置题目解题思路代码思路参考代码 最大子序和题目解题思路代码思路参考代码 搜索插入位置 题目 给定一个排序数组和一个目标值,在数组中找到目标值,…...

Java在物联网中的重要性
【点我-这里送书】 本人详解 作者:王文峰,参加过 CSDN 2020年度博客之星,《Java王大师王天师》 公众号:JAVA开发王大师,专注于天道酬勤的 Java 开发问题中国国学、传统文化和代码爱好者的程序人生,期待你的关注和支持!本人外号:神秘小峯 山峯 转载说明:务必注明来源(…...

动态规划解背包问题
题目 题解 def knapsac(W: int, N: int, wt: List[int], val: List[int]) -> int:# 定义状态动作价值函数: dp[i][j],对于前i个物品,当前背包容量为j,最大的可装载价值dp [[0 for j in range(W1)] for i in range(N1)]# 状态动作转移for…...

PCL内置点云类型
PCL内置了许多点云类型供我们使用,下面先介绍PLC内置的点云数据类型 PCL中的点云类型为PointT;至于为什么是PointT类型需要追随到原来的ros开发中去,因为PCL库也是从原来的ROS中剥离出来的;大家都一致的认为点云结构是离散的N维信…...

clickhouse数据结构和常用数据操作
背景, 大数据中查询用mysql时间太长, 使用clickhouse 速度快, 数据写入mysql后同步到clickhouse中 测试1千万数据模糊搜索 mysql 需要30-40秒 clickhouse 约 100ms 一 数据结构和存储引擎 1 查看clickhouse所有数据类型 select * from system.data_type_families; 2 …...
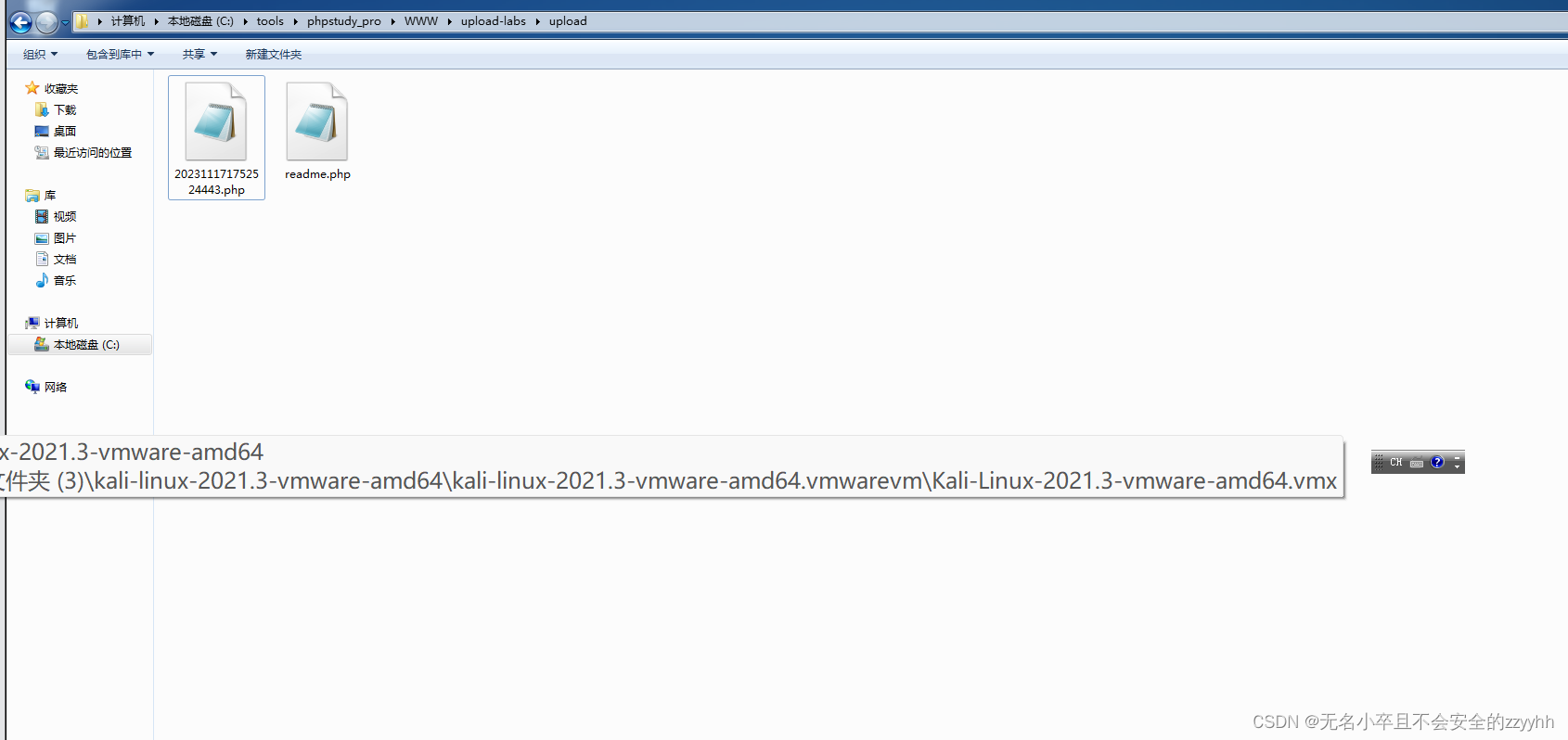
upload-labs关卡9(基于win特性data流绕过)通关思路
文章目录 前言一、靶场需要了解的知识1::$data是什么 二、靶场第九关通关思路1、看源码2、bp抓包修改后缀名3、检查是否成功上传 总结 前言 此文章只用于学习和反思巩固文件上传漏洞知识,禁止用于做非法攻击。注意靶场是可以练习的平台,不能随意去尚未授…...

C++过河卒问题
#include <iostream> #include <cstring> using namespace std;int board[20][20]; // 棋盘 int dp[20][20][20][20]; // 动态规划数组int main() {int x0, y0, x1, y1;cin >> x0 >> y0 >> x1 >> y1; // 输入卒的起点和终点memset(board,…...
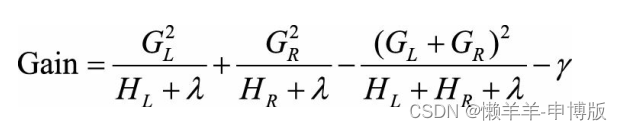
【机器学习12】集成学习
1 集成学习分类 1.1 Boosting 训练基分类器时采用串行的方式, 各个基分类器之间有依赖。每一层在训练的时候, 对前一层基分类器分错的样本, 给予更高的权重。 测试时, 根据各层分类器的结果的加权得到最终结果。 1.2 Bagging …...

nodeJs基础笔记
title: nodeJs基础笔记 date: 2023-11-18 22:33:54 tags: 1. Buffer 1. 概念 Buffer 是一个类似于数组的 对象 ,用于表示固定长度的字节序列。 Buffer 本质是一段内存空间,专门用来处理 二进制数据 。 2. 特点 Buffer 大小固定且无法调整Buffer 性能…...

Skywalking流程分析_9(JDK类库中增强流程)
前言 之前的文章详细介绍了关于非JDK类库的静态方法、构造方法、实例方法的增强拦截流程,本文会详细分析JDK类库中的类是如何被增强拦截的 回到最开始的SkyWalkingAgent#premain try {/** 里面有个重点逻辑 把一些类注入到Boostrap类加载器中 为了解决Bootstrap类…...

矩阵的QR分解
矩阵的QR分解 GramSchmidt 设存在 B { x 1 , x 2 , … , x n } \mathcal{B}\left\{\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right\} B{x1,x2,…,xn}在施密特正交化过程中 q 1 x 1 ∣ ∣ x 1 ∣ ∣ q_1\frac{x_1}{||x_1||} q1∣∣x1∣∣x1 q k …...

STL总结
STL vector 头文件<vector> 初始化,定义,定义长度,定义长度并且赋值,从数组中获取数据返回元素个数size()判断是否为空empty()返回第一个元素front()返回最后一个数back()删除最后一个数pop_back()插入push_back(x)清空clear()begin()end()使用s…...
资深测试总结,现在软件测试有未来吗?“你“的底气在哪里?
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、为什么会有 “…...

Scalable Exact Inference in Multi-Output Gaussian Processes
Orthogonal Instantaneous Linear Mixing Model TY are m-dimensional summaries,ILMM means ‘Instantaneous Linear Mixing Model’,OILMM means ‘Orthogonal Instantaneous Linear Mixing Model’ 辅助信息 作者未提供代码...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
