大数据HCIE成神之路之数学(3)——概率论
概率论
- 1.1 概率论内容介绍
- 1.1.1 概率论介绍
- 1.1.2 实验介绍
- 1.2 概率论内容实现
- 1.2.1 均值实现
- 1.2.2 方差实现
- 1.2.3 标准差实现
- 1.2.4 协方差实现
- 1.2.5 相关系数
- 1.2.6 二项分布实现
- 1.2.7 泊松分布实现
- 1.2.8 正态分布
- 1.2.9 指数分布
- 1.2.10 中心极限定理的验证
1.1 概率论内容介绍
1.1.1 概率论介绍
概率论是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的,在一定条件下必然发生某一结果的现象称为 决定性现象 。
概率论是用来描述不确定性的数学工具,很多数据挖掘中的算法都是通过描述样本的概率相关信息或推断来构建模型。
1.1.2 实验介绍
本章节主要实现概率与统计相关的知识点,主要用到的框架是 numpy 和 scipy 框架。
1.2 概率论内容实现
导入相应库:
import numpy as np
import scipy as sp
1.2.1 均值实现
数据准备:
ll = [[1,2,3,4,5,6],[3,4,5,6,7,8]]
代码输入:
np.mean(ll) #全部元素求均值
结果输出:
4.5
np.mean(ll,0) #按列求均值,0代表列向量
结果输出:
array([2., 3., 4., 5., 6., 7.])
np.mean(ll,1) #按行求均值,1表示行向量
结果输出:
array([3.5, 5.5])
1.2.2 方差实现
数据准备:
b=[1,3,5,6]
ll=[[1,2,3,4,5,6],[3,4,5,6,7,8]]
求方差(variance):
np.var(b)
结果输出:
3.6875
代码输入:
np.var(ll,1) #第二个参数为1,表示按行求方差
结果输出:
[2.91666667 2.91666667]
解释:按行求方差,所以可以将ll拆开来计算也是可以得到一样的结果的
aa = [1,2,3,4,5,6]
np.var(aa)
bb = [3,4,5,6,7,8]
np.var(bb)
得到的结果都是 2.9166666666666665 ,保留8位小数点,则是2.91666667。
自行实践:
ttt,ddd = np.var(ll,1)
print(ttt, ddd)
思考:为什么aa与bb的方差都是一样的?
方差的意义:方差反映了一组数据与其平均值的偏离程度。 通常用方差来衡量一组数据的稳定性,方差越大,波动性越大;方差越小,波动性越小,也就越稳定。很明显,aa的平均值是3.5,bb的平均值是5.5,两者与其平均值的偏离程度是一样的,所以两者的方差一样。
注意:平均值相同,并不代表着方差相同。如:
aaa=[0,5,9,14]
bbb=[5,6,8,9]
两者的平均值都是7,但是方差却不相同,凭直觉上说,很明显aaa的元素偏离7要大一些,所以,凭直觉也是可以知道aaa的方差要比bbb的更大一些。
1.2.3 标准差实现
数据准备:
ll=[[1,2,3,4,5,6],[3,4,5,6,7,8]]
代码输入:
np.std(ll)
结果输出:
1.9790570145063195
补充:标准差也称为均方差,标准差是方差的算术平方根。
思考:为什么有了方差还有有标准差?
其实简单一句话解释就是,让计算结果不要与其自身的元素相差太大(单位一致)。
比如:
aaa=[0,5,9,14]
np.var(aaa)
计算结果是 26.5 ,可以发现,经过一个平方后,其方差的值26.5与其自身的元素(0,5,9,14)其实相差比较大了,我们可以再开个方根回来,让其值于原来的元素不要相差那么大,保持数据的单位一致。实际上np.std(aaa)的计算结果是 5.1478150704935 。
尝试: aaa=[0,50,90,140] ,请计算方差与标准差。
参考解释:有了方差为什么需要标准差?
1.2.4 协方差实现
数据准备:
b=[1,3,5,6]
代码输入:
np.cov(b)
结果输出:
4.916666666666666
补充: 协方差 (Covariance)在概率论和统计学中用于衡量 两个变量 的总体误差。而 方差 是协方差的一种特殊情况,即当 两个变量是相同 的情况。
说明:
b=[5,5]
np.cov(b)
np.std(b)
输出结果是一样的!b=[5,5,5,5,5]也是一样的。
1.2.5 相关系数
数据准备:
vc=[1,2,39,0,8]
vb=[1,2,38,0,8]
利用函数实现:
np.corrcoef(vc,vb)
结果输出:
array([[1. , 0.99998623],[0.99998623, 1. ]])
解释:输出结果是一个2x2的NumPy数组,表示两个变量 vc 和 vb 之间的相关系数矩阵。相关系数矩阵是一个对称矩阵,其中对角线上的元素是各自变量与自身的相关系数,而非对角线上的元素是两个不同变量之间的相关系数。
-
1.0:对角线上的元素表示每个变量与自身的相关系数。由于变量与自身完全相关,所以相关系数为1.0。 -
0.99998623:非对角线上的元素表示两个不同变量之间的相关系数。在这种情况下,vc 和 vb 之间的相关系数非常接近1.0,约为0.99998623。这表明这两个变量之间存在着极强的正线性相关性。
相关系数矩阵的结果表明变量 vc 和 vb 之间具有非常强的正线性相关性,即当一个变量增加时,另一个变量也会增加,且变化趋势非常相似。相关系数接近1.0表示它们之间的线性关系非常密切。
补充:coordination(协调、配合、协作)、 coefficient(系数)
1.2.6 二项分布实现
服从二项分布的随机变量X表示在n次独立同分布的伯努利试验中成功的次数,其中每次试验的成功概率为p。
from scipy.stats import binom, norm, beta, expon
import numpy as np
import matplotlib.pyplot as plt#n,p对应二项式公式中的事件成功次数及其概率,size表示采样次数,使用二项分布的rvs()函数生成了一个包含10000个样本的随机样本数组
binom_sim = binom.rvs(n=10, p=0.3, size=10000)
print('Data:',binom_sim)
print('Mean: %g' % np.mean(binom_sim))
print('SD: %g' % np.std(binom_sim, ddof=1)) # 当ddof=0时,表示总体标准差,为1时,表示样本的标准差。
#生成直方图,x指定每个bin(箱子)分布的数据,对应x轴,binx是总共有几条条状图,density值密度,也就是每个条状图的占比例比,默认为1
plt.hist(binom_sim, bins=10, density=True)
plt.xlabel(('x'))
plt.ylabel('density')
plt.show()
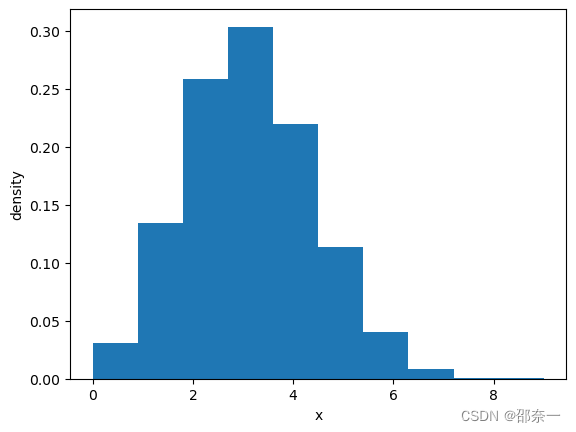
解释:二项分布(binom)、正态分布(norm)、贝塔分布(beta)和指数分布(expon),binom.rvs()函数生成的数据范围是从0到n之间的整数,其中n是二项分布的参数之一。类似于扔硬币,硬币有点特殊,扔10次,可能会有3次是人像面朝上(成功的概率)。所以,实际上扔下来,可能会有偏差的,请看下面的图像结果。
说明:旧版本是使用normed表示值密度,新版本是用density,直接替换即可,效果一样。
结果输出:
Data: [2 2 4 ... 1 4 2]
Mean: 2.9918
SD: 1.4365
二项分布图如下:
1.2.7 泊松分布实现
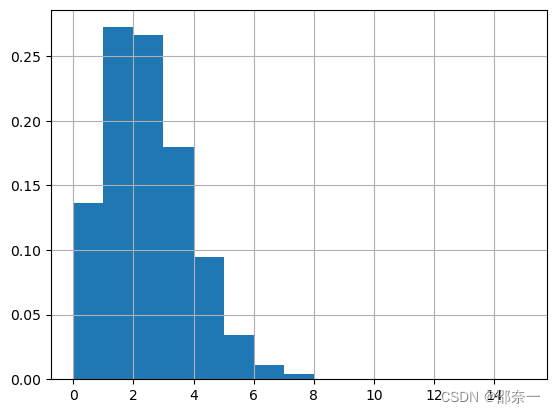
一个服从泊松分布的随机变量X,表示在具有比率参数λ的一段固定时间间隔内,事件发生的次数。参数λ告诉你该事件发生的比率。随机变量X的平均值和方差都是λ。
import numpy as np
import matplotlib.pyplot as plt#产生10000个符合lambda=2的泊松分布的数
X= np.random.poisson(lam=2, size=10000)
a = plt.hist(X, bins=15, density=True, range=[0, 15])#生成网格
plt.grid()
plt.show()
泊松分布图如下:
1.2.8 正态分布
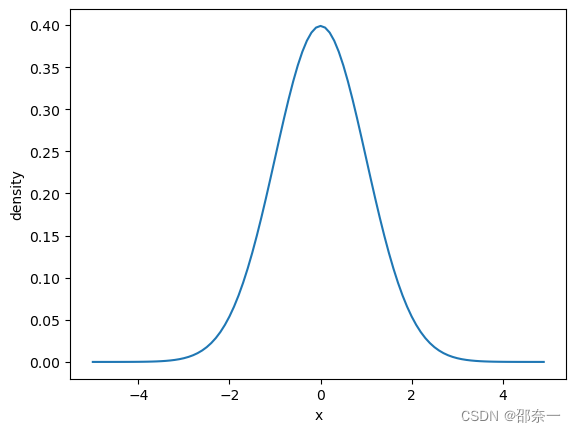
正态分布 是一种连续分布,其函数可以在实线上的任何地方取值。正态分布由两个参数描述:分布的平均值μ和标准差σ 。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as pltmu = 0
sigma = 1#分布采样点
x = np.arange(-5, 5, 0.1)
#生成符合mu,sigma的正态分布
y = norm.pdf(x, mu, sigma)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('density')
plt.show()
分布图如下:
1.2.9 指数分布
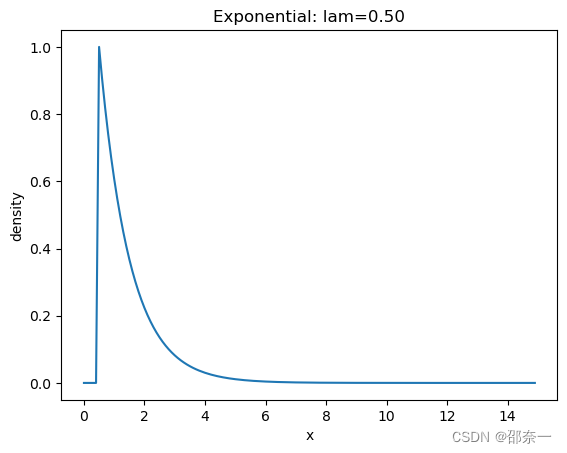
指数分布是一种连续概率分布,用于表示独立随机事件发生的时间间隔。比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔等。
from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as pltlam = 0.5
#分布采样点
x = np.arange(0, 15, 0.1)
#生成符合lambda为0.5的指数分布
y = expon.pdf(x, lam)
plt.plot(x, y)
plt.title('Exponential: lam=%.2f' % lam)
plt.xlabel('x')
plt.ylabel('density')
plt.show()
分布图如下:
1.2.10 中心极限定理的验证
中心极限定理证明了一系列相互独立的随机变量的和的极限分布为正态分布。即使总体本身不服从正态分布,只要样本组数足够多即可让中心极限定理发挥作用。此实验用于验证中心极限定理。
生成数据。假设观测一个人掷骰子,掷出1~6的概率都是相同的:1/6。掷了一万次。
import numpy as np
import matplotlib.pyplot as plt
#随机产生10000个范围为(1,6)的数
ramdon_data = np.random.randint(1,7,10000)
print(ramdon_data.mean())
print(ramdon_data.std())
输出结果:
3.4821
1.7102279351010499
生成直方图:
plt.figure()
plt.hist(ramdon_data,bins=6,facecolor='blue')
plt.xlabel('x')
plt.ylabel('n')
plt.show()
分布图如下:
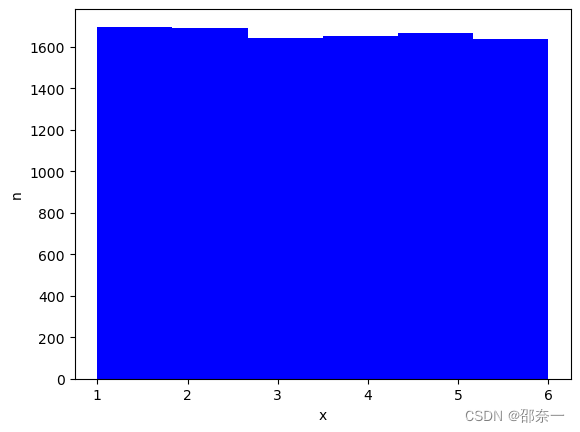
图解:投掷1万次,掷出1-6的次数相差无几。
随机抽取10个数据:
sample1 = []#从生成的1000个数中随机抽取10个
for i in range(1,10):# int(np.random.random()*len(ramdon_data))为随机生成范围为(0,10000)的整数sample1.append(ramdon_data[int(np.random.random()*len(ramdon_data))])sample1 = np.array(sample1)
print(sample1)
print(sample1.mean())
print(sample1.std())
输出如下:
[2 1 3 2 2 2 3 5 1]
2.3333333333333335
1.1547005383792515
随机抽取1000组数据,每组50个:
samples = []
samples_mean =[]
samples_std = []#从生成的1000个数中随机抽取1000组
for i in range(0,1000):sample = []#每组随机抽取50个数for j in range(0,50):sample.append(ramdon_data[int(np.random.random() * len(ramdon_data))])#将这50个数组成一个array放入samples列表中sample_ar = np.array(sample)samples.append(sample_ar)#保存每50个数的均值和标准差samples_mean.append(sample_ar.mean())
samples_std.append(sample_ar.std())
#samples_std_ar = np.array(samples_std)
#samples_mean_ar = np.array(samples_mean)
#print(samples_mean_ar)
生成直方图:
plt.figure()
#根据抽取的1000数据的均值,生成直方图,10个条形柱,柱的颜色为蓝色
plt.hist(samples_mean,bins=10,facecolor='blue')
plt.xlabel('x')
plt.ylabel('n')
plt.show()
分布图如下:
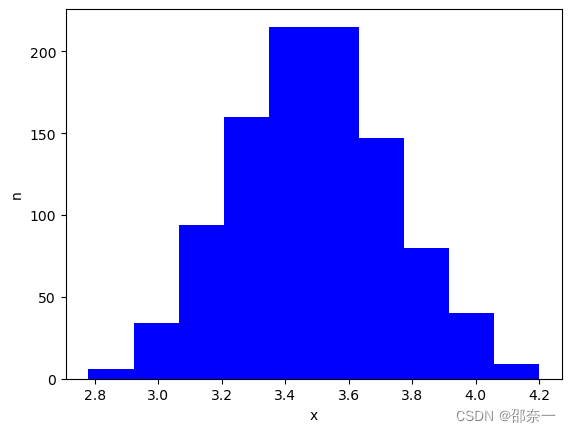
图解:相互独立的随机变量的和的极限分布为正态分布
相关文章:

大数据HCIE成神之路之数学(3)——概率论
概率论 1.1 概率论内容介绍1.1.1 概率论介绍1.1.2 实验介绍 1.2 概率论内容实现1.2.1 均值实现1.2.2 方差实现1.2.3 标准差实现1.2.4 协方差实现1.2.5 相关系数1.2.6 二项分布实现1.2.7 泊松分布实现1.2.8 正态分布1.2.9 指数分布1.2.10 中心极限定理的验证 1.1 概率论内容介绍…...
【论文解读】FFHQ-UV:用于3D面部重建的归一化面部UV纹理数据集
【论文解读】FFHQ-UV 论文地址:https://arxiv.org/pdf/2211.13874.pdf 0. 摘要 我们提出了一个大规模的面部UV纹理数据集,其中包含超过50,000张高质量的纹理UV贴图,这些贴图具有均匀的照明、中性的表情和清洁的面部区域,这些都是…...
)
simple foc 移植odriver foc的 anti-cogging(抗齿槽算法)
文章目录 ESP32 simple foc 移植odriver anti-cogging.1.硬件,在淘宝买的。esp32 simple foc(最新). 下电阻三采样。2. 效果,见视频https://www.bilibili.com/video/BV1xg4y1X7Yr/?vd_source4fd70d693021f289fb2d339c6c0407193.代码添加(生成…...
基于深度学习的恶意软件检测
恶意软件是指恶意软件犯罪者用来感染个人计算机或整个组织的网络的软件。 它利用目标系统漏洞,例如可以被劫持的合法软件(例如浏览器或 Web 应用程序插件)中的错误。 恶意软件渗透可能会造成灾难性的后果,包括数据被盗、勒索或网…...
环境配置|GitHub——解决Github无法显示图片以及README无法显示图片
一、问题背景 最近在整理之前写过的实验、项目,打算把这些东西写成blog,并把工程文件整理上传到Github上。但在上传README文件的时候,发现github无法显示README中的图片,如下图所示: 在README中该图片路径为࿱…...
试用 12 -- 年终再总结)
AIGC(生成式AI)试用 12 -- 年终再总结
上次使用年终总结为题测试了CSDN创作助手和文心一言的表现,随着不断对总结给出更细节的提示。AIGC(生成式AI)试用 11 -- 年终总结-CSDN博客 总结年终总结生活/工作年终总结IT开发/运维年终总结 AIGC都能就新给出的主题修饰给出相应的关点&am…...

Linux下 tar 命令详解
一、tar 命令概述 Tar(Tape ARchive,磁带归档的缩写,LCTT 译注:最初设计用于将文件打包到磁带上,现在我们大都使用它来实现备份某个分区或者某些重要的目录)。 tar 是类 Unix 系统中广泛使用的命令&#x…...

SQL单表复杂查询where、group by、order by、limit
1.1SQL查询代码如下: select job as 工作类别,count(job) as 人数 from tb_emp where entrydate <2015-01-01 group by job having count(job) > 2 order by count(job) limit 1,1where entrydate <‘2015-01-01’ 表示查询日期小于2015-01-01的记录…...
安卓中轻量级数据存储方案分析探讨
轻量级数据存储功能通常用于保存应用的一些常用配置信息,并不适合需要存储大量数据和频繁改变数据的场景。应用的数据保存在文件中,这些文件可以持久化地存储在设备上。需要注意的是,应用访问的实例包含文件所有数据,这些数据会一…...

数据结构【DS】栈的应用
描述一下如何实现括号匹配? 初始时栈为空。 从左往右遍历算术表达式中的每个括号元素: ①当遍历到左括号时,将其压入栈顶。 ②当遍历到右括号时,将栈顶元素出栈,并判断出栈的左括号与当前遍历的右括号是否匹配&…...

大数据数仓建模基础理论【维度表、事实表、数仓分层及示例】
文章目录 什么是数仓仓库建模?ER 模型三范式 维度建模事实表事实表类型 维度表维度表类型 数仓分层ODS 源数据层ODS 层表示例 DWD 明细数据层DWD 层表示例 DIM 公共维度层DIM 层表示例 DWS 数据汇总层DWS 层表数据 ADS 数据应用层ADS 层接口示例 数仓分层的优势 什么…...
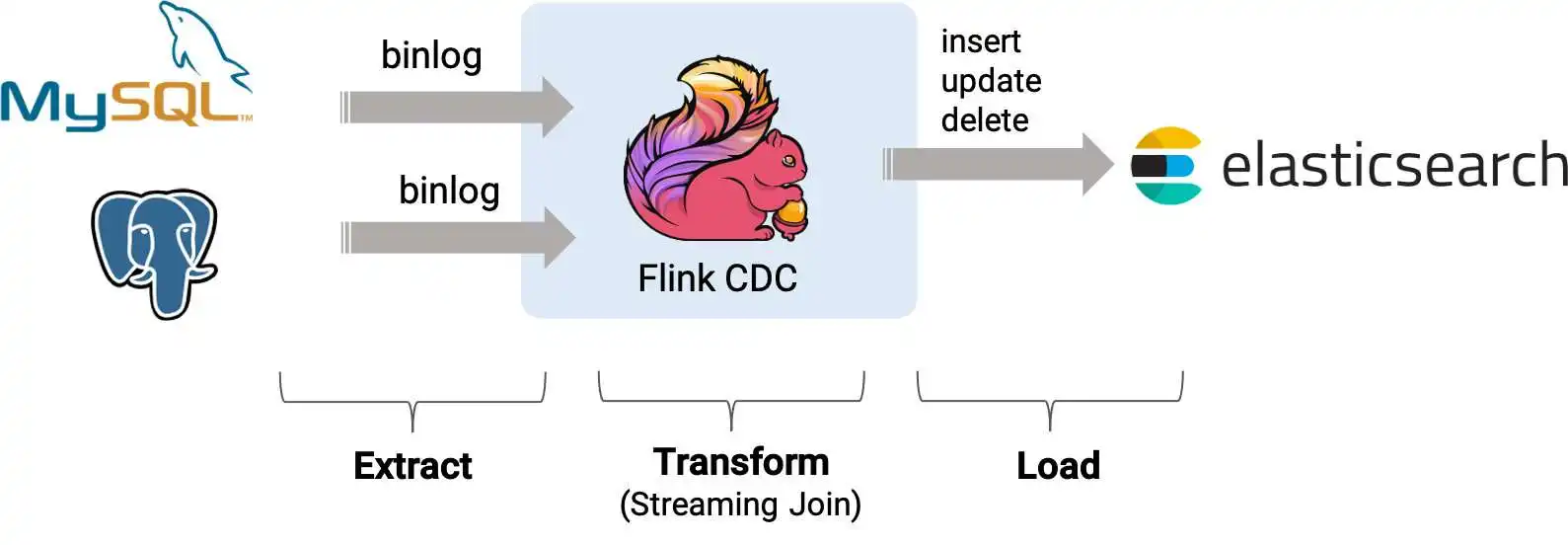
FlinkCDC数据实时同步Mysql到ES
考大家一个问题,如果想要把数据库的数据同步到别的地方,比如es,mongodb,大家会采用哪些方案呢? ::: 定时扫描同步? 实时日志同步? 定时同步是一个很好的方案,比较简单,但是如果对实时要求比较高的话,定…...

【Feign】 基于 Feign 远程调用、 自定义配置、性能优化、实现 Feign 最佳实践
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 SpringCloud MybatisPlus JVM 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Feign 一、 基于 Feign 远程调用1.1 RestTemplate方式…...
——基础入门3、基础入门4)
小迪安全笔记(3)——基础入门3、基础入门4
文章目录 一、抓包&封包&协议&APP&小程序&PC应用&web应用二、30余种加密编码进制&web&数据库&系统&代理 一、抓包&封包&协议&APP&小程序&PC应用&web应用 APP&小程序&PC抓包HTTP/S数据——Charles、F…...

SOME/IP 协议介绍(六)接口设计的兼容性规则
接口设计的兼容性规则(信息性) 对于所有序列化格式而言,向较新的服务接口的迁移有一定的限制。使用一组兼容性规则,SOME / IP允许服务接口的演进。可以以非破坏性的方式进行以下添加和增强: • 向服务中添加新方法 …...

吴恩达《机器学习》8-5->8-6:特征与直观理解I、样本与值观理解II
8.5、特征与直观理解I 一、神经网络的学习特性 神经网络通过学习可以得出自身的一系列特征。相对于普通的逻辑回归,在使用原始特征 x1,x2,...,xn 时受到一定的限制。虽然可以使用一些二项式项来组合这些特征,但仍然受到原始特征的限制。在神经网…...
『亚马逊云科技产品测评』活动征文|借助AWS EC2搭建服务器群组运维系统Zabbix+spug
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道。 本文基于以下软硬件工具: aws ec2 frp-0.52.3 zabbix 6…...

文件转换,简简单单,pdf转word,不要去找收费的了,自己学了之后免费转,之后就复制粘贴就ok了
先上一个链接pdf转word文件转换 接口层 PostMapping("pdfToWord")public String pdfToWord(RequestParam("file") MultipartFile file) throws IOException {String fileName FileExchangeUtil.pdfToWord(file.getInputStream(),file.getName());return…...

Jmeter——循环控制器中实现Counter计数器的次数重置
近期在使用Jmeter编写个辅助测试的脚本,用到了多个Loop Controller和Counter。 当时想的思路就是三个可变的数量值,使用循环实现;但第三个可变值的数量次数,是基于第二次循环中得到的结果才能确认最终次数,每次的结果…...

[创业之路-85]:IT创业成功老板的品质、创业失败老板的特征、成功领导者的品质、失败管理者的特征
目录 前言: 一、创业成功老板的品质 二、创业失败老板的特征 三、成功领导者的品质 四、失败管理者的特征 前言: 大多数创业或职场共事,都是基于某种人际关系或所谓的感情,这是大数的职场众生相,也是人情社会的中…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
