nn.KLDivLoss,nn.CrossEntropyLoss,nn.MSELoss,Focal_Loss
- KL loss:https://blog.csdn.net/qq_50001789/article/details/128974654
https://pytorch.org/docs/stable/nn.html
1. nn.L1Loss
1.1 公式
L1Loss: 计算预测 x和 目标y之间的平均绝对值误差MAE, 即L1损失:
l o s s = 1 n ∑ i = 1 , . . . n ∣ x i − y i ∣ loss=\frac{1}{n} \sum_{i=1,...n}|x_i-y_i| loss=n1i=1,...n∑∣xi−yi∣
1.2 语法
torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')
size_average与reduce已经被弃用,具体功能可由reduction替代reduction:指定损失输出的形式,有三种选择:none|mean|sum。none:损失不做任何处理,直接输出一个数组;mean:将得到的损失求平均值再输出,会输出一个数;sum:将得到的损失求和再输出,会输出一个数
注意:输入的x 与y 可以是任意维数的数组,但是二者形状必须一致
1.3 应用案例
对比reduction不同时,输出损失的差异
import torch.nn as nn
import torchx = torch.rand(10, dtype=torch.float)
y = torch.rand(10, dtype=torch.float)
L1_none = nn.L1Loss(reduction='none')
L1_mean = nn.L1Loss(reduction='mean')
L1_sum = nn.L1Loss(reduction='sum')
out_none = L1_none(x, y)
out_mean = L1_mean(x, y)
out_sum = L1_sum(x, y)
print(x)
print(y)
print(out_none)
print(out_mean)
print(out_sum)
2.nn.MSELoss
2.1 公式
MSELoss也叫L2 loss, 即计算预测x和目标y的平方误差损失。MSELoss的计算公式如下:
l o s s = 1 n ∑ i = 1 , . . n ( x i − y i ) 2 loss=\frac{1}{n} \sum_{i=1,..n}(x_i-y_i)^2 loss=n1i=1,..n∑(xi−yi)2
注:输入x 与y 可以是任意维数的数组,但是二者shape大小一致
2.2 语法
torch.nn.MSELoss(reduction = 'mean')
其中:
reduction:指定损失输出的形式,有三种选择:none|mean|sum。none:损失不做任何处理,直接输出一个数组;mean:将得到的损失求平均值再输出,会输出一个数;sum:将得到的损失求和再输出,会输出一个数
2.3 应用案例
对比reduction不同时,输出损失的差异
import torch.nn as nn
import torchx = torch.rand(10, dtype=torch.float)
y = torch.rand(10, dtype=torch.float)
mse_none = nn.MSELoss(reduction='none')
mse_mean = nn.MSELoss(reduction='mean')
mse_sum = nn.MSELoss(reduction='sum')
out_none = mse_none(x, y)
out_mean = mse_mean(x, y)
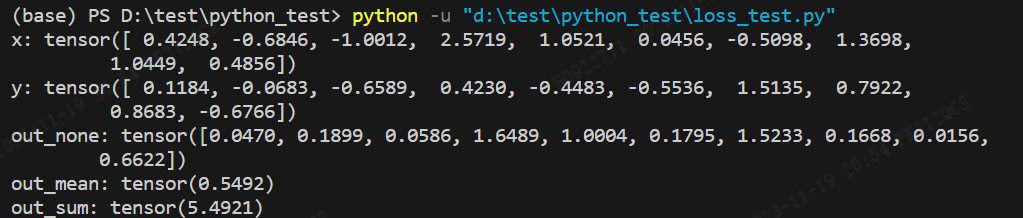
out_sum = mse_sum(x, y)print('x:',x)
print('y:',y)
print("out_none:",out_none)
print("out_mean:",out_mean)
print("out_sum:",out_sum)

3 nn.SmoothL1Loss
3.1 公式
SmoothL1Loss是结合L1 loss和L2 loss改进的,其数学定义如下:


如果绝对值误差低于 β \beta β, 则使用 L 2 L2 L2损失,,否则使用绝对值损失 L 1 L1 L1, ,此损失对异常值的敏感性低于 L 2 L2 L2 ,即当 x x x与 y y y相差过大时,该损失数值要小于 L 2 L2 L2损失,在某些情况下该损失可以防止梯度爆炸。
3.2 语法
torch.nn.SmoothL1Loss( reduction='mean', beta=1.0)
reduction:指定损失输出的形式,有三种选择:none|mean|sum。none:损失不做任何处理,直接输出一个数组;mean:将得到的损失求平均值再输出,会输出一个数;sum:将得到的损失求和再输出,会输出一个数beta:损失在 L 1 L1 L1和 L 2 L2 L2之间切换的阈值,默认beta=1.0
3.3 应用案例
import torch.nn as nn
import torch# reduction设为none便于逐元素对比损失值
loss_none = nn.SmoothL1Loss(reduction='none')
loss_sum = nn.SmoothL1Loss(reduction='sum')
loss_mean = nn.SmoothL1Loss(reduction='mean')
x = torch.randn(10)
y = torch.randn(10)
out_none = loss_none(x, y)
out_sum = loss_sum(x, y)
out_mean = loss_mean(x, y)
print('x:',x)
print('y:',y)
print("out_none:",out_none)
print("out_mean:",out_mean)
print("out_sum:",out_sum)
4. nn.CrossEntropyLoss
nn.CrossEntropyLoss 在pytorch中主要用于多分类问题的损失计算。
4.1 交叉熵定义
交叉熵主要是用来判定实际的输出与期望的输出的接近程度,也就是交叉熵的值越小,两个概率分布就越接近。
假设概率分布p为期望输出(target),概率分布q为实际输出(pred), H ( p , q ) H(p,q) H(p,q)为交叉熵, 则:


Pytorch中的CrossEntropyLoss()函数
Pytorch中计算的交叉熵并不是采用交叉熵定义的公式得到的,其中q为预测值,p为target值:

而是交叉熵的另外一种方式计算得到的:

Pytorch中CrossEntropyLoss()函数的主要是将log_softmax 和NLLLoss(最小化负对数似然函数)合并到一块得到的结果
CrossEntropyLoss()=log_softmax() + NLLLoss()

(1)首先对预测值pred进行softmax计算:其中softmax函数又称为归一化指数函数,它可以把一个多维向量压缩在(0,1)之间,并且它们的和为1

(2)然后对softmax计算的结果,再取log对数。(3)最后再利用NLLLoss() 计算CrossEntropyLoss, 其中NLLLoss() 的计算过程为:将经过log_softmax计算的结果与target相乘并求和,然后取反。
其中(1),(2)实现的是log_softmax计算,(3)实现的是NLLLoss(), 经过以上3步计算,得到最终的交叉熵损失的计算结果。
4.2 语法
torch.nn.CrossEntropyLoss(weight=None,size_average=None,ignore_index=-100,reduce=None,reduction='mean',label_smoothing=0.0)
- 最常用的参数为
reduction(str, optional),可设置其值为mean, sum, none,默认为 mean。该参数主要影响多个样本输入时,损失的综合方法。mean表示损失为多个样本的平均值,sum表示损失的和,none表示不综合。 weight: 可手动设置每个类别的权重,weight的数组大小和类别数需保持一致
4.3 应用案例
import torch.nn as nn
import torch
loss_func = nn.CrossEntropyLoss()
pre = torch.tensor([[0.8, 0.5, 0.2, 0.5]], dtype=torch.float)
tgt = torch.tensor([[1, 0, 0, 0]], dtype=torch.float)
print('----------------手动计算---------------------')
print("1.softmax")
print(torch.softmax(pre, dim=-1))
print("2.取对数")
print(torch.log(torch.softmax(pre, dim=-1)))
print("3.与真实值相乘")
print(-torch.sum(torch.mul(torch.log(torch.softmax(pre, dim=-1)), tgt), dim=-1))
print('-------------调用损失函数-----------------')
print(loss_func(pre, tgt))
print('----------------------------------------')
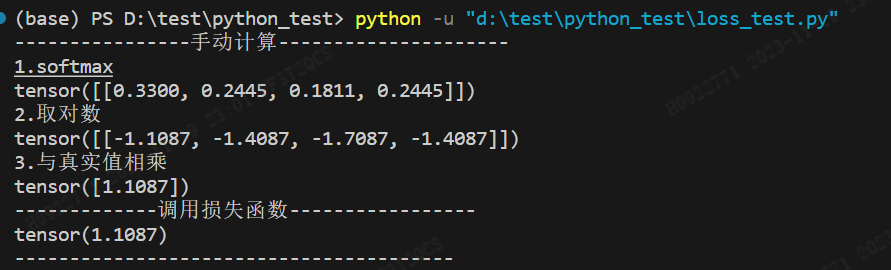
由此可见:
-
①交叉熵损失函数会自动对输入模型的预测值进行softmax。因此在
多分类问题中,如果使用nn.CrossEntropyLoss(),则预测模型的输出层无需添加softmax层。 -
②
nn.CrossEntropyLoss()=nn.LogSoftmax()+nn.NLLLoss().
nn.CrossEntropyLoss() 的target可以是one-hot格式,也可以直接输出类别,不需要进行one-hot处理,如下示例:
import torch
import torch.nn as nn
x_input=torch.randn(3,3)#随机生成输入
print('x_input:\n',x_input)
y_target=torch.tensor([1,2,0])#设置输出具体值 print('y_target\n',y_target)#计算输入softmax,此时可以看到每一行加到一起结果都是1
softmax_func=nn.Softmax(dim=1)
soft_output=softmax_func(x_input)
print('soft_output:\n',soft_output)#在softmax的基础上取log
log_output=torch.log(soft_output)
print('log_output:\n',log_output)#对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果,发现两者是一致的。
logsoftmax_func=nn.LogSoftmax(dim=1)
logsoftmax_output=logsoftmax_func(x_input)
print('logsoftmax_output:\n',logsoftmax_output)#pytorch中关于NLLLoss的默认参数配置为:reducetion=True、size_average=True
nllloss_func=nn.NLLLoss()
nlloss_output=nllloss_func(logsoftmax_output,y_target)
print('nlloss_output:\n',nlloss_output)#直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看与经过NLLLoss的计算是不是一样
crossentropyloss=nn.CrossEntropyLoss()
crossentropyloss_output=crossentropyloss(x_input,y_target)
print('crossentropyloss_output:\n',crossentropyloss_output)
- 其中pred为
x_input=torch.randn(3,3,对应的target为y_target=torch.tensor([1,2,0]), target并没有处理为one-hot格式,也可以正常计算结果的。
5. nn.BCELoss和nn.BCEWithLogitsLoss
相关文章:

nn.KLDivLoss,nn.CrossEntropyLoss,nn.MSELoss,Focal_Loss
KL loss:https://blog.csdn.net/qq_50001789/article/details/128974654 https://pytorch.org/docs/stable/nn.html 1. nn.L1Loss 1.1 公式 L1Loss: 计算预测 x和 目标y之间的平均绝对值误差MAE, 即L1损失: l o s s 1 n ∑ i 1 , . . . n ∣ x i…...
HTTP Error 500.31 - Failed to load ASP.NET Core runtime
在winserver服务器上部署net6应用后,访问接口得到以下提示: 原因是因为没有安装net6的运行时和环境,我们可以在windows自带的 “事件查看器” 查看原因。 可以直接根据给出的地址去官网下载sdk环境,安装即可 下载对应的net版本…...
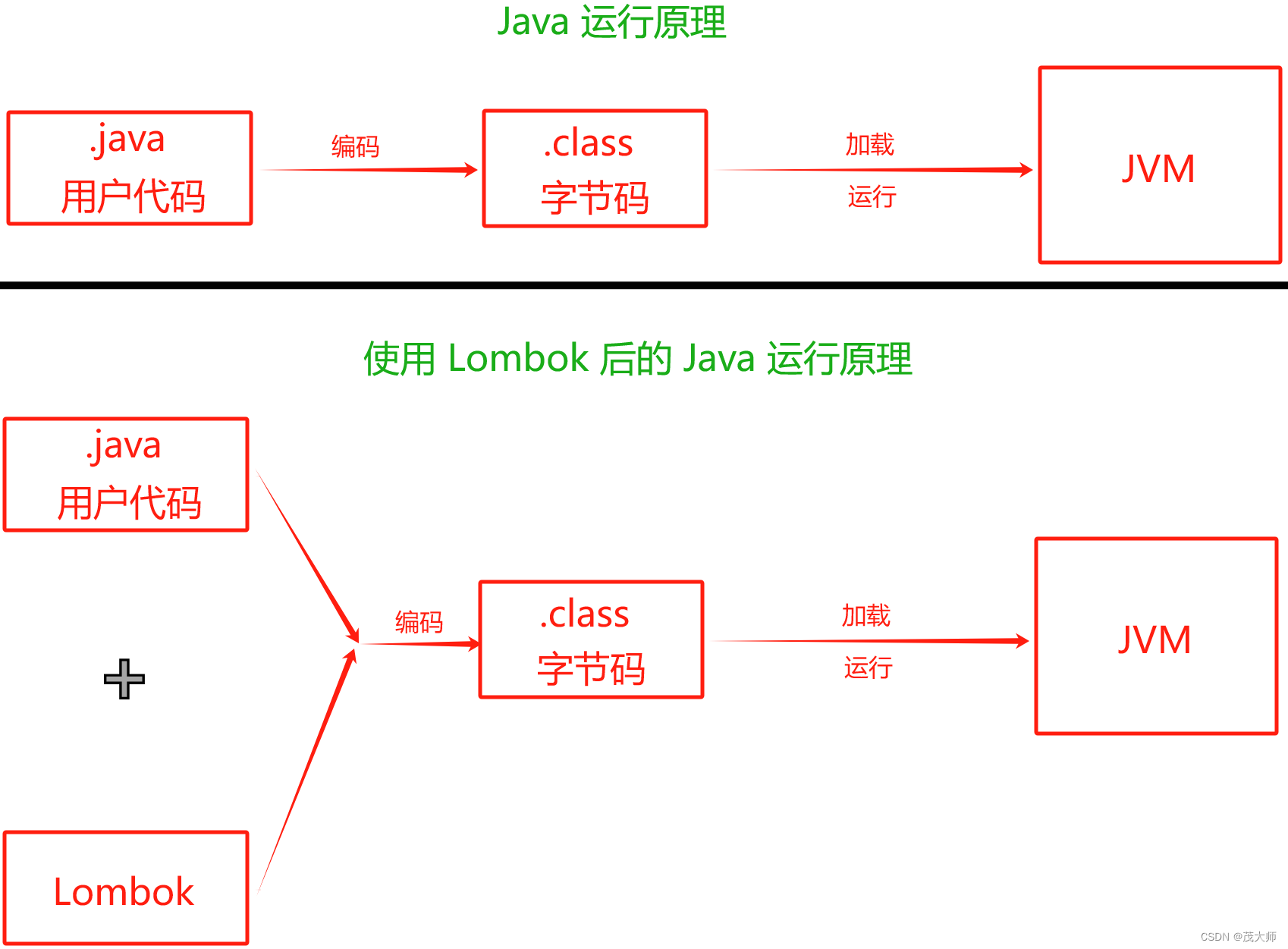
2023.11.17 关于 Spring Boot 日志文件
目录 日志文件作用 常见的日志框架说明 门面模式 日志的使用 日志的级别 六种级别 日志级别的设置 日志的持久化 使用 Lombok 输出日志 实现原理 普通打印和日志的区别 日志文件作用 记录 错误日志 和 警告日志(发现和定位问题)记录 用户登录…...

【框架整合】Redis限流方案
1、Redis实现限流方案的核心原理: redis实现限流的核心原理在于redis 的key 过期时间,当我们设置一个key到redis中时,会将key设置上过期时间,这里的实现是采用lua脚本来实现原子性的。2、准备 引入相关依赖 <dependency>…...
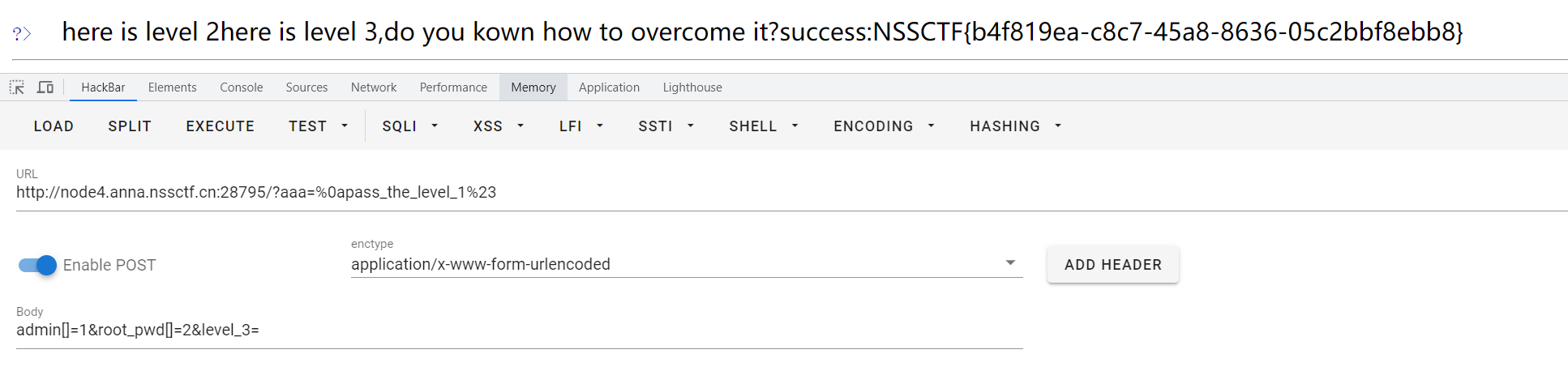
NSS [鹤城杯 2021]Middle magic
NSS [鹤城杯 2021]Middle magic 源码直接给了。 粗略一看,一共三个关卡 先看第一关: if(isset($_GET[aaa]) && strlen($_GET[aaa]) < 20){$aaa preg_replace(/^(.*)level(.*)$/, ${1}<!-- filtered -->${2}, $_GET[aaa]);if(preg_m…...
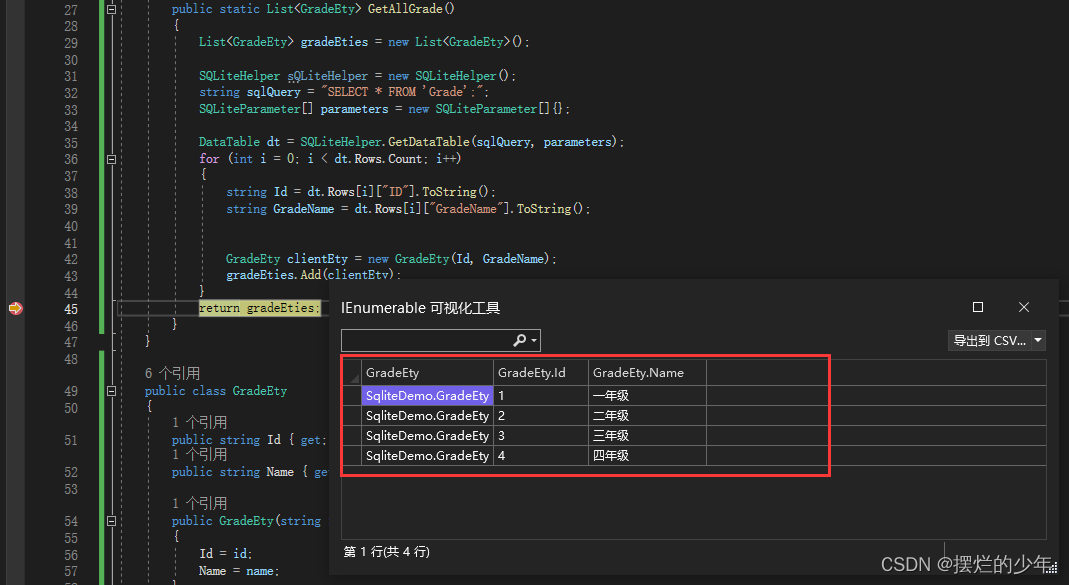
Sqlite安装配置及使用
一、下载SQLite Sqlite官网 我下载的是3370000版本:sqlite-dll-win64-x64-3370000.zip 和 sqlite-tools-win32-x86-3370000.zip 二、解压下载的两个压缩包 三、配置环境 四、检查是否安装配置成功 winR:输入cmd调出命令窗口,输入sqlite3后回车查看s…...
(点估计))
参数估计(一)(点估计)
文章目录 点估计和估计量的求法点估计概念矩估计法极大似然估计法 参考文献 参数估计是数理统计中重要的基本问题之一。通常,称参数的可容许值的全体为参数空间,并记为 Θ \Theta Θ。所谓参数估计就是由样本对总体分布所含的未知参数做出估计。另外&am…...
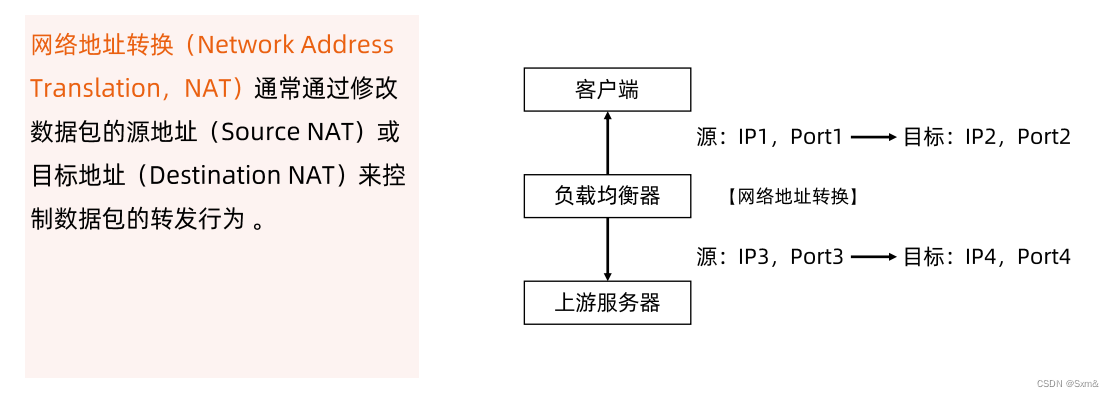
kubenetes-服务发现和负载均衡
一、服务发布 kubenetes把服务发布至集群内部或者外部,服务的三种不同类型: ClusterlPNodePortLoadBalancer ClusterIP是发布至集群内部的一个虚拟IP,通过负载均衡技术转发到不同的pod中。 NodePort解决的是集群外部访问的问题,用户可能不…...
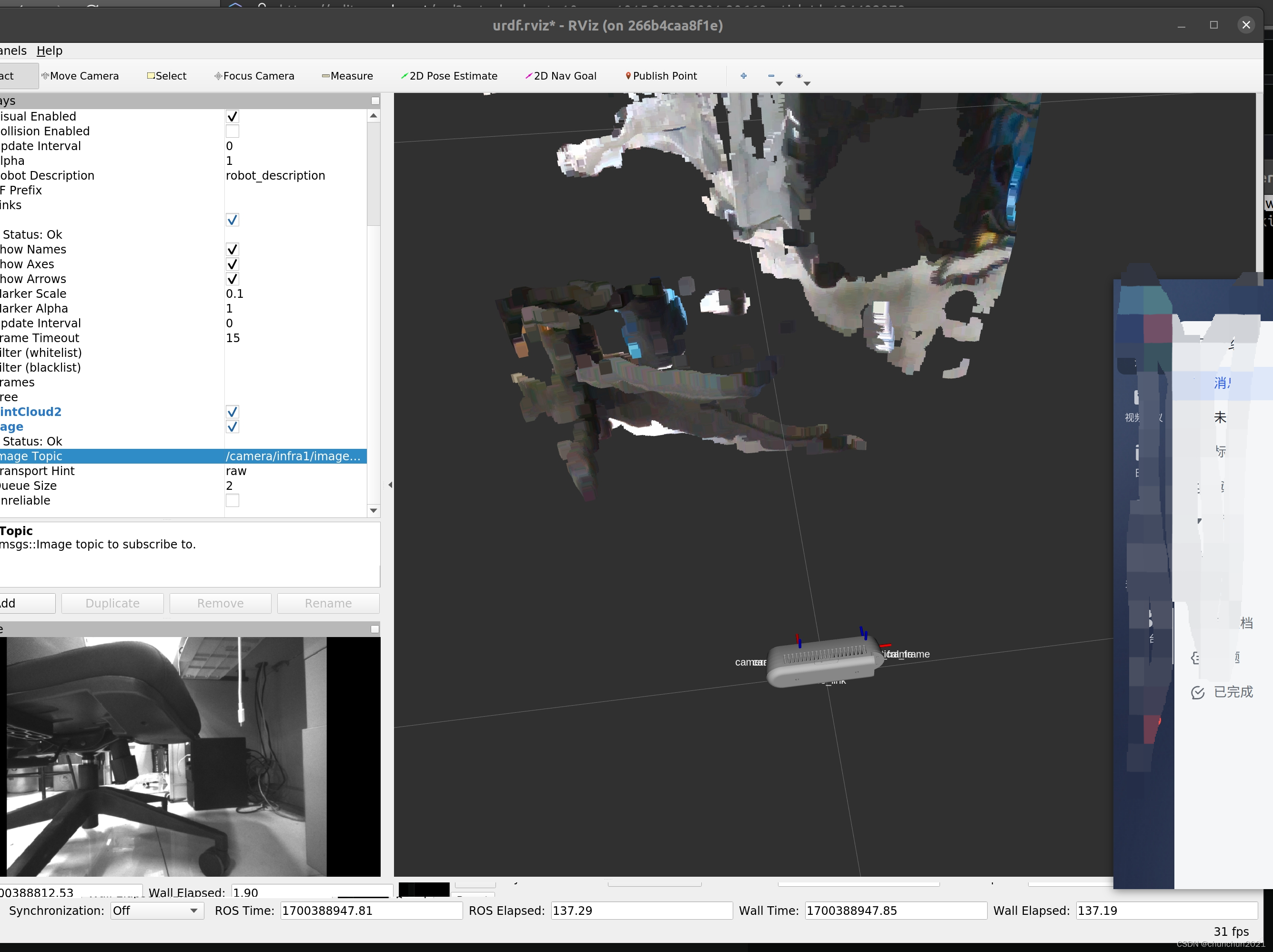
docker的基本使用以及使用Docker 运行D435i
1.一些基本的指令 1.1 容器 要查看正在运行的容器: sudo docker ps 查看所有的容器(包括停止状态的容器) sudo docker ps -a 重新命名容器 sudo docker rename <old_name> <new_name> <old_name> 替换为你的容器名称…...
如何看待人工智能行业发展
随着人工智能技术的飞速发展,这个领域的就业前景也日益广阔。人工智能在各行各业都有广泛的应用,包括医疗、金融、制造业、教育等。因此,对于想要追求高薪、高技能职业的人来说,学习人工智能是一个非常有前景的选择。 首先&#x…...

linux中实现自己的bash
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...

14 Go的类型转换
概述 在上一节的内容中,我们介绍了Go的错误处理,包括:errors包、返回错误、抛出异常、捕获异常等。在本节中,我们将介绍Go的类型转换。在Go语言中,类型转换是一种将一个值从一种类型转换为另一种类型的过程。类型转换主…...
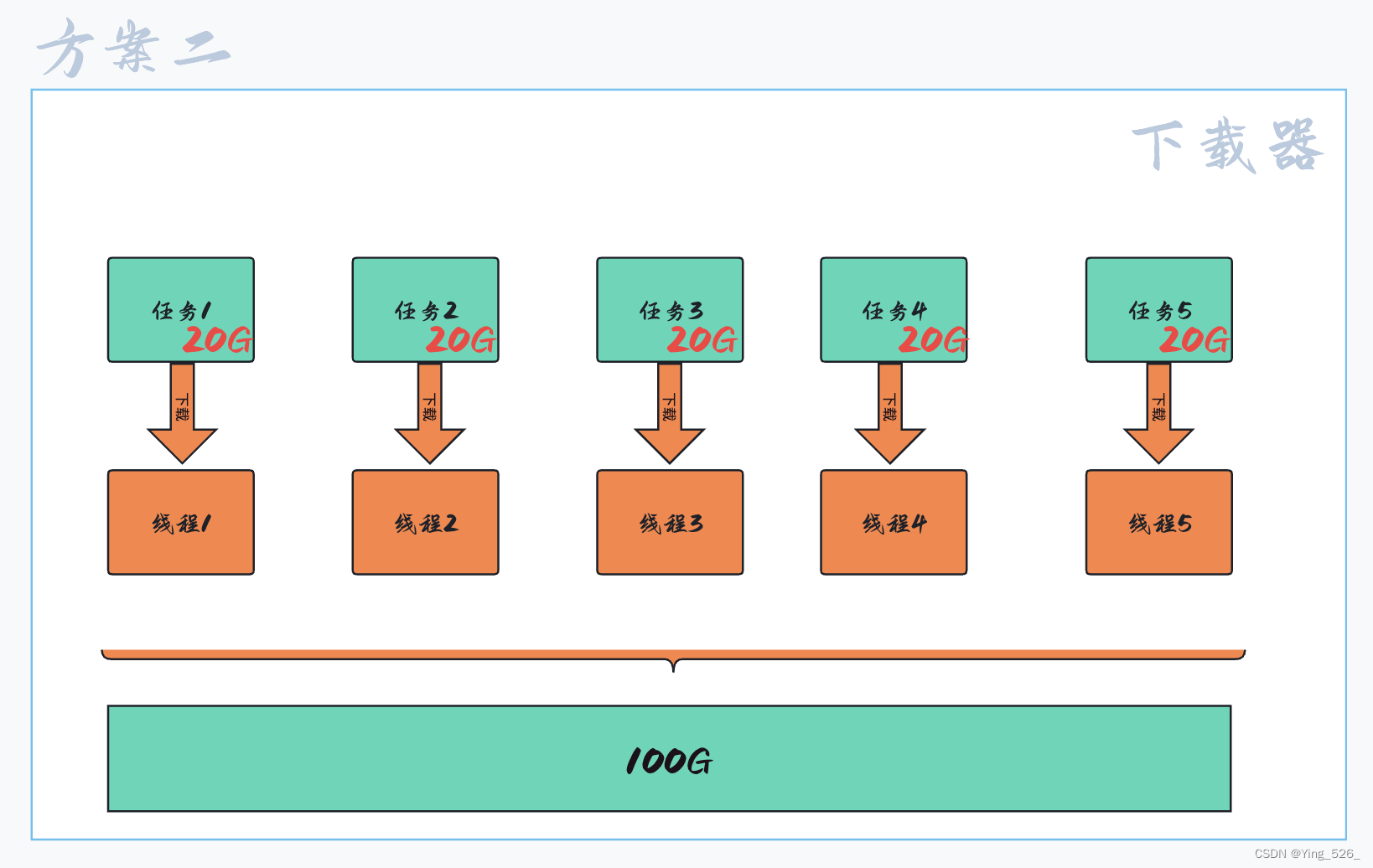
多线程概述
文章目录 线程是什么线程有什么作用线程和进程的区别多线程相较于进程优势 在Java这个圈子中,多进程用的并不多,因为进程是一个重量级操作,进程是资源分配的基本单位,申请资源是一个比较消耗时间的操作. 线程是什么 线程是一个独立的执行流,可以被独立调度到CPU上执行 线程是…...

AR贴纸特效SDK,无缝贴合的虚拟体验
增强现实(AR)技术已经成为了企业和个人开发者的新宠。它通过将虚拟元素与现实世界相结合,为用户提供了一种全新的交互体验。然而,如何将AR贴纸完美贴合在人脸的面部,同时支持多张人脸的检测和标点及特效添加࿰…...

Leetcode hot 100
双指针 283.移动零 class Solution { public:void moveZeroes(vector<int>& nums) {int cnt 0;for(vector<int>::iterator it nums.begin(); it ! nums.end(); ){if(*it 0) it nums.erase(it),cnt;else it;}while(cnt--){nums.push_back(0);}} }; 11.盛…...

分类预测 | Matlab实现基于SDAE堆叠去噪自编码器的数据分类预测
分类预测 | Matlab实现基于SDAE堆叠去噪自编码器的数据分类预测 目录 分类预测 | Matlab实现基于SDAE堆叠去噪自编码器的数据分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现基于SDAE堆叠去噪自编码器的数据分类预测(完整源码和数据) 2.多…...
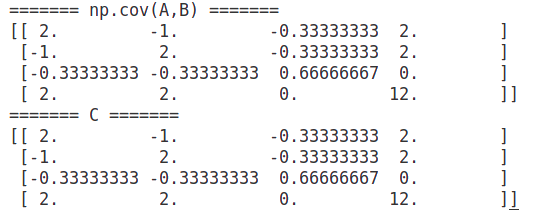
矩阵运算_矩阵的协方差矩阵/两个矩阵的协方差矩阵_求解详细步骤示例
1. 协方差矩阵定义 在统计学中,方差是用来度量单个随机变量的离散程度,而协方差则一般用来刻画两个随机变量的相似程度。 参考: 带你了解什么是Covariance Matrix协方差矩阵 - 知乎 2. 协方差矩阵计算过程 将输入数据A进行中心化处理得到A…...
——第108天:Pyecharts绘制多种炫酷词云图参数说明+代码实战)
100天精通Python(可视化篇)——第108天:Pyecharts绘制多种炫酷词云图参数说明+代码实战
文章目录 专栏导读一、词云图介绍1. 词云图是什么?2. 词云图应用场景?二、参数说明1. 导包2. add函数三、词云库实战1. 基础词云图2. 矩形词云图3. 三角形词云图4. 菱形词云图5. 自定义图片词云图书籍推荐专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本…...
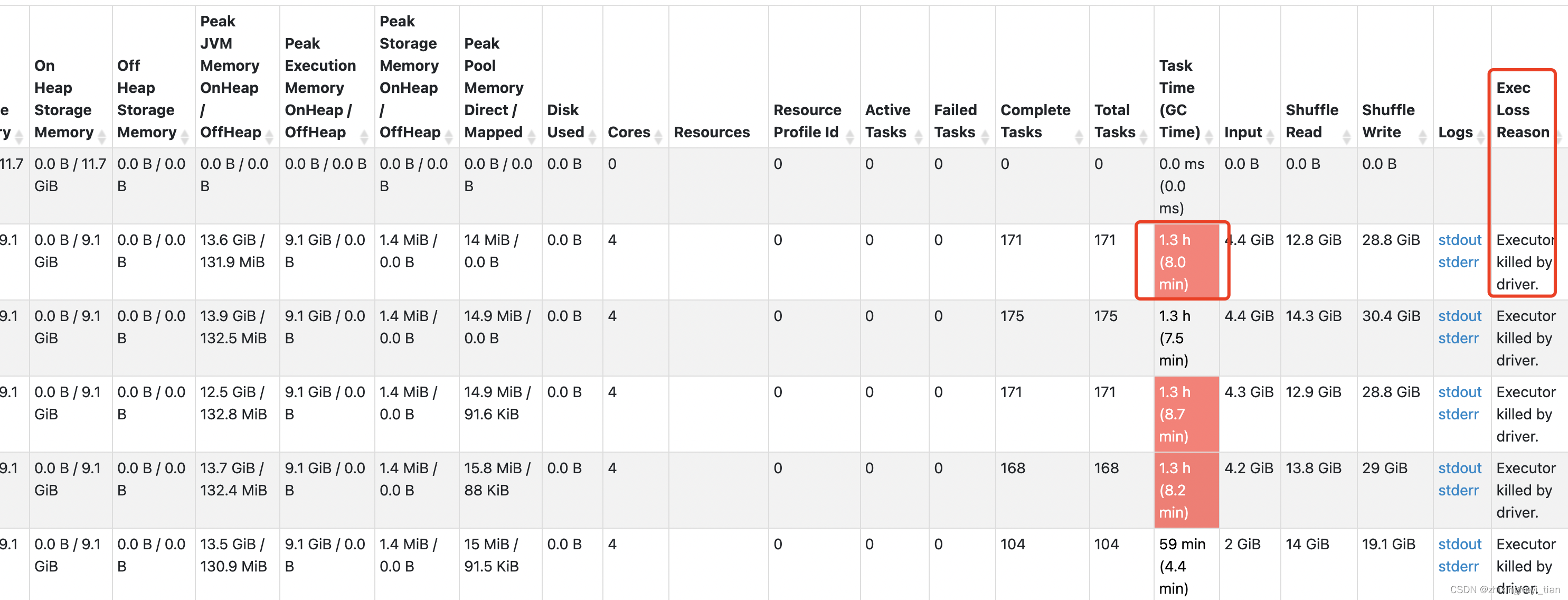
Spark 平障录
Profile Profile 是最重要的第一环。 利用好 spark UI 和 yarn container log分析业务代码,对其计算代价进行预判建设基准,进行对比,比如application id 进行对比,精确到 job DAG 环节 充分利用 UI Stage 页面 页头 summary&…...

基于一致性算法的微电网分布式控制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 本模型主要是基于一致性理论的自适应虚拟阻抗、二次电压补偿以及二次频率补偿,实现功率均分,保证电压以及频率稳定性。 一致性算法 分布式一致性控制主要分为两类:协调同…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
