Consistency Models 阅读笔记
简介
Diffusion models需要多步迭代采样才能生成一张图片,这导致生成速度很慢。一致性模型(Consistency models)的提出是为了加速生成过程。
Consistency models可以直接一步采样就生成图片,但是也允许进行多步采样来提高生成的质量。
Consistency models可以从预训练的扩散模型蒸馏得到,也可以作为独立的生成模型从头训练得到。
PF ODE
论文中考虑的PF ODE(Probability Flow Ordinary Differential Equation)形式如下:
d x t d t = − t s ϕ ( x t , t ) \frac{d \mathbf x_t}{d t} = -ts_\phi(\mathbf x_t, t) dtdxt=−tsϕ(xt,t)其中 s ϕ ( x t , t ) ≈ ∇ log p t ( x ) s_\phi(\mathbf x_t, t) \approx \nabla\log p_t(\mathbf x) sϕ(xt,t)≈∇logpt(x)是分数函数, t ∈ [ 0 , T ] t \in [0, T] t∈[0,T]。
从初始分布 x ^ T ∼ N ( 0 , T 2 I ) \mathbf{\hat x_T} \sim \mathcal N(\mathbf 0, T^2 \mathbf I) x^T∼N(0,T2I)中采样,然后逆向求解ODE,得到的 x ^ 0 \mathbf{\hat x_0} x^0是近似服从数据分布的样本。值得注意的是,为了保证数值稳定,在本文中用 x ^ ϵ \mathbf{\hat x_\epsilon} x^ϵ当做最后的近似样本, ϵ \epsilon ϵ是一个接近0的小正数。
一致性模型(Consistency models)
给定一个PF ODE(Probability Flow Ordinary Differential Equation) { x t } t ∈ [ ϵ , T ] \{\mathbf x_t\}_{t\in[\epsilon, T]} {xt}t∈[ϵ,T],一致性函数(consistency function)被定义为 f : ( x t , t ) → x ϵ f:(\mathbf x_t, t) \rightarrow \mathbf x_\epsilon f:(xt,t)→xϵ,其中 ϵ \epsilon ϵ是一个接近0的小正数,是ODE求解器停止的位置。一致性函数具有self-consistency性质,即对于PF ODE轨迹上的任意点输出都是一样的。一致性模型 f θ f_\theta fθ的是从数据中估计的一致性函数。
给一个训练好的一致性模型 f θ ( ⋅ , ⋅ ) f_\theta(\cdot, \cdot) fθ(⋅,⋅),可以通过一致性模型一步生成了结果:首先从初始分布中采样 x ^ T ∼ N ( 0 , T 2 I ) \mathbf{\hat x_T} \sim \mathcal N(\mathbf 0, T^2 \mathbf I) x^T∼N(0,T2I),然后用一致性模型计算 x ^ ϵ = f θ ( x ^ T , T ) \mathbf{\hat x_\epsilon} = f_\theta(\mathbf{\hat x_T}, T) x^ϵ=fθ(x^T,T)。也可以调用一致性模型多次生成更准确的结果,如Algorithm 1所示,迭代的去噪和添加噪声。

Consistency models的训练算法有两种,一种是从预训练的扩散模型蒸馏(Algorithm 2),一种是作为独立的生成模型从头训练(Algorithm 3)。

感觉一致性模型和EDM1有共同之处,在每一步中都想恢复出 x 0 \mathbf x_0 x0,但是一致性模型训练时优化的目标是self-consistency性质,通过self-consistency性质来在保证每一步中都能直接恢复出 x 0 \mathbf x_0 x0。
《Elucidating the design space of diffusion-based generative models》 ↩︎
相关文章:

Consistency Models 阅读笔记
简介 Diffusion models需要多步迭代采样才能生成一张图片,这导致生成速度很慢。一致性模型(Consistency models)的提出是为了加速生成过程。 Consistency models可以直接一步采样就生成图片,但是也允许进行多步采样来提高生成的质…...

杭电oj 2034 人见人爱A-B C语言
此处的c和a指向同一块内存空间,改变c就是改变a,反之亦然,此处是为了方便看这么写的,如果不想c和a指向同一空间请分别开辟空间(即不如此写camalloc) #include<stdio.h> #include<stdlib.h>int …...
)
springboot(ssm大学生成绩管理系统 成绩管理平台Java(codeLW)
springboot(ssm大学生成绩管理系统 成绩管理平台Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0&…...

SOME/IP 协议介绍(五)指南
指南(信息性) 选择传输协议 SOME/IP直接支持互联网上使用最广泛的两种传输协议:用户数据报协议(UDP)和传输控制协议(TCP)。UDP是一种非常简洁的传输协议,仅支持最重要的功能&#…...
Python调用企微机器人: 发送常用格式汇总
企微接口文档 发送应用消息 - 接口文档 - 企业微信开发者中心 发送格式 应用支持推送文本、图片、视频、文件、图文等类型。 ~~~以下列举常用格式 示例~~~ 1.发送文本 代码如下: def sendtxt_robotmsg(self):# 正式keywx_key "xx"wx_webhookurl htt…...

论文阅读——DiffusionDet
在目标检测上使用扩散模型 前向过程:真实框-->随机框 后向过程:随机框-->真实框 前向过程: 一般一张图片真实框的数目不同,填补到同一的N个框,填补方法可以是重复真实框,填补和图片大小一样的框&a…...

elmenetui表格二次封装包含查询框和分页
<!--dataList: 表格数据columnList: 表头字段 宽度minWidth使用slotName字段: 需要对列数据进行处理,不写prop字段,使用slotName字段btnText<String>: 按钮字段btnIcon<String>: 按钮的iconbtnEvent: 按钮事件btnType: 按钮类型getHeigh…...
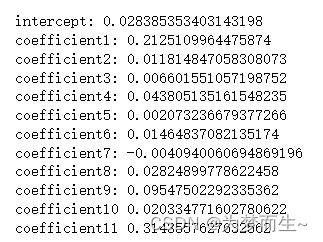
【机器学习Python实战】线性回归
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习python实战 欢迎订阅!后面的内容会越来越有意思~ ⭐内容说明:本专栏主要针对机器学习专栏的基础内容进行python的实现,部分…...

做外贸这么久,为什么一直做不好?
很多外贸业务员在开发客户过程中,总感觉自己做了很多事情,聊了很多客户,但却总是拿不到单子。 其实,这是由于缺乏对采购商心理的认识程度,没有换位思考,该做的事没做,不该做的事却忙得忘乎所以&…...
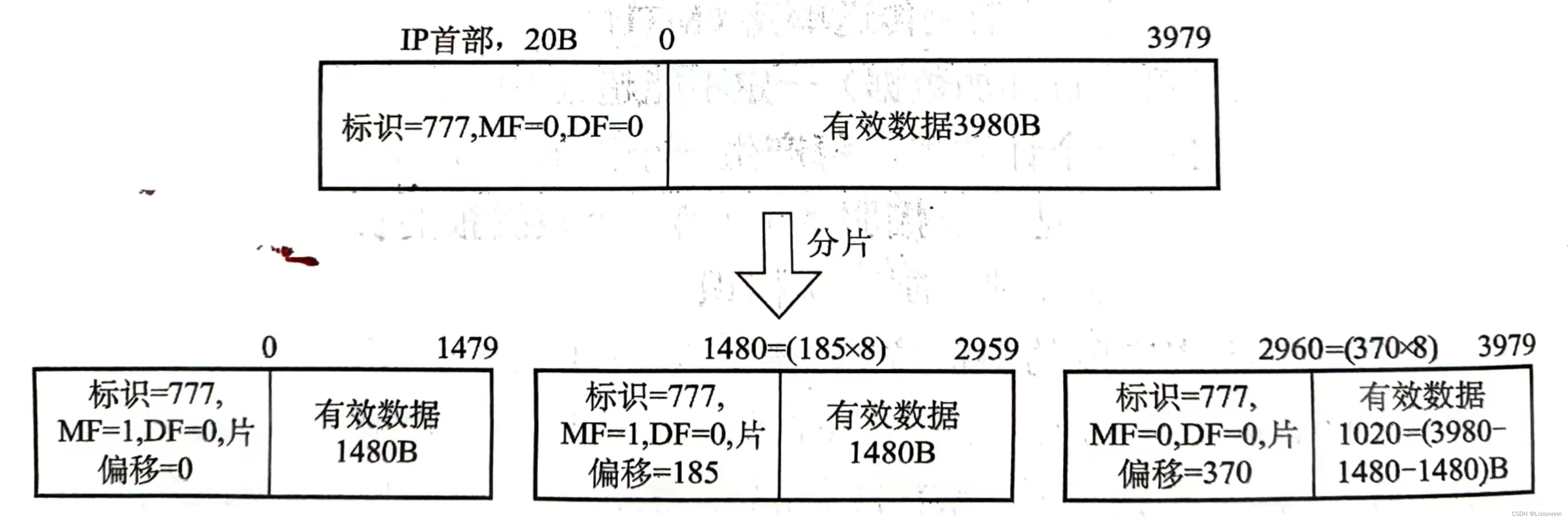
IPv4数据报格式
IPv4是IP协议的第四个版本(版本1-3和版本5都未曾使用过)IP地址不能反映任何有关主机位置的地理信息以前还有个逆地址解析协议RAPR(Reverse APR),它的作用是使只知道自己MAC地址的主机能通过RAPR找到其IP地址,而现在的DHCP(Dynamic Host Configuration Pr…...
搭建网关服务器实现DHCP自动分配、HTTP服务和免密登录
目录 一. 实验要求 二. 实验准备 三. 实验过程 1. 网关服务器新建网卡并改为仅主机模式 2. 修改新建网卡IP配置文件并重启服务 3. 搭建网关服务器的dhcp服务 4. 修改server2网卡配置文件重启服务并效验 5. 设置主机1的网络连接为仅主机模式 6. 给server2和网关服务器之…...
【18年扬大真题】给定有m个整数的递增有序数组a和有n个整数的递减有序数组b,将a数组和b数组归并为递增有序的数组c
【18年扬大真题】 给定有m个整数的递增有序数组a和有n个整数的递减有序数组b, 将a数组和b数组归并为递增有序的数组c。 void Merge(int arr[],int m ,int brr[],int n,int crr[]) {int i 0;int j n-1;int k 0;while(i < m&&j > 0) {if (arr[i] &l…...

图片叠加_图片压缩
图片叠加 try {/* 1 读取第一张图片*/File fileOne new File("1.png");BufferedImage imageFirst ImageIO.read(fileOne);/* 2读取第二张图片 */File fileTwo new File("2.png");BufferedImage imageSecond ImageIO.read(fileTwo);//创建一个最底层画…...
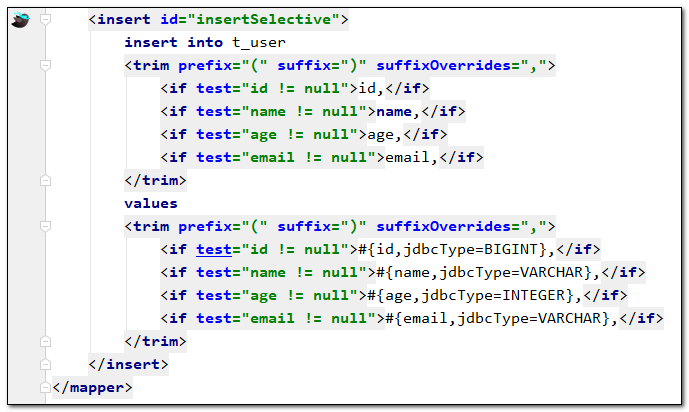
Mybatis-Plus《学习笔记 22版尚硅谷 》——感谢【尚硅谷】官方文档
Mybatis-Plus《学习笔记 22版尚硅谷 》 一、MyBatis-Plus1.简介2.特性3.支持数据库4.框架结构5.官方地址 二、入门案例1.开发环境2.建库建表3.创建工程4.配置编码5.测试查询 三、增删改查1.BaseMapper<T>2.调用Mapper层实现CRUD2.1 插入2.2 删除a、根据ID删除数据b、根据…...

git安装后报git: ‘remote-https‘ is not a git command. See ‘git --help‘.
1. 问题说明 使用的是linux系统,采用编译安装的方式进行安装,安装完成clone项目后提示“git: ‘remote-https’ is not a git command. See ‘git --help’.” 2. 问题解决 需要安装1个额外的库:libcurl4-openssl-de sudo apt-get install …...

场景交互与场景漫游-交运算与对象选取(8-1)
交运算与对象选取 在面对大规模的场景管理时,场景图形的交运算和图形对象的拾取变成了一项基本工作。OSG作为一个场景管理系统,自然也实现了场景图形的交运算,交运算主要封装在osgUtil 工具中在OSG中,osgUtil是一个非常强有力的工…...

Vue中动态Class实战
效果展示 需求 想实现一个假如有5个div块,默认都是灰色,鼠标悬浮到哪个div上,那个div就显示为黑色。 具体的实现业务逻辑可根据这个进行演变 设计 通过动态 class 类名来实现,实现鼠标悬浮到div时动态绑定class 版本 Vue 3.…...
B站短视频如何去水印?一键解析下载B站视频!
在浏览B站视频时,我们有时会遇到带有水印的场景。这些水印可能会干扰我们对视频内容的观看体验,特别是在全屏观看时。此外,当我们想要保存或分享这些视频时,水印也会成为一种障碍。因此,去除水印的需求就变得非常迫切。…...

最大子段和(分治法+动态规划法)
求最大子段和 此类问题通常是求数列中连续子段和的最大值,经典的股票问题就是考察的这个思想及拓展。 例题: AcWing:1054. 股票买卖 Leetcode:53. 最大子数组和 分治法O(nlogn) 此类问题时分适合采用分治思想,因为所有子区间 [ s t a r t …...
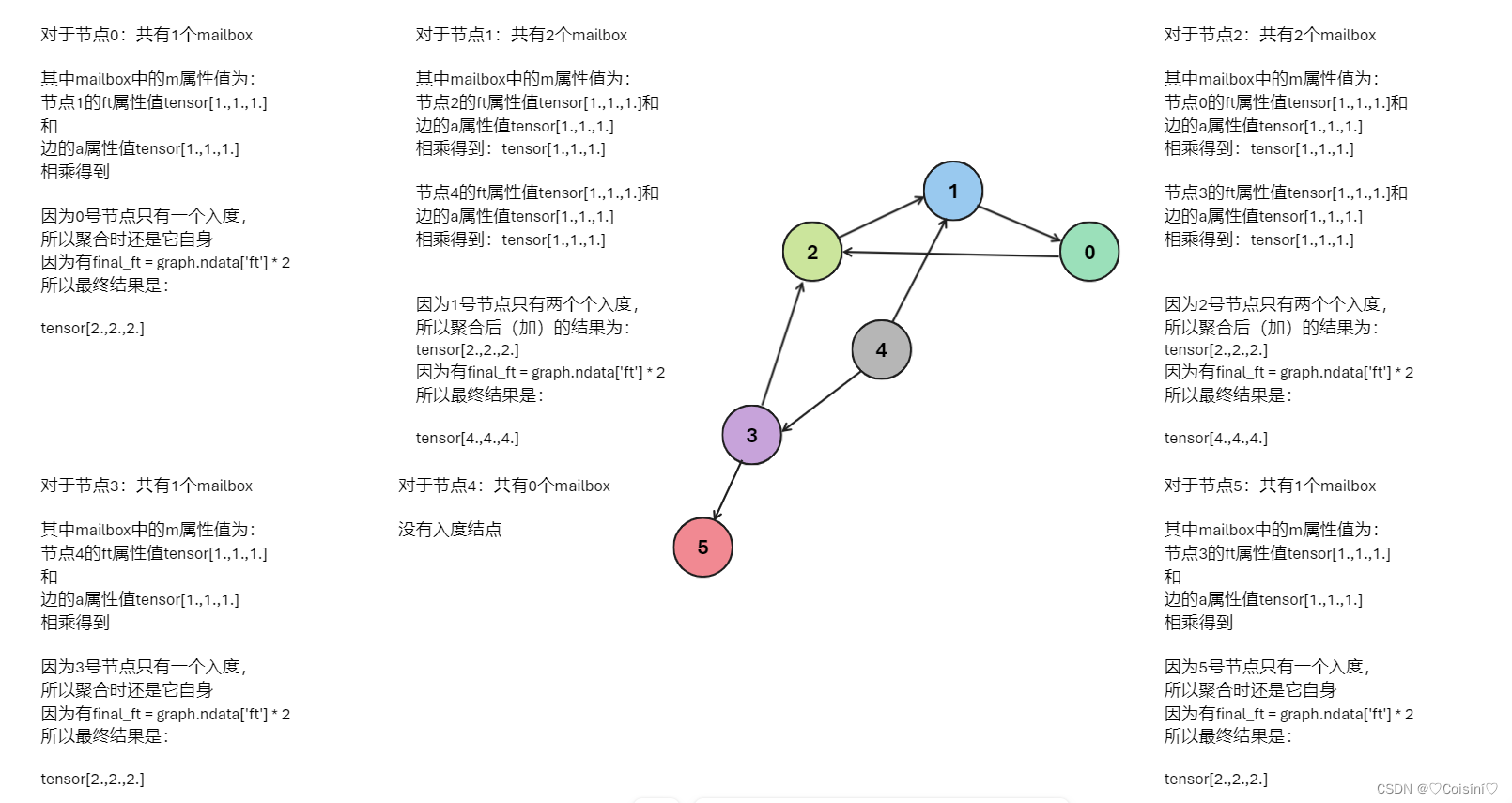
内置函数和消息传递API
消息传递范式 消息函数、聚合函数与更新函数 消息函数接受一个参数 edges,这是一个 EdgeBatch 的实例, 在消息传递时,它被DGL在内部生成以表示一批边。edges 有 src、 dst 和 data 共3个成员属性, 分别用于访问源节点、目标节点…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
