数电实验-----实现74LS153芯片扩展为8选1时间选择器以及应用(Quartus II )
目录
一、74LS153芯片介绍
管脚图
功能表
二、4选1选择器扩展为8选1选择器
1.扩展原理
2.电路图连接(Quartus II )
3.仿真结果
三、8选1选择器的应用
1.三变量表决器
2.奇偶校验电路
一、74LS153芯片介绍
74ls153芯片是属于四选一选择器的芯片。
74LS153是双4选1数据选择器,有选择输入端B和A,能有四种状态,选中输入4个数据中的其中一个数据,选择输入中L,H分别代表为L为低电平,H为高电平。选通输入可称为使能端,选通输入为高电平时,输出端Y为L低电平,选通为低电平时,输出Y为选择的数据输出。

管脚图
1G、2G是表示控制开关
A,B是表示地址选择器
1C0~1C3和2C0~2C3是输出口
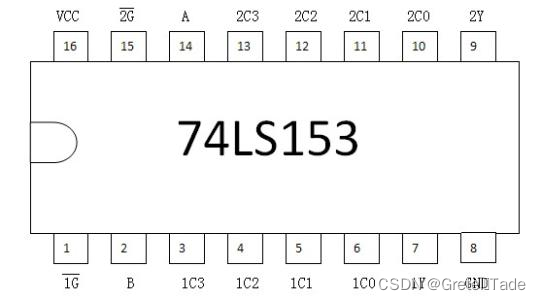
内部结构: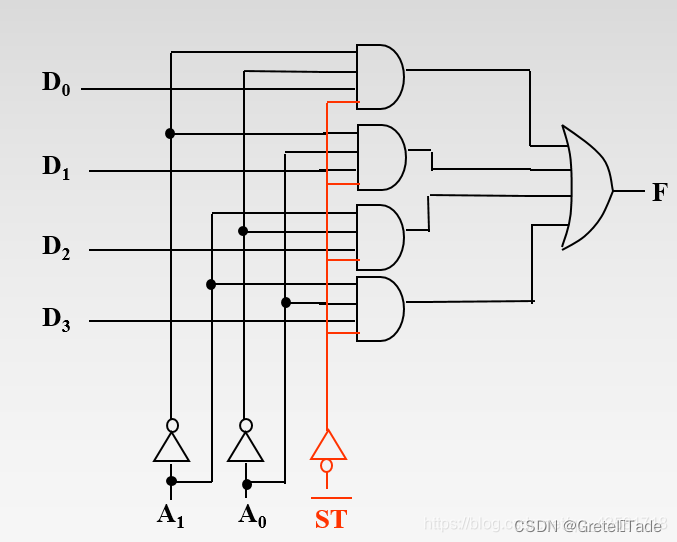
功能表
真值表:
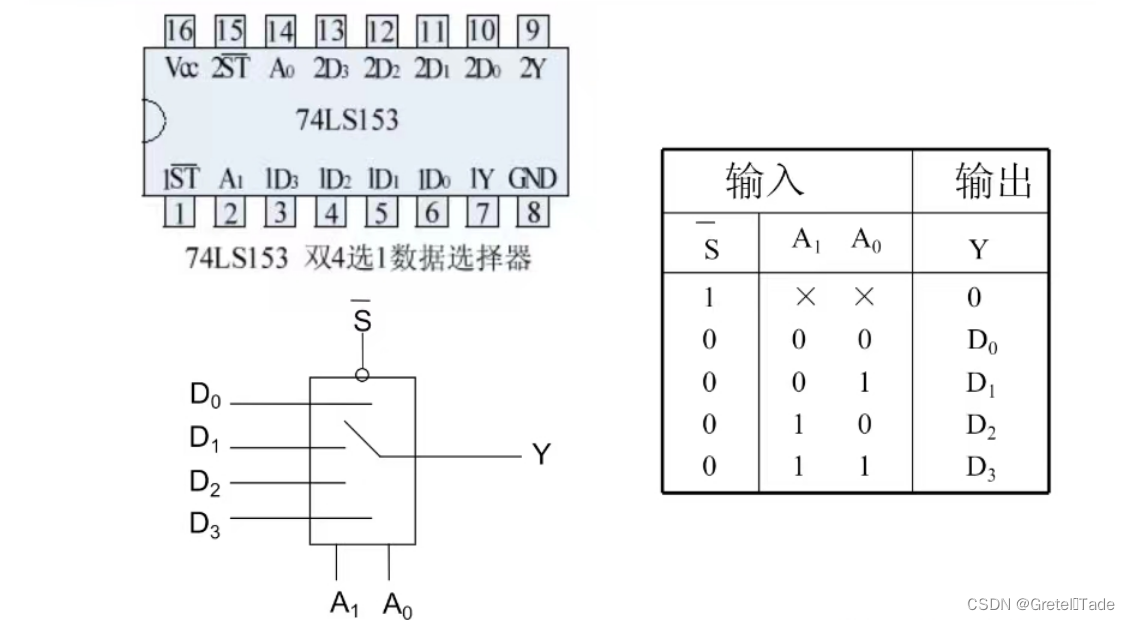
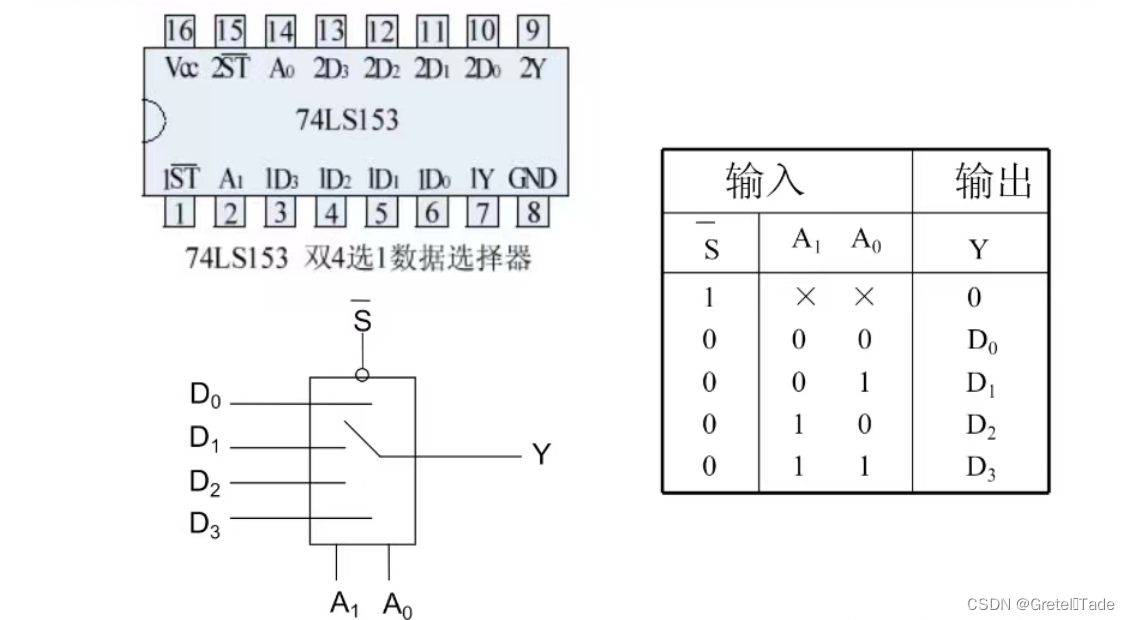
S是控制开关,当S为高电平的时候,表示不工作,反之就正常工作,A1和A0是地址选择器,选择相对应的地址输出。
二、4选1选择器扩展为8选1选择器
1.扩展原理
8选1选择器真值表:
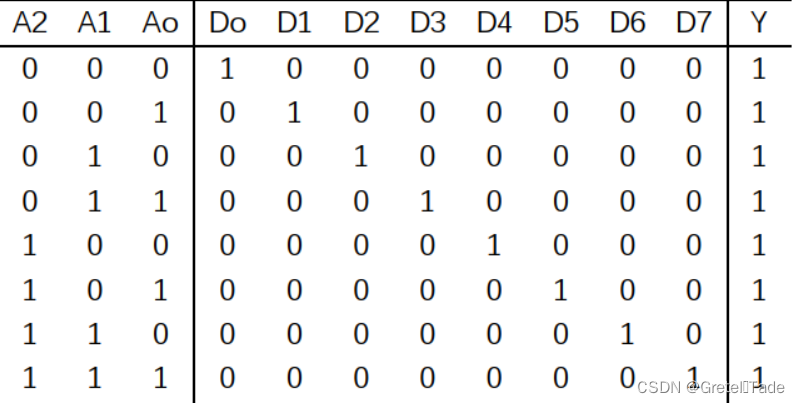
74ls153芯片有三个输入口,其中一个是选通开关S,其他两个是地址输出选择器A1 A0,这里我们就可以去通过这三个输入口作为8选1选择器的三个输入口。所以我们要用到两个4选1选择器来去实现8选1选择器的功能,通过两个4选1选择器交替工作实现输出的位选,我们让其中一个4选1选择器为高位选择器,另一个低位选择器,低位的选通开关取反接入到高位的开关,开关就作为A2。然后剩下的就是地址选择输出。下面看个示例:
比如,选通开关S、地址选择器A1、A0分别输入1 0 1,那么我们要输出就应该是高位的第2个,也就是输出D5即2D2这一条数据结果。那此时低位4选1选择器就不工作,所以输出的是0,也就只有高位的选择器在工作。
2.电路图连接(Quartus II )
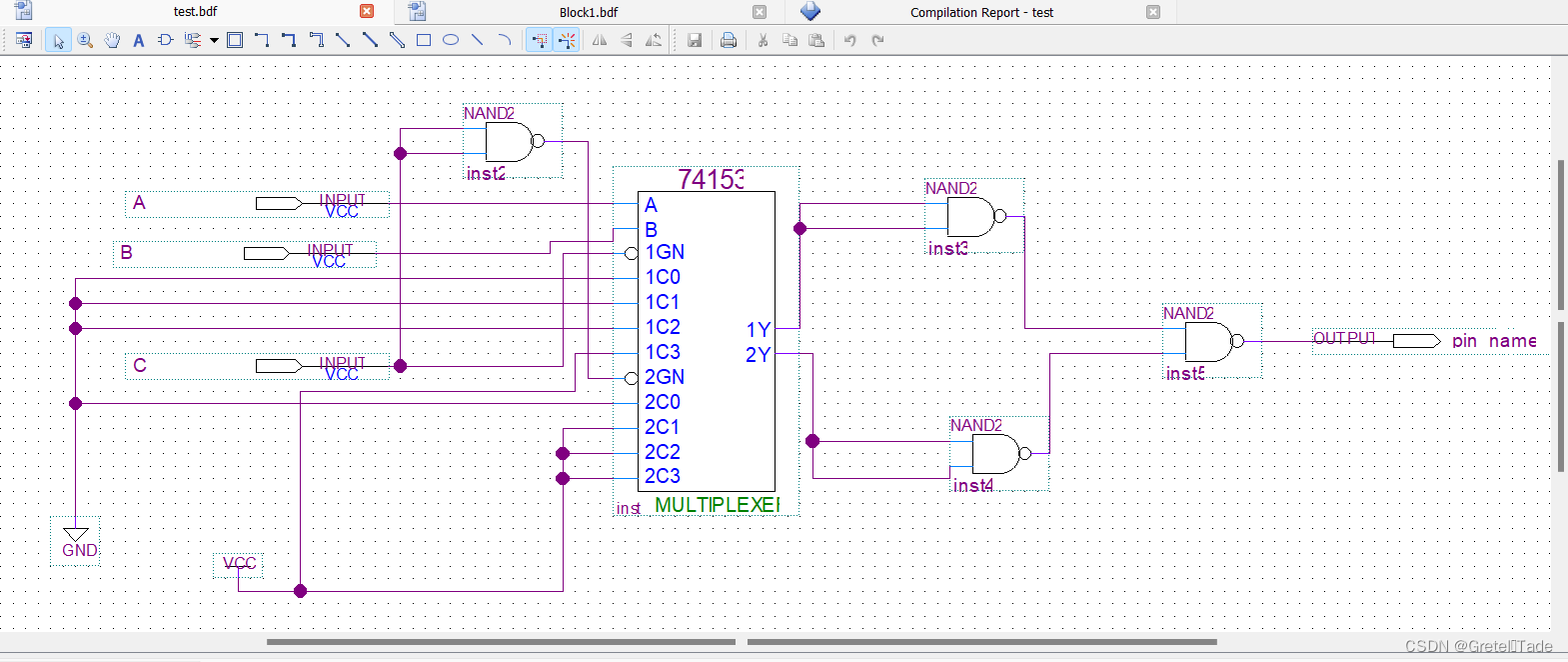
下面我们打开Quartus II,然后创建一个block文件,按照以下的图示连接,以下就是4选1选择器扩展为8选1选择器的电路图。
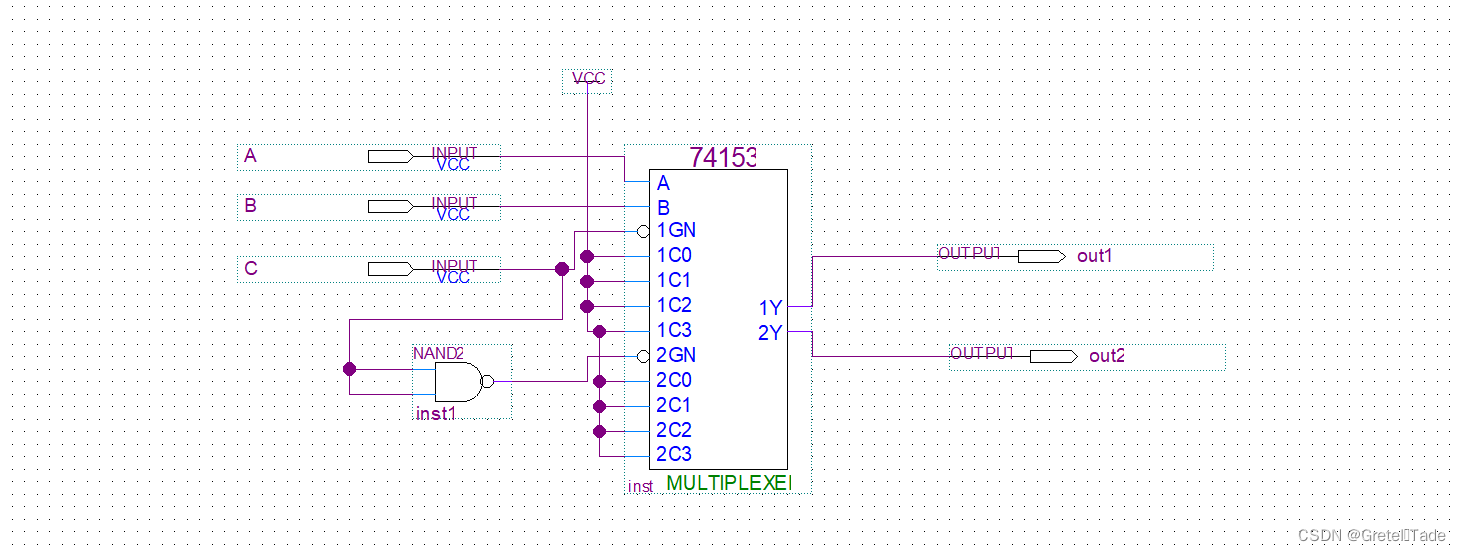
(注意,这里我的1C0~1C3和2C0到2C3输出口都是接高电平,这个可以根据实际情况去接高电平或者低电平。)
3.仿真结果
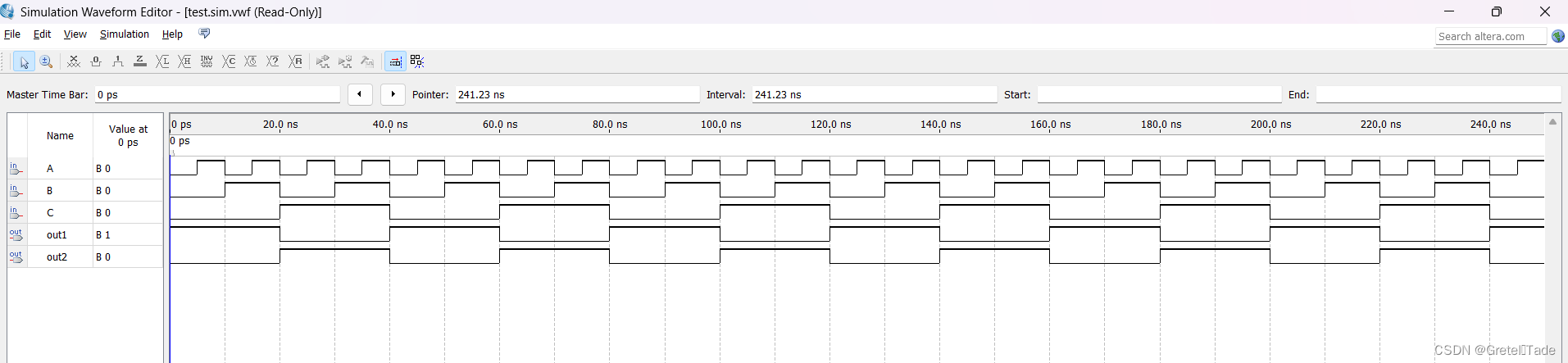
由于数据选择器是选择1C0~1C3和2C0到2C3这8个输出口输出的,我这里都是接高电平,那么输出结果要么是高位(OUT2)为1,要么是低位(OUT1)的为1。仿真结果无误。
三、8选1选择器的应用
1.三变量表决器
项目一 : 用指定芯片设计一个三变量表决器(即三个人对于某件事情进行表决,两个和两个以上同意则表决结果为通过,否则为不通过)。也就是说,输入端ABC,只要其中有两个或以上的输入1,那么结果就是通过,输出1。
真值表:
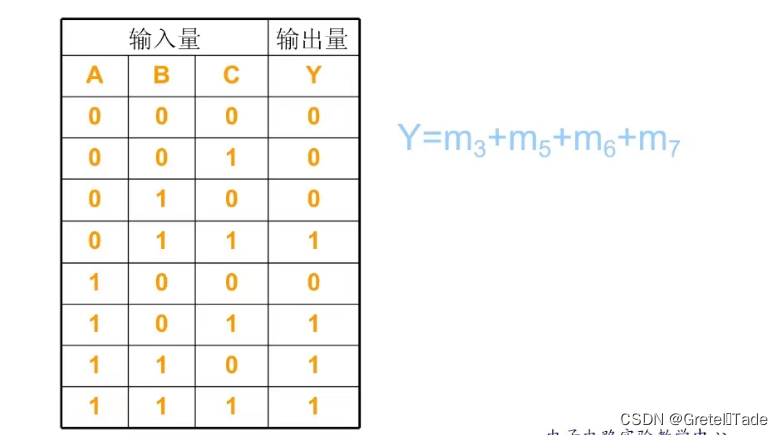
如下图,我们可以看到74ls153芯片,在不同的输入现在地址下的输出。要想实现三变量表决器的话,我们就需要根据上图的三变量表决器的真值表来去设置1C0~1C3和2C0到2C3这8个输出口输出的电平接口,很显然1C0,1C1,1C2,2C0这四个是接到低电平的,也就是直接接地,而剩下的四个就是接高电平的,直接接电源VCC。
电路连接图:
仿真结果如下所示: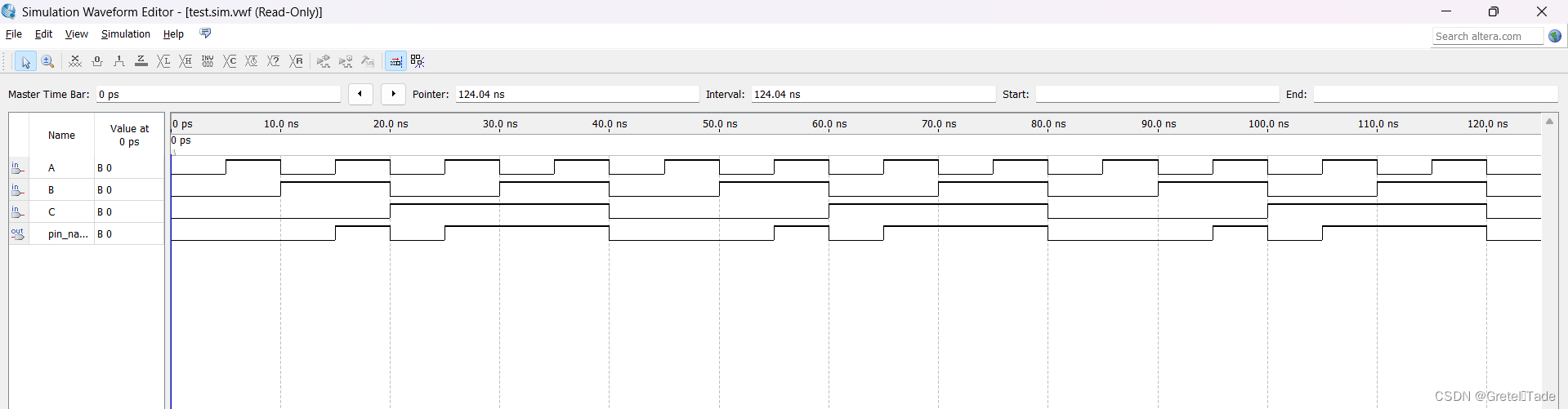
仿真无误,实验成功。
实际电路连接图:

2.奇偶校验电路
项目二 : 用指定芯片设计一个三位输入一位输出的奇偶校验电路(奇校验电路,当输入有奇数个 1 时, 输出为 1;偶校验电路当输入有偶数个 1 时,输出为 1。这里以奇校验电路为示例:
真值表:
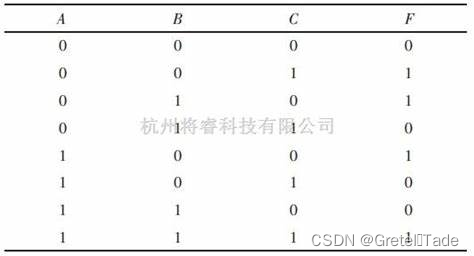
表达式:Y=m1+m2+m4+m7
同样的我们根据表达式,去对C0~1C3和2C0到2C3这8个输出口输出的电平接口设置,很显然,1C0,1C3,2C1,2C3这4个是接低电平的,直接接地,而另外四个就是接高电平。
电路连接图如下:
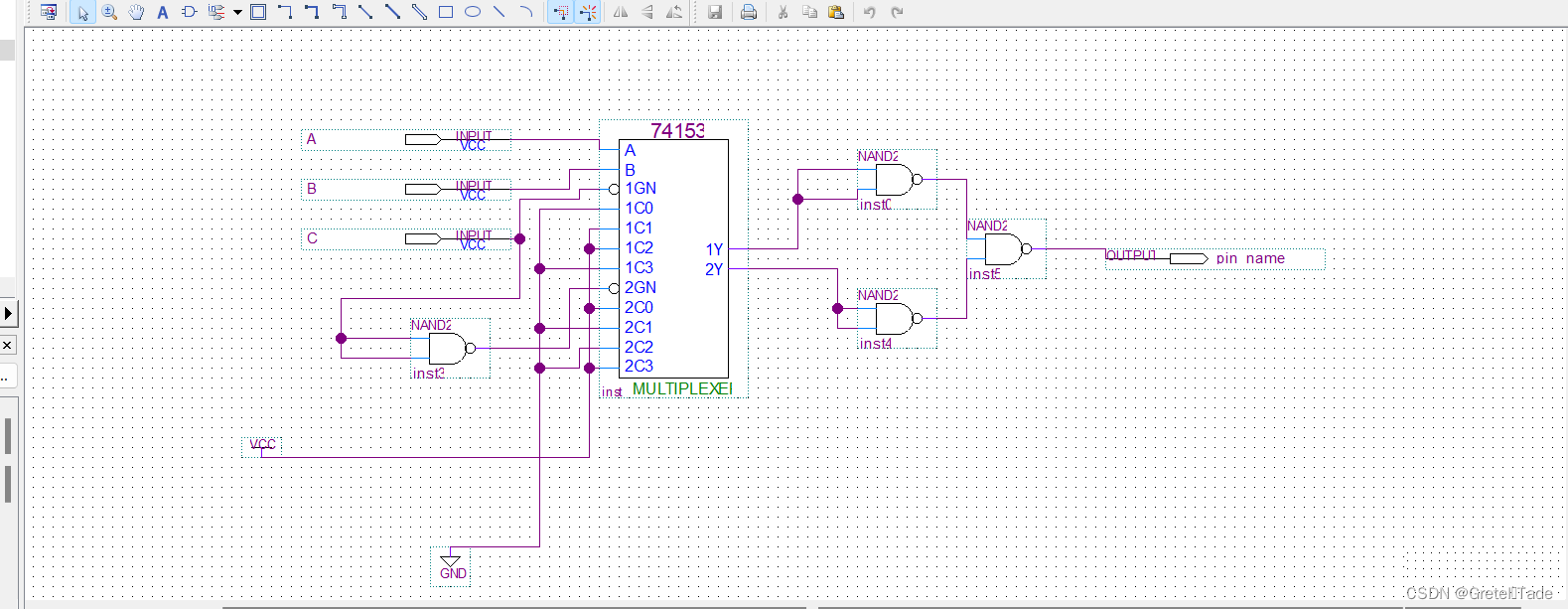
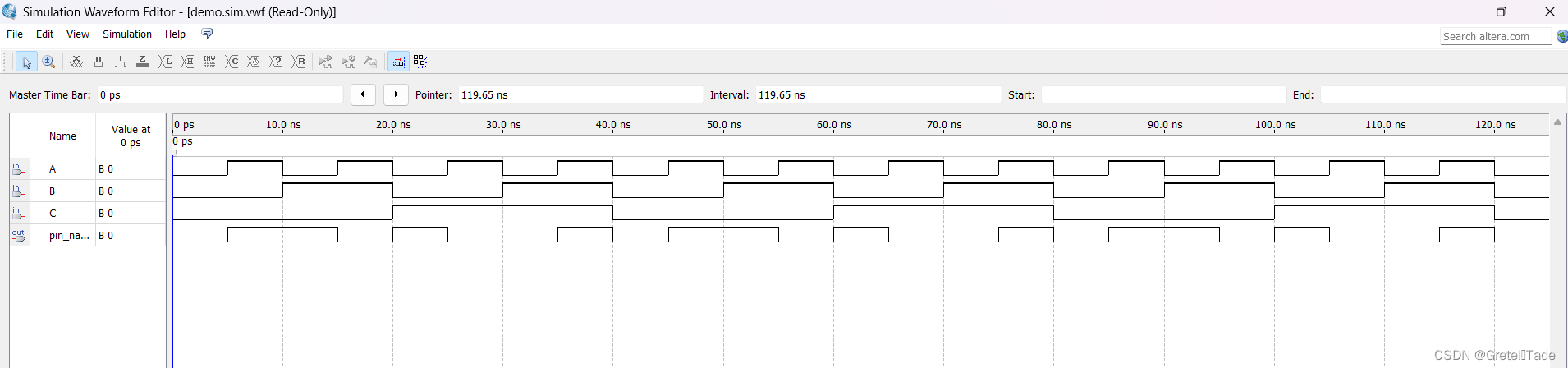
仿真结果:
这里我们可以看到,当A2,A1,A0其中一个输出一个高电平的时候,输出结果就是1,表示奇数,当三个都输入1的时候输出结果也是1,其他情况为0,那就说明仿真无误。
实验连接图忘记拍照了,不好意思哈!!!
以上就是本期的全部内容,喜欢的话给个赞吧!
分享一张壁纸:

相关文章:

数电实验-----实现74LS153芯片扩展为8选1时间选择器以及应用(Quartus II )
目录 一、74LS153芯片介绍 管脚图 功能表 二、4选1选择器扩展为8选1选择器 1.扩展原理 2.电路图连接(Quartus II ) 3.仿真结果 三、8选1选择器的应用 1.三变量表决器 2.奇偶校验电路 一、74LS153芯片介绍 74ls153芯片是属于四选一选择器的芯片。…...
如何实现MATLAB与Simulink的数据交互
参考链接:如何实现MATLAB与Simulink的数据交互 MATLAB是一款强大的数学计算软件,Simulink则是一种基于模型的多域仿真平台,常用于工程和科学领域中的系统设计、控制设计和信号处理等方面。MATLAB和Simulink都是MathWorks公司的产品࿰…...
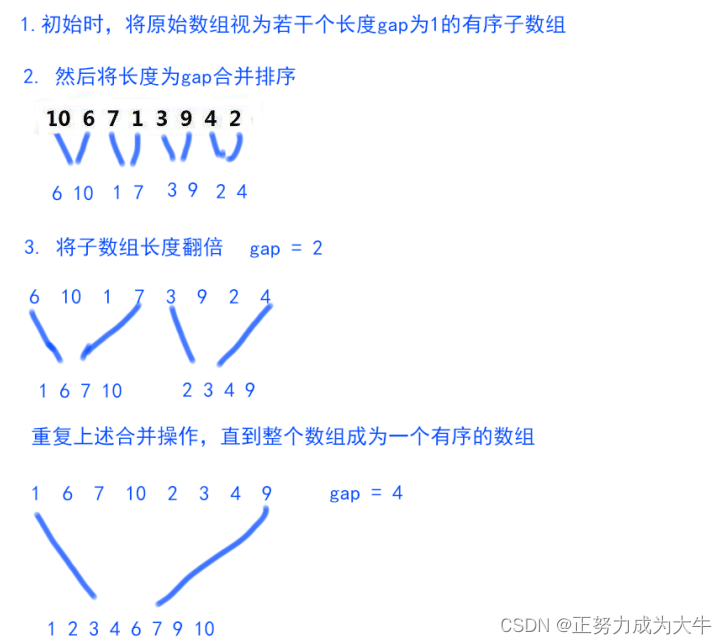
【数据结构】归并排序
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和算法 ✈️专栏:数据结构 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵 希望大佬指点一二 如果文章对你…...

数字引领,智慧赋能|袋鼠云与易知微共同亮相2023智慧港口大会
2023年10月19日,由中国港口协会、中国交通通信信息中心、天津港(集团)有限公司主办,中国港口协会智慧港口专业委员会、《港口科技》杂志社等单位承办的以“数字引领 智慧赋能”为主题的“2023智慧港口大会”在天津顺利召开。 袋鼠…...
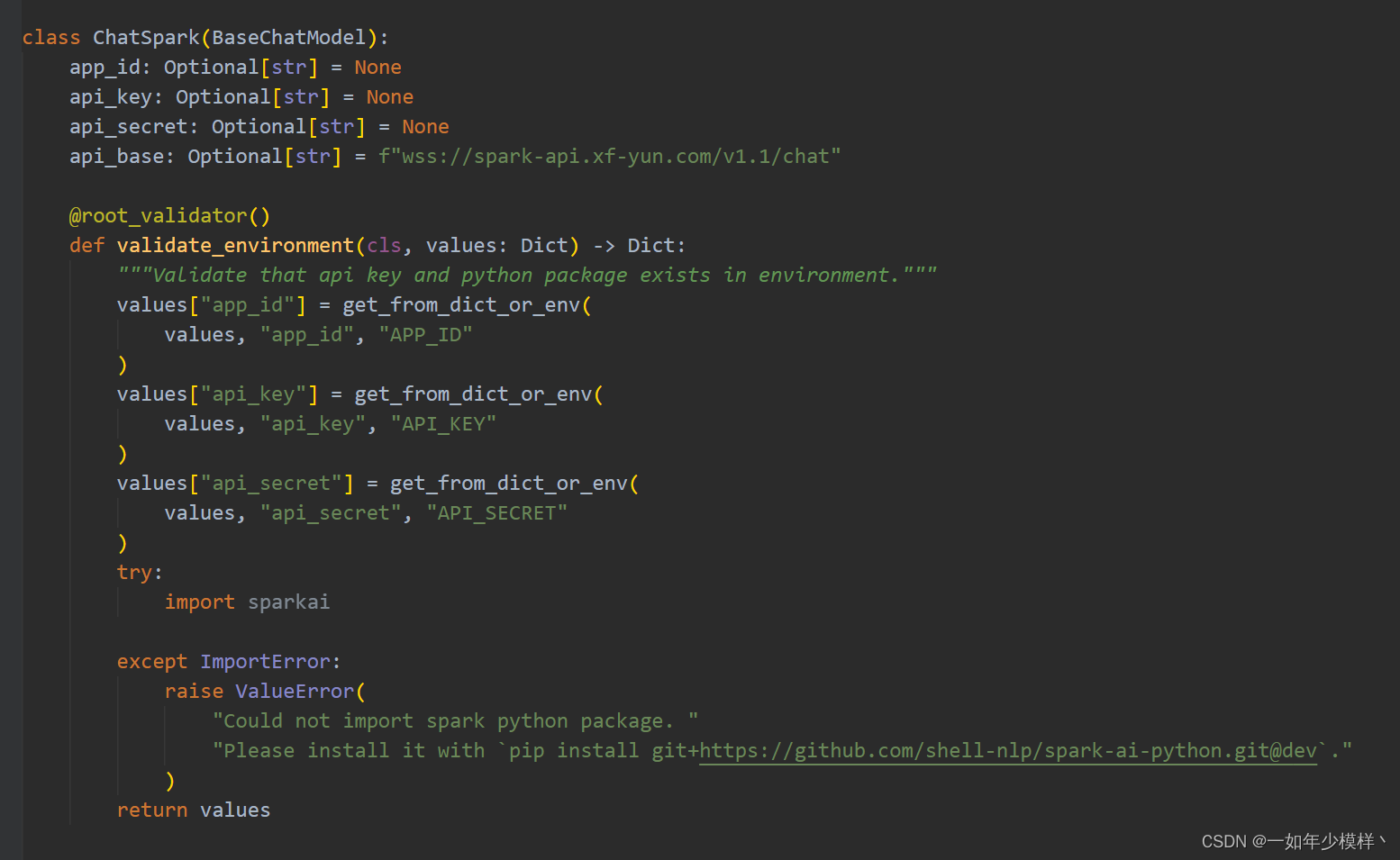
星火模型(Spark)的langchain 实现
星火模型的langchain实现 测试已通过,希望有所帮助。 使用前请先安装环境: pip install githttps://github.com/shell-nlp/spark-ai-python.git注意: 一定要使用上面方式安装spark库,因对官方的库做了改动。官方的库已经长时间不…...

python运算符重载之构造函数和迭代器
1 python运算符重载之构造函数和迭代器 python运算符重载是在类方法中拦截内置操作-当类的实例使用内置操作时,pytho自动调用对应方法,并且返回操作结果。 NO#描述1拦截运算运算符重载拦截内置操作,比如打印、函数调用、点号运算、表达式运…...

【数据处理】Python:实现求条件分布函数 | 求平均值方差和协方差 | 求函数函数期望值的函数 | 概率论
猛戳订阅! 👉 《一起玩蛇》🐍 💭 写在前面:本章我们将通过 Python 手动实现条件分布函数的计算,实现求平均值,方差和协方差函数,实现求函数期望值的函数。部署的测试代码放到文后了,运行所需环境 python version >= 3.6,numpy >= 1.15,nltk >= 3.4,tqd…...

new/delete 和malloc/free的区别
C中: 创建单个数据空间: char *ch new char; delete ch; ch NULL; 创建多个数据空间: char *ch new char[4]; delete [] ch; ch NULL; C语言中: 创建单个数据空间: char *ch malloc(sizeof(char)); fre…...

Linux程序设计(上)
系列文章目录 文章目录 系列文章目录前言一、unix, linux, GNU, POSIXLinux程序 二、shellshell语法1.变量2.语句 函数命令命令的执行dialog工具-- 三、文件操作1. Linux 文件结构2. 系统调用和设备驱动程序3. 库函数4. 底层文件访问5. 标准I/O库6.格式化输入输出7. 文件和目录…...

mysql面试题——存储引擎相关
一:MySQL 支持哪些存储引擎? MySQL支持多种存储引擎,比如InnoDB,MyISAM, MySQL大于等于5.5之后,默认存储引擎是InnoDB 二:InnoDB 和 MyISAM 有什么区别? InnoDB支持事务,MyISAM不支持InnoD…...

趣学python编程 (四、数据结构和算法介绍)
数据结构和算法在编程中非常重要。数据结构是组织和存储数据的方式,而算法是解决问题的方法和步骤。你要挑战的蓝桥杯,实际也是在设计算法解决问题。其实各种编程语言都只是工具,而程序的核心数据结构算法。犹如练武,数据结构和算…...
使用Pandas进行时间重采样,充分挖掘数据价值
大家好,时间序列数据蕴含着很大价值,通过重采样技术可以提升原始数据的表现形式。本文将介绍数据重采样方法和工具,提升数据可视化技巧。 在进行时间数据可视化时,数据重采样是至关重要且非常有用的,它支持控制数据的…...
Django(九、choices参数的使用、多对多表的三种创建方式、Ajax技术)
文章目录 一、choices参数choices参数的用法choices 参数用法总结 二、MVC与MTV模式1.MVC2.MTV 三、多对多的三种创建方式1.全自动创建2.纯手动创建半自动创建 四、Django与Ajax1.什么是Ajax常见的场景Ajax案例 一、choices参数 在没有用到choices参数之前,我们在D…...

德语B级SampleAcademy
德语B级 一, 反身代词(1)A 主语和宾语一致(2)D 双宾语,主语与直接宾语不一致(3), 补充单词(4)真反身代词(5)假反身代词(6)真假反身代词(7)相互反身(8)非反身#反身#相互反身 二,Nomen…...

vue3自定义hooks
获取dom的id属性 index.ts import { onMounted } from "vue" type option {el: string }export default function(option:option):Promise<{name: string}> {return new Promise((resolve)>{onMounted(()>{const dom:HTMLElement document.querySele…...

Consistency Models 阅读笔记
简介 Diffusion models需要多步迭代采样才能生成一张图片,这导致生成速度很慢。一致性模型(Consistency models)的提出是为了加速生成过程。 Consistency models可以直接一步采样就生成图片,但是也允许进行多步采样来提高生成的质…...

杭电oj 2034 人见人爱A-B C语言
此处的c和a指向同一块内存空间,改变c就是改变a,反之亦然,此处是为了方便看这么写的,如果不想c和a指向同一空间请分别开辟空间(即不如此写camalloc) #include<stdio.h> #include<stdlib.h>int …...
)
springboot(ssm大学生成绩管理系统 成绩管理平台Java(codeLW)
springboot(ssm大学生成绩管理系统 成绩管理平台Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0&…...

SOME/IP 协议介绍(五)指南
指南(信息性) 选择传输协议 SOME/IP直接支持互联网上使用最广泛的两种传输协议:用户数据报协议(UDP)和传输控制协议(TCP)。UDP是一种非常简洁的传输协议,仅支持最重要的功能&#…...
Python调用企微机器人: 发送常用格式汇总
企微接口文档 发送应用消息 - 接口文档 - 企业微信开发者中心 发送格式 应用支持推送文本、图片、视频、文件、图文等类型。 ~~~以下列举常用格式 示例~~~ 1.发送文本 代码如下: def sendtxt_robotmsg(self):# 正式keywx_key "xx"wx_webhookurl htt…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
