二维偏序问题
偏序
偏序(Partial Order)的概念:
设 A 是一个非空集,P 是 A 上的一个关系,若 P 满足下列条件:
- Ⅰ 对任意的 a ∈ A,(a, a) ∈ P;(自反性 reflexlve)
- Ⅱ 若 (a, b) ∈ P,且 (b, a) ∈ P,则 a = b;(反对称性,anti-symmentric)
- Ⅲ 若 (a, b) ∈ P,(b, c) ∈ P,则 (a, c) ∈ P;(传递性,transitive)
则称 P 是 A 上的一个偏序关系,通常记作 ≼。注意这里的 ≼ 不必是指一般意义上的"小于或等于"。
若 P 是 A 上的一个偏序关系,用 a ≼ b 来表示 (a, b) ∈ P。
整除关系便是一个定义在自然数上的一个偏序关系 |,3 | 6 的含义是 3 整除 6。大于或等于也是定义在自然数集上的一个偏序关系。
偏序关系
一个关系具有自反,反对称,传递的特性,就叫做偏序关系。一个集合 S 和一个偏序关系 < 并称为偏序集,写作(S,<)。例如大于等于符号就是一个偏序关系。
可比性
两个元素具有偏序关系,要么 a < b,要么 b < a,则称为 a 和 b 可比。否则称为不可比。例如(Z+,|)中,2不能整除5,2和5就是不可比的。
全序关系
相关文章:

二维偏序问题
偏序 偏序(Partial Order)的概念: 设 A 是一个非空集,P 是 A 上的一个关系,若 P 满足下列条件: Ⅰ 对任意的 a ∈ A,(a, a) ∈ P;(自反性 reflexlve)Ⅱ 若 (a, b) ∈ P,且 (b, a) ∈ P,则 a = b;(反对称性,anti-symmentric)Ⅲ 若 (a, b) ∈ P,(b, c) ∈ P,则 (a,…...

解析Spring Boot中的CommandLineRunner和ApplicationRunner:用法、区别和适用场景详解
在Spring Boot应用程序中,CommandLineRunner和ApplicationRunner是两个重要的接口,它们允许我们在应用程序启动后执行一些初始化任务。本文将介绍CommandLineRunner和ApplicationRunner的区别,并提供代码示例和使用场景,让我们更好…...

谷歌浏览器版本下载
Chrome 已是最新版本 版本 119.0.6045.160(正式版本) (64 位) 自定义chrome https://www.sysgeek.cn/chrome-new-tab-page-customize/ chrome怎么把标签放主页 https://g.pconline.com.cn/x/1615/16153935.html 谷歌浏览器怎么设…...

js 打开页面的方法总结
文章目录 前言1.window.open2.location.href / window.location.href3.location.replace4.a标签跳转 前言 本文总结 JS 打开新页面/窗口的方法 1.window.open 打开一个新的浏览器页面或者标签页,可以设置新页面的参数 window.open(url,name,specs,replace)参数1:url a. 必须…...
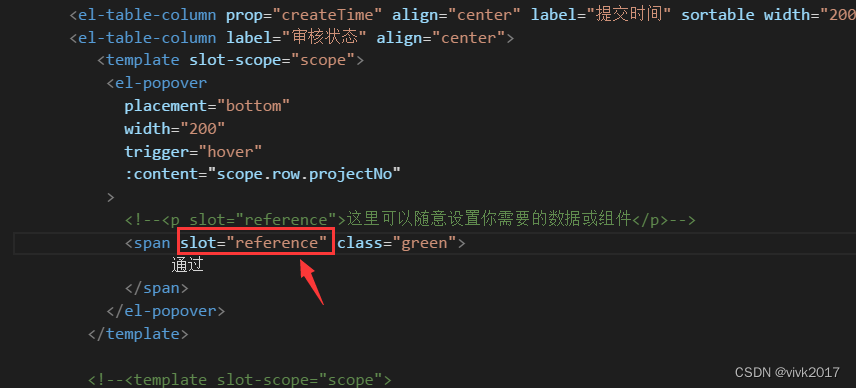
element UI表格中设置文字提示(tooltip)或弹出框(popover)时候注意的地方
在表格中自定义内容的时候需要使用标签,否则无法正常显示 文档中有两种写法:1、使用 slot“reference” 的具名插槽,2、使用自定义指令v-popover指向 Popover 的索引ref。 使用tooltip 时用具名 slot 分发content,替代tooltip中…...
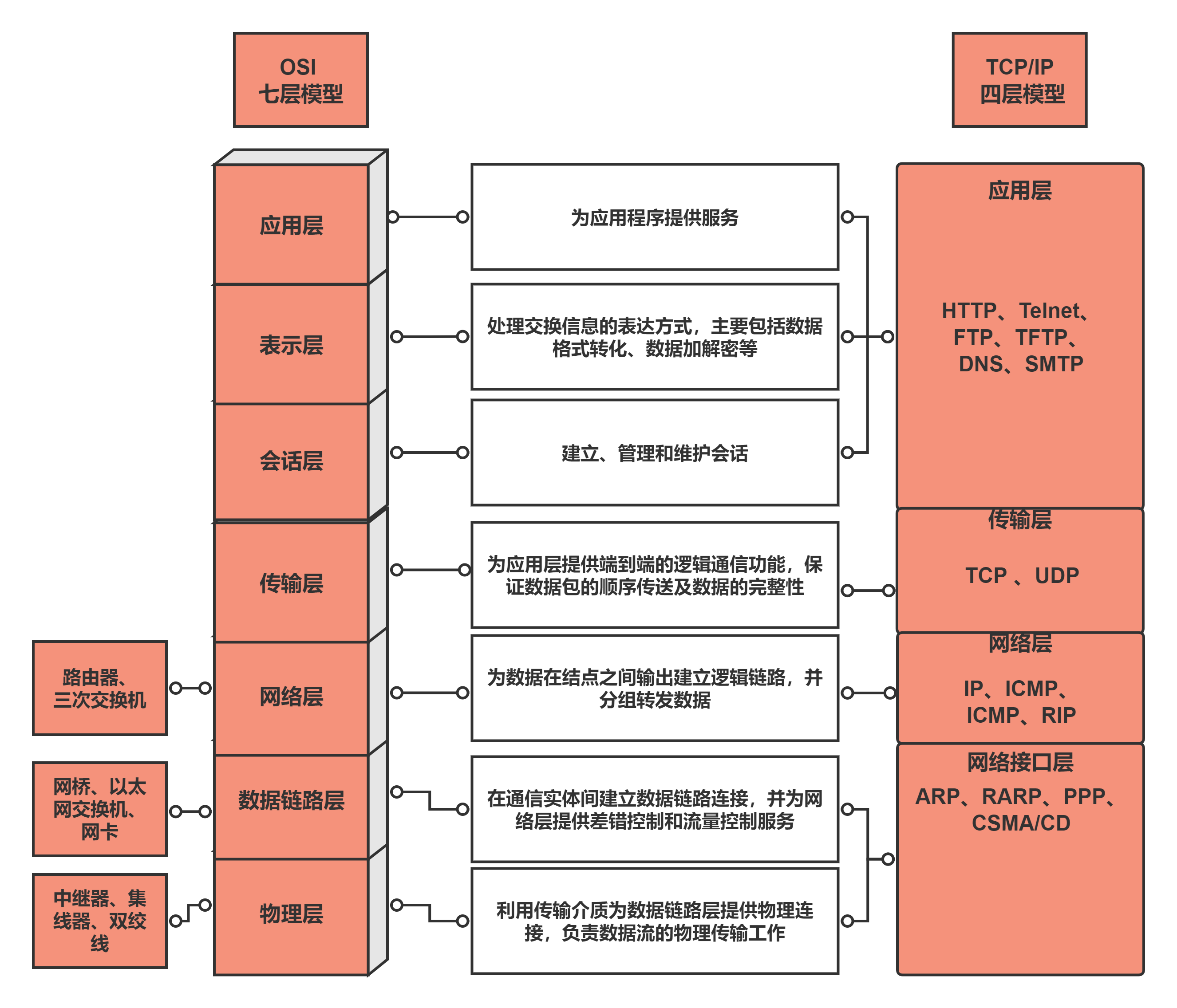
【网络】OSI模型 与 TCP/IP模型 对比
一、OSI模型 OSI模型包含7个层次,从下到上分别是: 1. 物理层(Physical Layer) - 功能:处理与电子设备物理接口相关的细节(如电压、引脚布局、同步,等等)。 - 协议:以…...

[Docker]记一次使用jenkins将镜像文件推送到Harbor遇到的问题
系统版本: Ubuntu 18.01 私服: Harbor Docker版本: Docker version 18.09.5 首先需要明确的是,即在harbor里项目设置为公开,但是在push的时候还是需要用户验证的,即需要使用docker登录 docker login harbo…...

龙芯 Loongson 架构 UOS 系统编译 Qt 5.15.2 源码
背景 需要在龙芯(Loongson)CPU,UOS 系统下,进行国产化项目适配,UOS 自带 Qt 5.11,但是版本过老,与目前基于 Qt 5.15.2 项目存在不兼容情况,故需要自行编译 Qt 5.15.2开发环境。 软…...

【IDEA 使用easyAPI、easyYapi、Apifox helper等插件时,导出接口文档缺少代码字段注释的相关内容、校验规则的解决方法】
问题 IDEA 使用easyAPI、easyYapi、Apifox helper等插件时,导出的接口文档上面,缺少我们代码里的注解字段,如我们规定了NOTNULL、字段描述等。 问题链接,几个月之前碰到过,并提问了,到现在解决,…...
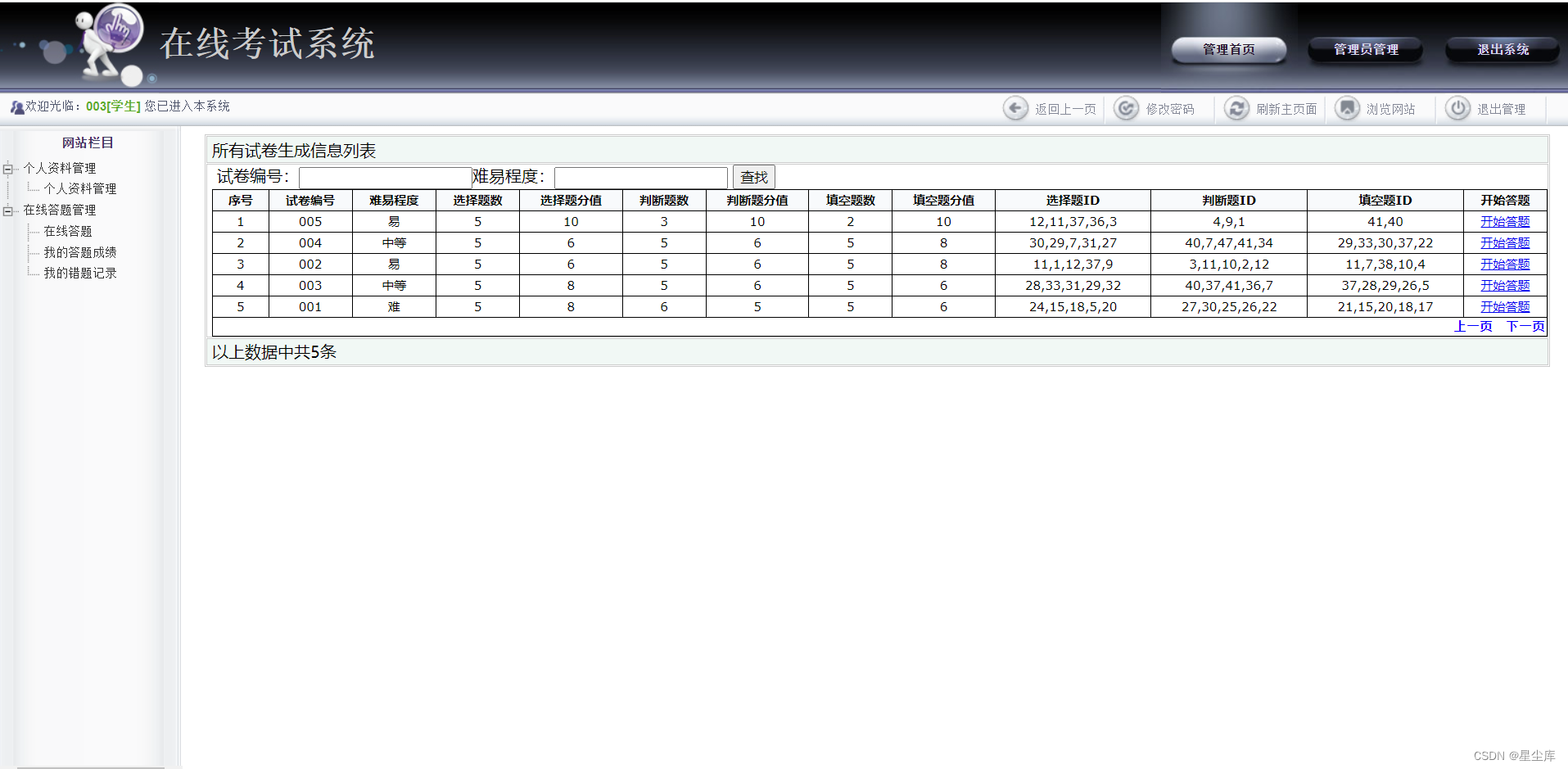
asp.net在线考试系统+sqlserver数据库
asp.net在线考试系统sqlserver数据库主要技术: 基于asp.net架构和sql server数据库 功能模块: 首页 登陆 用户角色 管理员(对老师和学生用户的增删改查),老师(题库管理 选择题添加 选择题查询 判断题添加…...

CRM按行业细分的重要性
很多企业和销售会诟病CRM系统不够贴合行业、功能也不够细分和实用。因为各行各业的业务千差万别,所以功能完备、使用满意度高的CRM一定是与不同行业业务场景高度匹配的,是深度行业化的。因此行业化是CRM发展的重要趋势之一,为什么CRM一定要走…...

自动化测试测试框架封装改造
PO模式自动化测试用例 PO设计模式是自动化测试中最佳的设计模式,主要体现在对界面交互细节的封装,在实际测试中只关注业务流程就可以了。 相较于传统的设计,在新增测试用例后PO模式有如下优点: 1、易读性强 2、可扩展性好 3、…...

C#可空类型
在C#中,可空类型(Nullable types)允许值类型(比如int, double, bool等)接受null值。这是特别有用的,因为在很多应用程序中,如数据库交互和数据解析,值类型的字段可能需要表示没有值&…...

R语言:利用biomod2进行生态位建模
在这里主要是分享一个不错的代码,喜欢的可以慢慢研究。我看了一遍,觉得里面有很多有意思的东西,供大家学习和参考。 利用PCA轴总结的70个环境变量,利用biomod2进行生态位建模: #------------------------------------…...

如何学习算法
在不知其所以然的情况下,算法只是一堆离散的机械步骤,缺少背后的思想的支撑, 这些步骤之间就没有一个本质层面上的关联(先知亚里士多德早就指出:学习即联接)。 所以就跟背历史书也没多大区别。然而…...

MFC/QT 一些快要遗忘的细节:
1:企业应用中,MFC平台除了用常见的对话框模式还有一种常用的就是单文档模式, 维护别人的代码,不容易区分,其实找与程序同名的cpp就知道了,比如项目名称为 DoCMFCDemo,那么就看BOOL CDocMFCDemoApp::InitI…...

常见的面试算法题:阶乘、回文、斐波那契数列
1.阶乘算法 Factorial 例如:给出数字5,对其以下的的每个数字相乘,结果等于120 解:递归 Recursive function factorial(n) {// 如果n为0或1,阶乘是1if (n 0 || n 1) {return 1;}// 否则,返回n乘以n-1的…...

微服务 Spring Cloud 7,Nacos配置中心的Pull原理,附源码
目录 一、本地配置二、配置中心1、以Nacos为例:2、Pull模式3、也可以通过Nacos实现注册中心 三、配置中心提供了哪些功能四、如何操作配置中心1、配置注册2、配置反注册3、配置查看4、配置变更订阅 五、主流的微服务注册中心有哪些,如何选择?…...

c#Nettonsoft.net库常用的方法json序列化反序列化
Newtonsoft.Json 是一个流行的 JSON 操作库,用于在 .NET 应用程序中序列化、反序列化和操作 JSON 数据。下面是 Newtonsoft.Json 常用的一些方法: 序列化对象为 JSON 字符串: string json JsonConvert.SerializeObject(obj);var obj new {…...

力扣刷题-二叉树-二叉树的高度与深度
二叉树最大深度 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 递归法 本题可以使用前序(中左…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
