【每日刷题——语音信号篇】
思考与练习
练习2.1
- 语音信号在产生的过程中,以及被感知的过程中,分别要经过人体的哪些器官?
1.产生过程:
肺部空气 → \rightarrow →冲击声带 → \rightarrow →通过声道(可以调节) → \rightarrow →发出不同声音
2.感知过程:
空气传播 → \rightarrow →进入人耳 → \rightarrow →鼓膜震动 → \rightarrow →听小骨 → \rightarrow →耳蜗 → \rightarrow →电信号 → \rightarrow →中枢听觉系统
练习2.2
- 汉语拼音的声调,对应的是语音信号的哪种特征?
1.基频:一段信号有10Hz和100Hz叠加而成,那么基频就是10Hz,如图1所示。
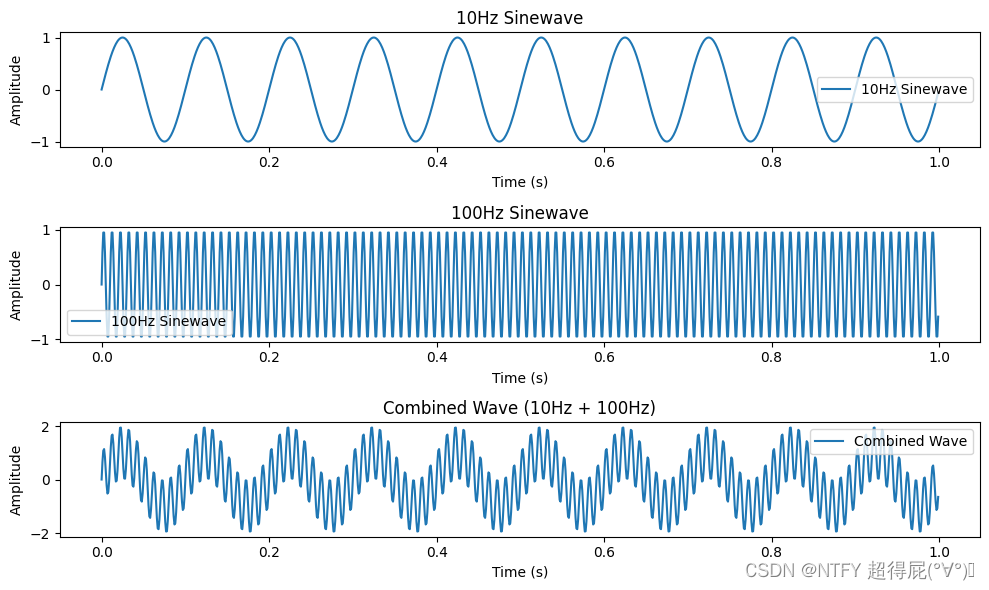
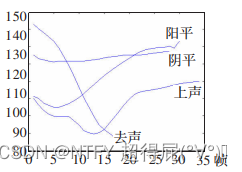
2.基音轨迹: 信号以横轴为时间,纵轴为基频得到的曲线。汉语拼音四声如图2所示 1 ^1 1。
练习2.3
- 人耳听觉的非线性是由哪些因素造成的?
人耳构造非线性:
1.外耳:耳翼、外耳道、鼓膜,外耳道看似一条管道,有许多共振频率,对某些频率的声音进行放大。
2.中耳:通过三块听小骨传到内耳,在一定声强范围内,传递是线性的,超出一定范围,这种传递变成非线性的(保护内耳)
3.内耳:耳蜗依靠毛细胞将机械振动(耳蜗中流体速度变化)转化电信号,耳蜗不同位置的毛细胞,对应不同频率声音,分布大致按频率对数分布。
非线性体现在两方面:对频率感知的非线性,对声强感知的非线性。

练习2.4
- 动圈式麦克风的工作原理是什么?与电容式麦克风相比,动圈式麦克风有哪些优缺点?
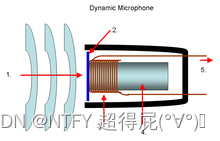
1.工作原理:当声波使膜片振动时,连接在膜片上的线圈随着一起振动,产生感应电流(电信号),通过信号放大器,并从扬声器发出声音。
2.优缺点:优点有不需要直流工作电压,缺点包括灵敏度低。
练习2.5
- 编写一段程序,利用μ-law 变换的公式,将16 位线性脉冲编码格式存储的音频转换为8 位非线性脉冲编码格式,并比较转换前后音频的声音质量及文件大小。
sox input.wav -e mu-law -b 8 output.wav
sox input.wav -e mu-law output1.wav
output.wav和output1.wav一样大小,均为input.wav一半。上面两行代码一直,表示 μ − law \mu-\text{law} μ−law默认为8位
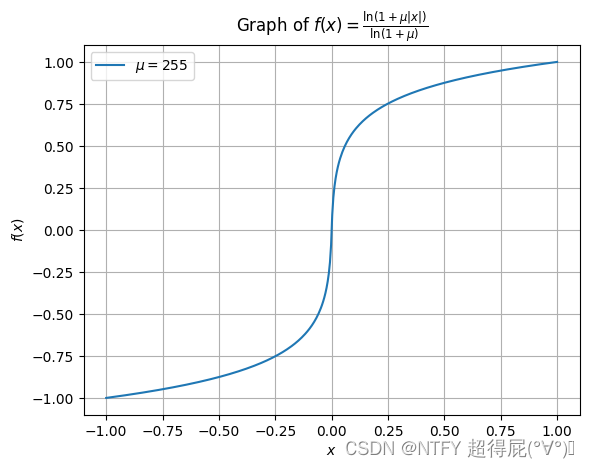
μ − law \mu-\text{law} μ−law公式为:
f ( x ) = sgn ( x ) ln ( 1 + μ ∣ x ∣ ) ln ( 1 + μ ) f(x) =\text{sgn}(x)\frac{\text{ln}(1+\mu|x|)}{\text{ln}(1+\mu)} f(x)=sgn(x)ln(1+μ)ln(1+μ∣x∣)
练习2.6
- 窗函数的作用是什么?有哪些常见的窗函数?
作用:
1.吉布斯现象(Gibbs phenomenon):在不连续点出产生高频分量,导致傅里叶变换后的频谱出现局部峰值。
2.频谱泄露:周期信号在分帧过程中被截断,导致频谱在整个频带内发生拖尾现象。
常见的窗函数:
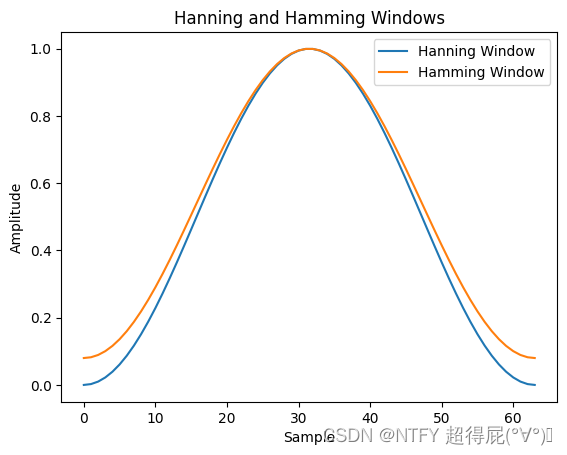
1.汉宁窗:
α = 0.5 \alpha=0.5 α=0.5
2.汉明窗:
α = 0.46 \alpha=0.46 α=0.46
ω [ n ] = ( 1 − α ) − α c o s 2 π n N − 1 \omega[n]=(1-\alpha)-\alpha cos\frac{2\pi n}{N-1} ω[n]=(1−α)−αcosN−12πn
练习2.7
- 编写一段程序,用以计算一段有限离散信号的离散傅里叶变换。
import scipy
import matplotlib.pyplot as plt
import numpy as np# 读取音频文件
rate, data = scipy.io.wavfile.read("resampled.wav")# 计算 STFT
f, t, Z = scipy.signal.stft(data, fs=rate, window='hann', nperseg=400, noverlap=240,nfft=None, detrend=False, return_onesided=True,boundary='zeros', padded=True, axis=-1
)# 绘制音频波形
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(data)
plt.title('Audio Waveform')
plt.xlabel('Sample')
plt.ylabel('Amplitude')# 绘制频谱
plt.subplot(2, 1, 2)
plt.pcolormesh(t, f, 10 * np.log10(np.abs(Z)), shading='auto')
plt.title('Spectrogram')
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.colorbar()
plt.tight_layout()
plt.show()
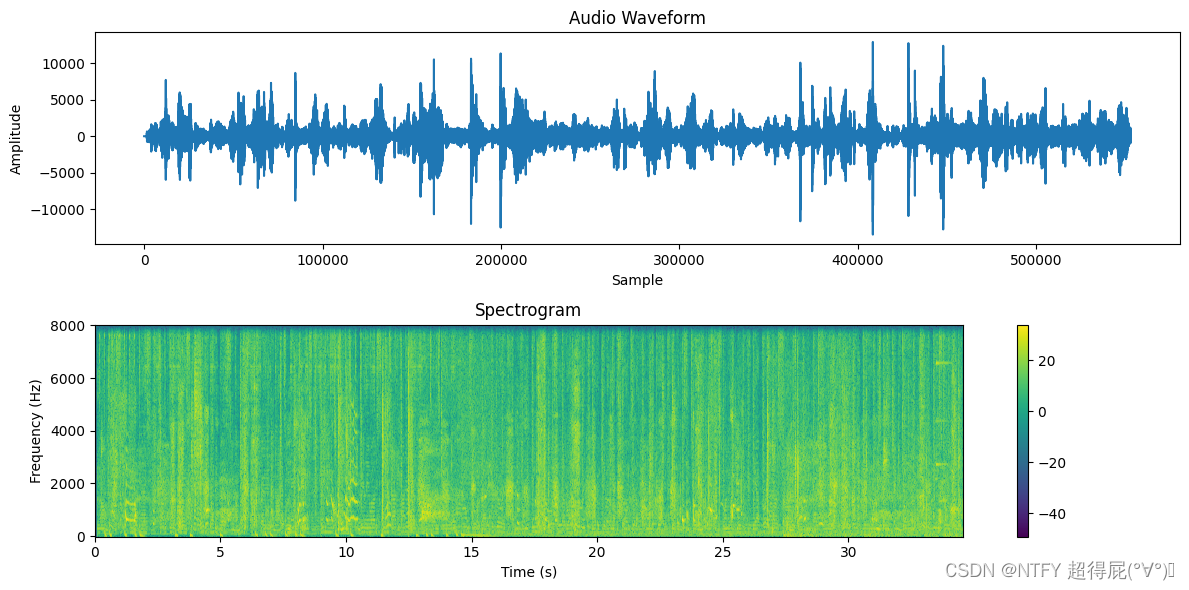
练习2.8
- 感知线性预测与梅尔倒谱系数在设计与实现上有哪些相同点与不同点?
1.相同点:频域转换使用SIFT,最终系数都采用IDFT
2.不同点: - 1 ^{1} 1PLP通过对功率谱进行巴克刻度变换,再与临界频带滤波器组卷积,结果通过等响度曲线预加重,而MFCC在第一步先进行预加重。
- 2 ^{2} 2频率校正:PLP系数通过巴克刻度、临界频带
- 3 ^{3} 3声强校正:PLP采用 y = x 1 3 y=x^\frac{1}{3} y=x31,MFCC采用 y = log x y=\text{log}x y=logx
练习2.9
- 除了LibROSA,还有一些基于Python 语言的音频特征提取工具库。下载并熟悉pyAudioAnalysis 与python_speech_features 工具库,利用其从音频中提取特征并进行可视化。
- pyAudioAnalysis教程
- python_speech_features教程
参考文献
- 宋刚, 姚艳红. 用于汉语拼音单音节声调识别的基频轨迹拟合方法[J]. 计算机工程与应用, 2008, 44(29):239-240.
相关文章:

【每日刷题——语音信号篇】
思考与练习 练习2.1 语音信号在产生的过程中,以及被感知的过程中,分别要经过人体的哪些器官? 1.产生过程: 肺部空气 → \rightarrow →冲击声带 → \rightarrow →通过声道(可以调节) → \rightarrow →…...

Linux进程通信——IPC、管道、FIFO的引入
进程间的通信——IPC 进程间通信 (IPC,InterProcess Communication) 是指在不同进程之间传播或交换信息。 IPC的方式通常有管道 (包括无名管道和命名管道) 、消息队列、信号量、共享存储、Socket、Streams等。其中 Socket和Streams支持不同主机上的两个进程IPC。 …...
)
数理统计的基本概念(一)
文章目录 总体、样本与统计量总体及其分布样本及其分布统计量统计量概念样本矩顺序统计量及其分布样本中位数与样本极差经验分布函数 参考文献 总体、样本与统计量 总体及其分布 在数理统计中,称所研究的对象的全体为总体,总体中的元素称为个体。若总体…...
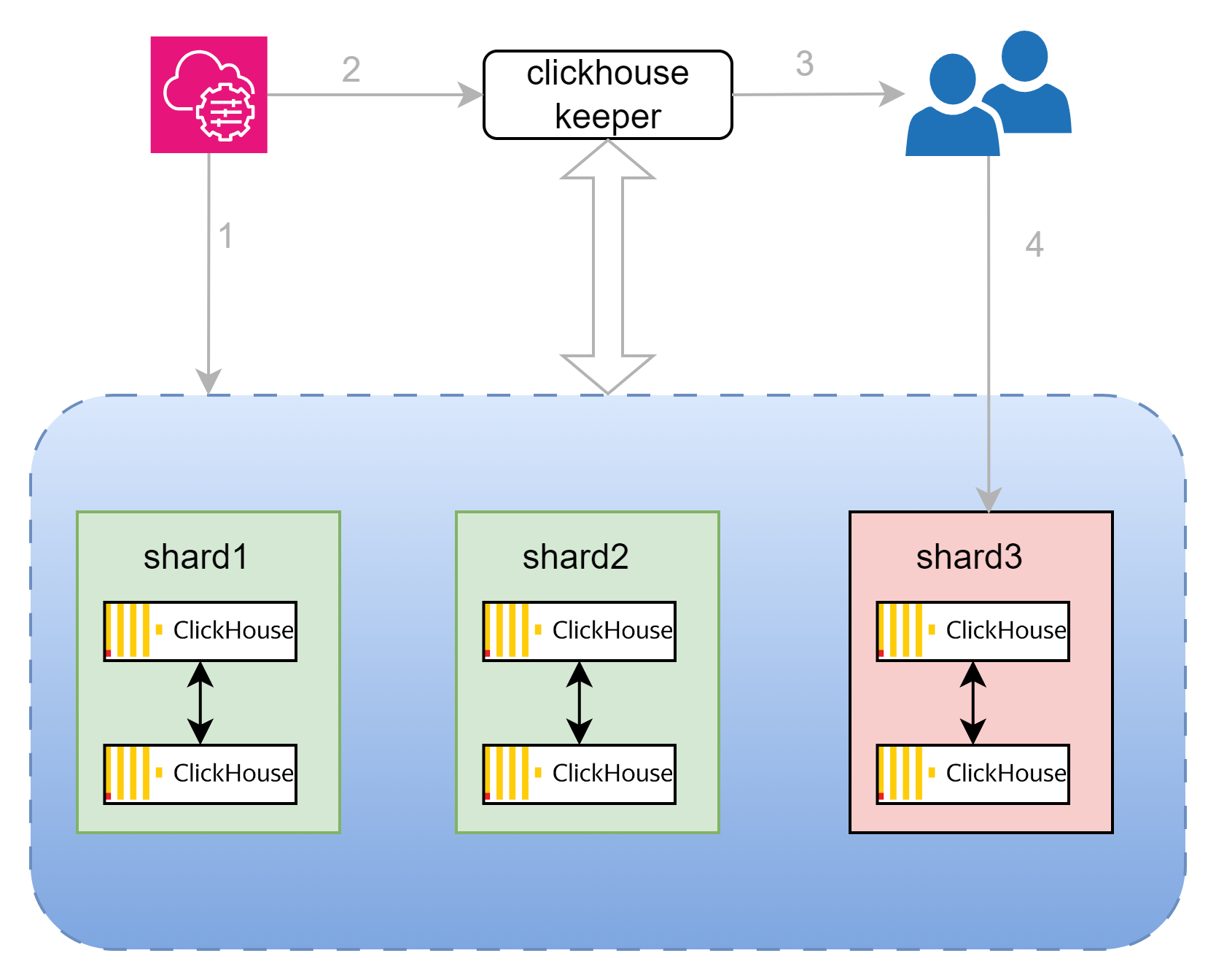
clickhouse分布式之弹性扩缩容的故事
现状 社区不支持喔,以后也不会有了。曾经尝试过,难道是是太难了,无法实现吗?因为他们企业版支持了,可能是利益相关吧,谁知道呢,毕竟开源也要赚钱,谁乐意一直付出没有回报呢。 社区…...
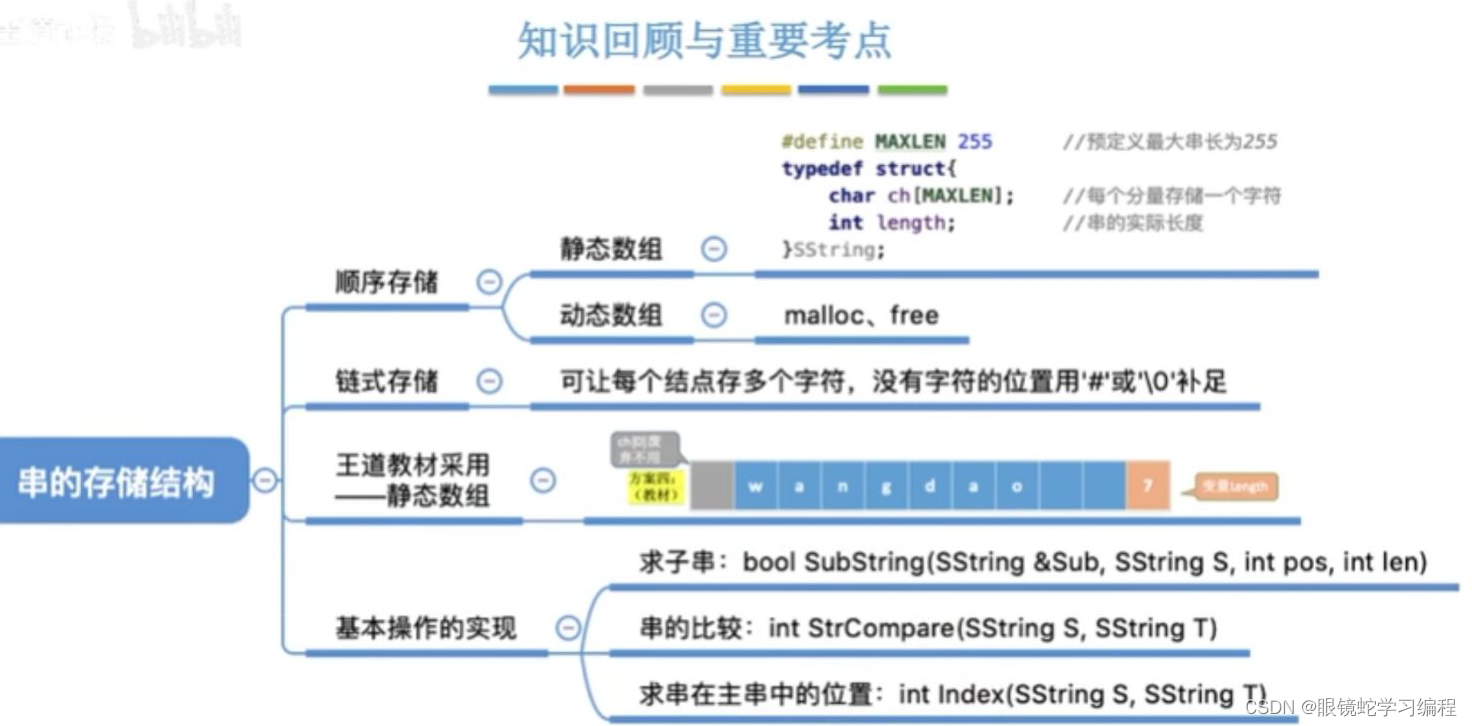
数据结构--串的基本概念
目录 串的基本概念 串的定义 串与线性表对比 串的基本操作 串的比较 字符集编码 乱码问题编辑 总结 串的存储结构 串的顺序存储编辑 串的链式存储 串的基本操作 1、求字串 2、比较 3、定位操作 总结 串的基本概念 串的定义 串与线性表对比 串的…...

音视频流媒体之 IJKPlayer FFmpeg Android 编译
FIJK dockerfile 编译环境 FROM --platformlinux/amd64 ubuntu:18.04RUN apt-get update && apt-get install -y \wget \unzip \git \gcc \g \make \python \yasm \pkg-config \protobuf-compiler \sudoRUN apt-get install -y openjdk-8-jdkENV ANDROID_HOME…...
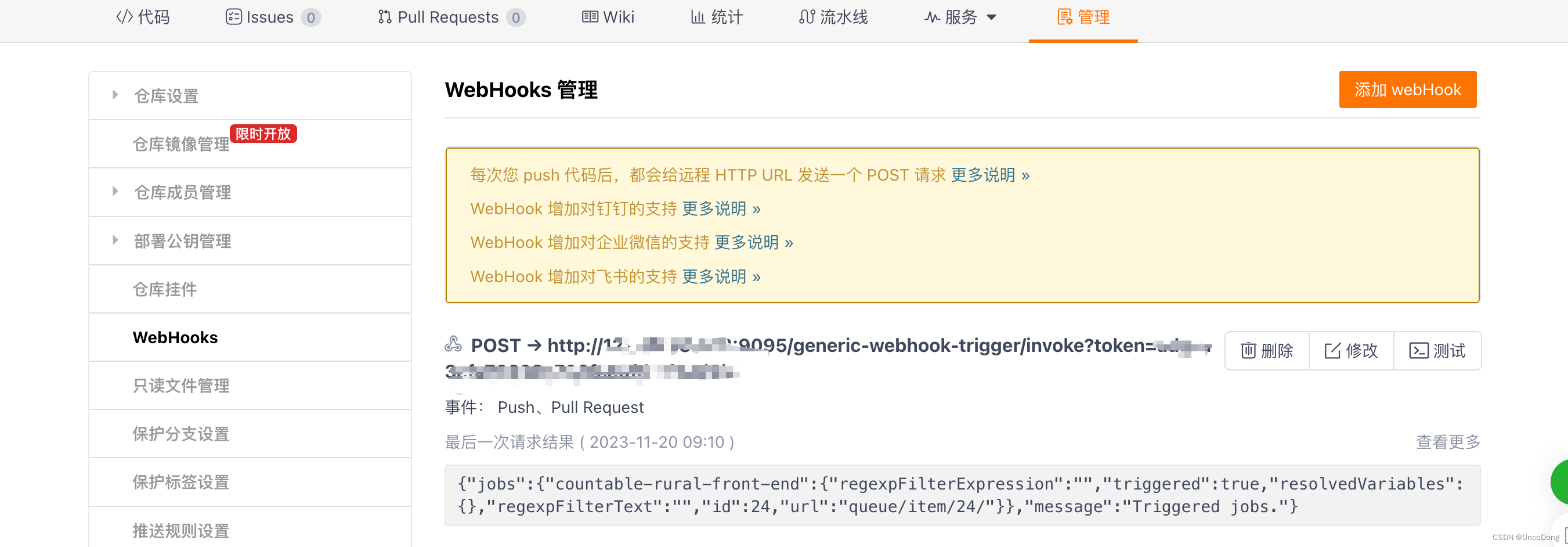
记录一次较为完整的Jenkins发布流程
文章目录 1. Jenkins安装1.1 Jenkins Docker安装1.2 Jenkins apt-get install安装 2. 关联github/gitee服务与webhook2.1 配置ssh2.2 Jenkins关联2.3 WebHook 3. 前后端关联发布 1. Jenkins安装 1.1 Jenkins Docker安装 Docker很好,但是我没有玩明白如何使用Docke…...
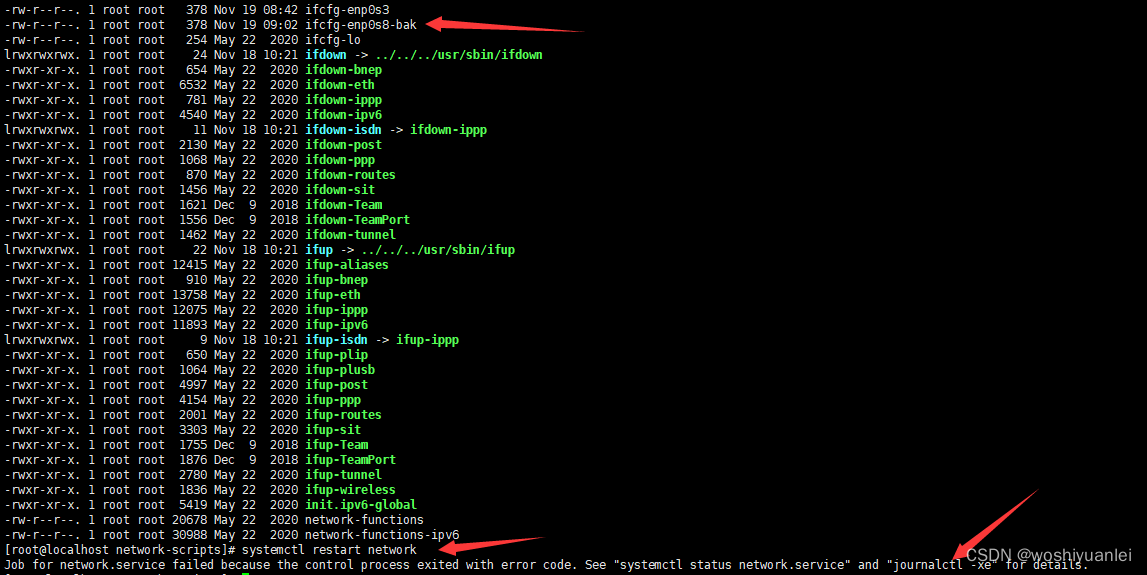
Virtual安装centos后,xshell连接centos 测试及遇到的坑
首先来一张官方的图--各种网络模式对应的连接状况: 1. 网络使用Host-Only模式动态分配IP,点确定后,centos 上运行 system restart network ,使用ifconfig查看新的ip,XShell可以直接连上centos, 但是由于使用…...
)
【算法】最优乘车——bfs(stringsteam的实际应用,getline实际应用)
题目 H 城是一个旅游胜地,每年都有成千上万的人前来观光。 为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路。 每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,…...
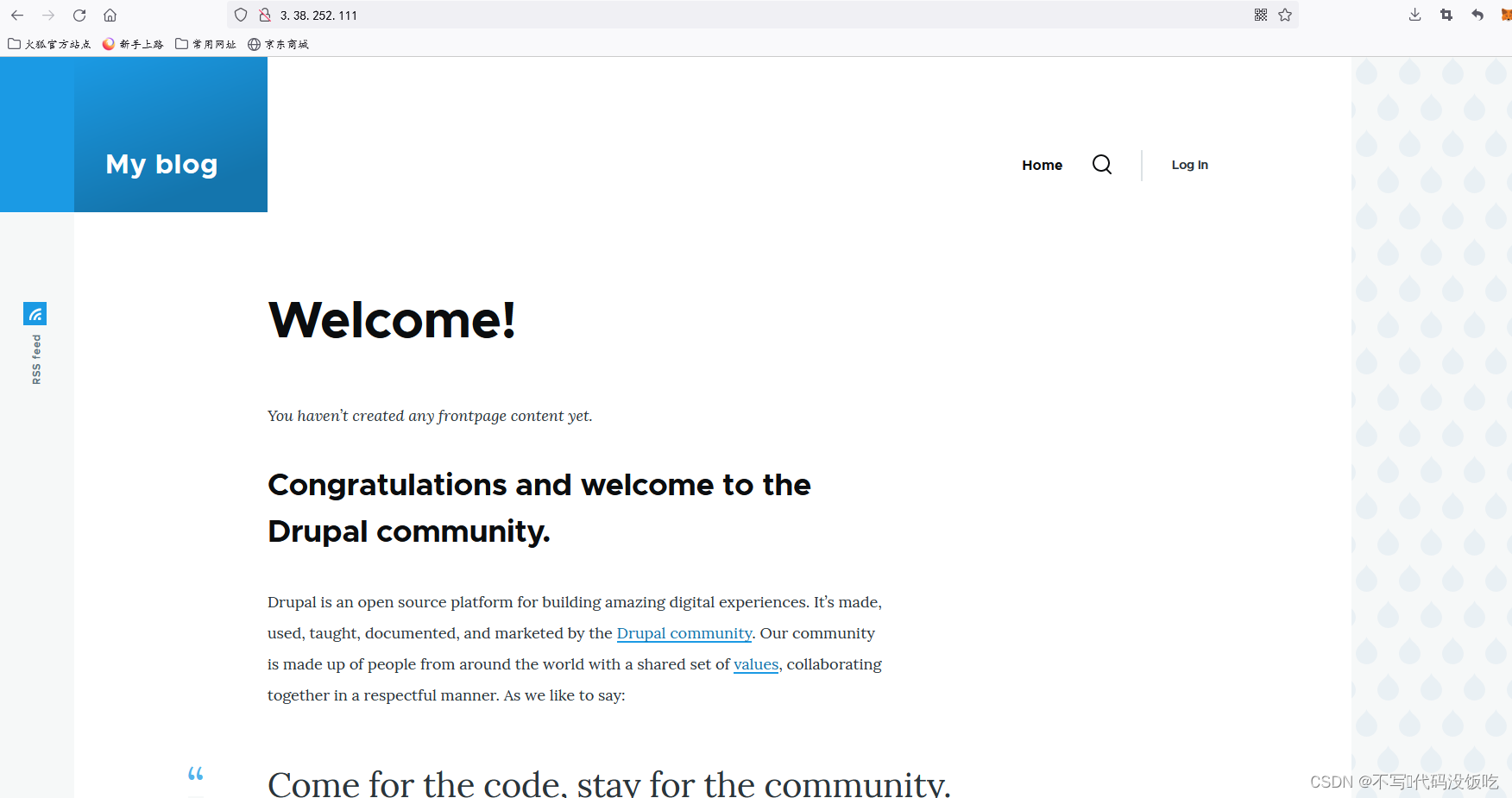
『亚马逊云科技产品测评』活动征文|通过lightsail一键搭建Drupal VS 手动部署
『亚马逊云科技产品测评』活动征文|通过lightsail一键搭建Drupal 提示:授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚…...

使用 VuePress 和 Vercel 打造个人技术博客:实现自动化部署
什么是VuePress? 以下是VuePress官方文档的介绍:VuePress 是一个以 Markdown 为中心的静态网站生成器。你可以使用 Markdown 来书写内容(如文档、博客等),然后 VuePress 会帮助你生成一个静态网站来展示它们。VuePress 诞生的初…...
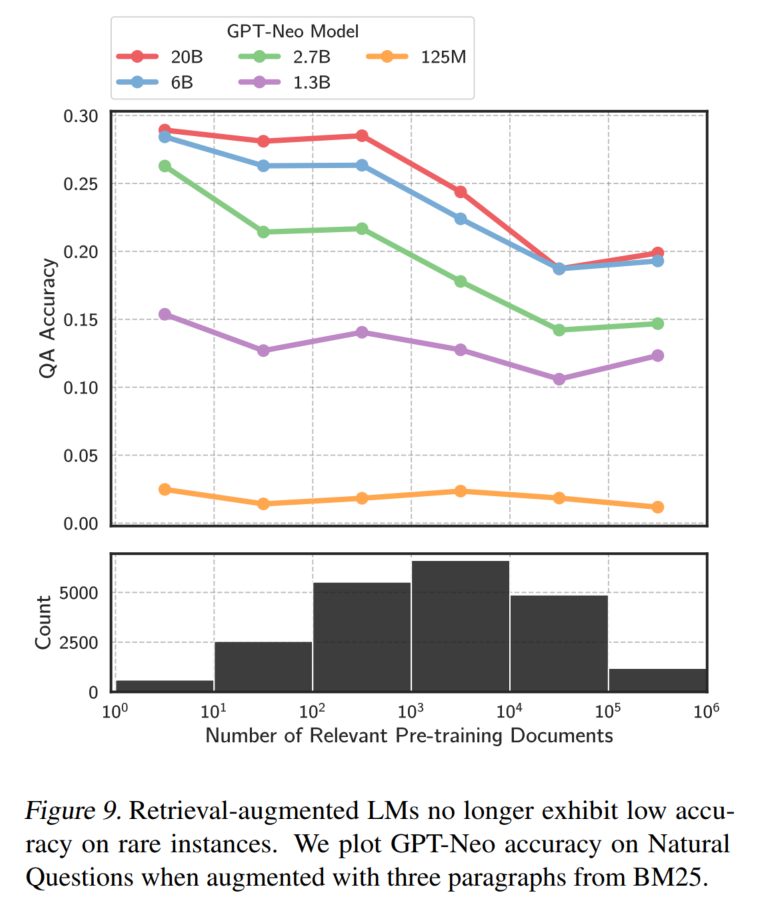
Re50:读论文 Large Language Models Struggle to Learn Long-Tail Knowledge
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文名称:Large Language Models Struggle to Learn Long-Tail Knowledge ArXiv网址:https://arxiv.org/abs/2211.08411 官方GitHub项目(代码和实体)…...
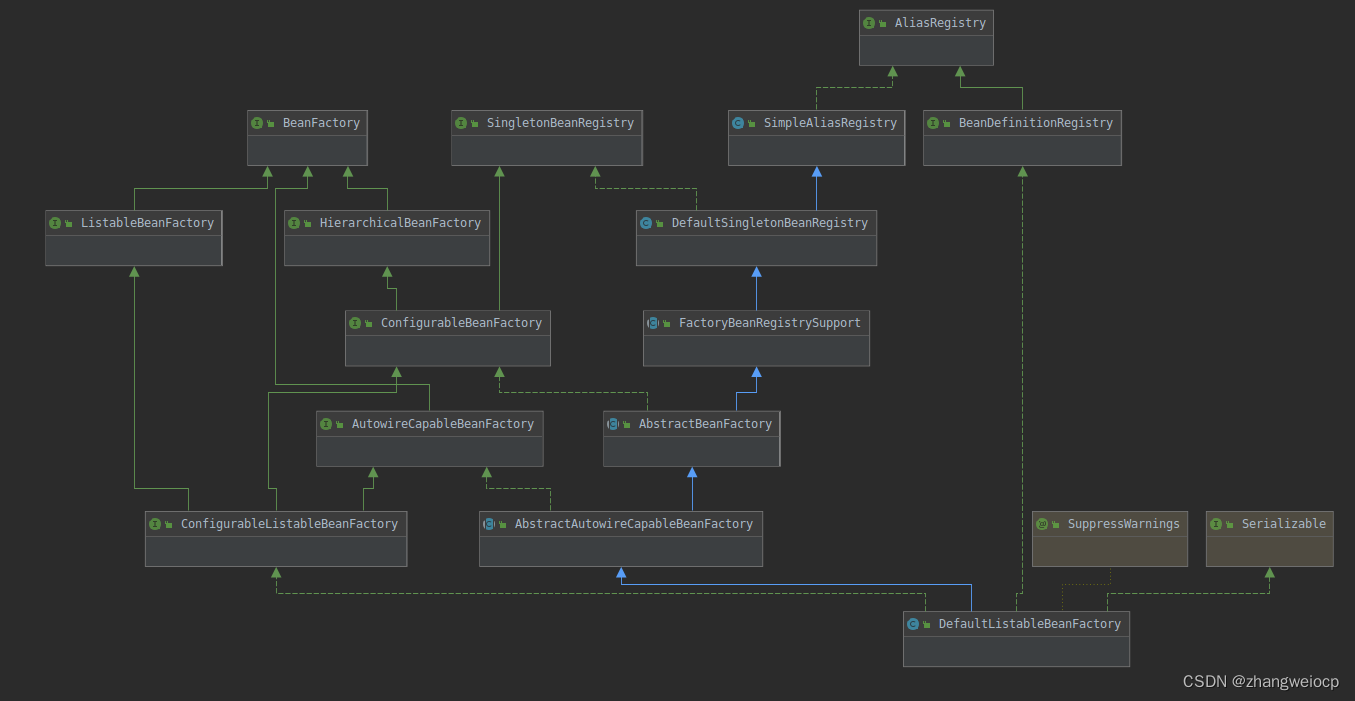
Spring IOC - Bean的生命周期之依赖注入
在Spring启动流程中,创建的factoryBean是DefaultListableBeanFactory,其类图如下所示: 可以看到其直接父类是AbstractAutoireCapableBeanFactory,他主要负责完成Bean的自动装配和创建工作。 具体来说,AbstractAutowire…...
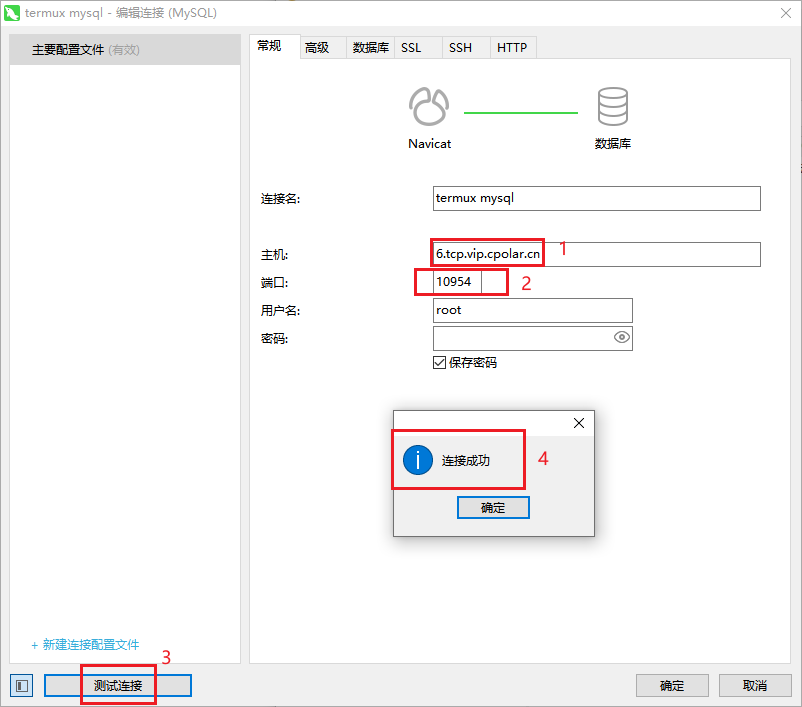
Android Termux安装MySQL,内网穿透实现公网远程访问
文章目录 前言1.安装MariaDB2.安装cpolar内网穿透工具3. 创建安全隧道映射mysql4. 公网远程连接5. 固定远程连接地址 前言 Android作为移动设备,尽管最初并非设计为服务器,但是随着技术的进步我们可以将Android配置为生产力工具,变成一个随身…...
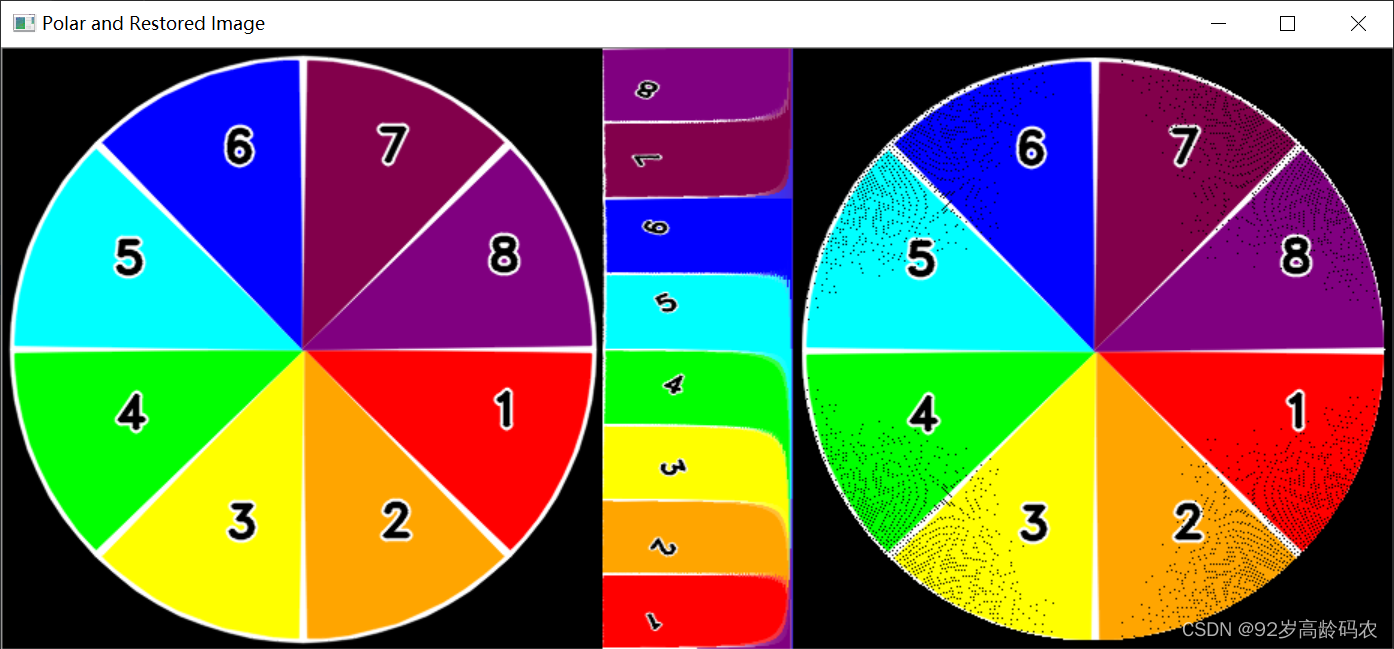
OpenCV快速入门:像素操作和图像变换
文章目录 前言1. 像素操作1.1 像素统计1.2 两个图像之间的操作1.2.1 图像加法操作1.2.3 图像加权混合 1.3 二值化1.4 LUT(查找表)1.4.1 查找表原理1.4.2 代码演示 2 图像变换2.1 旋转操作2.1.1 旋转的基本原理2.1.2 代码实现 2.2 缩放操作2.3 平移操作2.…...
Django 路由配置(二)
一、路由 就是根据用户请求的URL链接来判断对应的出来程序,并返回处理结果,也是就是URL和django的视图建立映射关系. 二、Django请求页面的步骤 1、首先Django确定要使用的根URLconf模块,通过ROOT_URLCONF来设置,在settings.py配置…...

电子学会C/C++编程等级考试2022年06月(一级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:倒序输出 依次输入4个整数a、b、c、d,将他们倒序输出,即依次输出d、c、b、a这4个数。 时间限制:1000 内存限制:65536输入 一行4个整数a、b、c、d,以空格分隔。 0 < a,b,c,d < 108输出 一行4个整数d、c、b、a,整数之…...
【C++】使用std::vector()函数实现矩阵的加、减、点乘、点除等运算
本文通过vector()函数表示矩阵的形式,对 加、减、点乘、点除等运算进行编码和运行,相应结果如下文所述。 #include <iostream> #include <vector>using namespace std;// 矩阵加法 vector<vector<int>> …...
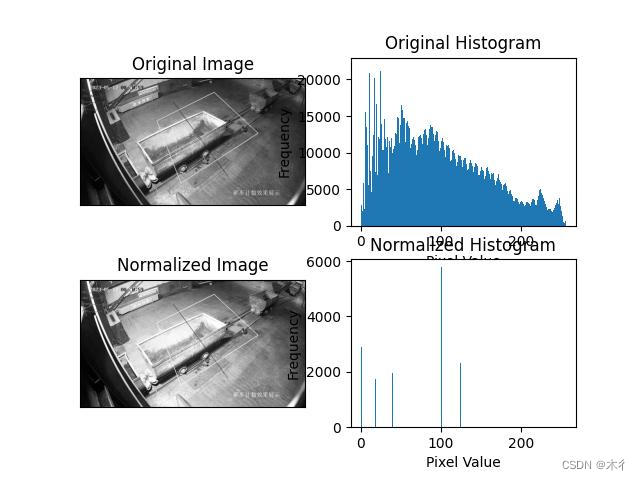
【python】直方图正则化详解和示例
直方图正则化(Histogram Normalization)是一种图像增强技术,目的是改变图像的直方图以改善图像的质量。具体来说,它通过将图像的直方图调整为指定的形状,以增强图像的对比度和亮度。 直方图正则化的基本步骤如下&…...

c语言:矩阵交换
题目: 代码和思路: #define _CRT_SECURE_NO_WARNINGS #include<stdio.h>int main() {int n 0;int m 0;int arr[10][10] { 0 }; // 输入行和列scanf("%d%d", &n, &m);int i 0;int j 0;//读取数组for (i 0; i < n; i)…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
