数据结构 并查集
作用
快速的处理以下问题:【近乎O(1)的时间完成】
1.将两个集合合并
2.询问两个元素是否在一个集合中
用树的形式维护集合
基本原理
每一个集合用一棵树表示
每一个集合的编号就是根结点的编号,对于每一个结点,都存储其父结点,p[x]表示x的父结点,即p[x]=a表示编号为x的结点的父结点的编号为a
求某个点属于哪个集合时,就先找其父结点,如果其父结点不是根结点,那么就继续找其父结点的父结点,直到找到其根结点为止
问题1
如何判断树根:if(p[x]==x)
问题2
如何求x的集合编号:while(p[x]!=x) x=p[x];【只要x不是树根,就一直往上走,直到找到树根为止】
该步骤时间复杂度仍然很高,需要进行以下优化:
路径压缩:一旦找到根结点,就会把整个路径上所有点都指向根结点。【基本O(1)】
安秩合并【一般不用】
问题3
如何合并两个集合:px是x集合的集合编号【即x集合的根节点的编号是px】,py是y集合的集合编号【即y集合的根节点的编号是py】 p[px]=py或p[py]=px
代码实现
int find(int x) {//返回x所在集合的编号+路径压缩
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
例题——合并集合
一共有n个数,编号是1~n,最开始每个数各自在一个集合中。
现在要进行m个操作,操作共有两种:
“M a b”,将编号为a和b的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
“Q a b”,询问编号为a和b的两个数是否在同一个集合中;
输入格式
第一行输入整数n和m。
接下来m行,每行包含一个操作指令,指令为“M a b”或“Q a b”中的一种。
输出格式
对于每个询问指令”Q a b”,都要输出一个结果,如果a和b在同一集合内,则输出“Yes”,否则输出“No”。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例
Yes
No
Yes
代码
#include<iostream>
using namespace std;
const int N = 100010;
int p[N];//存储父结点
int n, m;
int find(int x) {//返回x所在集合的编号+路径压缩
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++)
p[i] = i;
while (m--) {
char op[2];//因为在使用scanf进行读取时,若读取单个字符会读取到空格、回车等其他字符,使用scanf读取字符串时可忽略空格、回车等其他字符
int a, b;
scanf("%s%d%d", op, &a, &b);
if (op[0] == 'M')
p[find(a)] = find(b);//合并
//find(a)返回a的祖宗结点,find(b)返回b的祖宗结点,让a的祖宗结点的父结点等于b的祖宗结点
else {
if (find(a) == find(b))
puts("Yes");
else
puts("No");
}
}
return 0;
}
例题——连通块中点的数量
给定一个包含n个点(编号为1~n)的无向图,初始时图中没有边。
现在要进行m个操作,操作共有三种:
“C a b”,在点a和点b之间连一条边,a和b可能相等;
“Q1 a b”,询问点a和点b是否在同一个连通块中,a和b可能相等;
“Q2 a”,询问点a所在连通块中点的数量;
输入格式
第一行输入整数n和m。
接下来m行,每行包含一个操作指令,指令为“C a b”,“Q1 a b”或“Q2 a”中的一种。
输出格式
对于每个询问指令”Q1 a b”,如果a和b在同一个连通块中,则输出“Yes”,否则输出“No”。
对于每个询问指令“Q2 a”,输出一个整数表示点a所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤10^5
输入样例
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例
Yes
2
3
代码
#include<iostream>
using namespace std;
const int N = 100010;
int p[N], size1[N];//存储父结点
int n, m;
int find(int x) {//返回x所在集合的编号+路径压缩
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++) {
p[i] = i;
size1[i] = 1;
}
while (m--) {
char op[5];
int a, b;
scanf("%s", op);
if (op[0] == 'C') {
scanf("%d%d", &a, &b);
if (find(a) == find(b))
continue;
//特判:如果两个数已经在一个集合,就不用再次合并,不然会使得元素中的元素个数翻倍
size1[find(b)] += size1[find(a)];//b中元素数量为其本身加上a中元素数量
p[find(a)] = find(b);//合并,将a合并到b中
}
else if (op[1] == '1') {
scanf("%d%d", &a, &b);
if (find(a) == find(b))
puts("Yes");
else
puts("No");
}
else {
scanf("%d", &a);
printf("%d\n", size1[find(a)]);
}
}
return 0;
}
相关文章:

数据结构 并查集
作用 快速的处理以下问题:【近乎O(1)的时间完成】 1.将两个集合合并 2.询问两个元素是否在一个集合中 用树的形式维护集合 基本原理 每一个集合用一棵树表示 每一个集合的编号就是根结点的编号,对于每一个结点,都存储其父结点…...
)
算法通关村第十六关黄金挑战——求滑动窗口中的最大值(滑动窗口与堆方法、双端队列法和直接比较法)
大家好,我是怒码少年小码。 今天这篇就讲一道题目,不难😎,但是一定要学会自己思考。 滑动窗口最大值 LeetCode 239:给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。…...

常见树种(贵州省):009楠木、樟木、桂木种类
摘要:本专栏树种介绍图片来源于PPBC中国植物图像库(下附网址),本文整理仅做交流学习使用,同时便于查找,如有侵权请联系删除。 图片网址:PPBC中国植物图像库——最大的植物分类图片库 一、楠木 …...
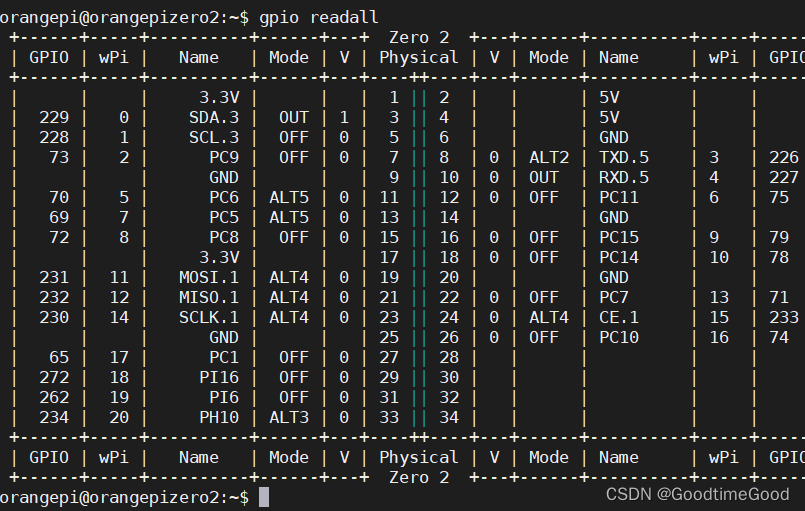
全志H616开发版
开发板介绍: 二、开发板刷机 SDFormatter TF卡的格式化工具、Win32Diskimager 刷机工具 刷机镜像为:Orangepizero2_2.2.0_ubuntu_bionic_desktop_linux4.9.170.img 使用MobaXterm_Personal_20.3连接使用 网络配置:nmcli dev wifi 命令接入网…...
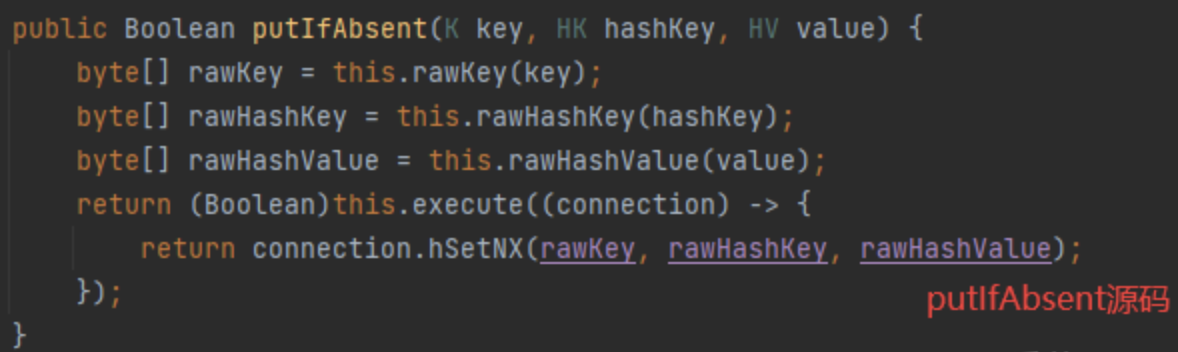
【Spring boot】RedisTemplate中String、Hash、List设置过期时间
文章目录 前言Redis中String设置时间的方法Redis中Hash和List设置时间的方法Redis中Hash的put、putAll、putIfAbsent区别 前言 时间类型:TimeUnit import java.util.concurrent.TimeUnit;TimeUnit.SECONDS:秒 TimeUnit.MINUTES:分 TimeUnit.HOURS&…...
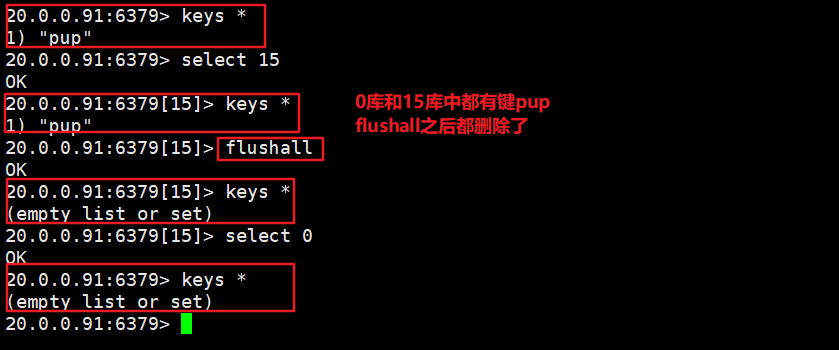
Nosql之redis概述及基本操作
关系数据库与非关系型数据库概述 关系型数据库 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一般面向于记录。SQL语句(标准数据查询语言)就是一种基于关系型数据库的语言,用于执行对关系型…...

使ros1和ros2的bag一直互通
很多文章都是先source ros1 然后source ros2,再play bag source /opt/ros/noetic/setup.bash source /opt/ros/foxy/setup.bash ros2 bag play -s rosbag_v2 kitti_raw00.bag 但实测会出问题: 为使ros1和ros2的bag一直互通 sudo apt update sudo apt install ros-foxy-ro…...

【正点原子 linux 驱动编程】
在此声明,正用点编的说明书真的拉,丝毫不具备兼容性。。比如linux的第一个实验,其中包含的 unregister_chrdev_region 函数,fileoperation 结构体等均来自 <linux/fs.h> 文件,搞不懂,他们方ide.h&…...

使用Python的turtle模块绘制玫瑰花图案(含详细Python代码与注释)
1.1引言 turtle模块是Python的标准库之一,它提供了一个绘图板,让我们可以在屏幕上绘制各种图形。通过使用turtle,我们可以创建花朵、叶子、复杂的图案等等。本博客将介绍如何使用turtle模块实现绘制图形的过程,并展示最终结果。 …...

Redis学习笔记14:基于spring data redis及lua脚本ZSET有序集合实现环形结构案例及lua脚本如何发送到redis服务器
案例实现目标,一、实现一个环形结构,环形结构上节点有一个阀值threshold,超过阀值则移除分数score最低的成员,不足则将当前成员添加进环中,且确保成员不可重复;二、每次访问环中的数据都需要刷新key的过期时间…...

openssl C++研发之pem格式处理详解
一、PEM_writeXXX和EM_write_bio_XXX 在OpenSSL的crypto/pem.h头文件中,PEM_write_XXXX和PEM_write_bio_XXXX系列函数用于将特定类型的数据写入文件或BIO(内存缓冲区)中,其中XXXX代表不同的数据类型。 这些函数的使用方式相似&a…...

【教3妹学编辑-mysql】详解数据库三大范式
什么是范式 简单地理解就是:数据库设计时遵循的规范 三大范式 数据库三大范式包含:1、第一范式(1NF);2、第二范式(2NF);3、第三范式(3NF)。其中,第一范式(1NF)的要求是属性不可分割,第二范式(2NF)的要求是…...

【计算机网络笔记】路由算法之链路状态路由算法
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...
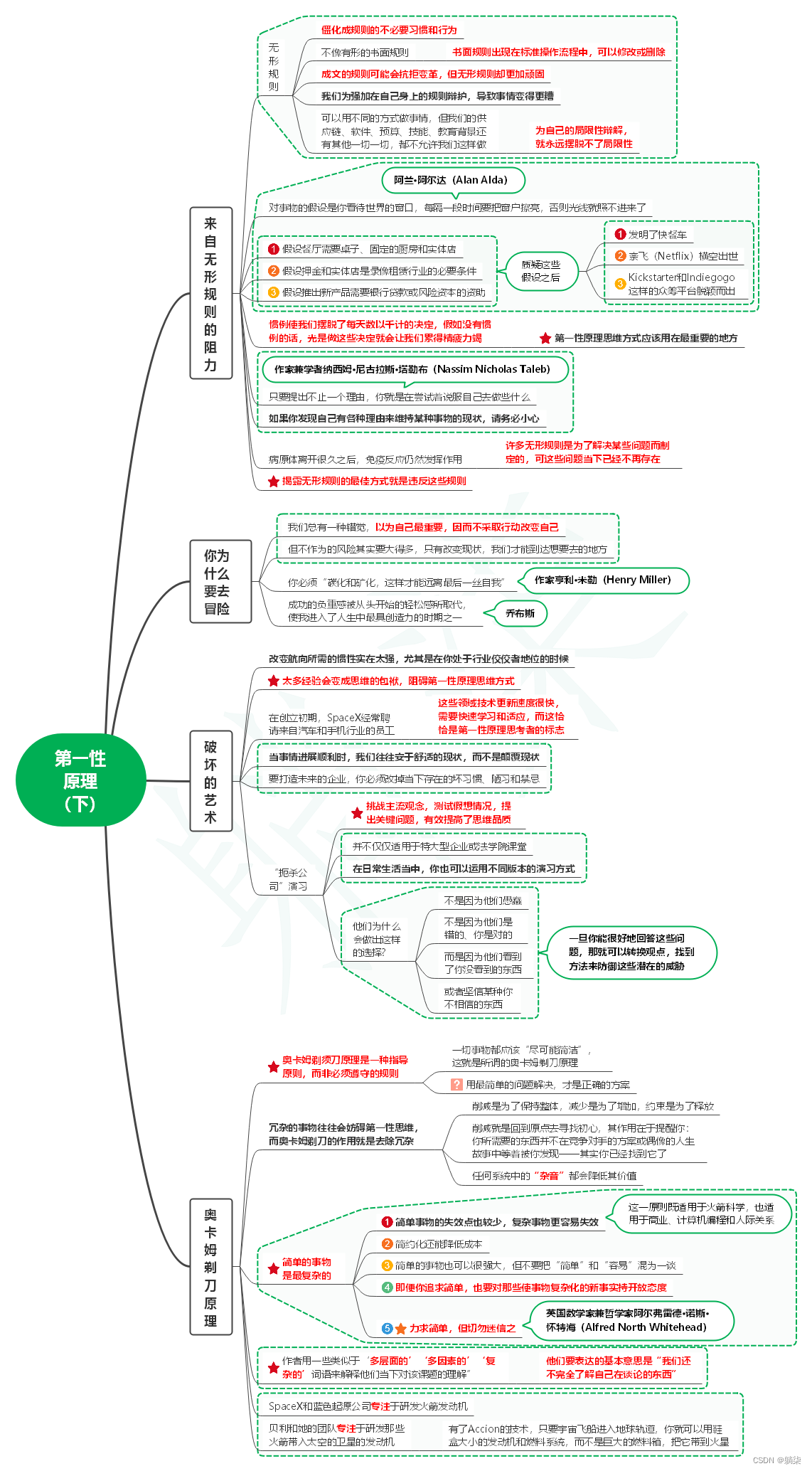
读像火箭科学家一样思考笔记04_第一性原理(下)
1. 来自无形规则的阻力 1.1. 无形规则 1.1.1. 僵化成规则的不必要习惯和行为 1.1.2. 不像有形的书面规则 1.1.2.1. 书面规则出现在标准操作流程中,可以修改或删除 1.1.3. 成文的规则可能会抗拒变革,但无形规则却更加顽固 1.1.4. 我们为强加在自己身…...

开源集群管理系统对比分析:Kubernetes 与 Apache Mesos
集群管理系统是关键的软件解决方案,可以在互连机器网络中有效分配和利用计算资源。毫无疑问,它们通过确保可扩展性、高可用性和有效的资源管理在现代计算中发挥着至关重要的作用,这使得它们对于运行复杂的应用程序、管理数据中心以及进一步增…...

matlab 坡度滤波算法地面分割
目录 一、算法原理1、实现流程2、参考文献二、代码实现三、结果展示四、测试数据一、算法原理 1、实现流程 1、格网示意图 2、计算格网行列数 公式中的特殊符号为向上取整,...

【腾讯云 HAI域探秘】高性能服务器引领AI革新浪潮:从AI绘画、知识问答到PyTorch图像分类、视频检测的全方位探索
目录 1 HAI(高性能应用服务)简介2 HAI的应用场景2.1 HAI在AI作画中的灵活性与效率2.2 深入探索LLM语言模型的应用与性能2.3 HAI支持的AI模型开发环境与工具 3 基于stable difussio的AI 绘画应用实践3.1 使用AI模型中的stable diffusion模型服务3.2 设置和…...
)
【Java】ExcelWriter自适应宽度工具类(支持中文)
工具类 import org.apache.poi.ss.usermodel.Cell; import org.apache.poi.ss.usermodel.CellType; import org.apache.poi.ss.usermodel.Row; import org.apache.poi.ss.usermodel.Sheet;/*** Excel工具类** author xiaoming* date 2023/11/17 10:40*/ public class ExcelUti…...

C++二分查找算法:132模式枚举3简洁版
本文涉及的基础知识点 二分查找算法合集 本题不同解法 包括题目及代码C二分查找算法:132 模式解法一枚举3C二分查找算法:132 模式解法二枚举2代码简洁C二分查找算法:132 模式解法三枚举1性能最佳C单调向量算法:132 模式解法三枚…...

Map 和 WeakMap:JavaScript 中的键值对集合
JavaScript 是一种动态、弱类型的脚本语言,经常用于构建现代 Web 应用程序。在编写 JavaScript 代码时,我们经常需要使用各种数据结构来存储和管理数据。其中,Map 和 WeakMap 就是两个非常有用的数据结构,它们分别提供了用于存储键…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
