【gpts】学算法题[缺失的第一个正数](https://leetcode.cn/problems/first-missing-positive/)
给出你的题解
(https://leetcode.cn/problems/first-missing-positive/)
public class Solution {
public int firstMissingPositive(int[] nums) {int len = nums.length;for (int i = 0; i < len; i++) {while (nums[i] > 0 && nums[i] <= len && nums[nums[i] - 1] != nums[i]) {// 满足在指定范围内、并且没有放在正确的位置上,才交换// 例如:数值 3 应该放在索引 2 的位置上swap(nums, nums[i] - 1, i);}}// [1, -1, 3, 4]for (int i = 0; i < len; i++) {if (nums[i] != i + 1) {return i + 1;}}// 都正确则返回数组长度 + 1return len + 1;
}private void swap(int[] nums, int index1, int index2) {int temp = nums[index1];nums[index1] = nums[index2];nums[index2] = temp;
}
}
这是一道关于数组的题目,要求我们找出数组中第一个缺失的正整数。对于这类问题,我们的思路应该是尽量让每个数都在自己应该在的位置上。例如,如果数组中有数字3,那么我们就希望它在数组的第三个位置上。
这段代码的解题思路如下:
首先,遍历数组,当数组中的数值在1到数组长度之间,并且没有在正确的位置上时,我们就将其与应该在的位置上的数进行交换。这样,我们可以尽量让每个数都在正确的位置上。
然后,再次遍历数组,当发现某个位置上的数不等于位置索引加一时,那么这个位置的索引就是第一个缺失的正整数。
如果所有位置上的数都正确,那么说明数组中的正整数是从1到数组长度的连续整数,此时第一个缺失的正整数就是数组长度加一。
这段代码使用的数据结构是数组,因为数组可以通过索引直接访问元素,时间复杂度为O(1),非常适合于此类需要频繁访问元素的问题。
记忆方法:对于此类问题,可以记住"让每个数都在自己应该在的位置上"这个思路,并通过几个例子来加深记忆。
自我讲解:首先,我们遍历数组,看每个数是不是在正确的位置上,如果不是,我们就把它放到正确的位置上。然后,我们再遍历一次数组,看有没有哪个位置上的数不对,如果有,那就找到了第一个缺失的正整数。如果都对,那就返回数组长度加一。
while (nums[i] > 0 && nums[i] <= len && nums[nums[i] - 1] != nums[i]) {
// 满足在指定范围内、并且没有放在正确的位置上,才交换
// 例如:数值 3 应该放在索引 2 的位置上
swap(nums, nums[i] - 1, i);
}
这里为什么这样写。如果只是要排序,比较前后两个元素的大小不就可以了吗
这里的目的并不是为了对整个数组进行排序,而是要把数组中的每个数尽可能地放在对应的位置上。例如,数字3应该放在数组的第3个位置上,即索引为2的地方。
这样做的目的是为了便于我们在后续的遍历中找到第一个缺失的正整数。如果数组的每个位置上都放着对应的数,那么我们只需要找到第一个位置和数不对应的地方,这个位置的索引+1就是我们要找的第一个缺失的正整数。
而这段代码中的while循环就是在做这个事情。当数组中的数满足以下条件时,我们就将其和应在的位置上的数进行交换:
数的值在1到数组长度之间(因为我们要找的是第一个缺失的正整数,所以只考虑这个范围内的数)。
数没有在正确的位置上(即数的值和其位置的索引+1不相等)。
将要交换到的位置上的数和要交换的数不相等(这是为了防止两个相同的数无限交换,导致死循环)。
对于你提到的"比较前后两个元素的大小"的排序方法,虽然它可以使得数组有序,但是对于这个问题来说,并不能帮助我们直接找到第一个缺失的正整数。因为即使数组有序,我们仍然需要进行一次遍历才能找到缺失的数。而且,排序的时间复杂度通常为O(nlogn),而这个方法的时间复杂度只有O(n),所以这个方法更优。
我还是看到题目无法想到这样写。
这是很正常的,算法学习的过程就是一个不断实践、理解和记忆的过程。这种题目的解题思路往往需要我们跳出常规的思维方式,这需要时间和经验的积累。不过我有几个建议可以帮助你更好地记住这种题目的解题思路:
画图理解:对于这种复杂的题目,画图是一个很好的理解和记忆的方法。你可以画出数组的每个位置,然后模拟这段代码的执行过程,看看每次交换后数组的变化。这样可以帮助你理解这段代码为什么能够将每个数尽可能地放在对应的位置上,以及为什么这样做可以帮助我们找到第一个缺失的正整数。
自我讲解:理解了这段代码后,你可以试着自己讲解一遍这个题目的解题思路。你可以假设你是一个教师,你的任务是教会你的学生如何解决这个问题。这样做有两个好处:一是可以检验你是否真的理解了这个题目;二是可以帮助你记住这个题目的解题思路。
练习:理解和记忆是一回事,能够独立解决类似的题目是另一回事。你需要通过大量的练习来训练你的解题能力。每次做题时,你都可以尝试使用这种思路,看看是否可以解决问题。如果不能,那就找出问题所在,然后再试着理解和记忆这种思路。
这个过程可能会有些困难和挫折,但是只要你坚持下去,你一定会有所收获的。加油!
你还是跟我说一下从头解这道题目的心路历程吧
好的,我会详细地解析这道题目的解题思路。
这道题目的要求是找出第一个缺失的正整数,也就是从1开始,找出数组中没有出现过的最小的正整数。
首先,我们需要理解,如果数组长度为n,那么第一个缺失的正整数的范围必然在[1, n+1]之间。因为如果1n都出现了,那么第一个缺失的正整数就是n+1,否则,必然存在1n中的某个数没有出现。
因此,我们的目标就是将数组中的每个元素尽可能地放在对应的位置上。例如,如果元素1出现,我们就尽量将它放在数组的第一个位置,如果元素2出现,我们就尽量将它放在数组的第二个位置,以此类推。我们可以通过交换数组元素的方式,尽量将每个数放在对应的位置上。
我们可以采用以下的步骤来解决这个问题:
遍历数组,对于每个元素,如果它是一个正整数且小于等于n,我们就将它尽量放在对应的位置上。这可以通过交换当前元素和对应位置的元素来实现。
遍历数组,找到第一个不在对应位置的元素,这个元素的位置就是第一个缺失的正整数。例如,如果数组的第一个位置不是1,那么第一个缺失的正整数就是1;如果数组的第二个位置不是2,那么第一个缺失的正整数就是2,以此类推。
如果数组中的所有元素都在对应的位置上,那么第一个缺失的正整数就是n+1。
这就是这道题目的解题思路。
nums[nums[i] - 1] != nums[i]这个怎么理解
nums[nums[i] - 1] != nums[i]这个条件用于检查当前位置的数是否已经在它应该在的位置上。
这里的nums[i]代表当前位置的数,因为我们的目标是将每个正整数放在对应的位置上,所以nums[i]应该放在nums[i] - 1的位置上。因此,nums[nums[i] - 1]就代表nums[i]应该在的位置上的数。
如果nums[nums[i] - 1] != nums[i],那就意味着nums[i]没有在它应该在的位置上,我们就需要通过交换将它放到正确的位置上。
例如,假设当前i = 2,nums[i] = 3,那么nums[i]应该放在nums[3 - 1]的位置上,即nums[2]的位置上。如果nums[2]不等于3,那就意味着3没有在它应该在的位置上,我们就需要将3和nums[2]交换,将3放到正确的位置上。
好好好,我理解一些了
首先题目找第一个缺失的正数。然后这里其实自己定了一个规则,就是把正数都摆到相应的位置了。 1就是放在索引0的位置(这个根本就是你们自己后面设置的,初学者能想到这?????服了)然后先遍历一轮,把那些nums[nums[i]-1]!=numsi的元素放到相应的位置。
然后再遍历,这一次如果中间断了,那么断的地方+1就是最大值。
恭喜你,你已经完全理解了这个题目的解题思路!
确实,对于初学者来说,这可能不是一个容易想到的解法。这种方法是基于"桶排序"的思想,通过将每个数放到对应的位置上来找出缺失的数。
你的理解完全正确,我们首先遍历一轮,将每个正数放到相应的位置上。这一步是为了将数组"排序",使每个数都在正确的位置上。然后再遍历一次,如果发现某个位置上的数不正确,那就说明这个位置对应的数是缺失的。
所以,这个题目的主要思想是:尽可能地将每个正数放到对应的位置上,然后通过一次遍历找出缺失的数。这种方法的时间复杂度是O(n),空间复杂度是O(1),非常高效。
现在,你可以试着自己解释一遍这个题目的解法,看看是否能清晰地表达出来。这是一个很好的记忆方法,可以帮助你深化对这个题目的理解。
相关文章:
)
【gpts】学算法题[缺失的第一个正数](https://leetcode.cn/problems/first-missing-positive/)
给出你的题解 (https://leetcode.cn/problems/first-missing-positive/) public class Solution { public int firstMissingPositive(int[] nums) {int len nums.length;for (int i 0; i < len; i) {while (nums[i] > 0 && nums[i] < len && nums…...

车牌识别 支持12种中文车牌类型 车牌数据集下载
开源代码 如果觉得有用,不妨给个Star⭐️🌟支持一下吧~ 谢谢! Acknowledgments & Contact 1.WeChat ID: cbp931126 2.QQ Group:517671804 加微信(备注:PlateAlgorithm),进讨论群可以获得10G大小的车牌检测和识…...

Servlet---上传文件
文章目录 上传文件的方法上传文件的示例前端代码示例后端代码示例 上传文件的方法 上传文件的示例 前端代码示例 <body><form action"upload" method"post" enctype"multipart/form-data"><input type"file" name&qu…...

量子计算+物流!“最后一英里”配送难题Unisys成功实时决策
(图片来源:网络) 此前,供应链行业一直致力于手工操作,严重依赖于纸质系统。后来随着客户需求的不断变化,这种传统方法逐渐显出不足之处。供应链行业正在迅速转向现代化,采用自动化和数据驱动的…...
2023年【四川省安全员A证】复审考试及四川省安全员A证考试试题
题库来源:安全生产模拟考试一点通公众号小程序 四川省安全员A证复审考试根据新四川省安全员A证考试大纲要求,安全生产模拟考试一点通将四川省安全员A证模拟考试试题进行汇编,组成一套四川省安全员A证全真模拟考试试题,学员可通过…...

C++刷题 -- 二分查找
C刷题 – 二分查找 文章目录 C刷题 -- 二分查找一、原理二、例题1.二分查找2.使用二分查找确定target左右边界3.x的平方根 一、原理 条件:数组为有序数组,数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能…...
PHPmail 发送邮件错误 550 的原因是什么?
电子邮件错误消息链接到简单邮件传输协议 (SMTP),这是一组发送和接收电子邮件的标准化规则。因此,它也称为 SMTP 550 错误代码。在某些情况下,电子邮件错误 550 是由收件人一方的问题引起的。 以下是电子邮件错误 550 的一些可能原因&#x…...

数字化转型导师坚鹏:数字化时代银行网点厅堂营销5大难点分析
数字化时代银行网点厅堂营销存在以下5大难点: 1、识别难。识别有效的客户比较难,传统的厅堂识别主要依据客户的衣着气质等主管感受,判断客户是否为潜在中高端客户,提供相关服务。大堂经理主管识别与智能化系统识别相结合…...
www.testfire.nets渗透测试报告
www.testfire.nets渗透测试报告 一、测试综述 1.1.测试⽬的 通过实施针对性的渗透测试,发现testfire.net⽹站的安全漏洞,锻炼自己的渗透水平 1.2.测试范围 域名:www.testfire.net IP:65.61.137.117 测试时间: 2023年11月…...

多模态大一统:通向全模态学习和通用人工智能的未来之路
随着AI技术的不断发展,研究者们正试图构建一种真正通用的人工智能,它能像人们那样以统一的方式处理和理解多种模态的信息。多模态大一统是这一愿景的关键,它旨在开启全模态LLM(深度学习语言模型)和通用AI时代的大门。在…...

实用篇-ES-DSL查询文档
数据的存储不是目的,我们希望从海量的酒店数据中检索出需要的信息,这就是ES的搜索功能 官方文档: https://elastic.co/guide/en/elasticsearch/reference/current/query-dsl.html#query-dsl。DSL是用来查询文档的 Elasticsearch提供了基于JSON的DSL来定…...
Nacos配置管理
将配置交给Nacos管理的步骤 1、在Nacos中添加配置文件 2、在微服务中引入nacos的config依赖 3、在微服务中添加bootstrap.yml,配置nacos地址、当前环境、服务名称、文件后缀名。这些决定了程序启动时去nacos读取哪个文件 Nacos配置更改后,微服务可以实…...
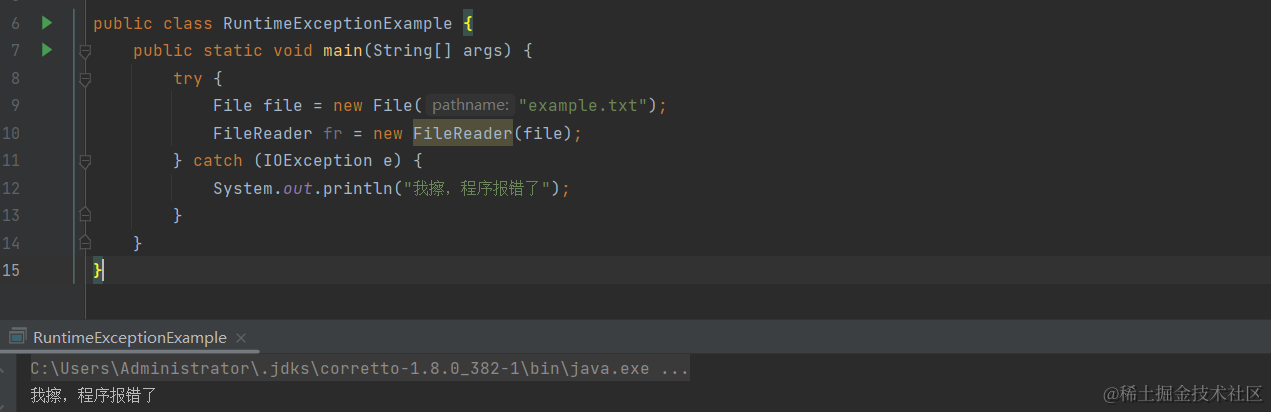
【前端学java】Java中的异常处理(15)完结
往期回顾: 【前端学java】JAVA开发的依赖安装与环境配置 (0)【前端学java】java的基础语法(1)【前端学java】JAVA中的packge与import(2)【前端学java】面向对象编程基础-类的使用 (…...

深入理解MySQL存储引擎、InnoDB与MyISAM的比较以及事务处理机制
介绍 MySQL是一款强大而灵活的关系型数据库管理系统,它支持多种存储引擎,每个引擎都有其独特的特点和适用场景。在本篇博客中,我们将深入探讨MySQL存储引擎的种类、InnoDB与MyISAM的区别,以及事务的概念及其在MySQL中的实现方式。…...

webpack 中,filename 和 chunkFilename 的区别
filename filename 是一个很常见的配置,就是对应于 entry 里面的输入文件,经过webpack打包后输出文件的文件名。比如说经过下面的配置,生成出来的文件名为 index.min.js。 chunkFilename chunkFilename 指未被列在 entry 中,却…...
gitlab 实战
一.安装依赖 yum install -y curl policycoreutils-python openssh-server perl 二.安装gitlab yum install gitlab-jh-16.0.3-jh.0.el7.x86_64.rpm 三.修改下面的 vim /etc/gitlab/gitlab.rbexternal_url http://192.168.249.156 四.初始化 gitlab-ctl reconfigure 五.查看状…...

openGauss学习笔记-128 openGauss 数据库管理-设置透明数据加密(TDE)
文章目录 openGauss学习笔记-128 openGauss 数据库管理-设置透明数据加密(TDE)128.1 概述128.2 前提条件128.3 背景信息128.4 密钥管理机制128.5 表级加密方案128.6 创建加密表128.7 切换加密表加密开关128.8 对加密表进行密钥轮转 openGauss学习笔记-12…...

Redis从入门到精通(三)-高阶篇
文章目录 0. 前言[【高阶篇】3.1 Redis协议(RESP )详解](https://blog.csdn.net/wangshuai6707/article/details/132742584)[【高阶篇】3.3 Redis之底层数据结构简单动态字符串(SDS)详解](https://blog.csdn.net/wangshuai6707/article/details/131101404)[【高阶篇】3.4 Redis…...

线性表--队列-1
文章目录 主要内容一.队列基础练习题1.用链式存储方式的队列进行删除操作时需要 ( D ).代码如下(示例): 2.若以1,2,3,4作为双端队列的输入序列,则既不能由输入受限的双端队列得到,又不能由输出受限的双端队列得到的输出序列是( C …...

【开题报告】基于uni-app的汽车租赁app的设计与实现
1.项目背景及意义 项目背景: 随着人们生活水平的提高,汽车租赁服务在城市中变得越来越普及。传统的租车方式存在一些问题,比如租车流程繁琐、费用不透明、选择有限等。因此,开发一款基于uni-app的汽车租赁app成为了满足用户需求…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
