3.查找算法:顺序查找和二分查找
查找
查找,是指在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程。
列表查找(线性表查找):从列表中查找指定元素
输入:列表,待查找元素
输出:元素下标(未查找到元素时返回-1)
顺序查找(线性查找)
顺序查找(linear search)
也叫线性查找(linear search),从列表的第一个元素开始,顺序的进行查找,直到找到元素或搜索到列表的最后一个元素为止。
代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>#define ARR_SIZE 10int linear_search(const int *arr, const int n, const int val)
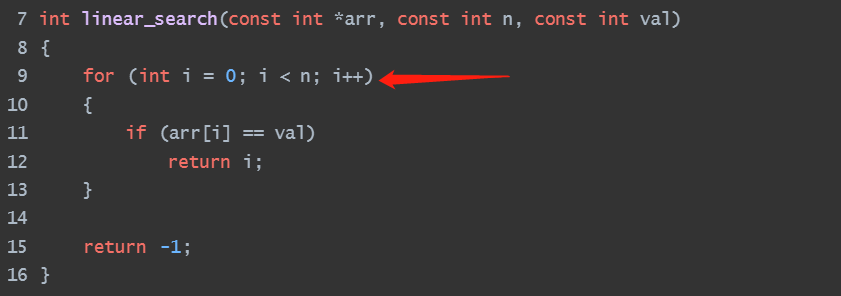
{for (int i = 0; i < n; i++){if (arr[i] == val)return i;}return -1;
}int main(int argc, char *argv[])
{srand(time(NULL));int arr[ARR_SIZE] = {0};printf("arr = "); for (int i = 0; i < ARR_SIZE; i++){arr[i] = rand()%10 + 1;printf("%d ", arr[i]);}printf("\n");int val = rand()%10 + 1;printf("search val = %d\n", val);int index = linear_search(arr, ARR_SIZE, val);printf("index = %d\n", index);return 0;
}结果:
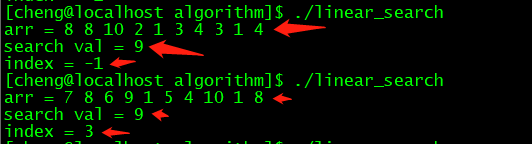
时间复杂度:O(n)
顺序查找算法最差的情况,需要循环n次,所以该算法的时间复杂度为O(n)
二分查找法
二分查找法(binary)
又叫折半查找,从有序的列表初始选区[0 n-1]开始,即下标left = 0,right = n - 1,通过待查找的值与候选区中间(即下标为mid)的值继续比较。可以使候选区减少一半。
代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>#define ARR_SIZE 10int binary_search(const int *arr, const int n, const int val)
{int left = 0;int right = n-1;int mid;while (left <= right){mid = (left + right)/2;if (arr[mid] == val) return mid;else if (arr[mid] > val) //候选区在leftright = mid - 1;else //候选区在rightleft = mid + 1;}return -1;
}int main(int argc, char *argv[])
{srand(time(NULL));int arr[ARR_SIZE] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};printf("arr = "); for (int i = 0; i < ARR_SIZE; i++)printf("%d ", arr[i]);printf("\n");int val = rand()%10 + 1;printf("search val = %d\n", val);int index = binary_search(arr, ARR_SIZE, val);printf("index = %d\n", index);return 0;
}结果:
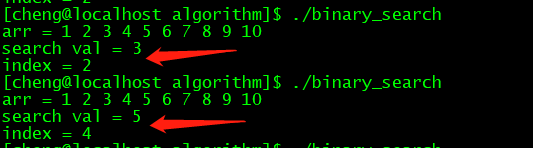
时间复杂度:
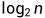 ,或logn
,或logn
二分查找算法,每次执行可以使候选区减少一半,所以时间复杂度为: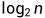 或logn
或logn
顺序查找和二分查找比较
通过以上分析,顺序查找的算法时间复杂度为:O(n),二分查找的算法时间复杂度为: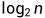
如果需要查找时,并且被查找的列表有序,那么选择二分查找,执行效率会比顺序查找快很多。
如果需要查找时,被查找的列表无序,就选择顺序查找。但是,如果需要频繁查找时,我们可以选择先对被查找的列表进行排序,然后在选择二分查找,从而提高查找的效率。
ending😃
相关文章:
3.查找算法:顺序查找和二分查找
查找查找,是指在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程。列表查找(线性表查找):从列表中查找指定元素输入:列表,待查找元素输出:元素下标(…...
攻不下dfs不参加比赛(七)
标题 为什么练dfs题目总结重点为什么练dfs 相信学过数据结构的朋友都知道dfs(深度优先搜索)是里面相当重要的一种搜索算法,可能直接说大家感受不到有条件的大家可以去看看一些算法比赛。这些比赛中每一届或多或少都会牵扯到dfs,可能提到dfs大家都知道但是我们为了避免眼高手…...

精确光度预测计算工具:AGi32 Crack
什么是AGi32? AGi32首先是一种用于精确光度预测的计算工具:一种技术工具,可以计算任何情况下的照度,协助灯具放置和瞄准,并验证是否符合任意数量的照明标准。 然而,要增强对光度学结果的理解,还…...
47个SQL性能优化技巧,看到就是赚到
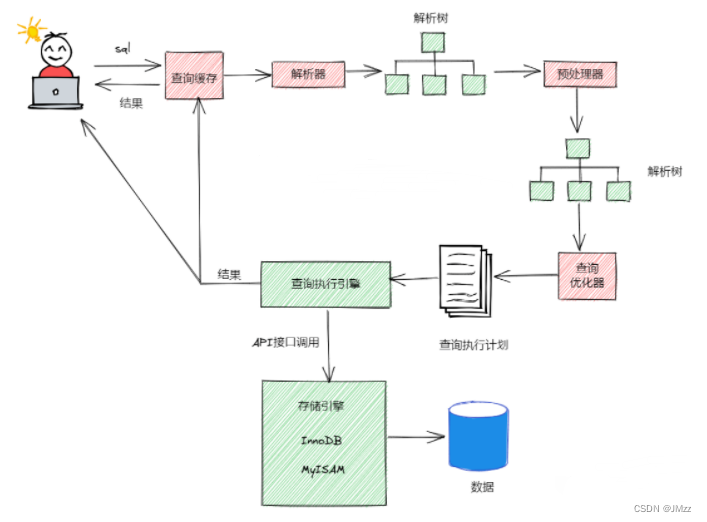
1、先了解MySQL的执行过程 了解了MySQL的执行过程,我们才知道如何进行sql优化。 (1)客户端发送一条查询语句到服务器; (2)服务器先查询缓存,如果命中缓存,则立即返回存储在缓存中的…...
汇川SV660N与基恩士 KV7500 控制器调试说明
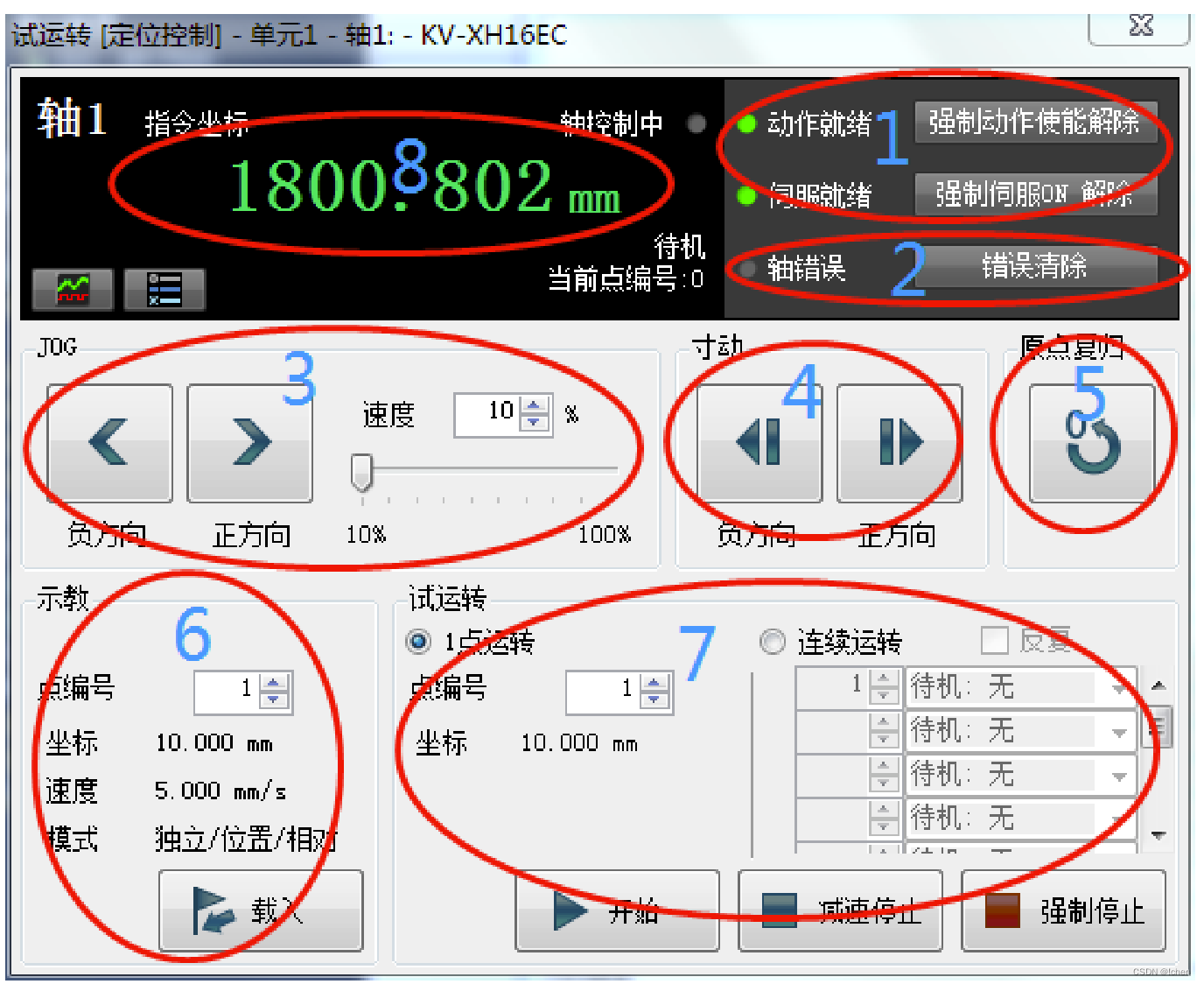
1. 伺服相关部分配置 1.1 伺服相关版本 SV660N 试机建议使用“SV660N-Ecat_v0.09.xml”及以上设备描述文件。 SV660N 单板软件版本建议为“H0100901.4”及更高版本号。 1.2 相关参数说明 SV660N 对象字典中 60FD 的含义较 IS620N 有所更改:bit0、1、2 分别为负限位…...

图观 | ChatGTP是如何通过知识图谱回答问题的?
文/Emma Z1950年,图灵发表了具有里程碑意义的论文《计算机器与智能》(Computing Machinery and Intelligence),提出了一个关于机器人的著名判断原则——图灵测试,也被称为图灵判断,它指出如果第三者无法辨别…...
Mysql的索引
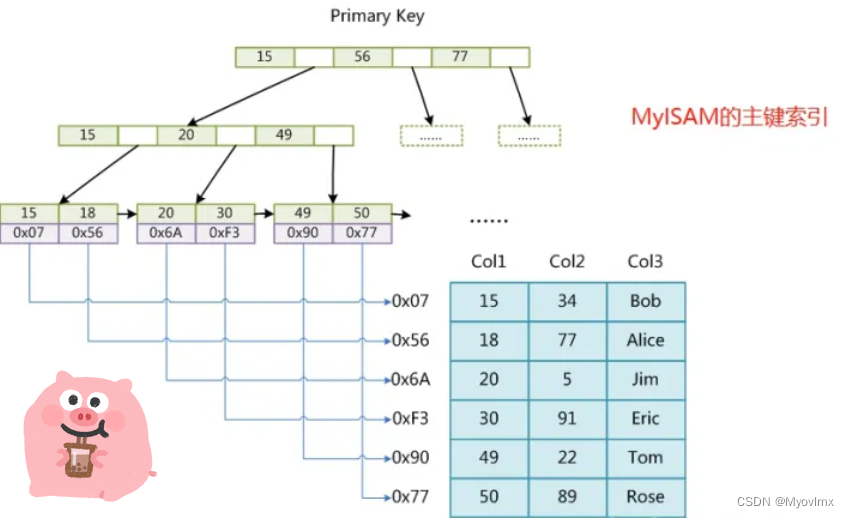
为什么写这篇文章呢~最近在梳理公司的数据库,在查看表结构的时候发现了这个 CREATE TABLE esp_5_N (ID int(11) NOT NULL AUTO_INCREMENT,pId int(11) DEFAULT NULL,EsFileId varchar(32) DEFAULT NULL,obligate1 varchar(45) DEFAULT NULL,obligate2 varchar(45) …...

计算机的发展
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。个人爱好: 编程,打篮球,计算机知识个人名言:海不辞水,故能成其大;山不辞石…...

理解Spring中的依赖注入和控制反转
依赖注入(Dependency Injection)是一种面向对象编程的设计模式,用于解决对象之间的依赖关系。它的基本思想是将对象的创建和管理工作交给容器来完成,而不是在应用程序中手动创建和管理对象,从而达到松耦合、易维护、易…...
XXL-JOB
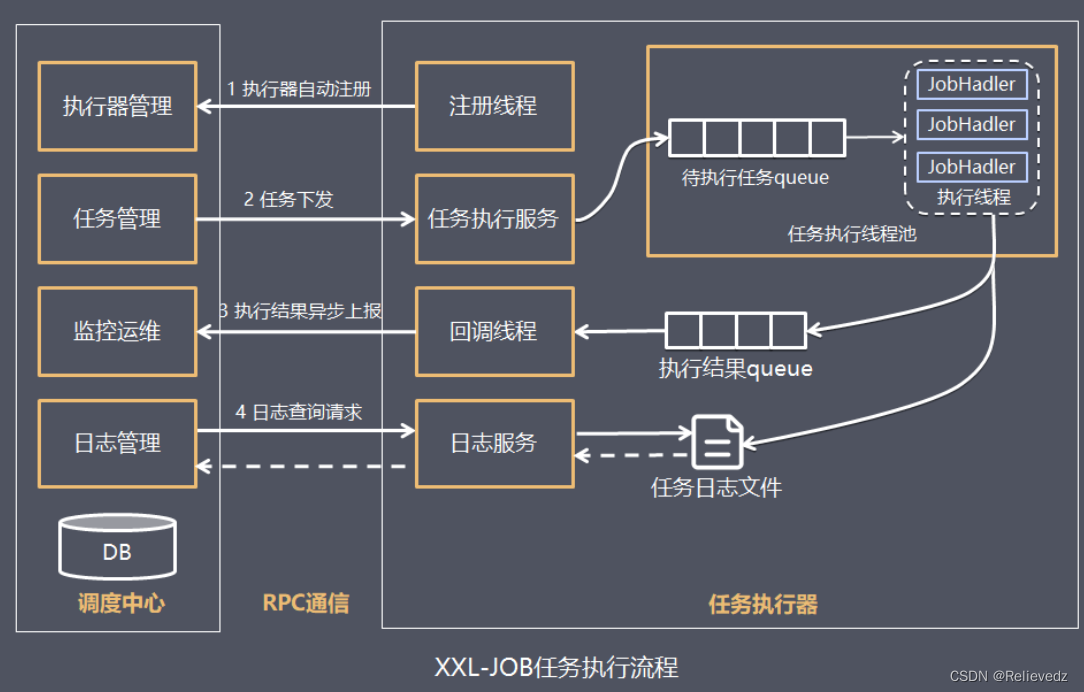
XXL-JOB介绍 XXL-JOB是一个轻量级分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品线,开箱即用。 官网:https://www.xuxueli.com/xxl-job/ 文档:分布式任务调度…...

「牛客网C」初学者入门训练BC134,BC136
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

华为OD机试题【翻转单词顺序】用 C++ 进行编码 (2023.Q1)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明翻转单…...
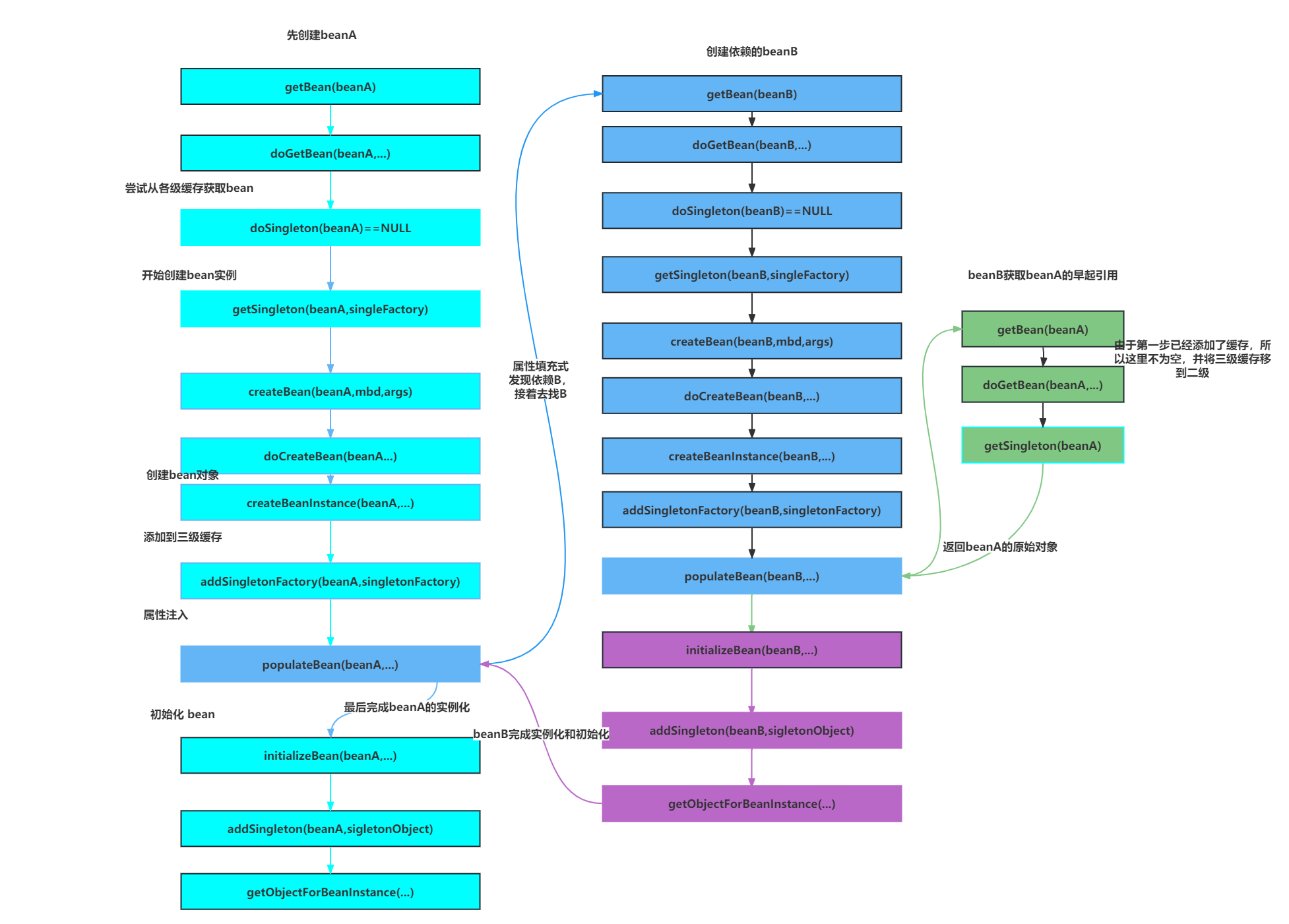
4.Spring【Java面试第三季】
4.Spring【Java面试第三季】前言推荐4.Spring27_Aop的题目说明要求Spring的AOP顺序AOP常用注解面试题28_spring4下的aop测试案例业务类新建一个切面类MyAspect并为切面类新增两个注解:spring4springboot1.5.9pom测试类29_spring4下的aop测试结果aop正常顺序异常顺序…...

ZLibrary使用说明-Zlirbrary
ZLibrary使用说明如果您是一位书虫,那么ZLibrary是一个值得一试的网站。该网站提供了大量的免费电子书籍,涵盖了各种不同的主题和类别。下面是一些有关如何使用ZLibrary的详细说明:第1步:访问ZLibrary网站要使用ZLibraryÿ…...
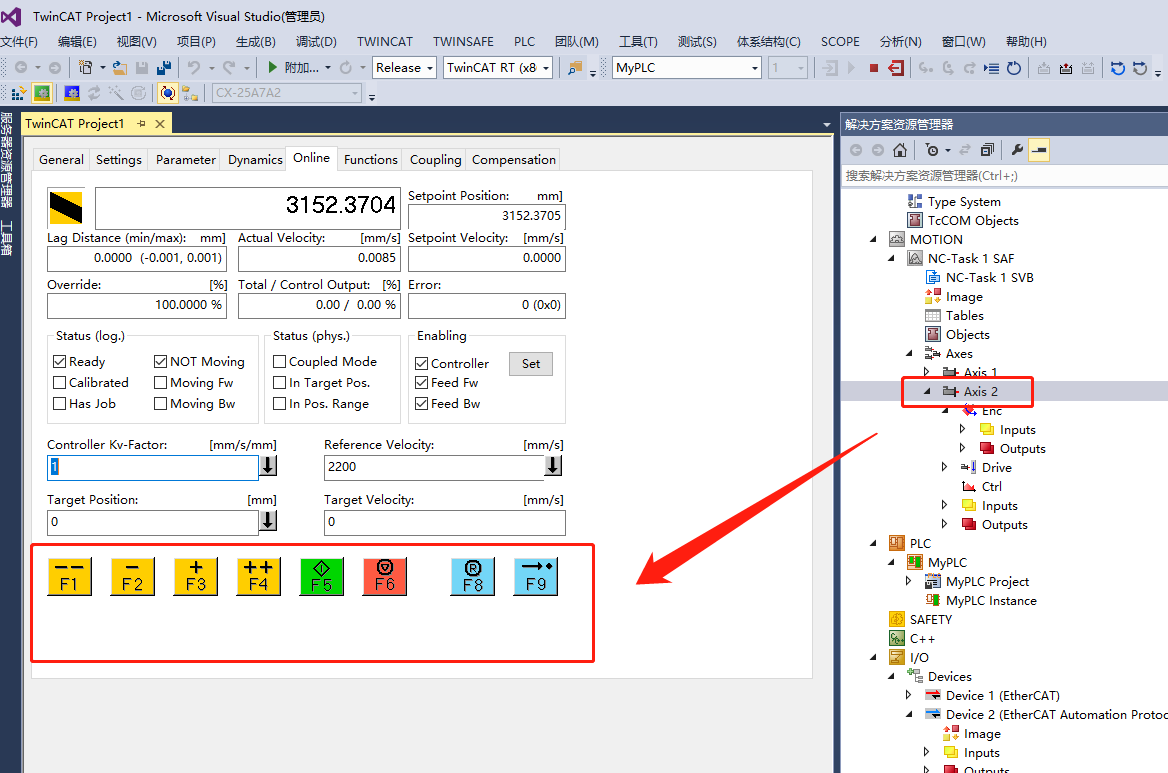
TwinCAT3第三方伺服电机——汇川SV660N使用
目录 一、第三方伺服在TC3中配置和使用 二、xml文件拷贝 编辑 三、IO中扫描伺服 四、工程测试 五、汇川伺服参数设置说明 一、第三方伺服在TC3中配置和使用 在倍福控制系统中使用第三方伺服可以参见本人另一篇博客,有详细教程说明。本文仅仅对SV660N伺服设置…...

进制转换(二进制,八进制,十进制,十六进制)涵盖整数与小数部分,内容的图片全为手写【详细图解】
各种进制之间的相互转换1. 各进制表示数1.1 数码1.2 基数1.3 位权2. 十进制转换为其他进制2.1 整数部分2.2 小数部分3. 其他进制转换为十进制4. 二进制转换为八进制5. 二进制转换为十六进制6. 八进制转换为十六进制1. 各进制表示数 二进制:0,1逢二进一 八…...
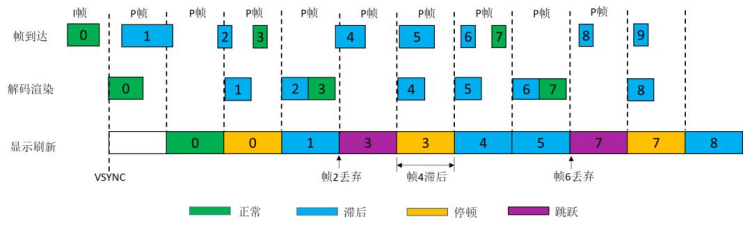
谈谈XR关键技术及VR/AR/MR/XR关系
一、先别被VR/AR/MR/XR搞晕,说说区别虚拟现实(Virtual Reality,VR)、增强现实(Augmented Reality,AR)等业务以其三维化、自然交互、空间计算等完全不同于当前移动互联网的特性,被认为…...
acwing1562 微博转发(宽搜)
微博被称为中文版的 Twitter。 微博上的用户既可能有很多关注者,也可能关注很多其他用户。 因此,形成了一种基于这些关注关系的社交网络。 当用户在微博上发布帖子时,他/她的所有关注者都可以查看并转发他/她的帖子,然后这些人…...

如何使用Arsenal快速部署功能强大的Bug Bounty工具
关于Arsenal Arsenal是一个功能强大且使用简单的Shell脚本(Bash),该工具专为漏洞赏金猎人设计,在该工具的帮助下,我们可以轻松在自己环境中安装并部署目前社区中功能最为强大的网络侦查工具、漏洞扫描工具和其他安全研…...
python网络爬虫(理论+实战)——正则表达式再讨论、常用正则表达式整理)
(十)python网络爬虫(理论+实战)——正则表达式再讨论、常用正则表达式整理
系列文章目录 (1)python网络爬虫—快速入门(理论+实战)(一) (2)python网络爬虫—快速入门(理论+实战)(二) (3) python网络爬虫—快速入门(理论+实战)(三) (4)python网络爬虫—快速入门(理论+实战)(四) (5)...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...
