python数据结构与算法-10_递归
递归
Recursion is a process for solving problems by subdividing a larger
problem into smaller cases of the problem itself and then solving
the smaller, more trivial parts.
递归是计算机科学里出现非常多的一个概念,有时候用递归解决问题看起来非常简单优雅。
之前讲过的数据结构中我们并没有使用递归,因为递归涉及到调用栈,可能会让初学者搞晕。这一章我们开始介绍递归,
后边讲到树和一些排序算法的时候我们还会碰到它。我非常推荐你先看看《算法图解》第三章 递归,
举的例子比较浅显易懂。
什么是递归?
递归用一种通俗的话来说就是自己调用自己,但是需要分解它的参数,让它解决一个更小一点的问题,当问题小到一定规模的时候,需要一个递归出口返回。
这里举一个和其他很多老套的教科书一样喜欢举的例子,阶乘函数,我觉得用来它演示再直观不过。它的定义是这样的:

我们很容易根据它的定义写出这样一个递归函数,因为它本身就是递归定义的。
def fact(n):if n == 0:return 1else:return n * fact(n-1)
看吧,几乎完全是按照定义来写的。我们来看下递归函数的几个特点:
- 递归必须包含一个基本的出口(base case),否则就会无限递归,最终导致栈溢出。比如这里就是 n == 0 返回 1
- 递归必须包含一个可以分解的问题(recursive case)。 要想求得 fact(n),就需要用 n * fact(n-1)
- 递归必须必须要向着递归出口靠近(toward the base case)。 这里每次递归调用都会 n-1,向着递归出口 n == 0 靠近
调用栈
看了上一个例子你可能觉得递归好简单,先别着急,我们再举个简单的例子,上边我们并没有讲递归如何工作的。
假如让你输出从 1 到 10 这十个数字,如果你是个正常人的话,我想你的第一反应都是这么写:
def print_num(n):for i in range(1, n + 1): # 注意很多编程语言使用的都是 从 0 开始的左闭右开区间, python 也不例外print(i)if __name__ == '__main__':print_num(10)
我们尝试写一个递归版本,不就是自己调用自己嘛:
def print_num_recursive(n):if n > 0:print_num_recursive(n-1)print(n)
你猜下它的输出?然后我们调换下 print 顺序,你再猜下它的输出
def print_num_recursive_revserve(n):if n > 0:print(n)print_num_recursive_revserve(n-1)
你能明白是为什么吗?我建议你运行下这几个小例子,它们很简单但是却能说明问题。
计算机内部使用调用栈来实现递归,这里的栈一方面指的是内存中的栈区,一方面栈又是之前讲到的后进先出这种数据结构。
每当进入递归函数的时候,系统都会为当前函数开辟内存保存当前变量值等信息,每个调用栈之间的数据互不影响,新调用的函数
入栈的时候会放在栈顶。视频里我们会画图来演示这个过程。
递归只用大脑不用纸笔模拟的话很容易晕,因为明明是同一个变量名字,但是在不同的调用栈里它是不同的值,所以我建议
你最好手动画画这个过程。

用栈模拟递归
刚才说到了调用栈,我们就用栈来模拟一把。之前栈这一章我们讲了如何自己实现栈,不过这里为了不拷贝太多代码,我们直接用 collections.deque 就可以
快速实现一个简单的栈。
from collections import dequeclass Stack(object):def __init__(self):self._deque = deque()def push(self, value):return self._deque.append(value)def pop(self):return self._deque.pop()def is_empty(self):return len(self._deque) == 0def print_num_use_stack(n):s = Stack()while n > 0: # 不断将参数入栈s.push(n)n -= 1while not s.is_empty(): # 参数弹出print(s.pop())
这里结果也是输出 1 到 10,只不过我们是手动模拟了入栈和出栈的过程,帮助你理解计算机是如何实现递归的,是不是挺简单!现在你能明白为什么上边 print_num_recursive print_num_recursive_revserve 两个函数输出的区别了吗?
尾递归
上边的代码示例(麻雀虽小五脏俱全)中实际上包含了两种形式的递归,一种是普通的递归,还有一种叫做尾递归:
def print_num_recursive(n):if n > 0:print_num_recursive(n-1)print(n)def print_num_recursive_revserve(n):if n > 0:print(n)print_num_recursive_revserve(n-1) # 尾递归
概念上它很简单,就是递归调用放在了函数的最后。有什么用呢?
普通的递归, 每一级递归都产生了新的局部变量, 必须创建新的调用栈, 随着递归深度的增加, 创建的栈越来越多, 造成爆栈。虽然尾递归调用也会创建新的栈,
但是我们可以优化使得尾递归的每一级调用共用一个栈!, 如此便可解决爆栈和递归深度限制的问题!
不幸的是 python 默认不支持尾递归优化(见延伸阅读),不过一般尾递归我们可以用一个迭代来优化它。
汉诺塔问题
有三根杆子A,B,C。A杆上有N个(N>1)穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆:
但是有两个条件:
- 每次只能移动一个圆盘;
- 大盘不能叠在小盘上面。
最早发明这个问题的人是法国数学家爱德华·卢卡斯。
传说越南河内某间寺院有三根银棒,上串64个金盘。寺院里的僧侣依照一个古老的预言,以上述规则移动这些盘子;预言说当这些盘子移动完毕,世界就会灭亡。
这个传说叫做梵天寺之塔问题(Tower of Brahma puzzle)。但不知道是卢卡斯自创的这个传说,还是他受他人启发。

理解这个问题需要我们一些思维上的转换,因为我们正常的思维可能都是从上边最小的盘子开始移动,但是这里我们从移动最底下的盘子开始思考。
假设我们已经知道了如何移动上边的四个盘子到 B(pole2),现在把最大的盘子从 A -> C 就很简单了。当把最大的盘子移动到
C 之后,只需要把 B 上的 4 个盘子从 B -> C 就行。(这里的 pole1, 2, 3 分别就是 A, B, C 杆)

问题是仍要想办法如何移动上边的 4 个盘子,我们可以同样的方式来移动上边的 4 个盘子,这就是一种递归的解法。
给定 n 个盘子和三个杆分别是 源杆(Source), 目标杆(Destination),和中介杆(Intermediate),我们可以定义如下递归操作:
- 把上边的 n-1 个盘子从 S 移动到 I,借助 D 杆
- 把最底下的盘子从 S 移动到 D
- 把 n-1 个盘子从 I 移动到 D,借助 S
我们把它转换成代码:
def hanoi_move(n, source, dest, intermediate):if n >= 1: # 递归出口,只剩一个盘子hanoi_move(n-1, source, intermediate, dest)print("Move %s -> %s" % (source, dest))hanoi_move(n-1, intermediate, dest, source)
hanoi_move(3, 'A', 'C', 'B')# 输出,建议你手动模拟下。三个盘子 A(Source), B(intermediate), C(Destination)
"""
Move A -> C
Move A -> B
Move C -> B
Move A -> C
Move B -> A
Move B -> C
Move A -> C
"""
是不是很神奇,但是老实说这个过程仅凭大脑空想是比较难以想象出来的。人的大脑『栈』深度很有限,因为你甚至都没法同时记住超过 8 个以上的
无意义数字,所以用大脑模拟不如用纸笔来模拟下。(不排除有些聪明的同学能迅速在脑瓜里完成这个过程)
源码
# -*- coding: utf-8 -*-def fact(n):if n == 0:return 1else:return n * fact(n - 1)def print_num(n):for i in range(1, n + 1): # 注意很多编程语言使用的都是 从 0 开始的左闭右开区间, python 也不例外print(i)def print_num_recursive(n):if n > 0:print_num_recursive(n - 1)print(n)def print_num_recursive_revserve(n):if n > 0:print(n)print_num_recursive_revserve(n - 1)from collections import dequeclass Stack(object):def __init__(self):self._deque = deque()def push(self, value):return self._deque.append(value)def pop(self):return self._deque.pop()def is_empty(self):return len(self._deque) == 0def print_num_use_stack(n):s = Stack()while n > 0: # 不断将参数入栈s.push(n)n -= 1while not s.is_empty(): # 参数弹出print(s.pop())def hanoi_move(n, source, dest, intermediate):if n >= 1: # 递归出口,只剩一个盘子hanoi_move(n - 1, source, intermediate, dest)print("Move %s -> %s" % (source, dest))hanoi_move(n - 1, intermediate, dest, source)def flatten(rec_list):for i in rec_list:if isinstance(i, list):for i in flatten(i):yield ielse:yield idef test_flatten():assert list(flatten([[[1], 2, 3], [1, 2, 3]])) == [1, 2, 3, 1, 2, 3]
延伸阅读
递归是个非常重要的概念,我们后边的数据结构和算法中还会多次碰到它,我建议你多阅读一些资料加深理解:
- 《算法图解》第三章 递归
- 《Data Structures and Algorithms in Python》 第 10 章 Recursion
- 《Python开启尾递归优化!》
- 尾调用优化
- 汉诺塔
思考题
- 你能举出其他一些使用到递归的例子吗?
- 实现一个 flatten 函数,把嵌套的列表扁平化,你需要用递归函数来实现。比如 [[1,2], [1,2,3] -> [1,2,1,2,3]
- 使用递归和循环各有什么优缺点,你能想到吗?怎么把一个尾递归用迭代替换?
- 递归有时候虽然很优雅直观,但是时间复杂度却不理想,比如斐波那契数列,它的表达式是 F(n) = F(n-1) + F(n-2),你能计算它的时间复杂度吗?请你画个树来表示它的计算过程,为什么这个时间复杂度很不理想?我们怎样去优化它。
- python 内置的 dict 只能用 dict[‘key’] 的形式访问比较麻烦,我们想用 dict.key 的形式访问。tornado web 框架中提供了一个 ObjectDict,请你实现一个递归函数接收一个字典,并返回一个可以嵌套访问的 ObjectDict
相关文章:

python数据结构与算法-10_递归
递归 Recursion is a process for solving problems by subdividing a larger problem into smaller cases of the problem itself and then solving the smaller, more trivial parts. 递归是计算机科学里出现非常多的一个概念,有时候用递归解决问题看起来非常简单…...

如何设计鞋材出库入账管理系统
如何设计鞋材出库入账管理系统 系统概述系统需求分析系统设计系统实施与测试系统上线与维护 系统概述 本系统旨在设计一个针对鞋材出库入账管理的数字化解决方案,以提高管理效率、降低运营成本并确保材料账目清晰。系统将结合先进的信息化技术,实现对鞋…...

一个简单的QT应用示例
一个简单的QT应用示例:创建一个窗口程序。 首先,确保已经安装了Qt开发环境。接下来,按照以下步骤创建一个简单的窗口程序: 1. 打开Qt Creator,点击“新建文件或项目”。 2. 选择“应用程序”,然后点击“下…...
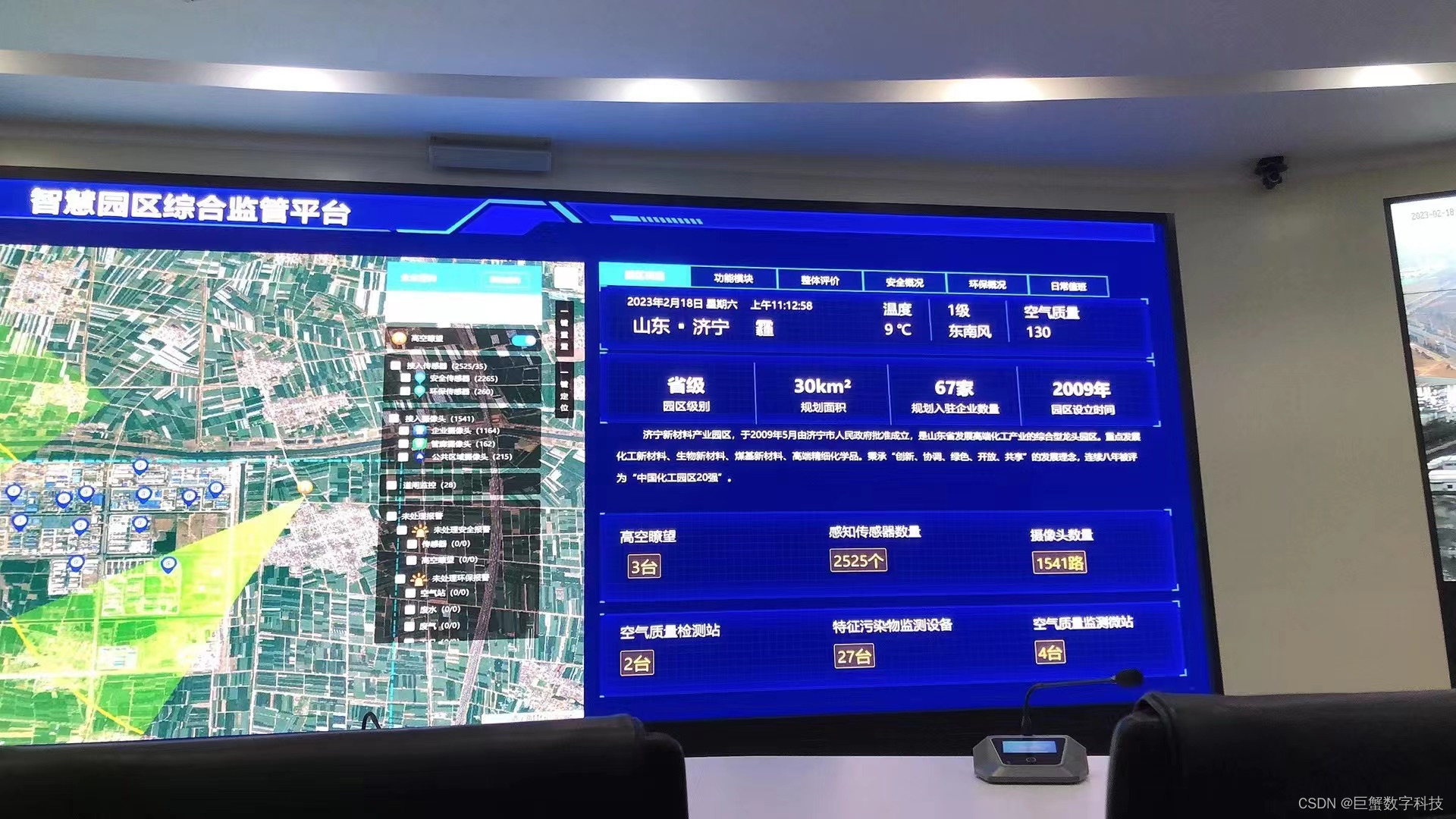
南京数字孪生赋能工业制造,加速推进制造业数字化转型
随着南京信息技术的迅猛发展和工业管理的不断演进,传统的工业管理方式已经无法满足企业对高效、智能和可持续发展的需求。针对这一情况,数字孪生技术应运而生,为南京工业管理带来了全新的变革和机遇。以数字孪生为理念,三维可视化…...
Visual Studio Code 从英文界面切换中文
1、先安装中文的插件,直接安装。 2、点击右下角的 change language restart, 让软件重启即可以完成了。...

邦芒支招:利用自荐电话求职的七大技巧
如何利用自荐电话向招聘官推荐自己,现在人们在求职过程中都会自己争取面试机会,其中自荐电话是比较常见的一种方式,但是想要向面试官成功推荐自己也是不容易的,下面分享如何利用自荐电话向招聘官推荐自己。 1、以对方为…...

埃尔米特插值(hermite 插值) C++
埃尔米特插值 原理 #pragma once #include <vector> #include <functional> /*埃尔米特插值*/ struct InterpolationPoint {double x; // 插值点的横坐标double y; // 插值点的纵坐标double derivative; // 插值点的导数值// 默认构造函数InterpolationPoint() : x…...

mysql优化之explain 以及 索引优化
Mysql安装文档参考:https://blog.csdn.net/yougoule/article/details/56680952 Explain工具介绍 使用EXPLAIN关键字可以模拟优化器执行SQL语句,分析你的查询语句或是结构的性能瓶颈 在 select 语句之前增加 explain 关键字,MySQL 会在查询上设…...
)
WebSocket --- ws模块源码解析(详解)
摘要 在这一篇文章中,写了如何在node端和web端,实现一个WebSocket通信。 WebSocket在node端和客户端的使用 而在node端里面,我们使用了ws模块来创建WebSocket和WebSocketServer,那ws模块是如何做到可以和客户端进行双向通信的呢…...

一文带你拿下MySQL之增删查改(基础)
✏️✏️✏️今天给各位带来的是关于数据库增删查改基础方面的知识。 清风的CSDN博客 😛😛😛希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,大家一起学习交流! 动动你们发财的小手…...

2023亿发数字化智能工单,专业管理工单处理全流程,助力企业转型腾飞
伴随着智能化和信息化的不断深入,企业数字化转型势如腾飞。在这个过程中,工单管理成为生产、家电、后勤等多个管理场景下频繁应用的关键环节。如何满足管理方对设备、服务等智能化管理的需求,提升工单管理效率、规范管理流程,并实…...

JavaScript 常用符号
JavaScript是一门基础性的编程语言,常用于web开发中。JS中有许多特殊的符号,这些符号的用法十分重要,直接影响代码的正确性和可读性。在日常编写中,我们会频繁使用以下几个符号。 一、等于号() 等于号在JS…...

GPT-4:论文阅读笔记
GPT-4的输入和输出:输入的内容是文本或图片,输出的内容是文本。因此,GPT-4是一种输入端多模态的模型。GPT-4的效果:在真实世界中还是比不上人类,但是在很多专业性的任务上已经达到了人类的水平,甚至超过人类…...

hm商城微服务远程调用及拆分
RequiredArgsConstructor是Lombok库中的一个注解 它会自动在类中生成一个构造函数,这个构造函数会接收类中所有被标记为final的字段,并将其作为参数。这个注解可以帮助我们减少样板代码,例如手动编写构造函数。 eg: public fin…...
设置指定时间之前的时间不可选
1、el-date-picker设置今天之前的日期不可选 <el-date-picker style"width: 100%" type"date" v-model"form.resetDate" align"right" :value-format"yyyy-MM-dd" placeholder"选择调整日期":disabled"t…...

Java使用Redis来实现分布式锁
Java使用Redis来实现分布式锁 在单节点服务中,我们可以使用synchronized来保证同一时间内只允许一个线程执行限定的代码块。但是如果我们是多节点服务呢,因为synchronized是针对服务内部的,其他服务是无法受到他的干预的。那么如何保证多个节…...
移动端表格分页uni-app
使用uni-app提供的uni-table表格 网址:https://uniapp.dcloud.net.cn/component/uniui/uni-table.html#%E4%BB%8B%E7%BB%8D <uni-table ref"table" :loading"loading" border stripe type"selection" emptyText"暂无更多数据…...

全志R128芯片RTOS调试指南
RTOS 调试指南 此文档介绍 FreeRTOS 系统方案支持的常用软件调试方法,帮助相关开发人员快速高效地进行软件调试,提高解决软件问题的效率。 栈回溯 栈回溯是指获取程序的调用链信息,通过栈回溯信息,能帮助开发者快速理清程序执行…...

超级实用的程序员接单平台,看完少走几年弯路,强推第一个!
“前途光明我看不见,道路曲折我走不完。” 兜兜转转,心心念念,念念不忘,必有回响。终于找到了… 网络上好多人都在推荐程序员线上接单,有人说赚得盆满钵满,有的人被坑得破口大骂,还有的人甚至还…...

前端字符串方法汇总
1、length属性 const sss lengthconsole.log(字符串长度是, sss.length) 2、chartAt() charAt()和charCodeAt()方法都可以通过索引来获取指定位置的值: charAt() 方法获取到的是指定位置的字符;charCodeAt()方法获取的是指定位置字符的Unicode值。 …...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
