2.递归算法
递归算法的两个特点(很重要)
调用自身
要有结束条件
void func1(int x)
{printf("%d\n", x);func1(x - 1);
}func1会一直死循环,没有使其结束的条件,所以不是递归
void func2(int x)
{if (x > 0){printf("%d\n", x);func2(x + 1);}
}func2当传入的x > 0时,会一直死循环,此时没有使其结束的条件,所以不是递归
void func3(int x)
{if (x > 0){printf("%d\n", x);func3(x - 1);}
}func3是递归,满足递归的两个特点,调用自身,有结束条件

输出结果为:3 2 1
void func4(int x)
{if (x > 0){func4(x - 1);printf("%d\n", x);}
}func4是递归,满足递归的两个特点,调用自身,有结束条件

输出结果为:1 2 3
递归实例:汉诺塔问题
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。

分析:
当A柱子只有1个盘子时
A移动到B
当A柱子有2个盘子时
A移动到C
A移动到B
C移动到A
当A柱子有n个盘子时,将A柱子中的第n个盘子看作一个整体,A柱子中的1, 2, ..., n-1看作一个整体
hanoi(n - 1)从A移动到C
A移动到B
hanoi(n - 1)从C移动到B
源码:
#include <stdio.h>long long g_counter = 0;
void move(int n, char a, char b)
{g_counter++;printf("第%d次移动,将第%d个盘子从%c移动到%c\n", g_counter, n, a, b);
}
void hanoi(int n, char a, char b, char c)
{ if (n == 1){move(n, a, b);}else{hanoi(n-1, a, b, c);move(n, a, b);hanoi(n-1, c, a, b);}
}int main(int argc, char *argv[])
{int n = 3;printf("请输入汉诺塔的层数:\n");scanf("%d", &n);hanoi(n, 'A', 'B', 'C');return 0;
}结果
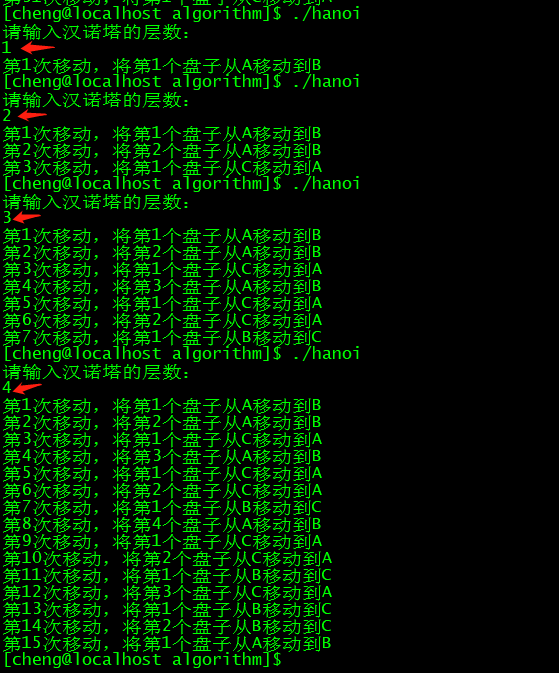
ending😃
相关文章:

2.递归算法
递归算法的两个特点(很重要)调用自身要有结束条件void func1(int x) {printf("%d\n", x);func1(x - 1); }func1会一直死循环,没有使其结束的条件,所以不是递归void func2(int x) {if (x > 0){printf("%d\n"…...

MySQL---触发器
MySQL—触发器 将两个关联的操作步骤写到程序里面,并且要用事务包裹起来,确保两个操作称为一个原子操作,要么全部执行,要么全部不执行 创建一个触发器,让商品信息数据的插入操作自动触发库存数据的插入操作 …...
PXC高可用集群(MySQL)
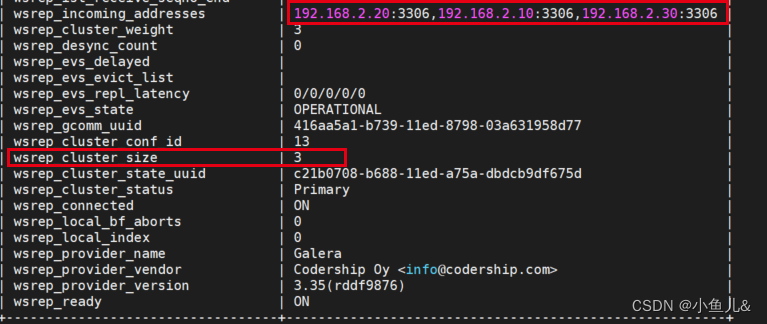
1. PXC集群概述 1.1. PXC介绍 Percona XtraDB Cluster(简称PXC) 是基于Galera的MySQL高可用集群解决方案Galera Cluster是Codership公司开发的一套免费开源的高可用方案PXC集群主要由两部分组成:Percona Server with XtraDB(数据…...
pytorch-把线性回归实现一下。原理到实现,python到pytorch
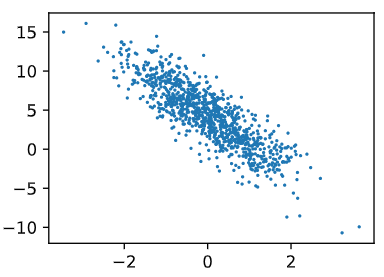
线性回归 线性回归输出是一个连续值,因此适用于回归问题。回归问题在实际中很常见,如预测房屋价格、气温、销售额等连续值的问题。 与回归问题不同,分类问题中模型的最终输出是一个离散值。所说的图像分类、垃圾邮件识别、疾病检测等输出为离…...

js中判断数组的方式有哪些?
js中判断数组的方式有哪些?1.通过Object.prototype.toString.call来判断2.通过instanceof来判断3.通过constructor来判断4.通过原型链来判断5.通过ES6.Array.isAaary()来判断6.通过Array.prototype.isPrototypeOf来判断1.通过Object.prototype.toString.call来判断 …...

【2023unity游戏制作-mango的冒险】-5.攻击系统的简单实现
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:unity游戏制作 ⭐攻击系统的简单实现⭐ 文章目录⭐攻击系统的简单实现⭐👨…...

SpringMVC 面试题
1、什么是SpringMVC? SpringMVC是一个基于Java的实现了MVC设计模式的“请求驱动型”的轻量级WEB框架,通过把model,view,controller 分离,将web层进行职责的解耦,把复杂的web应用分成逻辑清晰的几个部分&am…...

布局三八女王节,巧借小红书数据分析工具成功引爆618
对于小红书“她”经济来说,没有比三八节更好的阵地了。伴随三八女王节逐渐临近,各大品牌蓄势待发,这场开春后第一个S级大促活动,看看品牌方们可以做什么? 洞察流量,把握节点营销时机 搜索小红书2023年的三…...
RISCV学习(1)基本模型认识
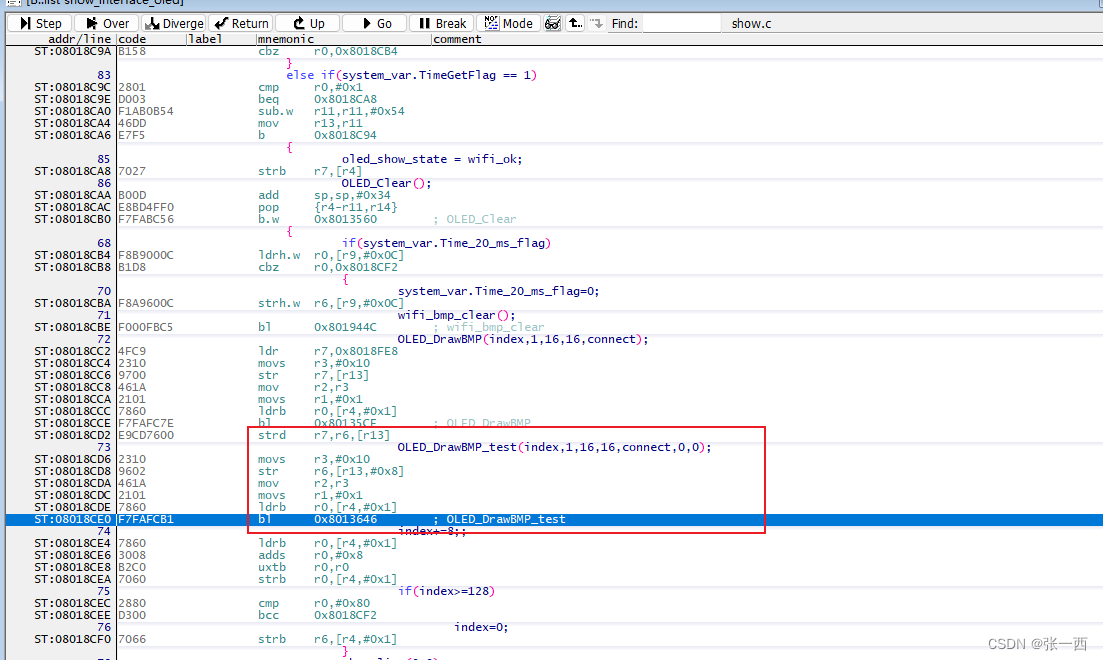
笔者来聊聊ARM的函数的调用规则 1、ARM函数调用规则介绍 首先介绍几个术语, AAPCS:Procedure Call Standard for the ARM ArchitectureAPCS:ARM Procedure Call StandardTPCS:Thumb Procedure Call StandardATPCS:AR…...

【java代码审计】命令注入
1 成因 开发者在某种开发需求时,需要引入对系统本地命令的支持来完成某些特定的功能,此时若未对用户的输入做严格的过滤,就可能发生命令注入。 2 造成命令注入的类或方法 Runtime类:提供调用系统命令的功能 ①Runtime.getRuntim…...
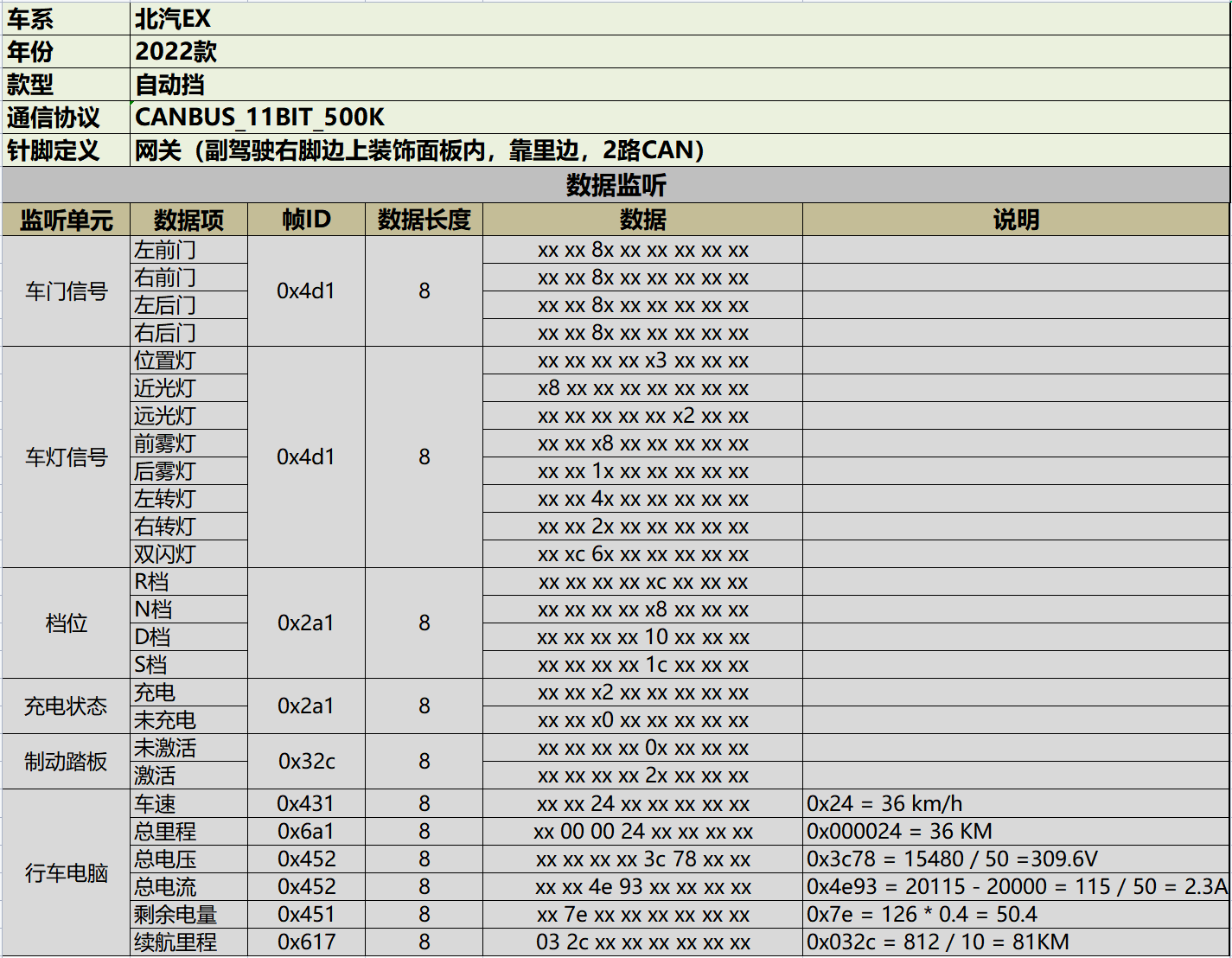
速锐得适配北汽EX系列电动汽车CAN总线应用于公务分时租赁
过去的几年,我们看到整个分时租赁业务出现断崖式下跌,这是我们看到这种市场情况,是必然,也是出乎意料。原本很多融资后的出行公司、大牌的出行服务商的分时租赁业务,受各种影响不得不转型成其他出行服务。例如…...

已解决ERROR: Failed building wheel for opencv-python-headless
已解决ERROR: Failed building wheel for opencv-python-headless Failed to build opencv-python-headless ERROR: Could not build wheels for opencv-python-headless, which is required to install pyproject.toml-based projects报错信息亲测有效 文章目录报错问题报错翻…...

每日获取安全资讯的网站,国内外共120个
国内 FreeBuf(https://www.freebuf.com/) 安全客(https://www.anquanke.com/) 雷锋网安全(https://www.leiphone.com/category/security) 先知社区(https://xz.aliyun.com/) CSDN安全…...

HUN工训中心:开关电路和按键信号抖动
工训中心的牛马实验 1.实验目的: 1) 认识开关电路,掌握按键状态判别、开关电路中逻辑电平测量、逻辑值和逻辑函数电路。 2) 掌握按键信号抖动简单处理方法。 3) 实现按键计数电路。 2.实验资源: HBE硬件基础电路实验箱、示波器、万用表…...
)
WordPress 主题 SEO 标题相关函数和过滤器教程wp_get_document_title()
WordPress 4.4.0 版本开始,加入了 wp_get_document_title(); 这个函数,而 wp_title(); 已经 deprecated 不推荐使用。因此,如果想要启用 WordPress 主题标题功能,在不安装 WordPress SEO 插件的情况下,可以使用以下代码…...
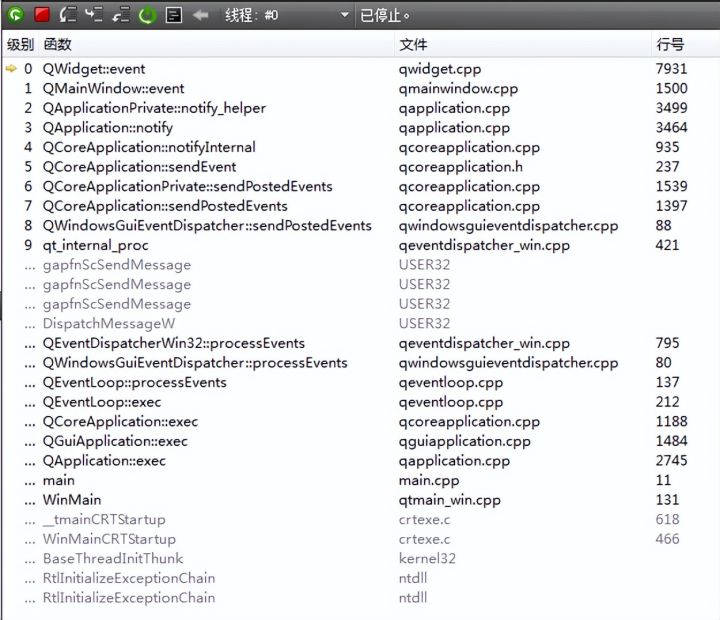
Qt 事件机制
【1】事件 事件是可以被控件识别的操作。如按下确定按钮、选择某个单选按钮或复选框。 每种控件有自己可识别的事件,如窗体的加载、单击、双击等事件,编辑框(文本框)的文本改变事件等等。 事件就是用户对窗口上各种组件的操作。…...
求对称矩阵的特征值和特征向量)
【Python】Numpy--np.linalg.eig()求对称矩阵的特征值和特征向量
【Python】Numpy–np.linalg.eig()求对称矩阵的特征值和特征向量 文章目录【Python】Numpy--np.linalg.eig()求对称矩阵的特征值和特征向量1. 介绍2. API3. 代码示例1. 介绍 特征分解(Eigendecomposition),又称谱分解(Spectral d…...
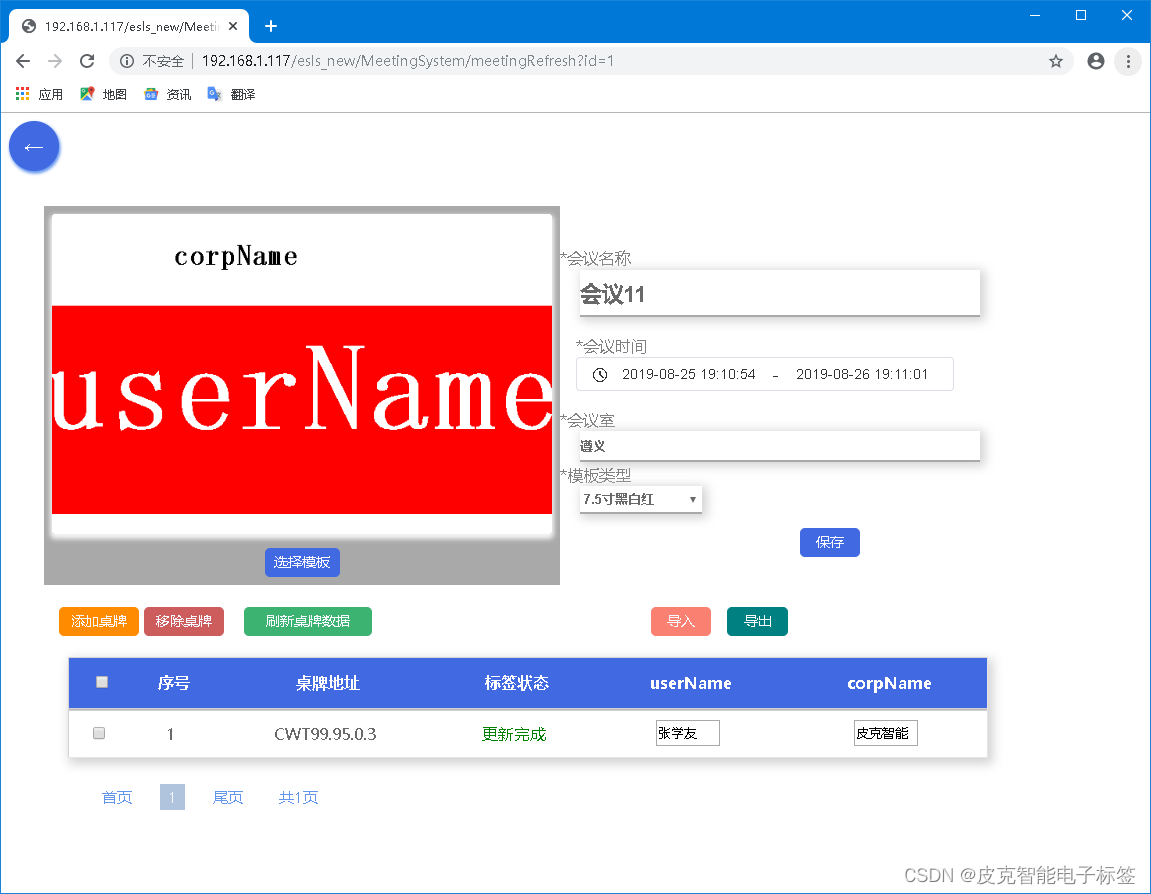
医疗床头卡(WIFI方案)
一、产品特性 7.5寸墨水屏显示WIFI无线通信,极简部署,远程控制按键及高亮LED指示灯指示800*480点阵屏幕锂电池供电,支持USB充电DIY界面支持文本/条码/二维码/图片超低功耗/超长寿命,一次充电可用一年基于现有Wifi环境,…...
[YOLO] yolo博客笔记汇总(自用
pip下载速度太慢,国内镜像: 国内镜像解决pip下载太慢https://blog.csdn.net/weixin_51995286/article/details/113972534 YOLO v2和V3 关于设置生成anchorbox,Boundingbox边框回归的过程详细解读 YOLO v2和V3 关于设置生成an…...
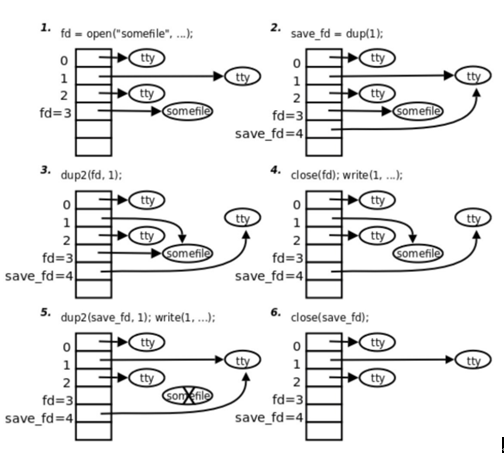
Linux 常用 API 函数
文章目录1. 系统调用与库函数1.1 什么是系统调用1.2 系统调用的实现1.3 系统调用和库函数的区别2. 虚拟内存空间3. 错误处理函数4. C 库中 IO 函数工作流程5. 文件描述符6. 常用文件 IO 函数6.1 open 函数6.2 close 函数6.3 write 函数6.4 read 函数6.5 lseek 函数7. 文件操作相…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...
