华为ospf路由协议防环和次优路径中一些难点问题分析
第一种情况是ar3的/0/0/2口和ar4的0/0/2口发布在区域1时,当ar1连接ar2的线断了以后,骨干区域就断了,1.1.1.1到2.2.2.2就断了,ping不通了。但ar5和ar6可以ping通2.2.2.2和1.1.1.1,ar3和ar4不可以ping通2.2.2.2和1.1.1.1,虽然ar3和ar4中的lsdb中有ar1和ar2的lsdb,但就是不计算路由不通,原因是ar3从ar4学到的2.2.2.2,ar4从ar3学到了1.1.1.1,但是ospf原理是abr不计算非骨干区域学到的三类lsa所以不通
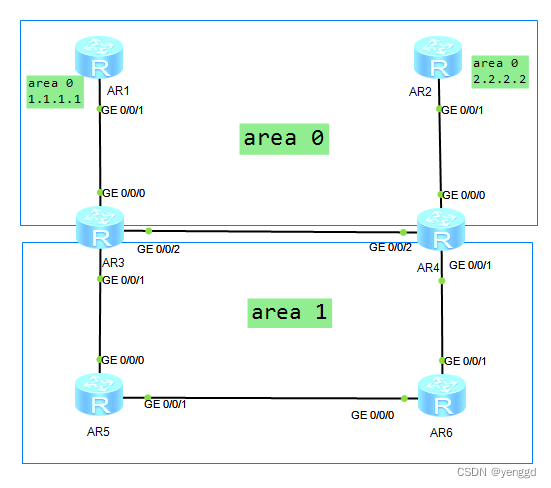
第二种情况(产生次优路径):
ar3的g0/0/2口和ar4的g0/0/02发布在区域0时,且ar3的3.3.3.3和ar4的4.4.4.4发布在区域1时,3.3.3.3访问4.4.4.4时,走下面ar5->ar6绕行,原因就是区域内的路由优于区间路由,所以产生了次优路径。

第三种情况(虚链路解决次优路径):
ar3的g0/0/2口和ar4的g0/0/02发布在区域1时,且ar3的3.3.3.3和ar4的4.4.4.4发布在区域1时,不但ar3和ar4用区域1,并建立了vlink-peer,逻辑上变成了区域0,解决了次优路径,3.3.3.3访问4.4.4.4时,ar3-ar4直接通行。
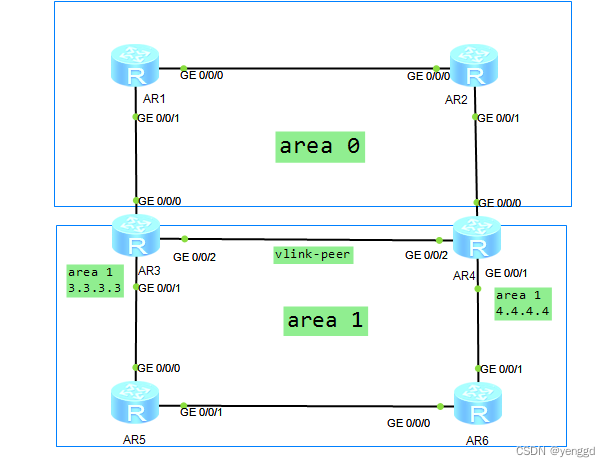
第四种情况(子接口解决次优路径和并实现备注骨干区域):
ar3的g0/0/2口和ar4的g0/0/2发布在区域0时,再把ar3的g0/0/2.2子接口和ar4的g0/0/02.2子接口发布在区域1,这样不但解决了骨干区域的备份问题,当AR1到AR2的链路断裂后,全网照样畅通,还解决了次优路径,3.3.3.3访问4.4.4.4时,ar3-ar4直接通行。
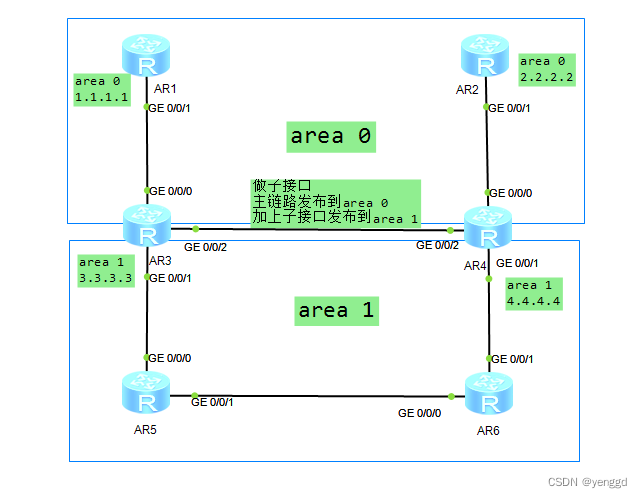
相关文章:

华为ospf路由协议防环和次优路径中一些难点问题分析
第一种情况是ar3的/0/0/2口和ar4的0/0/2口发布在区域1时,当ar1连接ar2的线断了以后,骨干区域就断了,1.1.1.1到2.2.2.2就断了,ping不通了。但ar5和ar6可以ping通2.2.2.2和1.1.1.1,ar3和ar4不可以ping通2.2.2.2和1.1.1.1…...
python-opencv划痕检测-续
python-opencv划痕检测-续 这次划痕检测,是上一次划痕检测的续集。 处理的图像如下: 这次划痕检测,我们经过如下几步: 第一步:读取灰度图像 第二步:进行均值滤波 第三步:进行图像差分 第四步࿱…...

c++[string实现、反思]
我的码云 我的string码云 分析总结 1.项目结构 所有的类和函数需要在namespace中实现,要和string高度对应 private:char* _str;//字符串size_t _size;//有效长度size_t _capacity;//总空间,包括\0const static size_t npos-1;2.定义变量 <1> 所…...

c++版本opencv计算灰度图像的轮廓点
代码 #include<iostream> #include<opencv.hpp>int main() {std::string imgPath("D:\\prostate_run\\result_US_20230804_141531\\mask\\us\\104.bmp");cv::Mat imgGray cv::imread(imgPath, 0);cv::Mat kernel cv::getStructuringElement(cv::MORPH…...

【05】ES6:函数的扩展
一、函数参数的默认值 ES6 允许为函数的参数设置默认值,即直接写在参数定义的后面。 1、基本用法 默认值的生效条件 不传参数,或者明确的传递 undefined 作为参数,只有这两种情况下,默认值才会生效。 注意:null 就…...
Ubuntu20.04安装搜狗输入法
1、安装包下载 搜狗输入法linux-首页搜狗输入法for linux—支持全拼、简拼、模糊音、云输入、皮肤、中英混输https://shurufa.sogou.com/linux点击立即下载,根据自己的硬件选择deb安装包。 2、输入法安装 当第一步完成以后,页面会自动跳转至搜狗的安装…...

linux的基础命令
文章目录 linux的基础命令一、linux的目录结构(一)Linux路径的描述方式 二、Linux命令入门(一)Linux命令基础格式 三、ls命令(一)HOME目录和工作目录(二)ls命令的参数1.ls命令的-a选…...

linux查询某个进程使用的内存量
linux查询某个进程使用的内存量 查进程用的内存,查看进程占用的内存量,centos查询内存使用 查某个进程id使用的内存量 ps -p 24450 -o rss | awk {print int($1/1024)"MB"} 该命令的含义是: ps -p 24450: 查找进程ID为24450的进…...

list的总结
目录 1.什么是list 1.1list 的优势和劣势 优势: 劣势: 2.构造函数 2.1 default (1) 2.2 fill (2) 2.3 range (3) 2.4 copy (4) 3.list iterator的使用 3.1. begin() 3.2. end() 3.3迭代器遍历 4. list容量函数 4.1. empty() 4.2. siz…...
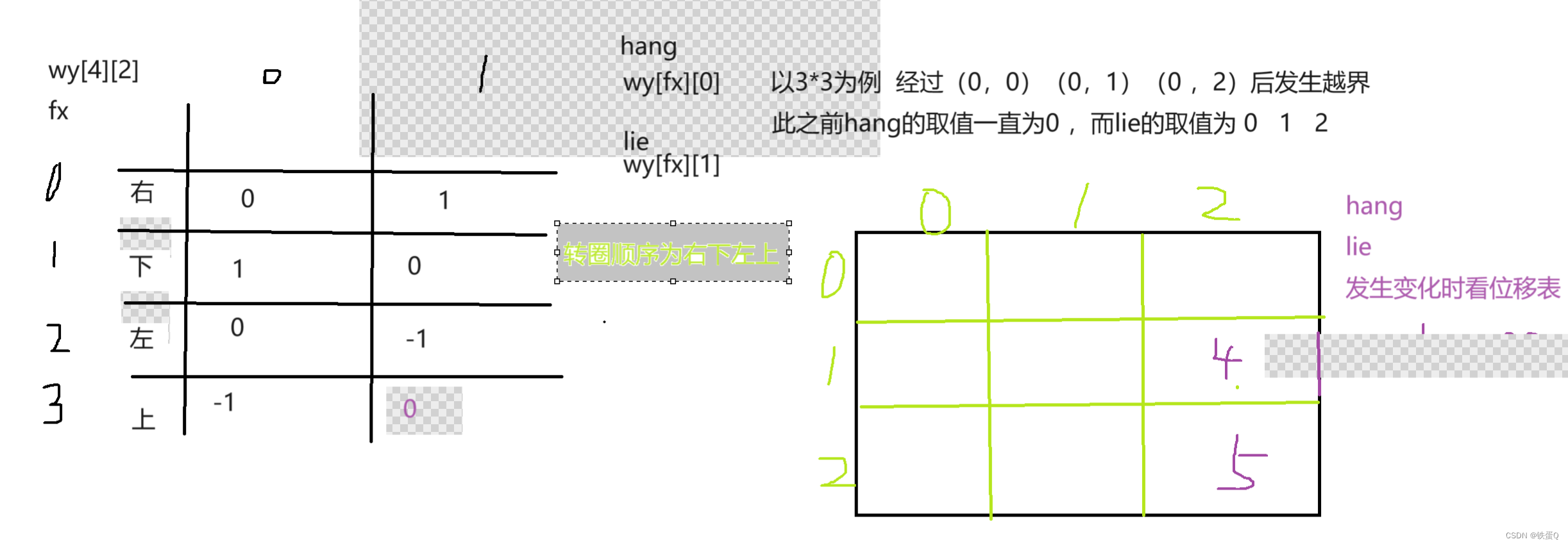
c语言数字转圈
数字转圈 题干输入整数 N(1≤N≤9),输出如下 N 阶方阵。 若输入5显示如下方阵: * 1** 2** 3** 4** 5* *16**17**18**19** 6* *15**24**25**20** 7* *14**23**22**21** 8* *13**12**11**10** 9*输入样例3输出样例* 1*…...
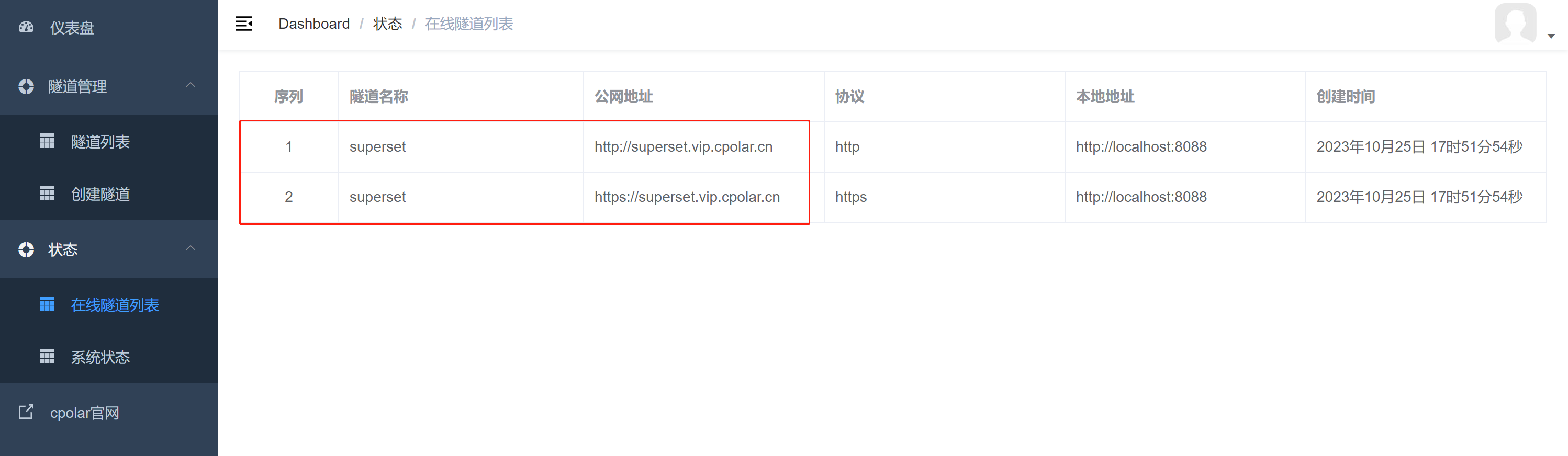
Apache Superset数据分析平台如何实现公网实时远程访问数据【内网穿透】
文章目录 前言1. 使用Docker部署Apache Superset1.1 第一步安装docker 、docker compose1.2 克隆superset代码到本地并使用docker compose启动 2. 安装cpolar内网穿透,实现公网访问3. 设置固定连接公网地址 前言 Superset是一款由中国知名科技公司开源的“现代化的…...
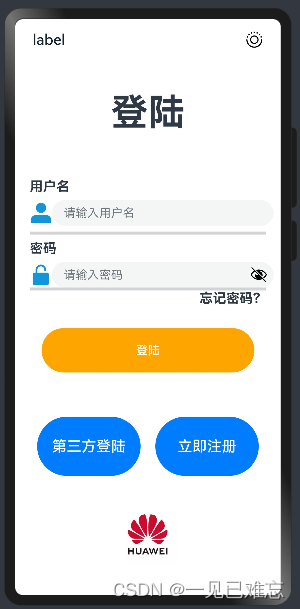
HarmonyOS应用开发实战—登录页面【ArkTS】
文章目录 本页面实战效果预览图一.HarmonyOS应用开发1.1HarmonyOS 详解1.2 ArkTS详解二.HarmonyOS应用开发实战—登录页面【ArkTS】2.1 ArkTS页面源码2.2 代码解析2.3 心得本页面实战效果预览图 一.HarmonyOS应用开发 1.1HarmonyOS 详解 HarmonyOS(鸿蒙操作系统)是华为公司…...

@RequestMapping
目录 作用: 位置: 属性 1.value 2.method 3.params 4.header 作用: 该注解是一个用来处理请求地址映射的注解。 位置: 可用于映射一个请求或一个方法,可以用在类或方法上。 用于方法上,表示在类的…...

操作系统 应用题 例题+参考答案(考研真题)
1.(考研真题)一个多道批处理系统中仅有P1和P2两个作业,P2比P1晚5ms到达,它们的计算和I/O操作顺序如下。 P1:计算60ms,I/O 80ms,计算20ms。 P2:计算120ms,I/O 40ms&…...
免费获取GPT-4的五种工具
不可否认,由OpenAI带来的GPT-4已是全球最受欢迎的、功能最强大的大语言模型(LLM)之一。大多数人都需要使用ChatGPT Plus的订阅服务去访问GPT-4。为此,他们通常需要每月支付20美元。那么问题来了,如果您不想每月有这笔支…...

XTU OJ 1146 矩阵乘法学习笔记
原题 题目描述 给你两个矩阵A(n*k),B(k*m),请求A*B。 输入 第一行是一个整数K,表示样例的个数。 每个样例包含两个矩阵A和B。 每个矩阵的第一行是两个整数n,m,(1≤n,m≤10)表示矩阵的行和列 以后的n行,每行m个整数,每个整数的绝对值不超过…...
基于官方YOLOv4开发构建目标检测模型超详细实战教程【以自建缺陷检测数据集为例】
本文是关于基于YOLOv4开发构建目标检测模型的超详细实战教程,超详细实战教程相关的博文在前文有相应的系列,感兴趣的话可以自行移步阅读即可:《基于yolov7开发实践实例分割模型超详细教程》 《YOLOv7基于自己的数据集从零构建模型完整训练、…...

1、Docker概述与安装
相关资源网站: ● docker官网:http://www.docker.com ● Docker Hub仓库官网: https://hub.docker.com/ 注意,如果只是想看Docker的安装,可以直接往下拉跳转到Docker架构与安装章节下的Docker具体安装步骤,一步步带你安…...

论文笔记——FasterNet
为了设计快速神经网络,许多工作都集中在减少浮点运算(FLOPs)的数量上。然而,作者观察到FLOPs的这种减少不一定会带来延迟的类似程度的减少。这主要源于每秒低浮点运算(FLOPS)效率低下。 为了实现更快的网络,作者重新回顾了FLOPs的运算符,并证明了如此低的FLOPS主要是由…...

计算机组成原理-固态硬盘SSD
文章目录 总览机械硬盘vs固态硬盘固态硬盘的结构固态硬盘与机械硬盘相比的特点磨损均衡技术例题 总览 机械硬盘vs固态硬盘 固态硬盘采用闪存技术,是电可擦除ROM 下图右边黑色的块块就是一块一块的闪存芯片 固态硬盘的结构 块大小16KB~512KB 页大小512B~4KB 对固…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
