git本地账户如何从一台电脑迁移到另外一台
为了表述方便,我们此处用旧电脑、新电脑指代。
在新电脑上安装git
例如,我旧电脑上安装的git版本是2.33.1版本,新电脑安装git的版本是2.43.0,这不妨碍迁移。
将git的全局配置文件从旧电脑拷贝到新电脑
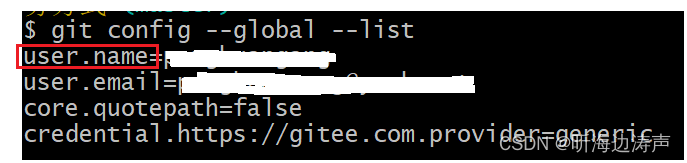
Git的全局配置文件,名字是.gitconfig,是使用git config --global --list命令可以查看到的内容。这个文件在旧电脑的文件路径是C:\Users\<旧电脑中的用户名>\.gitconfig,例如C:\Users\Administrator\.gitconfig。
将这个文件从旧电脑上拷贝新电脑的C:\Users\<新电脑中的用户名>的目录下。假设新电脑的用户名是YL,拷贝完成后,文件路径是C:\Users\YL\.gitconfig。
拷贝过来后,在新电脑上,运行git config --global --list命令查看,能够看到正确的内容了。
将公钥和私钥文件从旧电脑拷贝到新电脑
将旧电脑的C:\Users\<旧电脑中的用户名>\.ssh目录 拷贝到 新电脑的C:\Users\<新电脑中的用户名>目录下。
往远端仓库推送还需要知道用户名和AcessToken
上面的步骤做完后,在本地git仓库中add、commit什么的都是可以的了。
但往远端仓库(例如gitee)push的时候,提醒要输入用户名和密码:
此处的用户名就是填写以前push到远端仓库使用的用户名(通过 git config --global --list命令也能查看用户名),密码填写以前在远端仓库(例如gitee)生成的AcessToken(备注:AcessToken是以前登录远端仓库生成的,当时应该记录下来的,因为后面再登录就看不到了)。
然后就能正常往远端仓库推送了。
相关文章:

git本地账户如何从一台电脑迁移到另外一台
为了表述方便,我们此处用旧电脑、新电脑指代。 在新电脑上安装git 例如,我旧电脑上安装的git版本是2.33.1版本,新电脑安装git的版本是2.43.0,这不妨碍迁移。 将git的全局配置文件从旧电脑拷贝到新电脑 Git的全局配置文件&…...
HOOPS Web平台助力开发3D应用,实现超大规模3D web轻量化渲染与数据格式转换!
一、包含的软件开发工具包 HOOPS Web平台帮助开发人员构建基于Web的工程应用程序,提供高级3D Web可视化、准确快速的CAD数据访问和3D数据发布。 HOOPS Web平台包括三个集成软件开发工具包 (SDK): (1)Web端3D可视化引擎 HOOPSCom…...

GDB Debugging Notes
1 Debugging programs using gdb 1.1 gdb简介 gdb是一个功能强大的调试工具,可以用来调试C程序或C程序。在使用这个工具进行程序调试时,主要涉及下面几个方面的操作: 启动程序:在启动程序时,可以设置程序运行环境。设置断点:程序…...
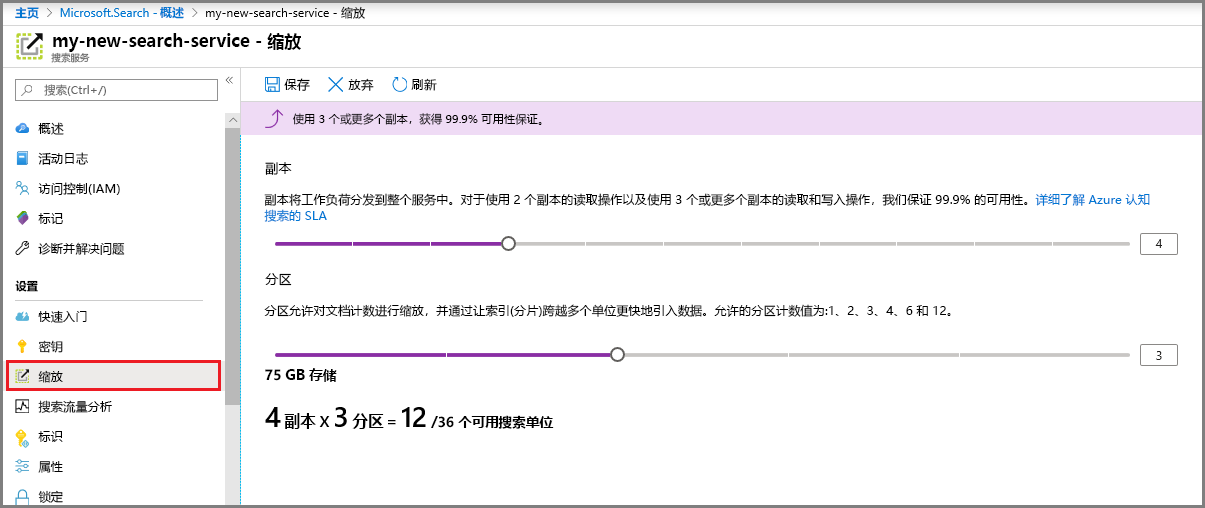
Azure Machine Learning - 创建Azure AI搜索服务
目录 准备工作查找 Azure AI 搜索产品/服务选择订阅设置资源组为服务命名选择区域选择层创建服务配置身份验证扩展服务何时添加第二个服务将多个服务添加到订阅 Azure AI 搜索是用于将全文搜索体验添加到自定义应用的 Azure 资源,本文介绍如何创建Azure AI搜索服务 …...
鸿蒙(HarmonyOS)应用开发——安装DevEco Studio安装
前言 HarmonyOS华为开发的操作系统,旨在为多种设备提供统一的体验。它采用了分布式架构,可以在多个设备上同时运行,提供更加流畅的连接和互动。HarmonyOS的目标是提供更高的安全性、更高效、响应更快的用户体验,并通过跨设备功能…...
成都数字孪生技术推进制造业升级,工业物联网可视化应用加速
成都数字孪生技术推进制造业升级,工业物联网可视化应用加速。灯塔工厂转型的关键在于第四次工业革命新技术的应用。数字孪生灯塔工厂是工业4.0技术的应用典范,工业4.0的核心技术包括:数字孪生、大数据分析,工业物联网,…...

管理类联考——数学——汇总篇——知识点突破——代数——函数——记忆
文章目录 整体文字提炼图像绘画 考点记忆/考点汇总——按大纲 本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多&am…...
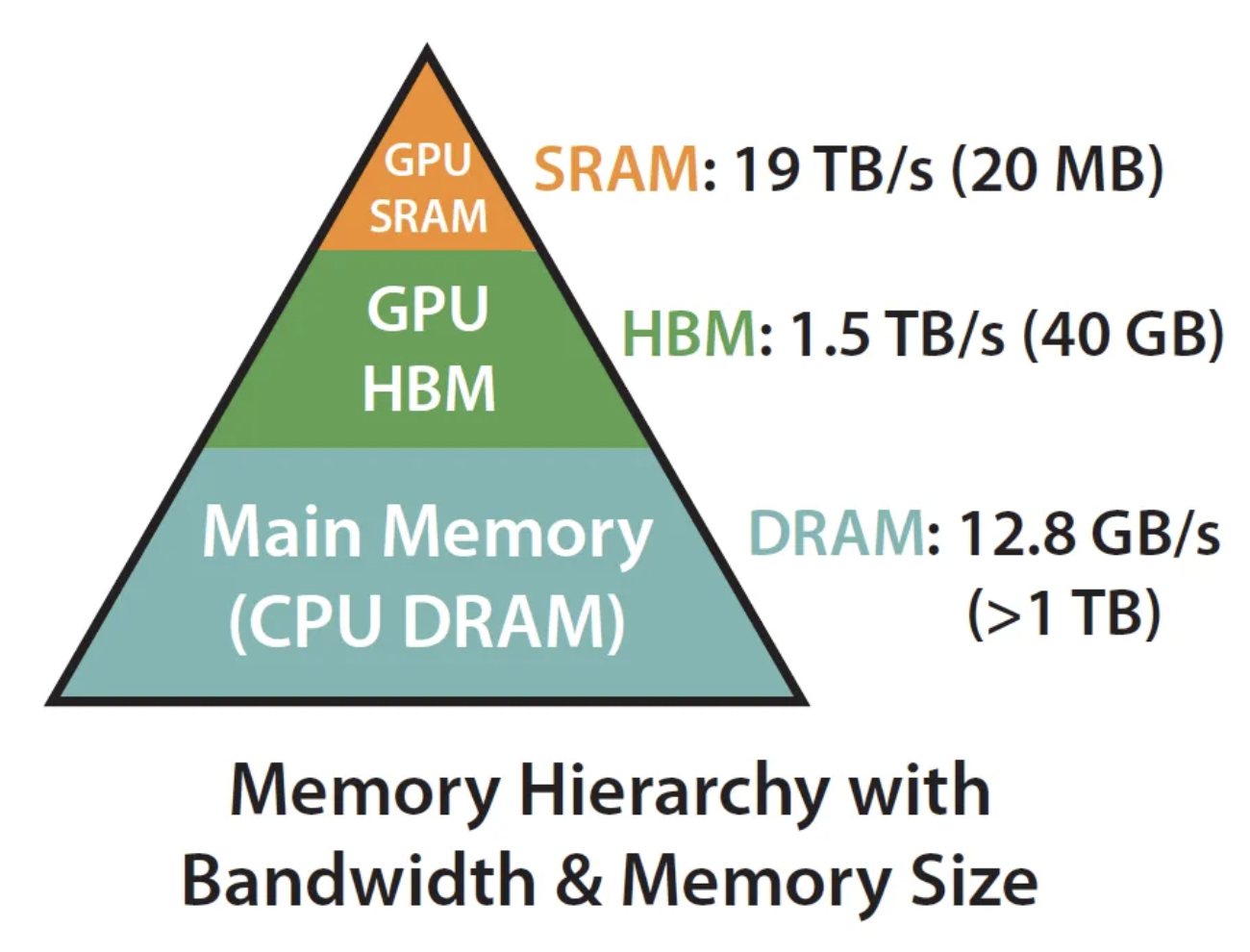
Flash Attention:高效注意力机制的突破与应用
注意力机制彻底改变了自然语言处理和深度学习领域。它们允许模型在执行机器翻译、语言生成等任务时专注于输入数据的相关部分。 在这篇博客[1]中,我们将深入研究被称为“Flash Attention”的注意力机制的突破性进展。我们将探讨它是什么、它是如何工作的,…...

Flutter开发警告Constructors in ‘@immutable‘ classes should be declared as ‘const‘
文章目录 警告信息报错代码警告原因修改后的代码 警告信息 Flutter开发遇到如下警告 Constructors in ‘immutable’ classes should be declared as ‘const’. 报错代码 class TaskWidget extends StatefulWidget {final String title;final bool isChecked;final int ord…...

想当老师应该去学什么专业
专业选择是决定未来职业发展的重要步骤,如果你也想成为一名老师,那么这五个专业可能会适合你! 教育学专业 教育学专业是培养教育理论和方法的学科,这些理论知识将帮助你理解教学过程、学生发展、课程设计和评估。该专业将让你全面…...
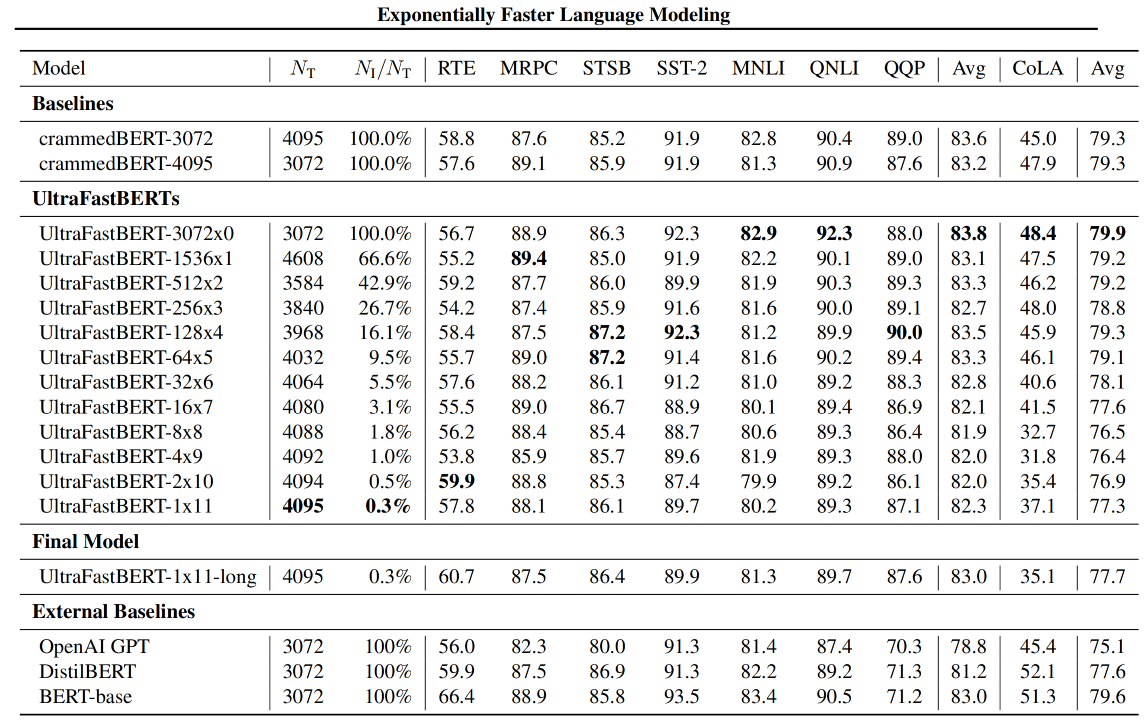
【LM、LLM】浅尝二叉树在前馈神经网络上的应用
前言 随着大模型的发展,模型参数量暴涨,以Transformer的为组成成分的隐藏神经元数量增长的越来越多。因此,降低前馈层的推理成本逐渐进入视野。前段时间看到本文介绍的相关工作还是MNIST数据集上的实验,现在这个工作推进到BERT上…...
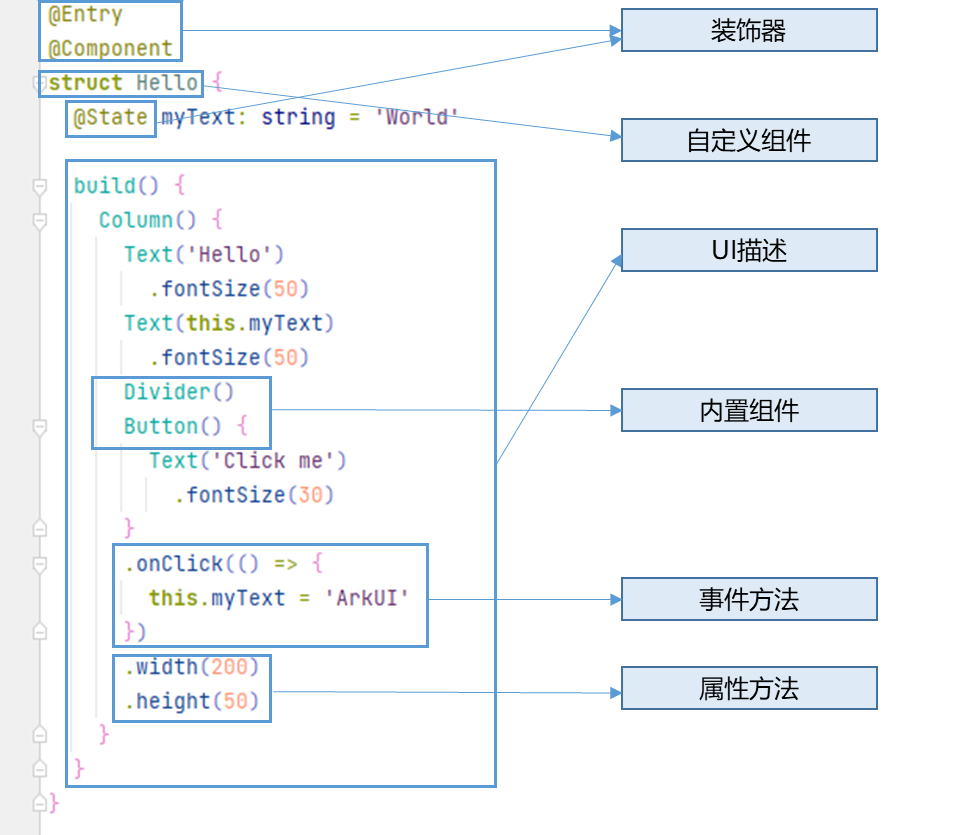
鸿蒙4.0开发笔记之ArkTs语言基础与基本组件结构(四)
文章声明:本文关于HarmonyOS系统的部分内容和描述借鉴于华为官网的“HarmonyOS开发者学堂”,有需要的也可以进入官网查看。<HarmonyOS第一课>ArkTS开发语言介绍 一、ArkTs语言介绍 ArkTS是鸿蒙系统(HarmonyOS)优选的主力应…...

Another app is currently holding the yum lock; waiting for it to exit...
今天使用yum进行下载的时候报错 解决办法: 执行 rm -f /var/run/yum.pid 然后重新运行yum指令即可,发现已经可以正常下载啦!...

size和shape的区别与联系
对于Numpy数据类型 shape和size都是属于Numpy的属性 arr.shape 将返回一个包含两个元素的元组,例如 (m, n),其中 m 表示数组的行数,n 表示数组的列数。arr.size 将返回数组中元素的总数。 举例: 输入: import numpy as np# 创…...
浅谈STL中的分配器
分配器是STL中的六大部件之一,是各大容器能正常运作的关键,但是对于用户而言确是透明的,它似乎更像是一个幕后英雄,永远也不会走到舞台上来,观众几乎看不到它的身影,但是它又如此的重要。作为用户ÿ…...
禁止指定电脑程序运行的2种方法
你可能要问了,为什么要禁止电脑程序运行呢,因为有的公司要净化公司的工作环境,防止某些刺头员工在公司电脑上瞎搞。也有部分家长,是为了防止自己家的孩子利用电脑乱下载东西。 今天就分享2种禁止指定电脑程序运行的方法࿱…...
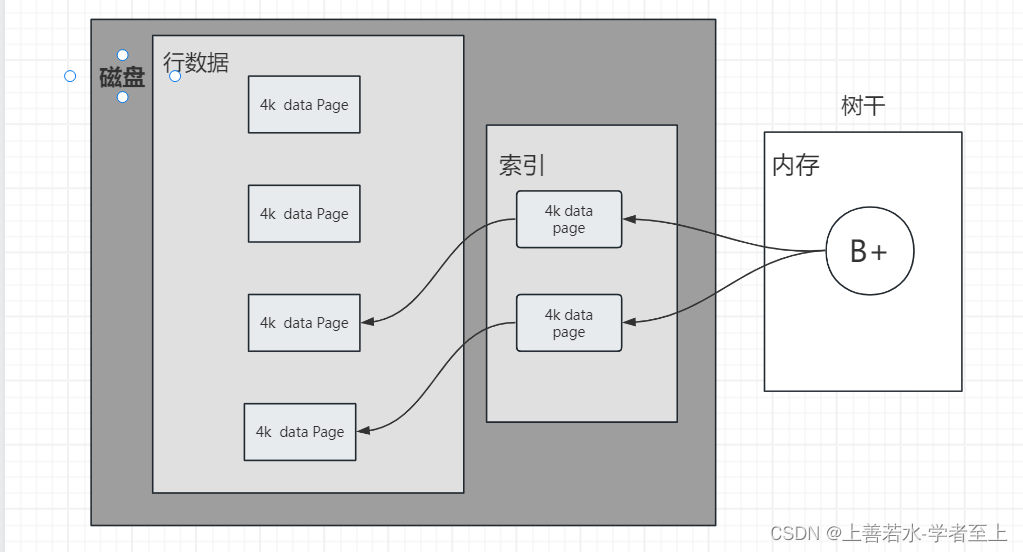
【Redis】前言--redis产生的背景以及过程
一.介绍 为什么会出现Redis这个中间件,从原始的磁盘存储到Redis中间又发生了哪些事,下面进入正题 二.发展史 2.1 磁盘存储 最早的时候都是以磁盘进行数据存储,每个磁盘都有一个磁道。每个磁道有很多扇区,一个扇区接近512Byte。…...

Java面试-微服务篇-SpringCloud
Java面试-微服务篇-SpringCloud SpringCloud 常见组件注册中心Eureka, Nacos负载均衡Ribbon服务雪崩, 熔断降级微服务的监控来源 SpringCloud 常见组件 通常情况下 Eureka: 注册中心Ribbon: 负载均衡Feign: 远程调用Hystrix: 服务熔断Zuul/Gateway: 网关 SpringCloudAlibaba…...
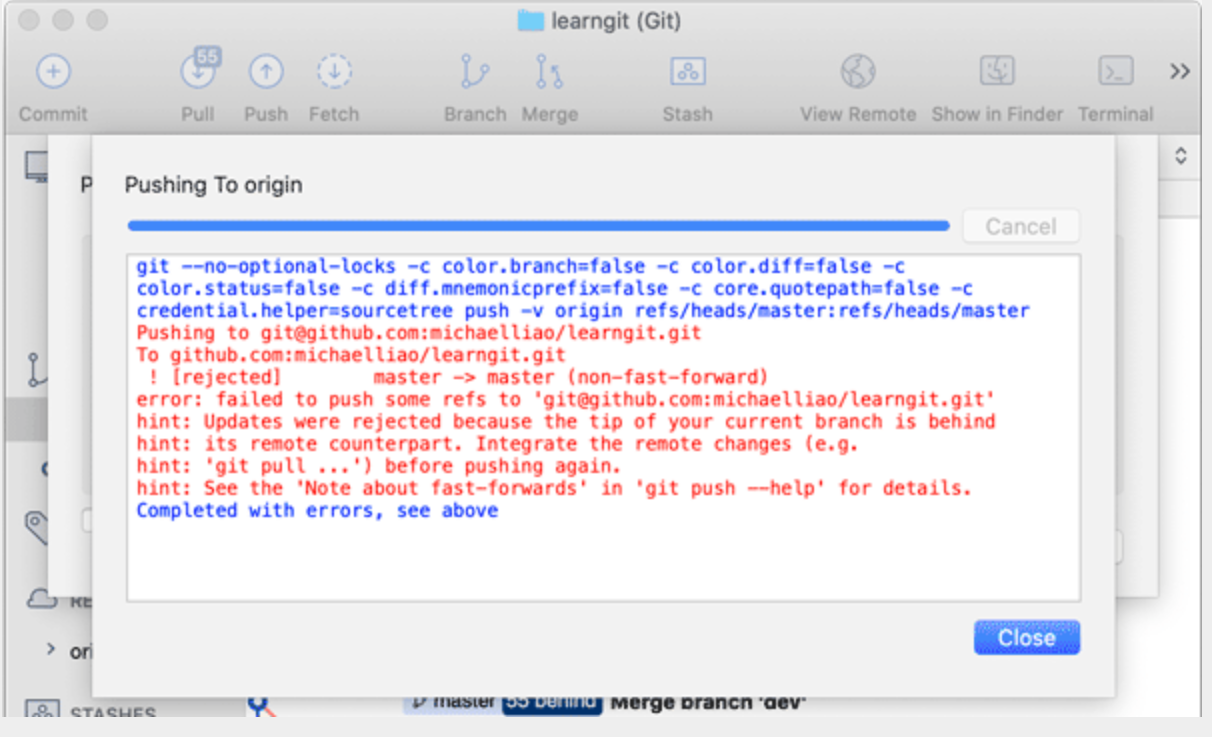
Git使用详解
文章目录 ⭐️写在前面的话⭐️📌What is it?Git的诞生 🌈Why learn it?集中式vs分布式 🧲Who does it?🎈When to use it? And Where to use it?💊How to use it?(重点)1、安装Git在Linux…...
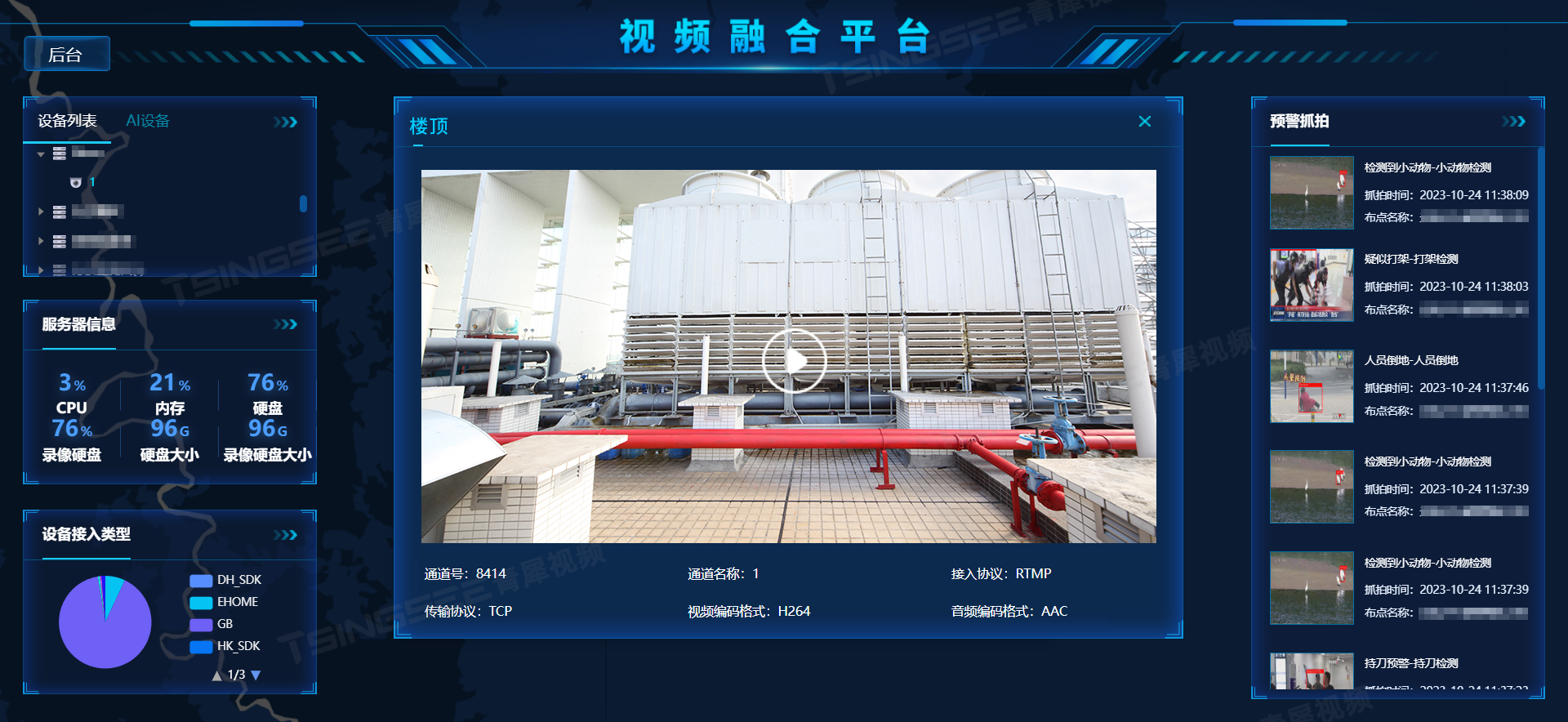
智慧楼宇可视化视频综合管理系统,助力楼宇高效安全运行
随着互联网技术的进步和发展,智能化的楼宇建设也逐步成为人们选择办公场所是否方便的一个重要衡量因素。在智能化楼宇中,安全管理也是重要的一个模块。得益于互联网新兴技术的进步,安防视频监控技术也得到了快速发展并应用在楼宇的安全管理中…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
