管理类联考——数学——汇总篇——知识点突破——代数——函数——记忆
文章目录
- 整体
- 文字提炼
- 图像绘画
- 考点
- 记忆/考点汇总——按大纲
本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多,通常使用记忆宫殿法,绘图记忆法进行记忆,针对局部/细节/组成的部分,可通过多种方法,比如联想记忆法、理解记忆法等进行进一步记忆。
整体
整体使用记忆宫殿法和绘图记忆法等进行记忆
文字提炼
通过目录大纲法和重点归纳法等,进行重要考点的提炼串联
函数、方程、不等式:【函数核心在于图像,图像又涉及交点;方程核心在于根】
第一:从一元二次函数、方程、不等式出发(因为三者知识点最多且互有关联)
1.对于一元二次函数:
【固定做题法:
⟹ \Longrightarrow ⟹ 一看开口方向:(注意自然语言的表达以决定对二次项系数a是否等于0进行分类讨论)二次函数,二次方程,二次不等式,抛物线(默认a≠0);函数,方程,不等式(需要对a是否等于0进行分类讨论)
⟹ \Longrightarrow ⟹ 二看判别式: △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
⟹ \Longrightarrow ⟹ 三看对称轴: x = − b 2 a x=-\frac{b}{2a} x=−2ab
⟹ \Longrightarrow ⟹ 四看交点值:顶点坐标: ( − b 2 a , 4 a c − b 2 4 a ) (-\frac{b}{2a},\frac{4ac-b^2}{4a}) (−2ab,4a4ac−b2)。当 △ = b 2 − 4 a c > 0 △=b^2-4ac>0 △=b2−4ac>0时,函数图象与x轴有两个不同的交点 M 1 ( x 1 , 0 ) , M 2 ( x 2 , 0 ) M_1(x_1,0),M_2(x_2,0) M1(x1,0),M2(x2,0),则 ∣ M 1 M 2 ∣ = ∣ x 1 − x 2 ∣ = △ ∣ a ∣ |M_1M_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|} ∣M1M2∣=∣x1−x2∣=∣a∣△。
】
图像绘画
记忆宫殿法的记忆桩来存放一二级目录,绘图记忆法记忆细节等。
床尾游泳池
U型泳池放置一元二次函数
泳池上部分:有颗苹果
泳池下部:有着顶点,一边是对称轴,一边是y最值。
考点
通过汇总各方大佬资料,作为收集考点/记忆点的信息输入:XX,收集汇总如下:
汇总考点的必要,或者说,汇总记忆的内容的必要,不言而喻,首先,你要记忆东西,得有东西,所以你要梳理出你需要记忆的全部东西,其次,在收集多个大佬的梳理的考点,又可以找出各条逻辑帮助记忆考点,所以,梳理考点是很有必要的,是记忆的基础,是记忆宫殿里面的物品,是我们最后考试需要去找到的解题物品。
记忆/考点汇总——按大纲
——一元二次函数——【图像→交点】
——【 a x 2 + b x + c = y ax^2+bx+c=y ax2+bx+c=y二次函数核心在于“图像”:整体可以由: 图像(形状,上下,交点) ⟹ \Longrightarrow ⟹ △ △ △ ⟹ \Longrightarrow ⟹ 抛物线与x轴交点 ⟹ \Longrightarrow ⟹ 交点图形】
——【固定做题法:
⟹ \Longrightarrow ⟹ 一看开口方向:(注意自然语言的表达以决定对二次项系数a是否等于0进行分类讨论)二次函数,二次方程,二次不等式,抛物线(默认a≠0);函数,方程,不等式(需要对a是否等于0进行分类讨论)
⟹ \Longrightarrow ⟹ 二看判别式: △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
⟹ \Longrightarrow ⟹ 三看对称轴: x = − b 2 a x=-\frac{b}{2a} x=−2ab
⟹ \Longrightarrow ⟹ 四看交点值:顶点坐标: ( − b 2 a , 4 a c − b 2 4 a ) (-\frac{b}{2a},\frac{4ac-b^2}{4a}) (−2ab,4a4ac−b2)。当 △ = b 2 − 4 a c > 0 △=b^2-4ac>0 △=b2−4ac>0时,函数图象与x轴有两个不同的交点 M 1 ( x 1 , 0 ) , M 2 ( x 2 , 0 ) M_1(x_1,0),M_2(x_2,0) M1(x1,0),M2(x2,0),则 ∣ M 1 M 2 ∣ = ∣ x 1 − x 2 ∣ = △ ∣ a ∣ |M_1M_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|} ∣M1M2∣=∣x1−x2∣=∣a∣△。】
1.三种函数形式:
一般式: y = a x 2 + b x + c ( a ≠ 0 ) y=ax^2+bx+c(a≠0) y=ax2+bx+c(a=0)
配方式/顶点式: y = a ( x + b 2 a ) 2 + 4 a c − b 2 4 a y=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a} y=a(x+2ab)2+4a4ac−b2,对称轴为 x = − b 2 a x=-\frac{b}{2a} x=−2ab,顶点坐标为 ( − b 2 a , 4 a c − b 2 4 a ) (-\frac{b}{2a},\frac{4ac-b^2}{4a}) (−2ab,4a4ac−b2)
两根/零点式: y = a ( x − x 1 ) ( x − x 2 ) y=a(x-x_1)(x-x_2) y=a(x−x1)(x−x2), x 1 , x 2 x_1,x_2 x1,x2是函数的两个根,对称轴为 x = x 1 + x 2 2 x=\frac{x_1+x_2}{2} x=2x1+x2
2.图像特点:
图像形状:二次函数 y = a x 2 + b x + c ( a ≠ 0 ) y=ax^2+bx+c(a≠0) y=ax2+bx+c(a=0)的图像是一条抛物线。——【图像的全身】
开口方向:由a决定,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。——【图像的嘴巴】
对称轴:以 x = − b 2 a x=-\frac{b}{2a} x=−2ab为对称轴。——【图像的比例】
顶点坐标: ( − b 2 a , 4 a c − b 2 4 a ) (-\frac{b}{2a},\frac{4ac-b^2}{4a}) (−2ab,4a4ac−b2)。——【图像的头部】
y轴截距:c,c决定抛物线与y轴交点的位置,影响顶点高度。
定义域:一般隐藏在判别式大于等于零中。
最值:当a>0(a<0)时,有最小(大)值 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2,无最大(小)值。——【需验证对称轴是否在定义域内,在则可套用顶点坐标求最值】
单调性:当a>0时,抛物线开口向上,函数在 ( − ∞ , − b 2 a ] (-∞,-\frac{b}{2a}] (−∞,−2ab]上递减,在 [ − b 2 a , + ∞ ) [-\frac{b}{2a},+∞) [−2ab,+∞)上递增,当 x = − b 2 a x=-\frac{b}{2a} x=−2ab时, f ( x ) m i n = 4 a c − b 2 4 a f(x)_{min}=\frac{4ac-b^2}{4a} f(x)min=4a4ac−b2;当 a < 0 a<0 a<0时,抛物线开口向下,函数在 ( − ∞ , − b 2 a ] (-∞,-\frac{b}{2a}] (−∞,−2ab]上递增,在 [ − b 2 a , + ∞ ) [-\frac{b}{2a},+∞) [−2ab,+∞)上递减,当 x = − b 2 a x=-\frac{b}{2a} x=−2ab时, f ( x ) m a x = 4 a c − b 2 4 a f(x)_{max}=\frac{4ac-b^2}{4a} f(x)max=4a4ac−b2。——【】
交点图像:当 △ = b 2 − 4 a c > 0 △=b^2-4ac>0 △=b2−4ac>0时,函数图象与x轴有两个不同的交点 M 1 ( x 1 , 0 ) , M 2 ( x 2 , 0 ) M_1(x_1,0),M_2(x_2,0) M1(x1,0),M2(x2,0),则 ∣ M 1 M 2 ∣ = ∣ x 1 − x 2 ∣ = △ ∣ a ∣ |M_1M_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|} ∣M1M2∣=∣x1−x2∣=∣a∣△。——【图像的内部】
3.参数含义:二次函数 y = a x 2 + b x + c ( a ≠ 0 ) y=ax^2+bx+c(a≠0) y=ax2+bx+c(a=0)
a:当a>0(a<0)时,有最小(大)值 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2,无最大(小)值。
b:影响对称轴位置,因以 x = − b 2 a x=-\frac{b}{2a} x=−2ab为对称轴。——【a,b决定对称轴的位置】
c:代表图像在y轴上的截距(纵截距),影响顶点高度,因顶点坐标为 ( − b 2 a , 4 a c − b 2 4 a ) (-\frac{b}{2a},\frac{4ac-b^2}{4a}) (−2ab,4a4ac−b2)。
4.图像与x轴的位置:
已知函数 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c与x轴交点的个数,可知
(1)若函数与x轴有2个交点,则 a ≠ 0 和△ = b 2 − 4 a c > 0 a≠0和△=b^2-4ac>0 a=0和△=b2−4ac>0;——【【易错点】此类题易忘掉一元二次函数(方程、不等式)的二次项系数不能为0。要使用 △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac,必先看二次项系数是否为0。】
(2)若函数与x轴有1个交点,即抛物线与x轴相切或图像是一条直线,则 a ≠ 0 和△ = b 2 − 4 a c = 0 a≠0和△=b^2-4ac=0 a=0和△=b2−4ac=0;或 a = 0 和 b ≠ 0 a=0和b≠0 a=0和b=0;
(3)若函数与轴没有交点,则 a ≠ 0 和△ = b 2 − 4 a c < 0 a≠0和△=b^2-4ac<0 a=0和△=b2−4ac<0或 a = b = 0 和 c ≠ 0 a=b=0和c≠0 a=b=0和c=0。
(4)图像始终位于x轴上方,则 a > 0 和△ = b 2 − 4 a c < 0 a>0和△=b^2-4ac<0 a>0和△=b2−4ac<0
(5)图像始终位于x轴下方,则 a < 0 和△ = b 2 − 4 a c < 0 a<0和△=b^2-4ac<0 a<0和△=b2−4ac<0
5.图像与一次函数的交点:
二次函数 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c与一次函数 y = k x + m y=kx+m y=kx+m的交点情况有三种,利用数形结合思想,令两函数值相等,得到新的一元二次方程 a x 2 + b x + c − ( k x + m ) = 0 ax^2+bx+c-(kx+m)=0 ax2+bx+c−(kx+m)=0。
(1)2个交点:新的一元二次方程 △> 0 △>0 △>0。
(2)1个交点:①一次函数与二次函致相切,新的一元二次方程 △ = 0 △=0 △=0。特别地,在顶点处相切时, k = 0 k=0 k=0,一次函数为 y = 4 a c − b 2 4 a y=\frac{4ac-b^2}{4a} y=4a4ac−b2。②一次函数垂直于x轴,k不存在。
(3)0个交点:新的一元二次方程 △< 0 △<0 △<0。
6.特殊的抛物线 y = a x 2 + b x + c ( a ≠ 0 ) y=ax^2+bx+c(a≠0) y=ax2+bx+c(a=0)
(1)若 b = 0 b= 0 b=0,则 y = a x 2 + c y=ax^2+c y=ax2+c,抛物线的对称轴为y轴。
(2)若c = 0,则 y = a x 2 + b x y=ax^2+bx y=ax2+bx,抛物线过原点。
(3)若 b = c = 0 b=c=0 b=c=0,则 y = a x 2 y= ax^2 y=ax2,抛物线的对称轴为y轴且过原点。
——其他函数——【记图像可辅助记忆性质】
正比例函数: y = k x ( k ≠ 0 ) y=kx(k≠0) y=kx(k=0),定义域为 R R R,值域为 R R R,单调性为 k > 0 k>0 k>0时,单调递增; k < 0 k<0 k<0时,单调递减,图像是“一条直线”。
反比例函数: y = k x ( k 为常数, k ≠ 0 ) y=\frac{k}{x}(k为常数,k≠0) y=xk(k为常数,k=0),定义域为{ x ∣ x ≠ 0 x|x≠0 x∣x=0},单调性为k>0时,在区间 ( − ∞ , 0 ) , ( 0 , + ∞ ) (-∞,0),(0,+∞) (−∞,0),(0,+∞)上单调递减;k<0时,在区间 ( − ∞ , 0 ) , ( 0 , + ∞ ) (-∞,0),(0,+∞) (−∞,0),(0,+∞)上单调递增,值域为{ y ∣ y ≠ 0 y|y≠0 y∣y=0},图像是“两条圆心对称的圆弧”。
对勾函数: y = x + 1 x y=x+\frac{1}{x} y=x+x1,定义域为{ x ∣ x ≠ 0 x|x≠0 x∣x=0},值域为 ( − ∞ , − 2 ) ∪ ( 2 , + ∞ ) (-∞,-2)∪(2,+∞) (−∞,−2)∪(2,+∞),单调性为在区间 ( − ∞ , − 1 ) , ( 1 , + ∞ ) (-∞,-1),(1,+∞) (−∞,−1),(1,+∞)上单调递增;在区间 ( − 1 , 0 ) , ( 0 , 1 ) (-1,0),(0,1) (−1,0),(0,1)上单调递减,图像是“两条圆心对称的耐特勾”。
指数函数: y = a x ( a > 0 , a ≠ 1 ) y=a^x(a>0,a≠1) y=ax(a>0,a=1),定义域为 ( − ∞ , + ∞ ) (-∞,+∞) (−∞,+∞),值域 ( 0 , + ∞ ) (0,+∞) (0,+∞),单调性为当 a > 1 a>1 a>1时,是增函数;当 0 < a < 1 0<a<1 0<a<1时,是减函数。图像恒过点 ( 0 , 1 ) ,是“一条弧线” (0,1),是“一条弧线” (0,1),是“一条弧线”。——【 a > 0 a>0 a>0和 0 < a < 1 0<a<1 0<a<1两图像形成交叉于 ( 0 , 1 ) (0,1) (0,1)的文字yi乂】——【指数函数的重点有两部分,一部分是图像性质,往往会涉及利用单调性比大小。另一部分是运算性质,考生需要牢记指数函数的运算公式。】
对数函数: y = l o g a x ( a > 0 且 a ≠ 1 ) y=log_ax(a>0且a≠1) y=logax(a>0且a=1),定义域为 ( 0 , + ∞ ) (0,+∞) (0,+∞),值域 全体实数 R 全体实数R 全体实数R,单调性为当 a > 1 a>1 a>1时,是增函数;当 0 < a < 1 0<a<1 0<a<1时,是减函数。图像恒过点 ( 1 , 0 ) ,是“一条弧线” (1,0),是“一条弧线” (1,0),是“一条弧线”。它与 y = a x y=a^x y=ax互为反函数。——【 a > 0 a>0 a>0和 0 < a < 1 0<a<1 0<a<1两图像形成交叉于 ( 1 , 0 ) (1,0) (1,0)的躺着的文字yi乂】——【对数函数的重点有两部分,一部分是图像性质,往往会涉及利用单调性比大小。另一部分是运算性质,考生需要牢记对数函数的运算公式。此外,对数函数有一个最容易设置陷阱的地方就是在对数函数中要求真数部分恒大于0。】
反函数:同底的指数函数 y = a x y=a^x y=ax与对数函数 y = l o g a x y=log_ax y=logax互为反函数。
指数运算: a m ⋅ a n = a m + n a^m·a^n=a^{m+n} am⋅an=am+n; a m ÷ a n = a m − n a^m÷a^n=a^{m-n} am÷an=am−n; ( a m ) n = a m n (a^m)n=a^{mn} (am)n=amn; a 0 = 1 a^0=1 a0=1; a − n = 1 a n a^{-n}=\frac{1}{a^n} a−n=an1; a m n = a m n a^{\frac{m}{n}}=\sqrt[n]{a^m} anm=nam——【指数函数重点=图像+运算】
对数运算:当 a > 0 a>0 a>0且 a ≠ 1 a≠1 a=1时, m > 0 m>0 m>0, n > 0 n>0 n>0,则 l o g 底 真 log_底真 log底真:——【乘除变加减,指数提到前】
指对互换: a b = N a^b=N ab=N ⟺ \Longleftrightarrow ⟺ l o g a N = b ( a > 0 , a ≠ 1 , N > 0 ) log_aN=b(a>0,a≠1,N>0) logaN=b(a>0,a=1,N>0)
同底对数: l o g a M + l o g a N = l o g a ( M N ) log_aM+log_aN=log_a(MN) logaM+logaN=loga(MN);
同底对数: l o g a M − l o g a N = l o g a ( M N ) log_aM-log_aN=log_a(\frac{M}{N}) logaM−logaN=loga(NM);
幂运算: l o g a m b n = n m l o g a b log_{a^m}b^n=\frac{n}{m}log_ab logambn=mnlogab; m = 1 m=1 m=1时, l o g a b n = n l o g a b log_ab^n=nlog_ab logabn=nlogab; m = n m=n m=n时, l o g a m b n = l o g a b log_{a^m}b^n=log_ab logambn=logab; l o g a M n = 1 n l o g a M log_a\sqrt[n]{M}=\frac{1}{n}log_aM loganM=n1logaM;
换底公式: l o g a b = l o g c b l o g c a = l g b l g a = l n b l n a log_ab=\frac{log_cb}{log_ca}=\frac{lgb}{lga}=\frac{lnb}{lna} logab=logcalogcb=lgalgb=lnalnb, l o g a b = 1 l o g b a log_ab=\frac{1}{log_ba} logab=logba1, l o g a M = l o g b M ÷ l o g b a ( b > 0 且 b ≠ 1 ) log_aM=log_bM÷log_ba(b>0且b≠1) logaM=logbM÷logba(b>0且b=1),一般c取10或e。——【换底公式,真数在上,底数在下】
常用对数:以10为底的对数, l o g 10 N log_{10}N log10N,简记为 l g N lgN lgN;
自然对数:以无理数e(e=2.71828…)为底的对数, l o g e N log_eN logeN,简记为 l n N lnN lnN。
特殊对数: l o g a 1 = 0 log_a1=0 loga1=0, l o g a a = 1 log_aa=1 logaa=1, l o g a b ⋅ l o g b a = 1 log_ab·log_ba=1 logab⋅logba=1,负数和零没有对数, a l o g a b = b a^{log_ab}=b alogab=b, l o g a a s = s log_aa^s=s logaas=s——【 a l o g a b = b a^{log_ab}=b alogab=b】
最值函数:
最大值函数: m a x max max{ x , y , z x,y,z x,y,z}表示 x , y , z x,y,z x,y,z中最大的数;本质为: m a x max max{ a , b , c a,b,c a,b,c} ≥ a ≥a ≥a且 m a x max max{ a , b , c a,b,c a,b,c} ≥ b ≥b ≥b且 m a x max max{ a , b , c a,b,c a,b,c} ≥ c ≥c ≥c。对于函数而言, m a x max max{ f ( x ) , g ( x ) f(x),g(x) f(x),g(x)}表示各函数图像中最高的部分。
最小值函数: m i n min min{ x , y , z x,y,z x,y,z}表示 x , y , z x,y,z x,y,z中最小的数。本质为: m i n min min{ a , b , c a,b,c a,b,c} ≤ a ≤a ≤a且 m i n min min{ a , b , c a,b,c a,b,c} ≤ b ≤b ≤b且 m i n min min{ a , b , c a,b,c a,b,c} ≤ c ≤c ≤c。对于函数而言, m i n min min{ f ( x ) , g ( x ) f(x),g(x) f(x),g(x)}表示各函数图像中最低的部分。
对于max函数图像,先画出各函数图像,然后取图像位于上方部分;对于min函数图像,先画出各函数图像,然后取图像位于下方部分。
绝对值函数:
y = ∣ a x + b ∣ y=|ax+b| y=∣ax+b∣先画 y = a x + b y=ax+b y=ax+b的图像,再将x轴下方的图像翻到x轴上方。
y = ∣ a x 2 + b x + c ∣ y=|ax^2+bx+c| y=∣ax2+bx+c∣的图像,再将x轴下方的图像翻到x轴上方。
y = a x 2 + b ∣ x ∣ + c y=ax^2+b|x|+c y=ax2+b∣x∣+c先画 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c的图像,再将y轴左侧图像删掉,替换成y轴右侧对称过来的图像。
∣ a x + b y ∣ = c b |ax+by|=cb ∣ax+by∣=cb表示两条平行的直线 a x + b y = ± c ax+by=±c ax+by=±c,且两者关于原点对称。
∣ a x ∣ + ∣ b y ∣ = c |ax|+|by|=c ∣ax∣+∣by∣=c,当 a = b a=b a=b时,表示正方形,当 a ≠ b a≠b a=b时,表示菱形。
∣ x y ∣ + a b = a ∣ x ∣ + b ∣ y ∣ |xy|+ab=a|x|+b|y| ∣xy∣+ab=a∣x∣+b∣y∣, ∣ x y ∣ + a b = a ∣ x ∣ + b ∣ y ∣ |xy|+ab=a|x|+b|y| ∣xy∣+ab=a∣x∣+b∣y∣ ⟹ \Longrightarrow ⟹ ∣ x y ∣ − a ∣ x ∣ − b ∣ y ∣ + a b = 0 |xy|-a|x|-b|y|+ab=0 ∣xy∣−a∣x∣−b∣y∣+ab=0 ⟹ \Longrightarrow ⟹ ∣ x ∣ ( ∣ y ∣ − a ) − b ( ∣ y ∣ − a ) = 0 |x|(|y|-a)-b(|y|-a)=0 ∣x∣(∣y∣−a)−b(∣y∣−a)=0 ⟹ \Longrightarrow ⟹ ( ∣ x ∣ − b ) ( ∣ y ∣ − a ) = 0 (|x|-b)(|y|-a)=0 (∣x∣−b)(∣y∣−a)=0 ⟹ \Longrightarrow ⟹ ∣ x ∣ = b |x|=b ∣x∣=b或 ∣ y ∣ = a |y|=a ∣y∣=a, 故表示由 x = ± b , y = ± a x=±b,y=±a x=±b,y=±a围成的图形,当 a = b a=b a=b时,表示正方形,当 a ≠ b a≠b a=b时,表示矩形。
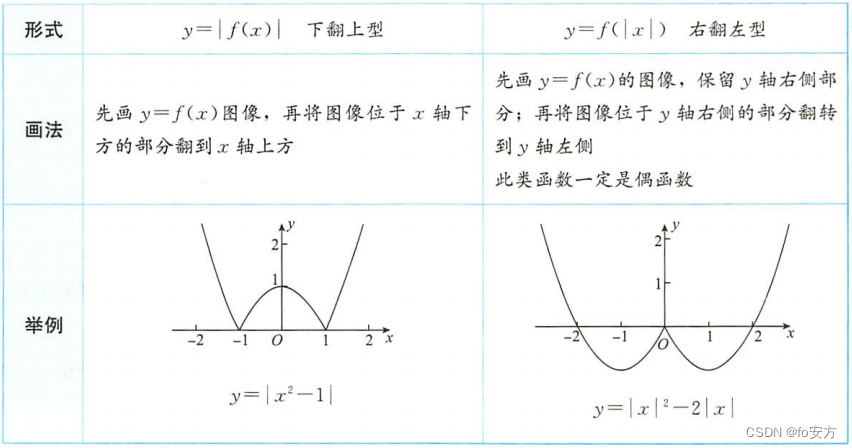
y = ∣ f ( x ) ∣ y=|f(x)| y=∣f(x)∣上翻下型:先画 y = f ( x ) y=f(x) y=f(x)图像,再将图像位于x轴下方的部分翻到x轴上方。
y = f ( ∣ x ∣ ) y=f(|x|) y=f(∣x∣)右翻左型:先画 y = f ( x ) y=f(x) y=f(x)的图像,保留y轴右侧部分;再将右侧的部分翻转到y轴左侧。
分段函数:
分段函数:对于其定义域内的自变量x的不同值,不能用一个统一的解析式表示,而是要用两个或两个以上的式子表示。分段函数表示不同的取值范围对应不同的表达式。对于分段函数,根据不同取值区间,选择不同的表达式代入求解。
模型识别:自变量在不同取值范围内有不同的对应法则。
解题方法:求分段函数的函数值 f ( x 0 ) f(x_0) f(x0)时,应该首先判断 x 0 x_0 x0所属的取值范围,然后把 x 0 x_0 x0代入到相应的解析式中进行计算。
思路:分段函数是指自变量在两个或两个以上不同的范围内,有不同的对应法则的函数。它是一个函数,是一类表达形式特殊的函数,却又常常被学生误认为是几个函数。它的定义城是各段函数定义域的并集,其值域也是各段函数值城的并集。分段函数有关问题蕴含着分类讨论、数形结合等思想方法。分段函数应用较广,做题时要根据范围来确定对应的表达式。
复合函数:
(1)定义:已知函数 y = f ( u ) y=f(u) y=f(u),又 u = g ( x ) u=g(x) u=g(x),则称函数 y = f ( g ( x ) ) y=f(g(x)) y=f(g(x))为函数 y = f ( u ) y =f(u) y=f(u)与 u = g ( x ) u =g(x) u=g(x)的复合函数。其中y称为因变量,x称为自变量,u称为中间变量。
(2)求复合函数的定义域
①复合函数的定义域,是函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]中x的取值范围;
②若函数 f ( x ) f(x) f(x)的定义域为 ( a , b ) (a,b) (a,b),则复合函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]的定义域由 a < g ( x ) < b a<g(x)<b a<g(x)<b求出;
③若函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]的定义域为 ( a , b ) (a,b) (a,b),则 f ( x ) f(x) f(x)的定义域为 g ( x ) g(x) g(x)在 a < x < b a<x<b a<x<b上的值域。
注意: g ( x ) g(x) g(x)的值域对应 y = f ( u ) y=f(u) y=f(u)的定义域。对于复合函数,可以将内部的函数看成一个整体进行分析。此外,内部函数的值域对应外部函数的定义域。
(3)复合函数的单调性——【同增异减】
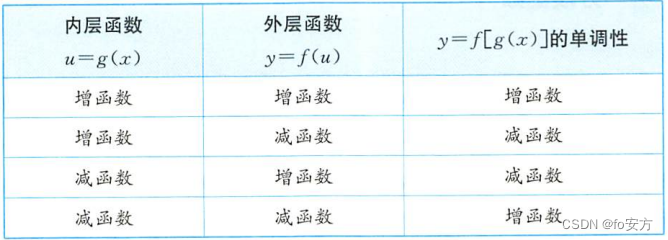
奇偶函数:
① 奇函数的性质
定义域关于原点对称,图像关于原点对称: f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x)
② 偶函数的性质
定义域关于原点对称,图像关于y轴对称: f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x)
反比例函数: y = k x ( k ≠ 0 ) y=\frac{k}{x}(k≠0) y=xk(k=0)
在一个反比例函数图像上任取一点,过该点分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为 ∣ k ∣ |k| ∣k∣。

相关文章:

管理类联考——数学——汇总篇——知识点突破——代数——函数——记忆
文章目录 整体文字提炼图像绘画 考点记忆/考点汇总——按大纲 本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多&am…...
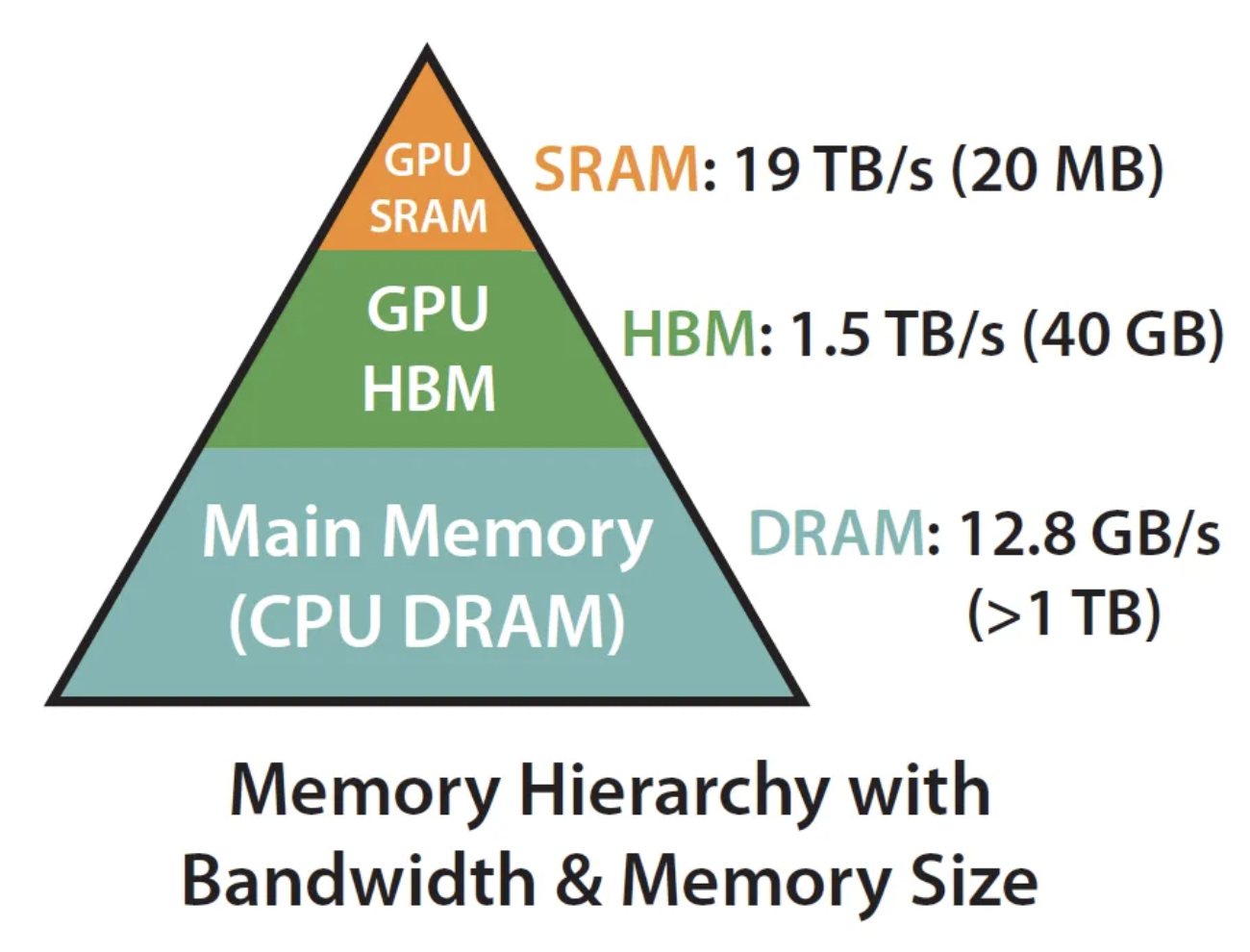
Flash Attention:高效注意力机制的突破与应用
注意力机制彻底改变了自然语言处理和深度学习领域。它们允许模型在执行机器翻译、语言生成等任务时专注于输入数据的相关部分。 在这篇博客[1]中,我们将深入研究被称为“Flash Attention”的注意力机制的突破性进展。我们将探讨它是什么、它是如何工作的,…...

Flutter开发警告Constructors in ‘@immutable‘ classes should be declared as ‘const‘
文章目录 警告信息报错代码警告原因修改后的代码 警告信息 Flutter开发遇到如下警告 Constructors in ‘immutable’ classes should be declared as ‘const’. 报错代码 class TaskWidget extends StatefulWidget {final String title;final bool isChecked;final int ord…...

想当老师应该去学什么专业
专业选择是决定未来职业发展的重要步骤,如果你也想成为一名老师,那么这五个专业可能会适合你! 教育学专业 教育学专业是培养教育理论和方法的学科,这些理论知识将帮助你理解教学过程、学生发展、课程设计和评估。该专业将让你全面…...
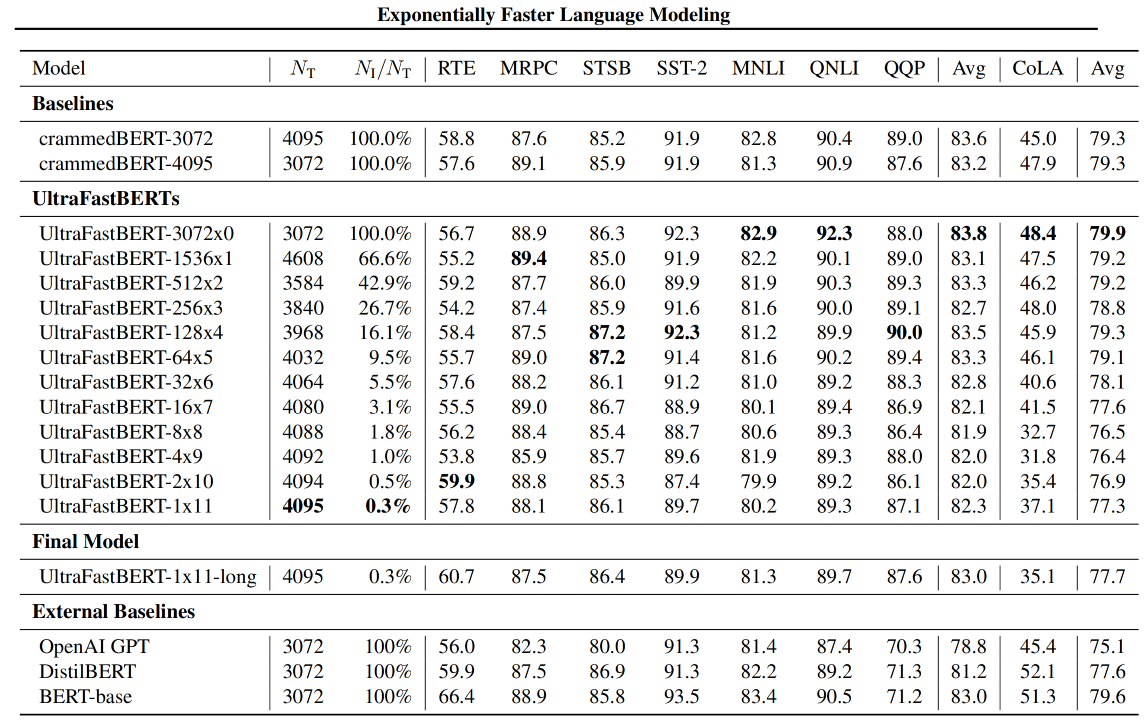
【LM、LLM】浅尝二叉树在前馈神经网络上的应用
前言 随着大模型的发展,模型参数量暴涨,以Transformer的为组成成分的隐藏神经元数量增长的越来越多。因此,降低前馈层的推理成本逐渐进入视野。前段时间看到本文介绍的相关工作还是MNIST数据集上的实验,现在这个工作推进到BERT上…...
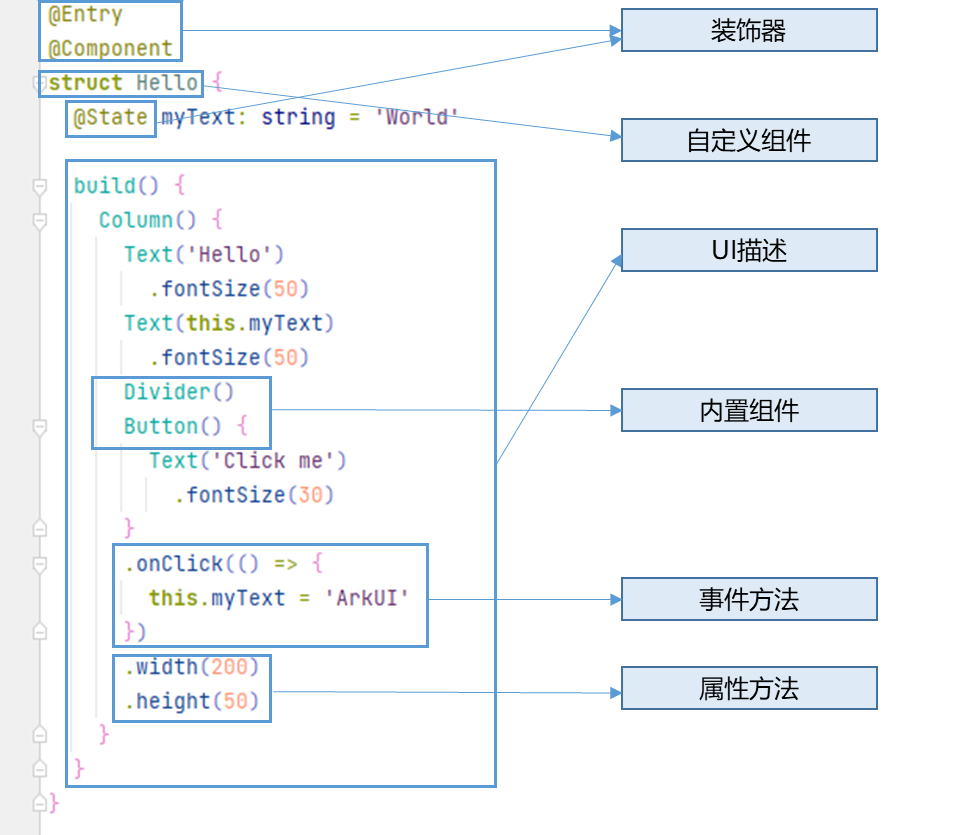
鸿蒙4.0开发笔记之ArkTs语言基础与基本组件结构(四)
文章声明:本文关于HarmonyOS系统的部分内容和描述借鉴于华为官网的“HarmonyOS开发者学堂”,有需要的也可以进入官网查看。<HarmonyOS第一课>ArkTS开发语言介绍 一、ArkTs语言介绍 ArkTS是鸿蒙系统(HarmonyOS)优选的主力应…...

Another app is currently holding the yum lock; waiting for it to exit...
今天使用yum进行下载的时候报错 解决办法: 执行 rm -f /var/run/yum.pid 然后重新运行yum指令即可,发现已经可以正常下载啦!...

size和shape的区别与联系
对于Numpy数据类型 shape和size都是属于Numpy的属性 arr.shape 将返回一个包含两个元素的元组,例如 (m, n),其中 m 表示数组的行数,n 表示数组的列数。arr.size 将返回数组中元素的总数。 举例: 输入: import numpy as np# 创…...
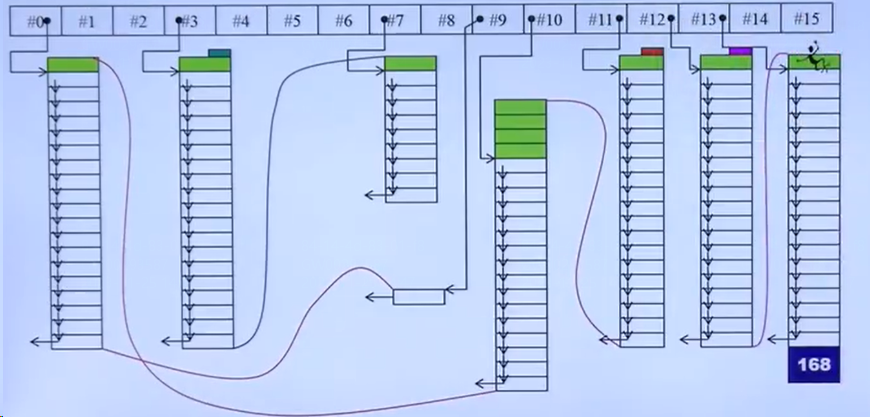
浅谈STL中的分配器
分配器是STL中的六大部件之一,是各大容器能正常运作的关键,但是对于用户而言确是透明的,它似乎更像是一个幕后英雄,永远也不会走到舞台上来,观众几乎看不到它的身影,但是它又如此的重要。作为用户ÿ…...
禁止指定电脑程序运行的2种方法
你可能要问了,为什么要禁止电脑程序运行呢,因为有的公司要净化公司的工作环境,防止某些刺头员工在公司电脑上瞎搞。也有部分家长,是为了防止自己家的孩子利用电脑乱下载东西。 今天就分享2种禁止指定电脑程序运行的方法࿱…...
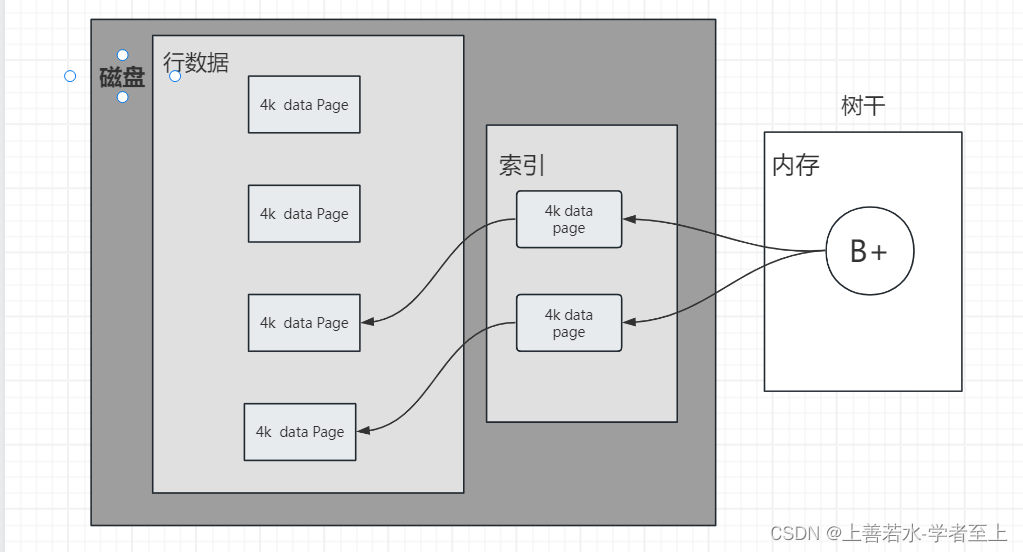
【Redis】前言--redis产生的背景以及过程
一.介绍 为什么会出现Redis这个中间件,从原始的磁盘存储到Redis中间又发生了哪些事,下面进入正题 二.发展史 2.1 磁盘存储 最早的时候都是以磁盘进行数据存储,每个磁盘都有一个磁道。每个磁道有很多扇区,一个扇区接近512Byte。…...

Java面试-微服务篇-SpringCloud
Java面试-微服务篇-SpringCloud SpringCloud 常见组件注册中心Eureka, Nacos负载均衡Ribbon服务雪崩, 熔断降级微服务的监控来源 SpringCloud 常见组件 通常情况下 Eureka: 注册中心Ribbon: 负载均衡Feign: 远程调用Hystrix: 服务熔断Zuul/Gateway: 网关 SpringCloudAlibaba…...
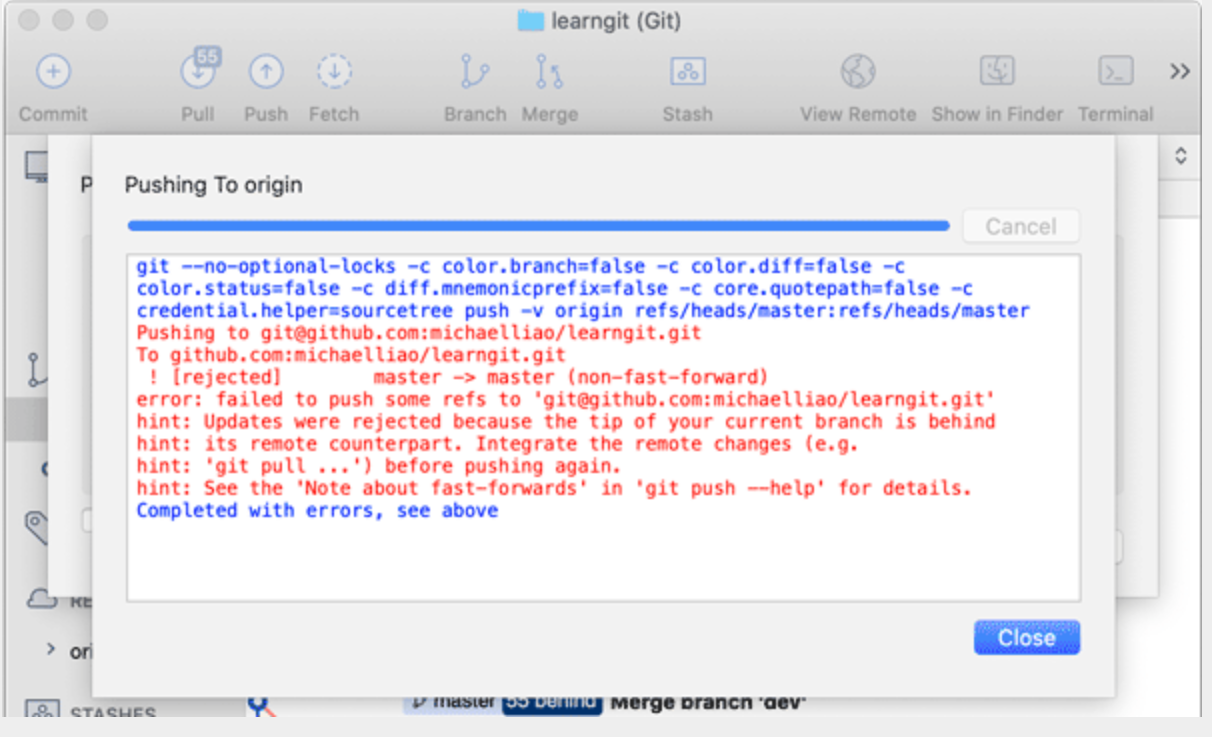
Git使用详解
文章目录 ⭐️写在前面的话⭐️📌What is it?Git的诞生 🌈Why learn it?集中式vs分布式 🧲Who does it?🎈When to use it? And Where to use it?💊How to use it?(重点)1、安装Git在Linux…...
智慧楼宇可视化视频综合管理系统,助力楼宇高效安全运行
随着互联网技术的进步和发展,智能化的楼宇建设也逐步成为人们选择办公场所是否方便的一个重要衡量因素。在智能化楼宇中,安全管理也是重要的一个模块。得益于互联网新兴技术的进步,安防视频监控技术也得到了快速发展并应用在楼宇的安全管理中…...

【opencv】计算机视觉:实时目标追踪
目录 前言 解析 深入探究 前言 目标追踪技术对于民生、社会的发展以及国家军事能力的壮大都具有重要的意义。它不仅仅可以应用到体育赛事当中目标的捕捉,还可以应用到交通上,比如实时监测车辆是否超速等!对于国家的军事也具有一定的意义&a…...

生态对对碰|华为OceanStor闪存存储与OceanBase完成兼容性互认证!
近日,北京奥星贝斯科技有限公司 OceanBase 数据库与华为技术有限公司 OceanStor Dorado 全闪存存储系统、OceanStor 混合闪存存储系统完成兼容性互认证。 OceanBase 数据库挂载 OceanStor 闪存存储做为数据盘和日志盘,在 OceanStor 闪存存储系统卓越性能…...

微服务负载均衡器Ribbon
1.什么是Ribbon 目前主流的负载方案分为以下两种: 集中式负载均衡,在消费者和服务提供方中间使用独立的代理方式进行负载,有硬件的(比如 F5),也有软件的(比如 Nginx)。 客户端根据…...
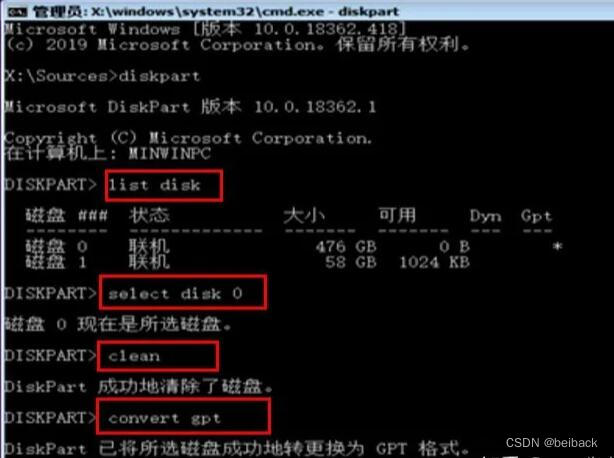
win10戴尔电脑安装操作系统遇到的问题MBR分区表只能安装GPT磁盘
首先按F2启动boot管理界面 调整启动盘的启动顺序,这里启动U盘为第一顺序。 第一步 选择安装程序的磁盘 第二步 转换磁盘为GPT磁盘 一般出现 磁盘0和1,说明存在两个盘 ,这里两个盘不是说的是C盘和D盘的问题,而是在物理上实际存在…...

阿里云服务器(vgn7i-vws) anaconda(py39)+pytorch1.12.0(cu113)
用xshell连接ip地址,端口号22,输入用户密码 安装anaconda 2022 10 py3.9 wget https://repo.anaconda.com/archive/Anaconda3-2022.10-Linux-x86_64.sh sha256sum Anaconda3-2022.10-Linux-x86_64.sh #校验数据完整性 chmod ux Anaconda3-2022.10-…...

使用 STM32F7 和 TensorFlow Lite 开发低功耗人脸识别设备
本文旨在介绍如何使用 STM32F7 和 TensorFlow Lite框架开发低功耗的人脸识别设备。首先,我们将简要介绍 STM32F7 的特点和能力。接下来,我们将讨论如何使用 TensorFlow Lite 在 STM32F7 上实现人脸识别算法。然后,我们将重点关注如何优化系统…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
