强化学习,快速入门与基于python实现一个简单例子(可直接运行)
文章目录
- 一、什么是“强化学习”
- 二、强化学习包括的组成部分
- 二、Q-Learning算法
- 三、迷宫-强化学习-Q-Learning算法的实现
- 全部代码(复制可用)
- 可用状态空间
- 检查是否超出边界
- epsilon 的含义
- 更新方程
- 总结
一、什么是“强化学习”
本文要记录的大概内容:
强化学习是一种机器学习方法,旨在让智能体通过与环境的交互学习如何做出最优决策以最大化累积奖励。在强化学习中,智能体通过尝试不同的行动并观察环境的反馈(奖励或惩罚)来学习。它不依赖于预先标记的训练数据,而是通过与环境的实时交互进行学习。
强化学习的核心概念包括以下几个要素:
智能体(Agent):执行动作并与环境进行交互的学习主体。
环境(Environment):智能体所处的外部环境,它对智能体的动作做出反应,并提供奖励或惩罚信号。
状态(State):在特定时间点,环境所处的情境或配置,用于描述环境的特征。
动作(Action):智能体在某个状态下可以执行的操作或决策。
奖励(Reward):环境根据智能体的动作提供的反馈信号,用于评估动作的好坏。
策略(Policy):智能体采取行动的方式或决策规则,它映射状态到动作的选择。
价值函数(Value Function):评估在特定状态下采取特定动作的长期价值或预期回报。
Q值(Q-Value):表示在给定状态下采取特定动作的预期回报值。
强化学习的目标是通过学习最优策略或价值函数来使智能体能够在不同的状态下做出最佳决策,以最大化累积奖励。学习过程通常使用基于迭代的方法,例如Q-learning、SARSA、深度强化学习等。强化学习在许多领域具有广泛的应用,包括自动驾驶、机器人控制、游戏智能以及优化和决策问题等。
以下是本篇文章正文内容
二、强化学习包括的组成部分
当涉及到设计一个完整的强化学习过程时,需要考虑多个方面,包括环境、代理程序、奖励函数、状态空间、动作空间等。为了提供一个简单而完整的示例,下面以设计一个基于强化学习的迷宫求解问题为例进行分析:
环境 Environment:
我们选择一个简单的方格迷宫作为环境。迷宫由多个方格组成,其中包括起点和终点。
迷宫中可能存在障碍物,代表着无法通过的区域。
环境会提供代理程序当前的状态信息,并接受代理程序的动作。
代理程序 Agent:
代理程序就是智能体,就是我们所设计算法
我们设计一个简单的代理程序,它会根据当前的状态选择一个动作。
代理程序将使用强化学习算法来学习如何在迷宫中移动,以找到终点。
在这个示例中,我们将使用Q-learning算法作为强化学习算法。
状态空间 state_space:
状态空间定义了代理程序可能处于的不同状态。在迷宫中,状态可以表示为当前的位置坐标。
动作空间定义了代理程序可以执行的不同动作。
动作空间 action_space:
在迷宫中,可选的动作可以是上、下、左、右四个方向的移动。
奖励函数 reward:
我们定义奖励函数来指导代理程序的学习过程。
当代理程序达到终点时,奖励为正值,表示取得了成功。
当代理程序遇到障碍物时,奖励为负值,表示不可行的移动。
其他情况下,奖励为零。
这是一个基本的强化学习过程的设计示例。要使其运行,需要实现Q-learning算法和迷宫环境的交互逻辑,并根据定义的状态空间、动作空间和奖励函数进行训练和学习,下面介绍Q-Learning算法。
二、Q-Learning算法
Q-Learning(Q学习)是一种强化学习算法,用于解决马尔可夫决策过程(MDP)。它是一种无模型算法,意味着它不需要显式地了解环境动态。Q-Learning的目标是学习一个最优的动作值函数,称为Q函数,它表示在给定状态下采取特定动作的预期累积奖励。Q-Learning的主要目标是学习一个能够最大化累积奖励的策略。
注意: 传统的Q-Learning算法不涉及深度学习的知识
以下是Q-Learning算法的详细步骤:
-
初始化:对所有状态(s)和动作(a),使用任意值初始化Q函数,记作Q(s, a)。通常,Q函数以表格或矩阵的形式表示。
-
探索与利用:选择在当前状态下执行的动作。在探索与利用之间存在一个权衡。初期通常会更多地进行探索,以便探索不同的状态和动作,随着学习的进行逐渐增加利用已知的高价值动作。
-
执行动作:根据选择的动作,与环境进行交互,观察下一个状态(s’)和获得的即时奖励(r)。
-
更新Q函数:使用Q-Learning更新Q函数的值。根据观察到的即时奖励和下一个状态的最大Q值,更新当前状态和动作的Q值。更新公式为:Q(s, a) = (1 - α) * Q(s, a) + α * (r + γ * max(Q(s’, a’))),其中α是学习率(控制新信息的重要性),γ是折扣因子(控制未来奖励的重要性)。
-
转移到下一个状态:将当前状态更新为下一个状态,继续执行步骤2-4,直到达到终止状态或达到指定的停止条件。
-
收敛:通过不断地与环境交互和更新Q函数,最终Q函数会收敛到最优的动作值函数,表示了在每个状态下采取最佳动作的预期累积奖励。
Q-Learning算法的核心思想是基于试错学习,通过与环境的交互不断优化动作策略,以获得最大的累积奖励。通过迭代更新Q函数,Q-Learning能够学习到最优的策略,从而在复杂的环境中实现自主决策。
三、迷宫-强化学习-Q-Learning算法的实现
全部代码(复制可用)
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import joblib# 定义迷宫环境
class MazeEnvironment:def __init__(self):self.grid = np.array([[0, 0, 0, 0, 0],[0, -1, -1, -1, 0],[0, 0, 0, 0, 0],[0, -1, -1, -1, 1],[0, 0, 0, 0, 0]]) # 0表示可通过的空格,-1表示障碍物,1表示目标self.state_space = np.argwhere(self.grid == 0).tolist() # 可用的状态空间self.victory = np.argwhere(self.grid == 1).tolist()self.state_space.extend(self.victory) # # 最终可用的状态空间self.action_space = ['up', 'down', 'left', 'right'] # 动作空间self.num_states = len(self.state_space)self.num_actions = len(self.action_space)self.current_state = Nonedef reset(self):self.current_state = [0, 0] # 设置起始状态return self.current_statedef step(self, action):if action == 'up':next_state = [self.current_state[0] - 1, self.current_state[1]]elif action == 'down':next_state = [self.current_state[0] + 1, self.current_state[1]]elif action == 'left':next_state = [self.current_state[0], self.current_state[1] - 1]elif action == 'right':next_state = [self.current_state[0], self.current_state[1] + 1]# 检查下一个状态是否合法if (next_state[0] < 0or next_state[0] >= self.grid.shape[0]or next_state[1] < 0or next_state[1] >= self.grid.shape[1]or self.grid[tuple(next_state)] == -1):next_state = self.current_state# 判断是否到达目标状态done = (self.grid[tuple(next_state)] == 1)self.current_state = next_statereturn next_state, int(done)# 定义强化学习代理程序
class QAgent:def __init__(self, state_space, action_space):self.state_space = state_spaceself.action_space = action_spaceself.num_states = len(state_space)self.num_actions = len(action_space)self.q_table = np.zeros((self.num_states, self.num_actions))def choose_action(self, state, epsilon=0.1):if np.random.uniform(0, 1) < epsilon:action = np.random.choice(self.action_space)else:state_idx = self.state_space.index(state)q_values = self.q_table[state_idx]max_q = np.max(q_values)max_indices = np.where(q_values == max_q)[0]action_idx = np.random.choice(max_indices)action = self.action_space[action_idx]return actiondef update_q_table(self, state, action, next_state, reward, learning_rate, discount_factor):state_idx = self.state_space.index(state)next_state_idx = self.state_space.index(next_state)q_value = self.q_table[state_idx, self.action_space.index(action)]max_q = np.max(self.q_table[next_state_idx])new_q = q_value + learning_rate * (reward + discount_factor * max_q - q_value)self.q_table[state_idx, self.action_space.index(action)] = new_q# 训练强化学习代理程序
def train_agent(agent, environment, num_episodes, learning_rate, discount_factor, epsilon):for episode in range(num_episodes):state = environment.reset()done = Falsewhile not done:action = agent.choose_action(state, epsilon)next_state, reward = environment.step(action)# 更新 Q 值表agent.update_q_table(state, action, next_state, reward, learning_rate, discount_factor)state = next_state # 更新当前状态为下一个状态if reward == 1: # 到达目标状态,结束当前回合done = Truejoblib.dump(agent, './Agent.agt') # 保存智能体# 创建迷宫环境实例
maze_env = MazeEnvironment()# 创建强化学习代理实例
agent = QAgent(maze_env.state_space, maze_env.action_space)# 训练强化学习代理
num_episodes = 1000
learning_rate = 0.1
discount_factor = 0.9
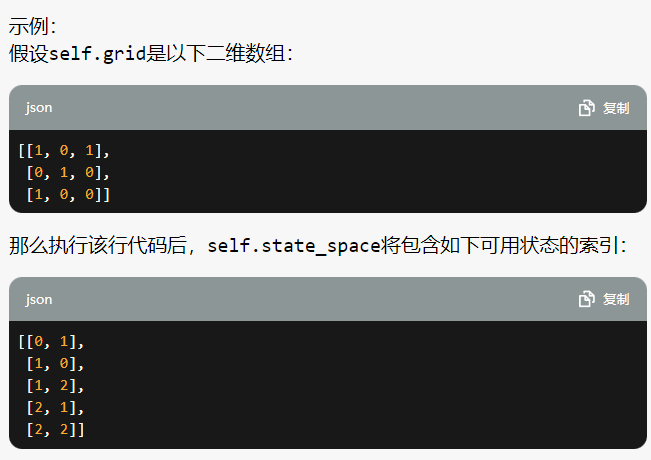
epsilon = 0.1 # 在强化学习中,ε(epsilon)通常用于控制智能体在选择动作时的探索与利用的平衡。train_agent(agent, maze_env, num_episodes, learning_rate, discount_factor, epsilon)可用状态空间
self.state_space = np.argwhere(self.grid == 0).tolist()
检查是否超出边界

epsilon 的含义
在强化学习中,ε(epsilon)通常用于控制智能体在选择动作时的探索与利用的平衡。
ε-greedy策略是一种常见的动作选择策略,其中ε表示以随机动作进行探索的概率,而1-ε表示以具有最高Q值的动作进行利用的概率。
具体含义如下:
当随机数小于ε时,智能体会随机选择一个动作,以便在尚未探索或不确定的状态下进行探索。这有助于发现新的、可能更好的动作。
当随机数大于或等于ε时,智能体会选择具有最高Q值的动作,以利用已经学到的知识和经验。
ε的取值范围通常为0到1之间,根据具体问题和需求进行调整。较小的ε值会更倾向于利用已知的最优动作,而较大的ε值会更倾向于探索未知的动作。
需要注意的是
在训练初期,智能体通常会更多地进行探索,因此ε的初始值可能会较高,随着训练的进行逐渐减小,以便智能体更多地进行利用。
示例:
假设ε的值为0.2,即以20%的概率进行随机动作选择,80%的概率进行利用。
在某个状态下,智能体根据ε-greedy策略进行动作选择:
如果随机数小于0.2,智能体会以20%的概率随机选择一个动作进行探索。
如果随机数大于等于0.2,智能体会以80%的概率选择具有最高Q值的动作进行利用。
通过调整ε的值,可以在探索与利用之间找到适当的平衡,以使智能体能够有效地学习和提高性能。
更新方程
new_q = q_value + learning_rate * (reward + discount_factor * max_q - q_value)
self.q_table[state_idx, self.action_space.index(action)] = new_q
这行代码使用贝尔曼方程更新当前状态和动作对应的Q值。贝尔曼方程表示当前状态和动作的Q值等于当前收益加上折扣因子乘以下一个状态的最大Q值,再减去当前状态和动作的Q值。学习率乘以这个差值,控制了新Q值的更新速度。最后,将更新后的Q值存储回Q表中,以便在后续的训练中使用。
总结
无
相关文章:

强化学习,快速入门与基于python实现一个简单例子(可直接运行)
文章目录 一、什么是“强化学习”二、强化学习包括的组成部分二、Q-Learning算法三、迷宫-强化学习-Q-Learning算法的实现全部代码(复制可用)可用状态空间检查是否超出边界epsilon 的含义更新方程 总结 一、什么是“强化学习” 本文要记录的大概内容&am…...
【手写实现一个简单版的Dubbo,深刻理解RPC框架的底层实现原理】
手写实现一个简单版的Dubbo,深刻理解RPC框架的底层实现原理 RPC框架简介了解Dubbo的实现原理服务暴露服务引入服务调用 手写实现一个简单版的Dubbo服务暴露ServiceBeanProxyFactory#getInvokerProtocol#exportRegistryProtocol#export 服务引入RegistryProto#referD…...
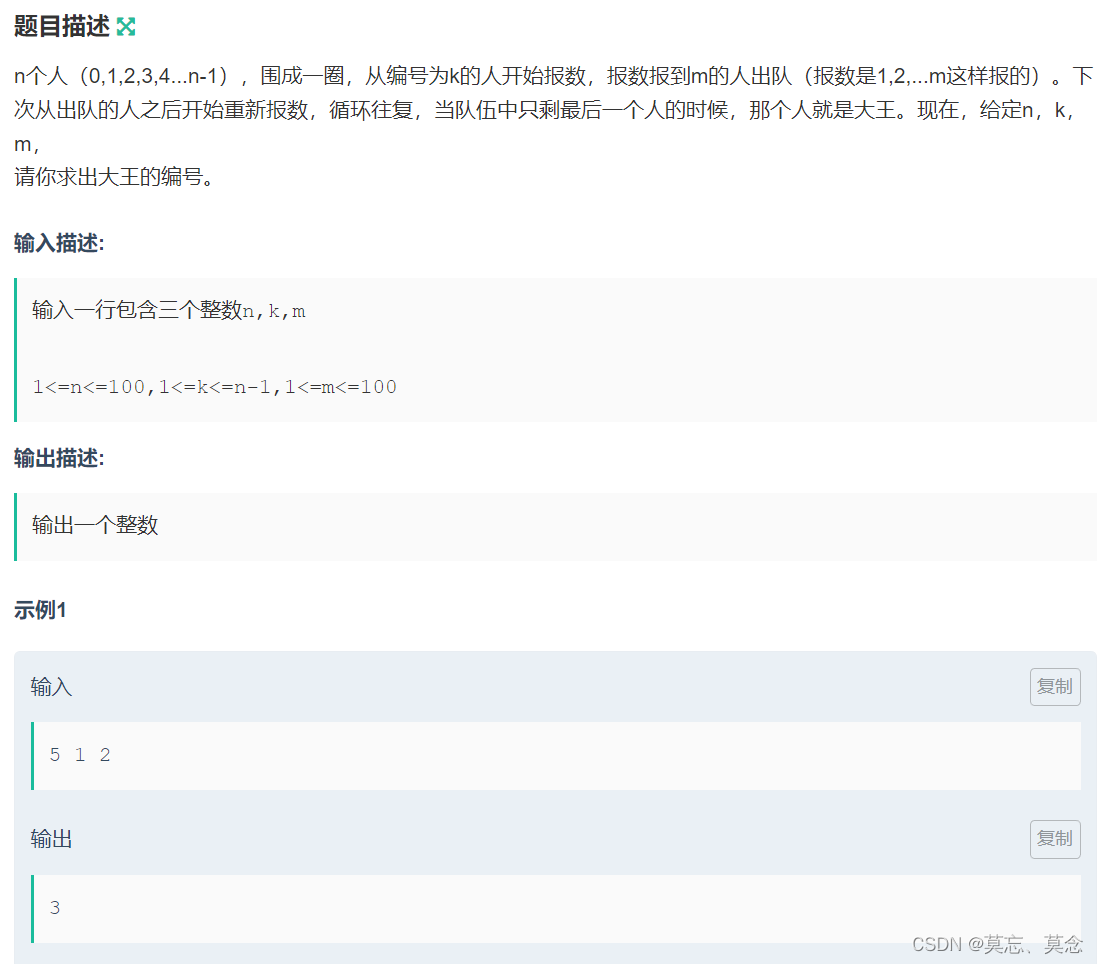
计数问题+约瑟夫问题(map)
目录 一、计数问题 二、约瑟夫问题 一、计数问题 #include<iostream> #include<map> using namespace std; int main() {int n,x;cin>>n>>x;map<int,int>m;for(int i1;i<n;i){if(i>1 && i<10){m[i];}else{int temp i;while (…...

Maven聚合项目发布至私服指定模块
无论是从事框架开发工作还是公共服务模块开发,为了解决通用性问题,常常需要发布一些依赖组件至maven私服。然而通常我们得maven工程都是由多个模块组成得聚合工程(一个父工程下有多个模块)。 这个时候可能会面临两个窘境…...
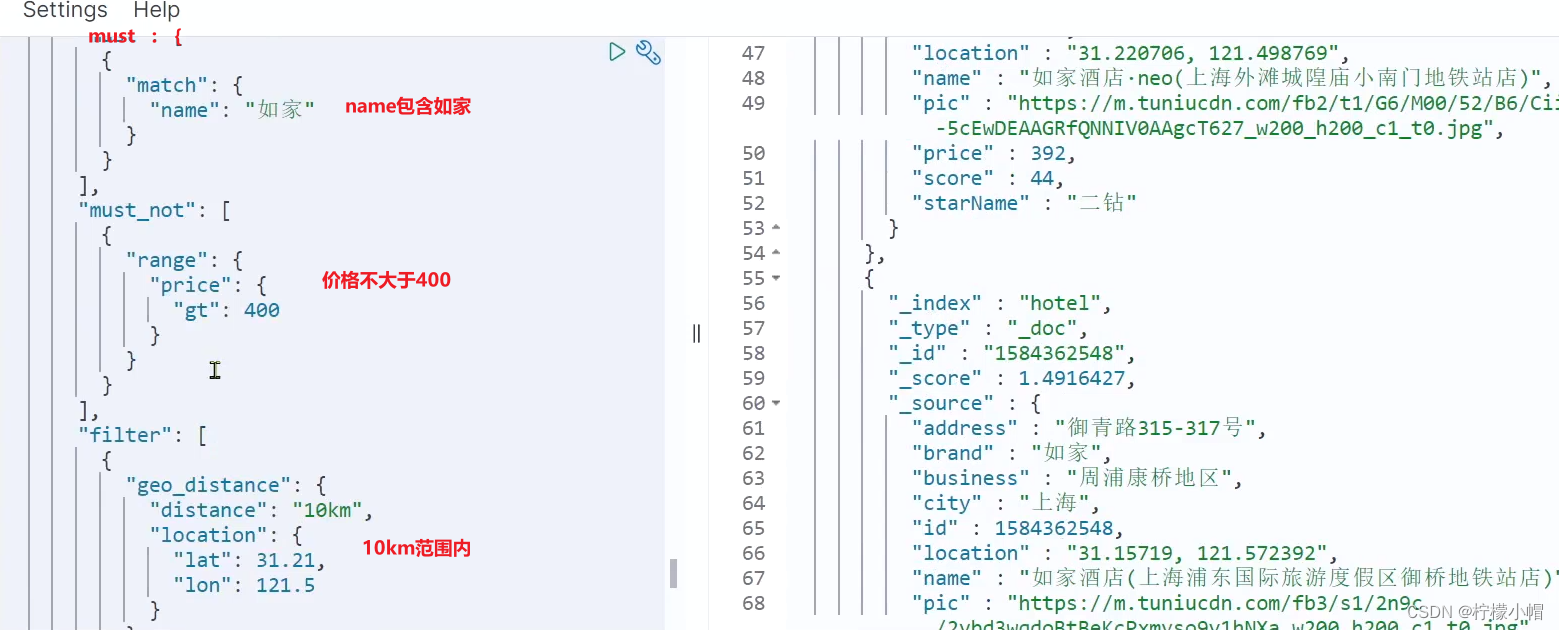
SpringCloud 微服务全栈体系(十六)
第十一章 分布式搜索引擎 elasticsearch 六、DSL 查询文档 elasticsearch 的查询依然是基于 JSON 风格的 DSL 来实现的。 1. DSL 查询分类 Elasticsearch 提供了基于 JSON 的 DSL(Domain Specific Language)来定义查询。常见的查询类型包括࿱…...

「快学Docker」监控和日志记录容器的健康和性能
「快学Docker」监控和日志记录容器的健康和性能 1. 容器健康状态监控2. 性能监控3. 日志记录几种采集架构图 4. 监控工具和平台cAdvisor(Container Advisor)PrometheusGrafana 5. 自动化运维 1. 容器健康状态监控 方法1:需要实时监测容器的运…...

midjourney过时了?如何使用基于LCM的绘图技术画出你心中的画卷。
生成 AI 艺术在近年来迅速发展,吸引了数百万用户。然而,传统的生成 AI 艺术需要等待几秒钟或几分钟才能生成,这对于快节奏的现代社会来说并不理想。 近日,中国清华大学和 AI 代码共享平台 HuggingFace 联合开发了一项新的机器学习…...

【代码随想录】算法训练计划28
回溯 1、子集 题目: 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 输入:nums [1,2,3] 输出:[[],[1],[2…...

量化交易:筹码理论的探索-筹码分布计算的实现
前言 很多朋友习惯了同花顺、大智慧等看盘软件,经常问到筹码分布如何计算。 说起来筹码分布的理论在庄股时代堪称是一个划时代产品,虽然历经level2数据、资金流统计、拆单算法与反拆单算法等新型技术的变革,庄股时代也逐渐淡出市场…...

常用Redis的键命令参考
一、DEL DEL key [key …] 删除给定的一个或多个 key 。 不存在的 key 会被忽略。 #删除单个键127.0.0.1:6379> set name zhangsan OK 127.0.0.1:6379> del name (integer) 1# 删除一个不存在的 key, 失败,没有 key 被删除127.0.0.1:6379> E…...

Lombok @With 的纯弊端及如何避免
由于是第一篇写关于 Lombok 的日志,所以有些不情愿去开门见山直接触及 With, 而要先提一提本人对 Lombok 的接触过程。 两三年之前写 Java 代码一直都是全手工打造。一个数据类,所有必须的 setter/getter, toString, hashcode() 等全体现在源代码中&…...
无重复字符的最长字串)
C语言每日一题(38)无重复字符的最长字串
力扣 3 无重复字符的最长字串 题目描述 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s…...
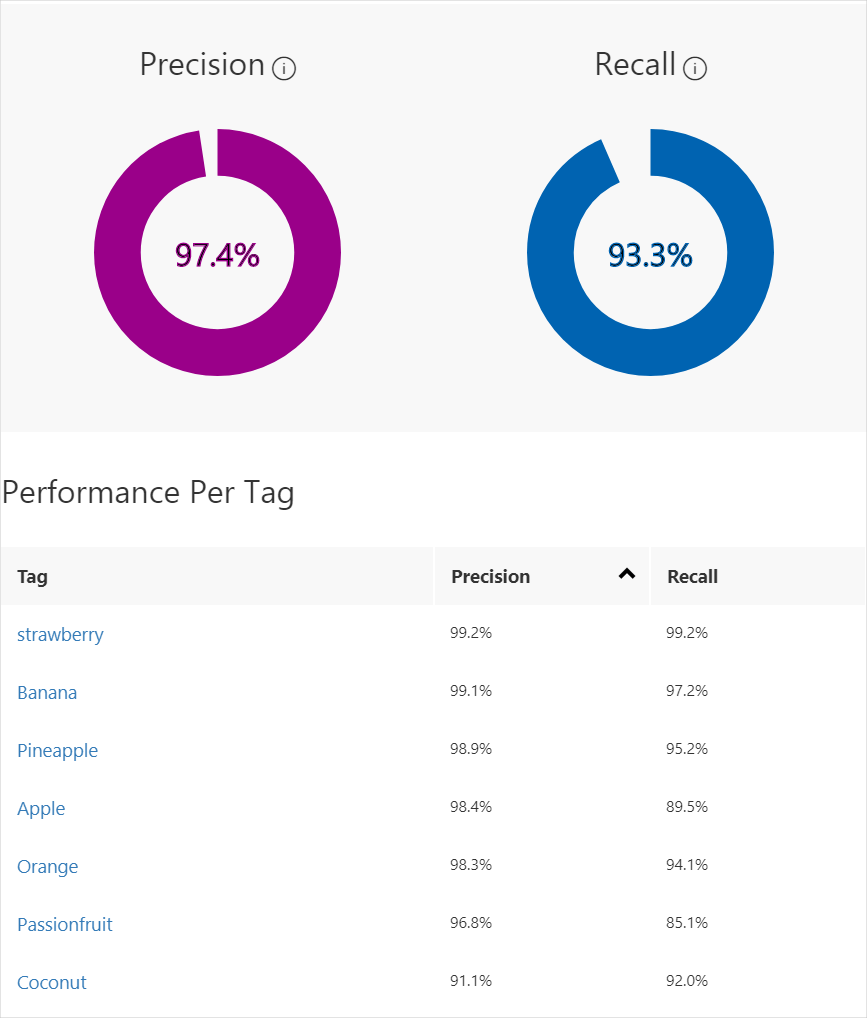
Azure Machine Learning - Azure可视化图像分类操作实战
目录 一、数据准备二、创建自定义视觉资源三、创建新项目四、选择训练图像五、上传和标记图像六、训练分类器七、评估分类器概率阈值 八、管理训练迭代 在本文中,你将了解如何使用Azure可视化页面创建图像分类模型。 生成模型后,可以使用新图像测试该模型…...

PaddleOCR学习笔记
Paddle 功能特性 PP-OCR系列模型列表 https://github.com/PaddlePaddle/PaddleOCR#%EF%B8%8F-pp-ocr%E7%B3%BB%E5%88%97%E6%A8%A1%E5%9E%8B%E5%88%97%E8%A1%A8%E6%9B%B4%E6%96%B0%E4%B8%AD PP-OCR系列模型列表(V4,2023年8月1日更新) 配置文…...
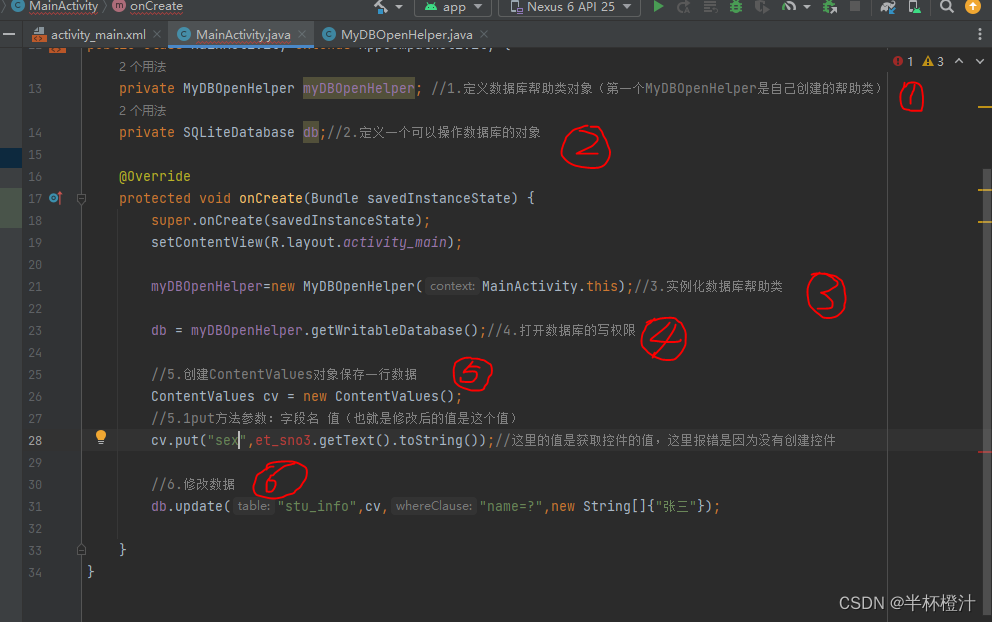
安卓用SQLite数据库存储数据
什么是SQLite? SQLite是安卓中的轻量级内置数据库,不需要设置用户名和密码就可以使用。资源占用较少,运算速度也比较快。 SQLite支持:null(空)、integer(整形)、real(小…...
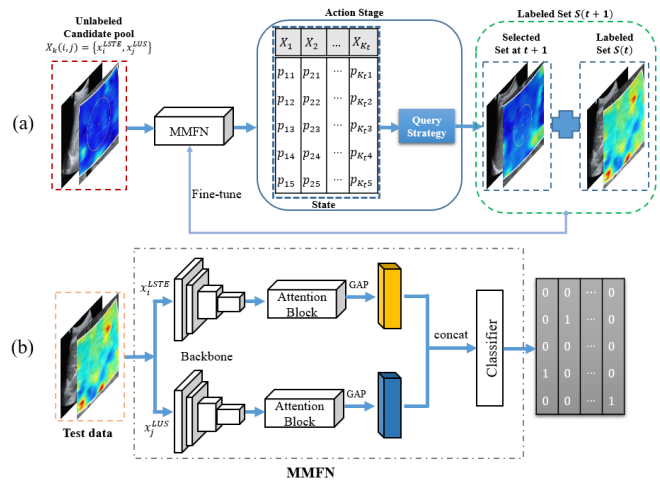
MMFN-AL
MMFN means ‘multi-modal fusion network’ 辅助信息 作者未提供代码...

7、独立按键控制LED状态
按键的抖动 对于机械开关,当机械触点断开、闭合时,由于机械触点的弹性作用,一个开关在闭合时不回马上稳定地接通,在断开时也不会一下子断开,所以在开关闭合及断开的瞬间会伴随一连串的抖动 #include <REGX52.H…...

香蕉派BPI-M4 Zero单板计算机采用全志H618,板载2GRAM内存
Banana Pi BPI-M4 Zero 香蕉派 BPI-M4 Zero是BPI-M2 Zero的最新升级版本。它在性能上有很大的提高。主控芯片升级为全志科技H618 四核A53, CPU主频提升25%。内存升级为2G LPDDR4,板载8G eMMC存储。它支持5G WiFi 和蓝牙, USB接口也升级为type-C。 它具有与树莓派 …...

微信小程序内部跳到外部小程序
要在微信小程序中跳转到外部小程序,可以使用wx.navigateToMiniProgram函数。以下是一个示例: wx.navigateToMiniProgram({appId: 外部小程序的appId,path: 外部小程序的路径,extraData: {id: xxx},success(res) {// 跳转成功} })在这个示例中࿰…...

Spring Boot中设置文件上传大小限制
在Spring Boot中,可以通过以下步骤来设置上传文件的大小: 在application.properties或application.yml文件中,添加以下配置: 对于application.properties: spring.servlet.multipart.max-file-size128MB spring.se…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
