枚举 B. Lorry
Problem - B - Codeforces
题目大意:给物品数量 n n n,体积为 v ( 0 ≤ v ≤ 1 e 9 ) v_{(0 \le v \le 1e9)} v(0≤v≤1e9),第一行读入 n , v n, v n,v,之后 n n n行,读入 n n n个物品,之后每行依次是体积和价值,其中体积要么是1要么是2。要求输出价值和最大,且依次输出所选物品的编号。
思路:发现,体积 v v v很大,用01背包一定不行,01背包优化的事件复杂度是 O ( v ) O(v) O(v),也过不去。但是发现物品的体积要么是1要么是2。我们可以将物品按其体积分为两类,分别表示体积为1的物品和体积为2的物品。之后对于相同体积的物品来说,我们优先考虑其价值最大的那个,所以要对物品进行排序。之后枚举物品体积为1的数量 i i i,得到在物品体积为1的数量 i i i的条件下,得到的最大值,不断的进行更新即可。
代码如下:
void solve() {int n,V; cin>>n>>V;// [0, 0] -> 物品价值,物品编号vector<array<int,2>> t1, t2;t1.push_back({0, 0});t2.push_back({0, 0});for(int i = 0; i < n; ++i) {int v, w; cin>>v>>w;if(v == 1) t1.push_back({w, i + 1});else t2.push_back({w, i + 1});}// 得到物品体积为1的数量,和2的数量int len1 = t1.size() - 1, len2 = t2.size() - 1;// 对物品按照价值从大到小进行排序sort(t1.begin() + 1, t1.end(), [&](auto pre, auto suf) {return pre[0] > suf[0];});sort(t2.begin() + 1, t2.end(), [&](auto pre, auto suf) {return pre[0] > suf[0];});// 得到体积为2的物品的前缀和vector<int> pre(len2 + 1);for(int i = 1; i <= len2; ++i) {pre[i] = pre[i - 1] + t2[i][0];}// 最大值,当前体积为1的物品之和int ma = 0, sum = 0;// 最大值时体积为的个数和体积为2的个数int ans1 = 0, ans2 = 0;// 枚举体积为1的数量,得到最大值for(int i = 0; i <= len1; ++i) {if(i > V) break;int j = min( (V - i) / 2, len2);sum += t1[i][0];if(sum + pre[j] > ma) {ma = sum + pre[j];ans1 = i; ans2 = j;}}// 输出即可cout<<ma<<'\n';for(int i = 1; i <= ans1; ++i) cout<<t1[i][1]<<' ';for(int i = 1; i <= ans2; ++i) cout<<t2[i][1]<<' ';
}
刚开始写的时候,发现定义比较麻烦,就用了map进行映射,发现要处理边界问题,还不如上面简介呢(
void solve() {int n,v; cin>>n>>v;map<int, vector<array<int,2>> > mp;for(int i = 0; i < n; ++i) {int v,w; cin>>v>>w;mp[v].push_back({w, i + 1});}for(int i = 1; i < 3; ++i) {sort(all(mp[i]), [&](auto pre, auto suf) {return pre[0] > suf[0];});}int vlen2 = mp[2].size();vector<int> pre(vlen2 + 1);auto v2(mp[2]);for(int i = 0; i < vlen2; ++i) {pre[i + 1] = pre[i] + v2[i][0];}int sum = 0, ma = 0, need1 = 0, need2 = 0;auto v1(mp[1]);int vlen1 = n - vlen2;ma = pre[min(v / 2, vlen2)]; need2 = min(v / 2, vlen2);for(int i = 1; i <= vlen1; ++i) {if(i > v) break;sum += v1[i-1][0];int j = min( (v - i) / 2, vlen2);if(sum + pre[j] > ma) {ma = sum + pre[j];need1 = i; need2 = j;}}cout<<ma<<'\n';for(int i = 0; i < need1; ++i) {cout<<v1[i][1]<<' ';}for(int i = 0; i < need2; ++i) {cout<<v2[i][1]<<' ';}
}
相关文章:

枚举 B. Lorry
Problem - B - Codeforces 题目大意:给物品数量 n n n,体积为 v ( 0 ≤ v ≤ 1 e 9 ) v_{(0 \le v \le 1e9)} v(0≤v≤1e9),第一行读入 n , v n, v n,v,之后 n n n行,读入 n n n个物品,之后每行依次是体…...
ON1 Photo RAW 2024 for Mac——专业照片编辑的终极利器
ON1 Photo RAW 2024 for Mac是一款专为Mac用户打造的照片编辑器,以其强大的功能和易用的操作,让你的照片编辑工作变得轻松愉快。 一、强大的RAW处理能力 ON1 Photo RAW 2024支持大量的RAW格式照片,能够让你在编辑过程中获得更多的自由度和更…...

从word复制内容到wangEditor富文本框的时候会把html标签也复制过来,如果只想实现直接复制纯文本,有什么好的实现方式
从word复制内容到wangEditor富文本框的时候会把html标签也复制过来,如果只想实现直接复制纯文本,有什么好的实现方式? 将 Word 中的内容复制到富文本编辑器时,常常会带有大量的 HTML 标签和样式,这可能导致不必要的格式…...
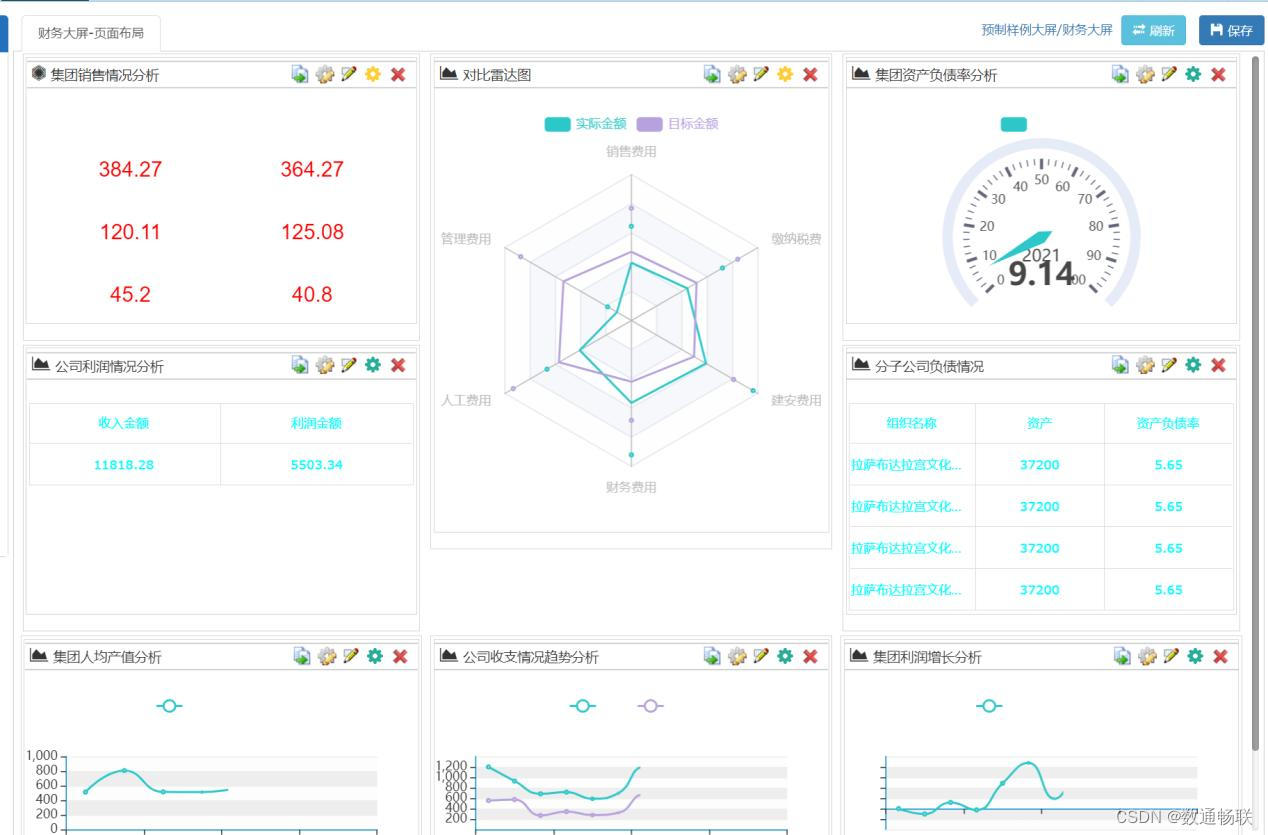
项目中如何配置数据可视化展现
在现今数据驱动的时代,可视化已逐渐成为数据分析的主要途径,可视化大屏的广泛使用便应运而生。很多公司及政务机构,常利用大屏的手段展现其实力或演示业务,可视化的效果能让观者更快速的理解结果并直观的看到数据展现。因此&#…...

ArkUI开发进阶—@Builder函数@BuilderParam装饰器的妙用与场景应用
ArkUI开发进阶—@Builder函数@BuilderParam装饰器的妙用与场景应用 HarmonyOS,作为一款全场景分布式操作系统,为了推动更广泛的应用开发,采用了一种先进而灵活的编程语言——ArkTS。ArkTS是在TypeScript(TS)的基础上发展而来,为HarmonyOS提供了丰富的应用开发工具,使开…...
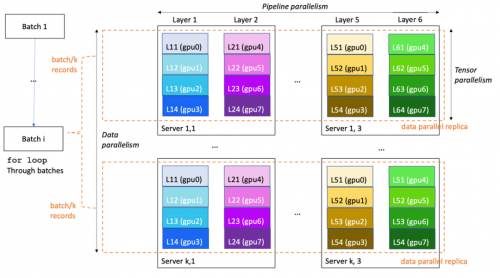
大语言模型概述(三):基于亚马逊云科技的研究分析与实践
上期介绍了基于亚马逊云科技的大语言模型相关研究方向,以及大语言模型的训练和构建优化。本期将介绍大语言模型训练在亚马逊云科技上的最佳实践。 大语言模型训练在亚马逊云科技上的最佳实践 本章节内容,将重点关注大语言模型在亚马逊云科技上的最佳训…...

键入网址到网页显示,期间发生了什么?
文章目录 键入网址到网页显示,期间发生了什么?1. HTTP2. 真实地址查询 —— DNS3. 指南好帮手 —— 协议栈4. 可靠传输 —— TCP5. 远程定位 —— IP6. 两点传输 —— MAC7. 出口 —— 网卡8. 送别者 —— 交换机9. 出境大门 —— 路由器10. 互相扒皮 —…...
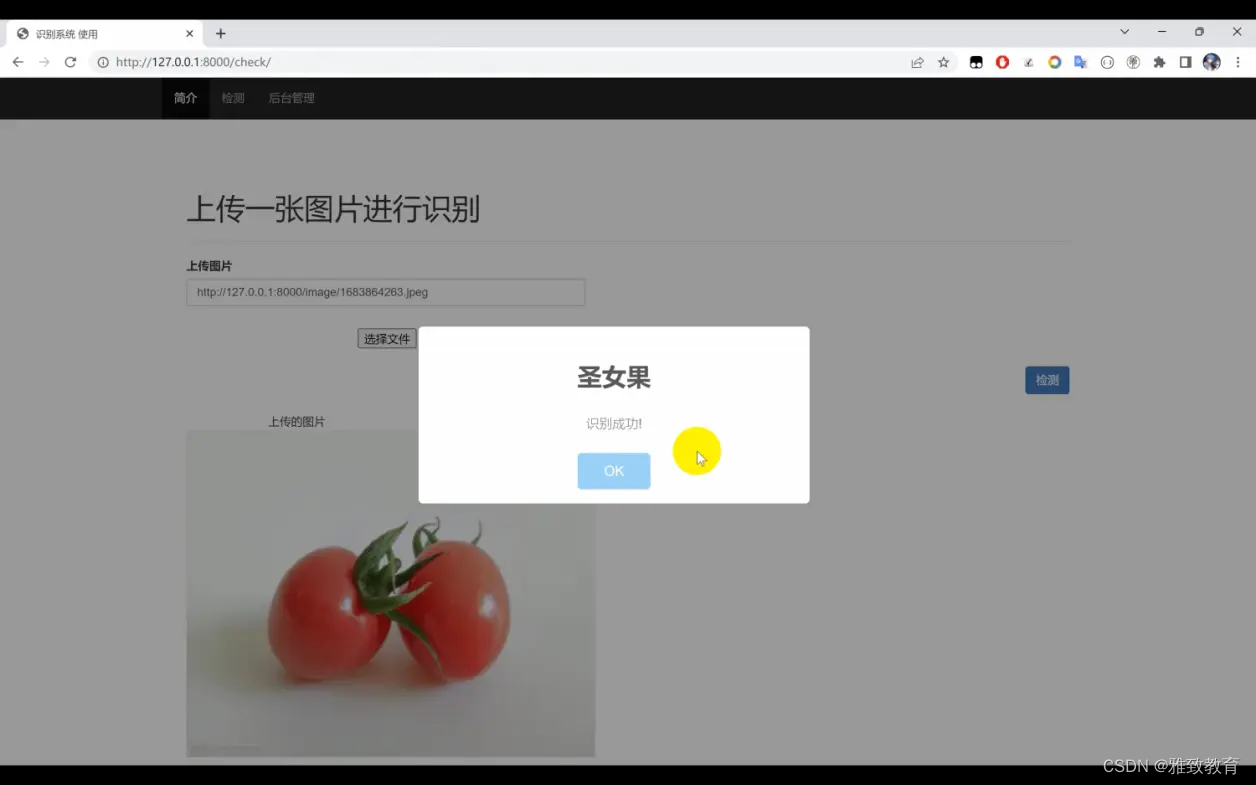
深度学习基于Python+TensorFlow+Django的水果识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介简介技术组合系统功能使用流程 二、功能三、系统四. 总结 一项目简介 # 深度学习基于PythonTensorFlowDjango的水果识别系统介绍 简介 该水果识别系统基于…...

vs动态库生成过程中还存在静态库
为什么VS生成动态库dll同时还会生成lib静态库 动态库与静态库(Windows环境下) 动态库和静态库都是一种可执行代码的二进制形式,可以被操作系统载入内存执行。 静态库实际上是在链接时被链接到exe的,编译后,静态…...
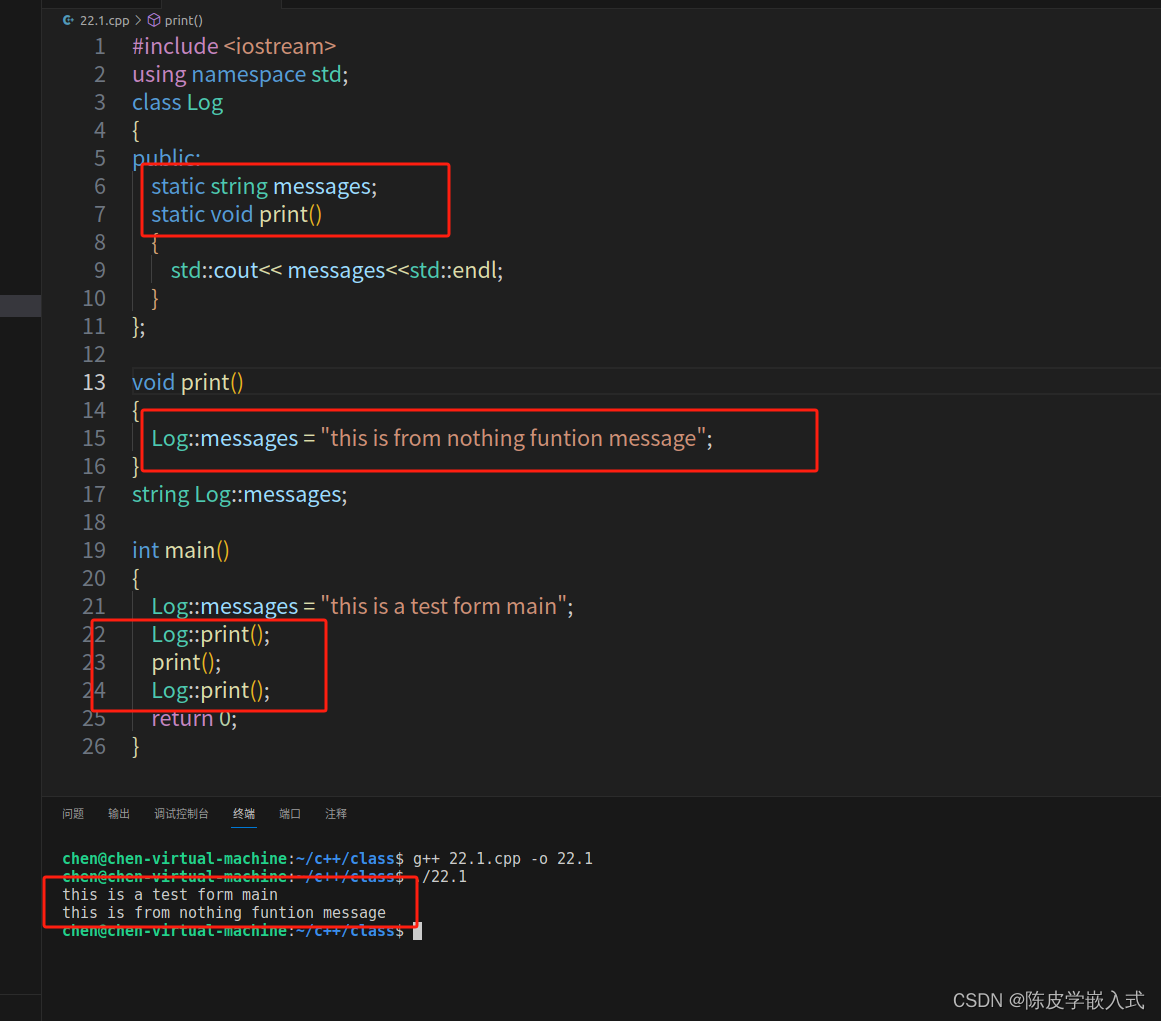
P13 C++ 类 | 结构体内部的静态static
目录 01 前言 02 类内部创建静态变量的例子 03 在类的内部创建静态变量的作用 04 最后的话 01 前言 本期我们讨论 static 在一个类或一个结构体中的具体情况。 在几乎所有面向对象的语言中,静态在一个类中意味着特定的东西。这意味着在类的所有实例中ÿ…...
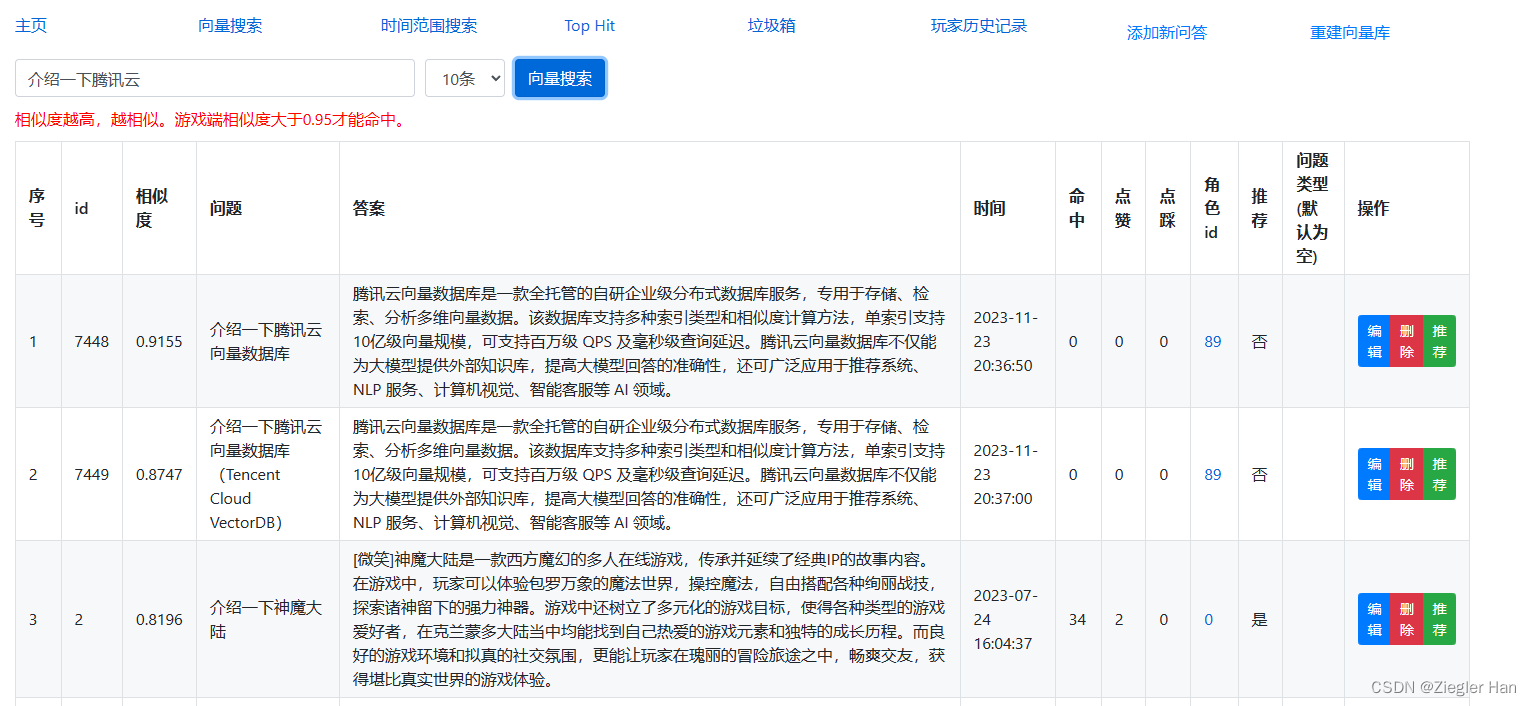
【腾讯云云上实验室-向量数据库】Tencent Cloud VectorDB在实战项目中替换Milvus测试
为什么尝试使用Tencent Cloud VectorDB替换Milvus向量库? 亮点:Tencent Cloud VectorDB支持Embedding,免去自己搭建模型的负担(搭建一个生产环境的模型实在耗费精力和体力)。 腾讯云向量数据库是什么? 腾…...
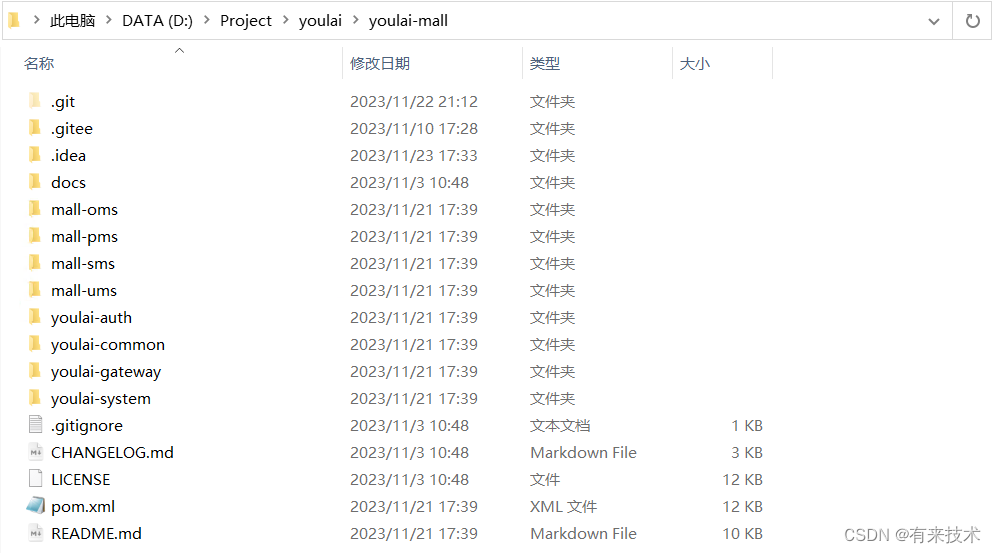
git clone -mirror 和 git clone 的区别
目录 前言两则区别git clone --mirrorgit clone 获取到的文件有什么不同瘦身仓库如何选择结语开源项目 前言 Git是一款强大的版本控制系统,通过Git可以方便地管理代码的版本和协作开发。在使用Git时,常见的操作之一就是通过git clone命令将远程仓库克隆…...

基于51单片机的公交自动报站系统
**单片机设计介绍, 基于51单片机的公交自动报站系统 文章目录 一 概要公交自动报站系统概述工作原理应用与优势 二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 很高兴为您介绍基于51单片机的公交自动报站系统: 公交自动报…...

NextJS开发:Image组件的使用及缺陷
Next.js 中的 Image 组件相比于传统的 img 标签有以下几个优点: 懒加载:Image 组件自带懒加载,当页面滚动到 Image 组件所在位置时才会加载图片,从而加快页面的渲染速度。自动优化:Image 组件会自动将图片压缩、转换格…...

网络安全面试经历
2023-11-22 X亭安全服务实习生面试 一面: 工作方向:偏蓝队 总结:实习蓝队面试没有什么难度,没有什么技术上的细节问题,之前准备的细节问题没有考 最后和面试官聊了聊对网安的认识,聊了聊二进制的知识…...
 - 数据类型)
Rust语言入门教程(四) - 数据类型
标量类型(Scalar Types) 在Rust中,一共有4中标量类型, 也就是基本数据类型,分别是: 整型(Integers)浮点型(Floats)布尔型(Boolean)字符型(Chara…...
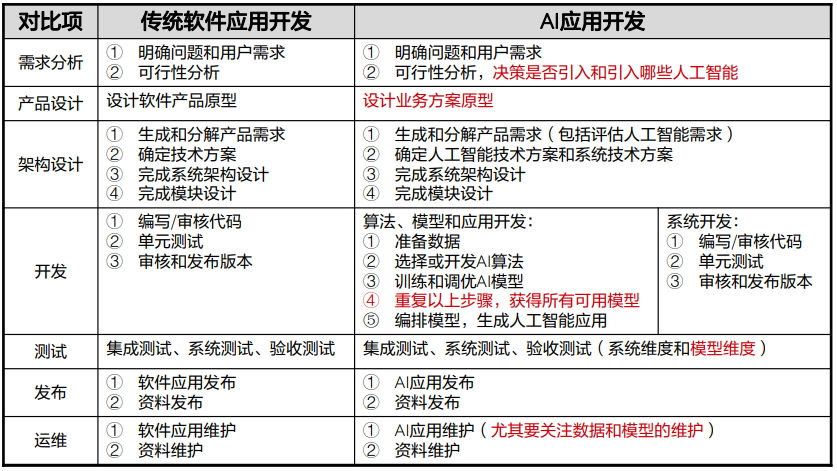
华为云人工智能入门级开发者认证学习笔记
人工智能入门级开发者认证 人工智能定义 定义 人工智能 (Artificial Intelligence) 是研究、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。 强人工智能 vs 弱人工智能 强人工智能:强人工智能观点认为有可能制造出真正能推理(…...

腾讯云发布新一代基于AMD处理器的星星海云服务器实例SA5
基础设施的硬实力,愈发成为云厂商的核心竞争力。 11月24日,腾讯云发布了全新一代星星海服务器。基于自研服务器的高密设计与硬件升级,对应云服务器SA5是全球首家搭载第四代AMD EPYC处理器(Bergamo)的公有云实例&#…...

算法通关村-----数论问题解析
最大公约数和最小公倍数 概念描述 最大公约数(GCD)是指两个或多个整数共有约数中的最大值。 最小公倍数(LCM)是指两个或多个整数共有的倍数中的最小值 方法介绍 碾转相除法 一种用于计算两个整数的最大公约数(GCD…...

wpf prism当中 发布订阅 IEventAggregator
先订阅后发布 private readonly IEventAggregator _eventAggregator; public LoginViewModel(ILoginService iloginService, IEventAggregator eventAggregator) {_iloginService iloginService;_eventAggregator eventAggregator;_eventAggregator.GetEvent<MessageEven…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
