贪心 D. Least Cost Bracket Sequence
Problem - D - Codeforces
题目大意:给一个只包含(,),?三个字符的字符串。每个?可以转为(或者),对于第 i i i个?转为(需要花费 a i a_i ai,转为)需要花费 b i b_i bi。现在问能否让该字符串转为合法的括号匹配,如果可以找到最小花费并输出转为的括号匹配。
思路:?的情况可以转为(,也可以转为),是动态的,处理起来麻烦。我们可以将?全都先转为同一种,记录总花销,之后根据情况替换为另一个,这样虽然也是动态的,但是要维护的状态少了很多。
在此,将?先全部转为),对于中间态而言,左边(可以多,但是)数量一定小于等于左边。用括号匹配的类似操作进行计数,(进行累加计数,对于其他的,如果是?先贪心的转为),之后让计数减一。根据计数值进行贪心的更改:将原来?转)的替换为(,并将计数值和字符串状态进行更新。贪心的时候需要找到中间值 i i i前面的?中 a i − b i a_i - b_i ai−bi最小那个?进行转换。
代码如下:
void solve() {string s; cin>>s;priority_queue<PII> heap;int n = s.size();vector<array<int,2>> a(n); // (val, )valint ans = 0;// 先得到 ? -> ) 的总花销for(int i = 0; i < n; ++i) {if(s[i] == '?') {cin>>a[i][0]>>a[i][1];ans += a[i][1];}}// 判断括号序列是否合法bool ok = 1;int cnt = 0; // 计数for(int i = 0; i < n; ++i) {if(!ok) break;if(s[i] == '(') cnt++;else {// 如果不是 ( 优先转为 ) ,并计算差值,cnt--;if(s[i] == '?') heap.push({a[i][1] - a[i][0], i}), s[i] = ')';// 如果是计数是负数// 将前面的 ( ? -> ) ) -> ( 转为 (// 并更新计数和字符串值if(cnt < 0) {if(heap.size() == 0) ok = 0;else {auto tmp = heap.top(); heap.pop();ans -= tmp.first;cnt += 2;s[tmp.second] = '(';}}}}if(cnt || !ok) puts("-1");else {cout<<ans<<'\n';cout<<s<<'\n';}
}
相关文章:

贪心 D. Least Cost Bracket Sequence
Problem - D - Codeforces 题目大意:给一个只包含(,),?三个字符的字符串。每个?可以转为(或者),对于第 i i i个?转为(需要花费 a i a_i ai,转为)需要花费 b i b_i bi。现在问能否让该字符串转为合法的括号匹配…...
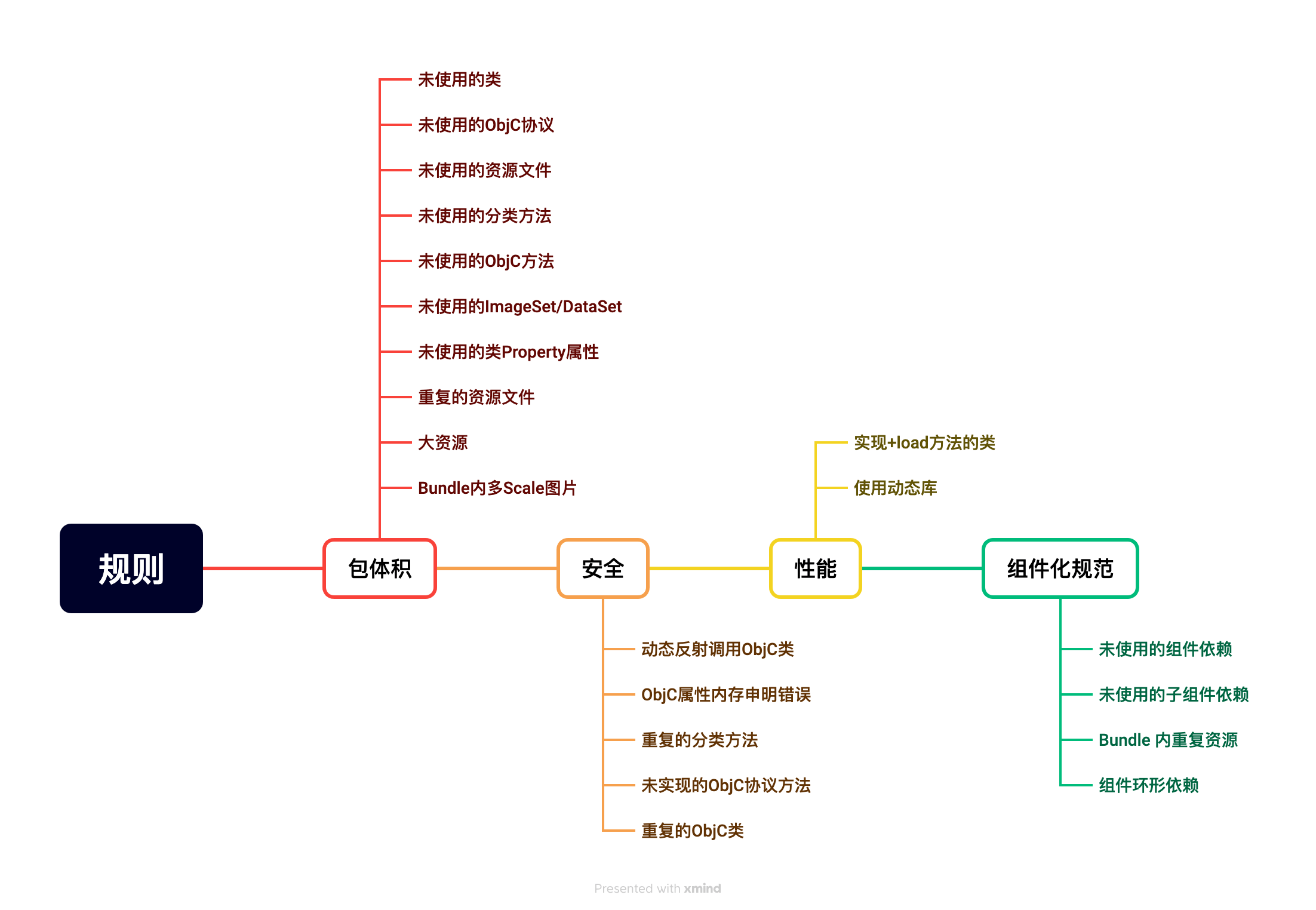
iOS APP包分析工具 | 京东云技术团队
介绍 分享一款用于分析iOSipa包的脚本工具,使用此工具可以自动扫描发现可修复的包体积问题,同时可以生成包体积数据用于查看。这块工具我们团队内部已经使用很长一段时间,希望可以帮助到更多的开发同学更加效率的优化包体积问题。 工具下载…...
在 VSCode 中使用 GDB 进行 C/C++ 程序调试(图文版)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...

任意文件读取漏洞理解
任意文件读取漏洞理解 1. 漏洞描述: 任意文件读取漏洞是指攻击者可以利用漏洞读取系统上的任意文件,包括敏感信息的配置文件、用户数据甚至系统文件,从而获取未经授权的访问权限。 2. 漏洞原理: 这种漏洞通常是由程序处理用户输入…...

linux 安装yum
问题1:File "/usr/libexec/urlgrabber-ext-down", line 28 except OSError, e: ^ 问题2:yum File "/usr/bin/yum", line 30 except KeyboardInterrupt, e: ^ vim /usr/…...

数学启发式
学习资料: 优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现 数学启发式算法 | 可行性泵 (Feasibility Pump)算法精讲:一份让您满意的【理论介绍编程实现数值实验】学习笔记(PythonGurobi实现) 大佬到底是大佬!这些资料太…...

Win10/Win11 使用Wsl的Ubuntu 子系统搭建CGO环境,相当于Ubuntu下开发。GO环境CGO搭建,支持交叉编译
背景: 之前是使用Mac 开发,最近切换到win11下面。发现使用cgo编译有问题。 下面记载了我的使用方法。 环境: win11(win10理论一样) win11 安装了wsl2的环境,并且安装了ubuntu系统。 在win11 上面安装了g…...

CSS新特性(2-2)
CSS新特性(2-2) 前言box相关box-shadow background背景rgba颜色与透明度transform:rotate(Xdeg) 2D旋转transform:tranlate 平移 前言 本文继续讲解CSS3其他的新特性,想看之前新特性点击这里,那么好本文正式开始。 box相关 box…...
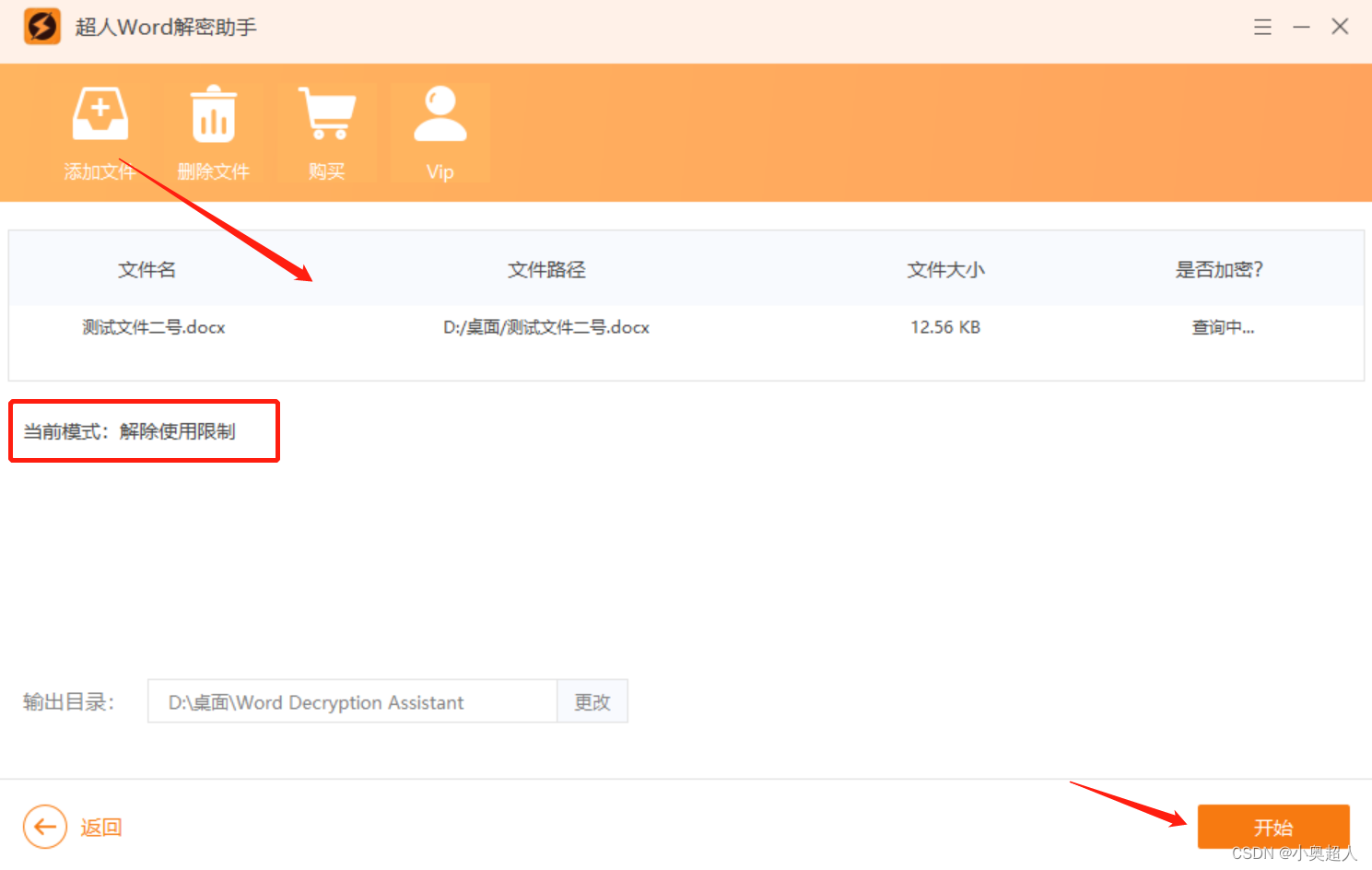
为什么,word文件在只读模式下,仍然能编辑?
Word文档设置了只读模式,是可以编辑的,但是当我们进行保存的时候就会发现,word提示需要重命名并选择新路径才能够保存。 这种操作,即使可以编辑文字,但是原文件是不会受到影响的,编辑之后的word文件会保存到…...

29 - 装饰器模式:如何优化电商系统中复杂的商品价格策略?
开始今天的学习之前,我想先请你思考一个问题。假设现在有这样一个需求,让你设计一个装修功能,用户可以动态选择不同的装修功能来装饰自己的房子。例如,水电装修、天花板以及粉刷墙等属于基本功能,而设计窗帘装饰窗户、…...
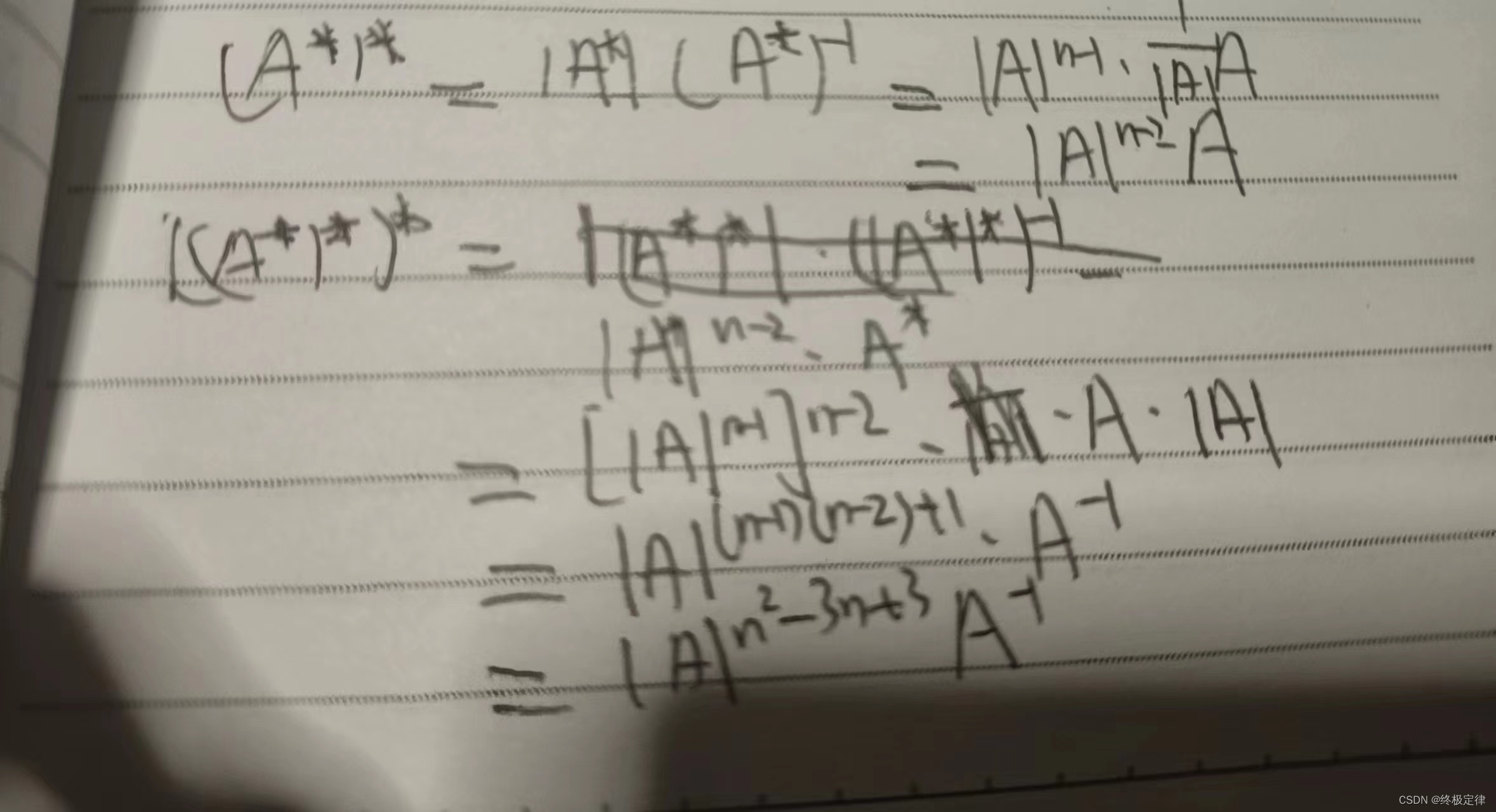
逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。 1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等) 2.性质二:|ka||a|*k的n次方,n为方阵阶数。 …...

Ruoyi项目传List到后台并使用Excel模板下载数据的方法以及遇到的各种前后端数据交互问题
import { download } from @/utils/requestconst app = createApp(App)// 全局方法挂载 app.config.globalProperties.download = download 首先因为ruoyi-ui中的main.js有配置如上全局注册: 因此只需要在vue中定义一个方法直接使用this.download调用下载即可: (download的3…...

区块链技术将如何影响未来的数字营销?
你是否听腻了区块链和数字营销等流行语,却不明白它们对未来意味着什么?那么,准备好系好安全带吧,因为区块链技术将彻底改变我们对数字营销的看法。从建立消费者信任到提高透明度和效率,其可能性是无限的。 让我们来探…...

小程序wx:if和hidden的区别?
wx:if:wx:if 是一个完整的条件渲染指令,当它的表达式为真时,才会渲染该指令所在的元素。如果表达式的值为假,则不会渲染该元素。这意味着在表达式为假时,该元素及其子元素都不会被渲染,就像它们从未存在过一…...

分布式幂等
分布式幂等 在分布式系统、网络通信和数据库操作中,幂等性是一个非常重要的概念,特别是在面对可能发生网络故障、消息重复、或者系统崩溃等情况时。 举个简单的例子,考虑一个银行转账的操作。如果转账操作是幂等的,那么无论你执…...

大数据 DataX-Web 详细安装教程
目录 一、DataX-Web 介绍 1.1 DataX-Web 是什么 1.2 DataX-Web 架构 二、DataX-Web 安装部署 2.1 环境要求 2.2 安装 2.3 部署 2.4 数据库初始化 2.5 配置 2.6 启动服务 2.6.1 一键启动所有服务 2.6.2 一键取消所有服务 2.7 查看服务(注意!…...

CSS3媒体查询实现不同宽度的下不同内容的展示
文章目录 前言CSS3 多媒体查询实例520 到 699px 宽度 - 添加邮箱图标700 到 1000px - 添加文本前缀信息大于 1001px 宽度 - 添加邮件地址大于 1151px 宽度 - 添加图标代码后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:CSS ὃ…...

使用 STM32 读取和解析 NTC 热敏电阻的数值
本文介绍了如何利用 STM32 微控制器读取和解析 NTC(Negative Temperature Coefficient)热敏电阻的数值。首先,我们将简要介绍 NTC 热敏电阻的原理和特性。接下来,我们将详细讨论如何设计电路连接和采用合适的 STM32 外设进行数值读…...

C#,数值计算——有理函数插值和外推(Rational_interp)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 有理函数插值和外推 /// Rational Function Interpolation and Extrapolation /// Given a value x, and using pointers to data xx and yy, this routine returns …...

力扣283:移动零(JAVA)
题目描述: 意思是将所有0移到最后的同时其余非0元素位置仍然不变 如 1 2 0 5 2 0 经过移动零后变为 1 2 5 2 0 0 思路:使用双指针的思路来写 fast:从左往右遍历数组 slow:非零元素最后的一个位置 将数组分为3个区间 [0,slow]为处理好的非0数据,slow永远指向最后一个非0数据 [s…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
