基于C#实现Kruskal算法
这篇我们看看第二种生成树的 Kruskal 算法,这个算法的魅力在于我们可以打一下算法和数据结构的组合拳,很有意思的。
一、思想
若存在 M={0,1,2,3,4,5}这样 6 个节点,我们知道 Prim 算法构建生成树是从”顶点”这个角度来思考的,然后采用“贪心思想”来一步步扩大化,最后形成整体最优解,而 Kruskal 算法有点意思,它是站在”边“这个角度在思考的,首先我有两个集合。
1.1、顶点集合(vertexs)
比如 M 集合中的每个元素都可以认为是一个独根树(是不是想到了并查集?)。
1.2、边集合(edges)
对图中的每条边按照权值大小进行排序。(是不是想到了优先队列?)
首先:我们从 edges 中选出权值最小的一条边来作为生成树的一条边,然后将该边的两个顶点合并为一个新的树。
然后:我们继续从 edges 中选出次小的边作为生成树的第二条边,但是前提就是边的两个顶点一定是属于两个集合中,如果不是则剔除该边继续选下一条次小边。
最后:经过反复操作,当我们发现 n 个顶点的图中生成树已经有 n-1 边的时候,此时生成树构建完毕。
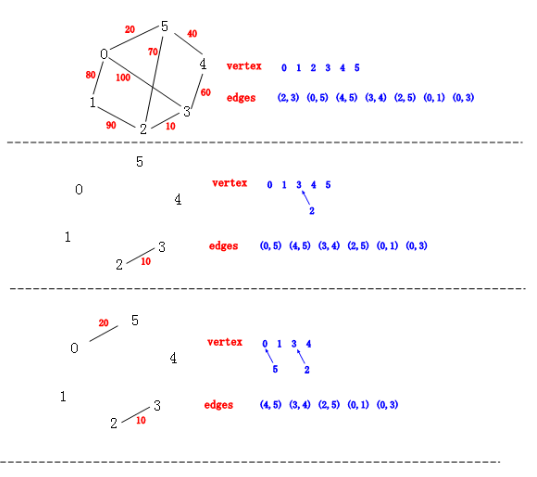
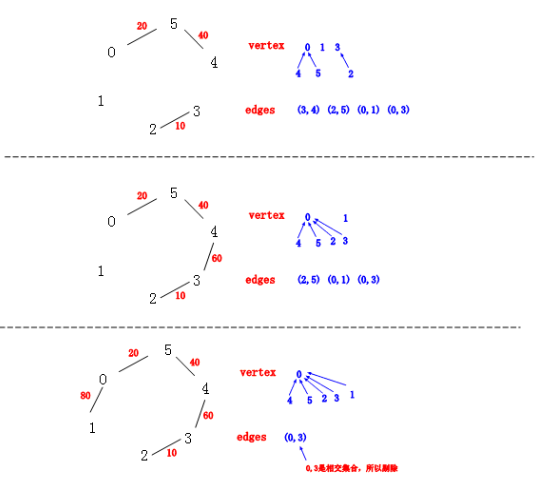
从图中我们还是很清楚的看到 Kruskal 算法构建生成树的详细过程,同时我们也看到了”并查集“和“优先队列“这两个神器来加速我们的生成树构建。
二、构建
2.1、Build 方法
这里我灌的是一些测试数据,同时在矩阵构建完毕后,将顶点信息放入并查集,同时将边的信息放入优先队列,方便我们在做生成树的时候秒杀。
#region 矩阵的构建/// <summary>/// 矩阵的构建/// </summary>public void Build(){//顶点数graph.vertexsNum = 6;//边数graph.edgesNum = 8;graph.vertexs = new int[graph.vertexsNum];graph.edges = new int[graph.vertexsNum, graph.vertexsNum];//构建二维数组for (int i = 0; i < graph.vertexsNum; i++){//顶点graph.vertexs[i] = i;for (int j = 0; j < graph.vertexsNum; j++){graph.edges[i, j] = int.MaxValue;}}graph.edges[0, 1] = graph.edges[1, 0] = 80;graph.edges[0, 3] = graph.edges[3, 0] = 100;graph.edges[0, 5] = graph.edges[5, 0] = 20;graph.edges[1, 2] = graph.edges[2, 1] = 90;graph.edges[2, 5] = graph.edges[5, 2] = 70;graph.edges[4, 5] = graph.edges[5, 4] = 40;graph.edges[3, 4] = graph.edges[4, 3] = 60;graph.edges[2, 3] = graph.edges[3, 2] = 10;//优先队列,存放树中的边queue = new PriorityQueue<Edge>();//并查集set = new DisjointSet<int>(graph.vertexs);//将对角线读入到优先队列for (int i = 0; i < graph.vertexsNum; i++){for (int j = i; j < graph.vertexsNum; j++){//说明该边有权重if (graph.edges[i, j] != int.MaxValue){queue.Eequeue(new Edge(){startEdge = i,endEdge = j,weight = graph.edges[i, j]}, graph.edges[i, j]);}}}}#endregion
2.2、Kruskal 算法
并查集,优先队列都有数据了,下面我们只要出队操作就行了,如果边的顶点不在一个集合中,我们将其收集作为最小生成树的一条边,按着这样的方式,最终生成树构建完毕。
#region Kruskal算法/// <summary>/// Kruskal算法/// </summary>public List<Edge> Kruskal(){//最后收集到的最小生成树的边List<Edge> list = new List<Edge>();//循环队列while (queue.Count() > 0){var edge = queue.Dequeue();//如果该两点是同一个集合,则剔除该集合if (set.IsSameSet(edge.t.startEdge, edge.t.endEdge))continue;list.Add(edge.t);//然后将startEdge 和 endEdge Union起来,表示一个集合set.Union(edge.t.startEdge, edge.t.endEdge);//如果n个节点有n-1边的时候,此时生成树已经构建完毕,提前退出if (list.Count == graph.vertexsNum - 1)break;}return list;}#endregion
最后是总的代码:
using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Diagnostics;using System.Threading;using System.IO;using System.Threading.Tasks;namespace ConsoleApplication2{public class Program{public static void Main(){MatrixGraph graph = new MatrixGraph();graph.Build();var edges = graph.Kruskal();foreach (var edge in edges){Console.WriteLine("({0},{1})({2})", edge.startEdge, edge.endEdge, edge.weight);}Console.Read();}}#region 定义矩阵节点/// <summary>/// 定义矩阵节点/// </summary>public class MatrixGraph{Graph graph = new Graph();PriorityQueue<Edge> queue;DisjointSet<int> set;public class Graph{/// <summary>/// 顶点信息/// </summary>public int[] vertexs;/// <summary>/// 边的条数/// </summary>public int[,] edges;/// <summary>/// 顶点个数/// </summary>public int vertexsNum;/// <summary>/// 边的个数/// </summary>public int edgesNum;}#region 矩阵的构建/// <summary>/// 矩阵的构建/// </summary>public void Build(){//顶点数graph.vertexsNum = 6;//边数graph.edgesNum = 8;graph.vertexs = new int[graph.vertexsNum];graph.edges = new int[graph.vertexsNum, graph.vertexsNum];//构建二维数组for (int i = 0; i < graph.vertexsNum; i++){//顶点graph.vertexs[i] = i;for (int j = 0; j < graph.vertexsNum; j++){graph.edges[i, j] = int.MaxValue;}}graph.edges[0, 1] = graph.edges[1, 0] = 80;graph.edges[0, 3] = graph.edges[3, 0] = 100;graph.edges[0, 5] = graph.edges[5, 0] = 20;graph.edges[1, 2] = graph.edges[2, 1] = 90;graph.edges[2, 5] = graph.edges[5, 2] = 70;graph.edges[4, 5] = graph.edges[5, 4] = 40;graph.edges[3, 4] = graph.edges[4, 3] = 60;graph.edges[2, 3] = graph.edges[3, 2] = 10;//优先队列,存放树中的边queue = new PriorityQueue<Edge>();//并查集set = new DisjointSet<int>(graph.vertexs);//将对角线读入到优先队列for (int i = 0; i < graph.vertexsNum; i++){for (int j = i; j < graph.vertexsNum; j++){//说明该边有权重if (graph.edges[i, j] != int.MaxValue){queue.Eequeue(new Edge(){startEdge = i,endEdge = j,weight = graph.edges[i, j]}, graph.edges[i, j]);}}}}#endregion#region 边的信息/// <summary>/// 边的信息/// </summary>public class Edge{//开始边public int startEdge;//结束边public int endEdge;//权重public int weight;}#endregion#region Kruskal算法/// <summary>/// Kruskal算法/// </summary>public List<Edge> Kruskal(){//最后收集到的最小生成树的边List<Edge> list = new List<Edge>();//循环队列while (queue.Count() > 0){var edge = queue.Dequeue();//如果该两点是同一个集合,则剔除该集合if (set.IsSameSet(edge.t.startEdge, edge.t.endEdge))continue;list.Add(edge.t);//然后将startEdge 和 endEdge Union起来,表示一个集合set.Union(edge.t.startEdge, edge.t.endEdge);//如果n个节点有n-1边的时候,此时生成树已经构建完毕,提前退出if (list.Count == graph.vertexsNum - 1)break;}return list;}#endregion}#endregion}
并查集:
using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication2{/// <summary>/// 并查集/// </summary>public class DisjointSet<T> where T : IComparable{#region 树节点/// <summary>/// 树节点/// </summary>public class Node{/// <summary>/// 父节点/// </summary>public T parent;/// <summary>/// 节点的秩/// </summary>public int rank;}#endregionDictionary<T, Node> dic = new Dictionary<T, Node>();public DisjointSet(T[] c){Init(c);}#region 做单一集合的初始化操作/// <summary>/// 做单一集合的初始化操作/// </summary>public void Init(T[] c){//默认的不想交集合的父节点指向自己for (int i = 0; i < c.Length; i++){dic.Add(c[i], new Node(){parent = c[i],rank = 0});}}#endregion#region 判断两元素是否属于同一个集合/// <summary>/// 判断两元素是否属于同一个集合/// </summary>/// <param name="root1"></param>/// <param name="root2"></param>/// <returns></returns>public bool IsSameSet(T root1, T root2){return Find(root1).CompareTo(Find(root2)) == 0;}#endregion#region 查找x所属的集合/// <summary>/// 查找x所属的集合/// </summary>/// <param name="x"></param>/// <returns></returns>public T Find(T x){//如果相等,则说明已经到根节点了,返回根节点元素if (dic[x].parent.CompareTo(x) == 0)return x;//路径压缩(回溯的时候赋值,最终的值就是上面返回的"x",也就是一条路径上全部被修改了)return dic[x].parent = Find(dic[x].parent);}#endregion#region 合并两个不相交集合/// <summary>/// 合并两个不相交集合/// </summary>/// <param name="root1"></param>/// <param name="root2"></param>/// <returns></returns>public void Union(T root1, T root2){T x1 = Find(root1);T y1 = Find(root2);//如果根节点相同则说明是同一个集合if (x1.CompareTo(y1) == 0)return;//说明左集合的深度 < 右集合if (dic[x1].rank < dic[y1].rank){//将左集合指向右集合dic[x1].parent = y1;}else{//如果 秩 相等,则将 y1 并入到 x1 中,并将x1++if (dic[x1].rank == dic[y1].rank)dic[x1].rank++;dic[y1].parent = x1;}}#endregion}}
优先队列:
using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Diagnostics;using System.Threading;using System.IO;namespace ConsoleApplication2{public class PriorityQueue<T> where T : class{/// <summary>/// 定义一个数组来存放节点/// </summary>private List<HeapNode> nodeList = new List<HeapNode>();#region 堆节点定义/// <summary>/// 堆节点定义/// </summary>public class HeapNode{/// <summary>/// 实体数据/// </summary>public T t { get; set; }/// <summary>/// 优先级别 1-10个级别 (优先级别递增)/// </summary>public int level { get; set; }public HeapNode(T t, int level){this.t = t;this.level = level;}public HeapNode() { }}#endregion#region 添加操作/// <summary>/// 添加操作/// </summary>public void Eequeue(T t, int level = 1){//将当前节点追加到堆尾nodeList.Add(new HeapNode(t, level));//如果只有一个节点,则不需要进行筛操作if (nodeList.Count == 1)return;//获取最后一个非叶子节点int parent = nodeList.Count / 2 - 1;//堆调整UpHeapAdjust(nodeList, parent);}#endregion#region 对堆进行上滤操作,使得满足堆性质/// <summary>/// 对堆进行上滤操作,使得满足堆性质/// </summary>/// <param name="nodeList"></param>/// <param name="index">非叶子节点的之后指针(这里要注意:我们/// 的筛操作时针对非叶节点的)/// </param>public void UpHeapAdjust(List<HeapNode> nodeList, int parent){while (parent >= 0){//当前index节点的左孩子var left = 2 * parent + 1;//当前index节点的右孩子var right = left + 1;//parent子节点中最大的孩子节点,方便于parent进行比较//默认为left节点var min = left;//判断当前节点是否有右孩子if (right < nodeList.Count){//判断parent要比较的最大子节点min = nodeList[left].level < nodeList[right].level ? left : right;}//如果parent节点大于它的某个子节点的话,此时筛操作if (nodeList[parent].level > nodeList[min].level){//子节点和父节点进行交换操作var temp = nodeList[parent];nodeList[parent] = nodeList[min];nodeList[min] = temp;//继续进行更上一层的过滤parent = (int)Math.Ceiling(parent / 2d) - 1;}else{break;}}}#endregion#region 优先队列的出队操作/// <summary>/// 优先队列的出队操作/// </summary>/// <returns></returns>public HeapNode Dequeue(){if (nodeList.Count == 0)return null;//出队列操作,弹出数据头元素var pop = nodeList[0];//用尾元素填充头元素nodeList[0] = nodeList[nodeList.Count - 1];//删除尾节点nodeList.RemoveAt(nodeList.Count - 1);//然后从根节点下滤堆DownHeapAdjust(nodeList, 0);return pop;}#endregion#region 对堆进行下滤操作,使得满足堆性质/// <summary>/// 对堆进行下滤操作,使得满足堆性质/// </summary>/// <param name="nodeList"></param>/// <param name="index">非叶子节点的之后指针(这里要注意:我们/// 的筛操作时针对非叶节点的)/// </param>public void DownHeapAdjust(List<HeapNode> nodeList, int parent){while (2 * parent + 1 < nodeList.Count){//当前index节点的左孩子var left = 2 * parent + 1;//当前index节点的右孩子var right = left + 1;//parent子节点中最大的孩子节点,方便于parent进行比较//默认为left节点var min = left;//判断当前节点是否有右孩子if (right < nodeList.Count){//判断parent要比较的最大子节点min = nodeList[left].level < nodeList[right].level ? left : right;}//如果parent节点小于它的某个子节点的话,此时筛操作if (nodeList[parent].level > nodeList[min].level){//子节点和父节点进行交换操作var temp = nodeList[parent];nodeList[parent] = nodeList[min];nodeList[min] = temp;//继续进行更下一层的过滤parent = min;}else{break;}}}#endregion#region 获取元素并下降到指定的level级别/// <summary>/// 获取元素并下降到指定的level级别/// </summary>/// <returns></returns>public HeapNode GetAndDownPriority(int level){if (nodeList.Count == 0)return null;//获取头元素var pop = nodeList[0];//设置指定优先级(如果为 MinValue 则为 -- 操作)nodeList[0].level = level == int.MinValue ? --nodeList[0].level : level;//下滤堆DownHeapAdjust(nodeList, 0);return nodeList[0];}#endregion#region 获取元素并下降优先级/// <summary>/// 获取元素并下降优先级/// </summary>/// <returns></returns>public HeapNode GetAndDownPriority(){//下降一个优先级return GetAndDownPriority(int.MinValue);}#endregion#region 返回当前优先队列中的元素个数/// <summary>/// 返回当前优先队列中的元素个数/// </summary>/// <returns></returns>public int Count(){return nodeList.Count;}#endregion}}
相关文章:

基于C#实现Kruskal算法
这篇我们看看第二种生成树的 Kruskal 算法,这个算法的魅力在于我们可以打一下算法和数据结构的组合拳,很有意思的。 一、思想 若存在 M{0,1,2,3,4,5}这样 6 个节点,我们知道 Prim 算法构建生成树是从”顶点”这个角度来思考的,然…...
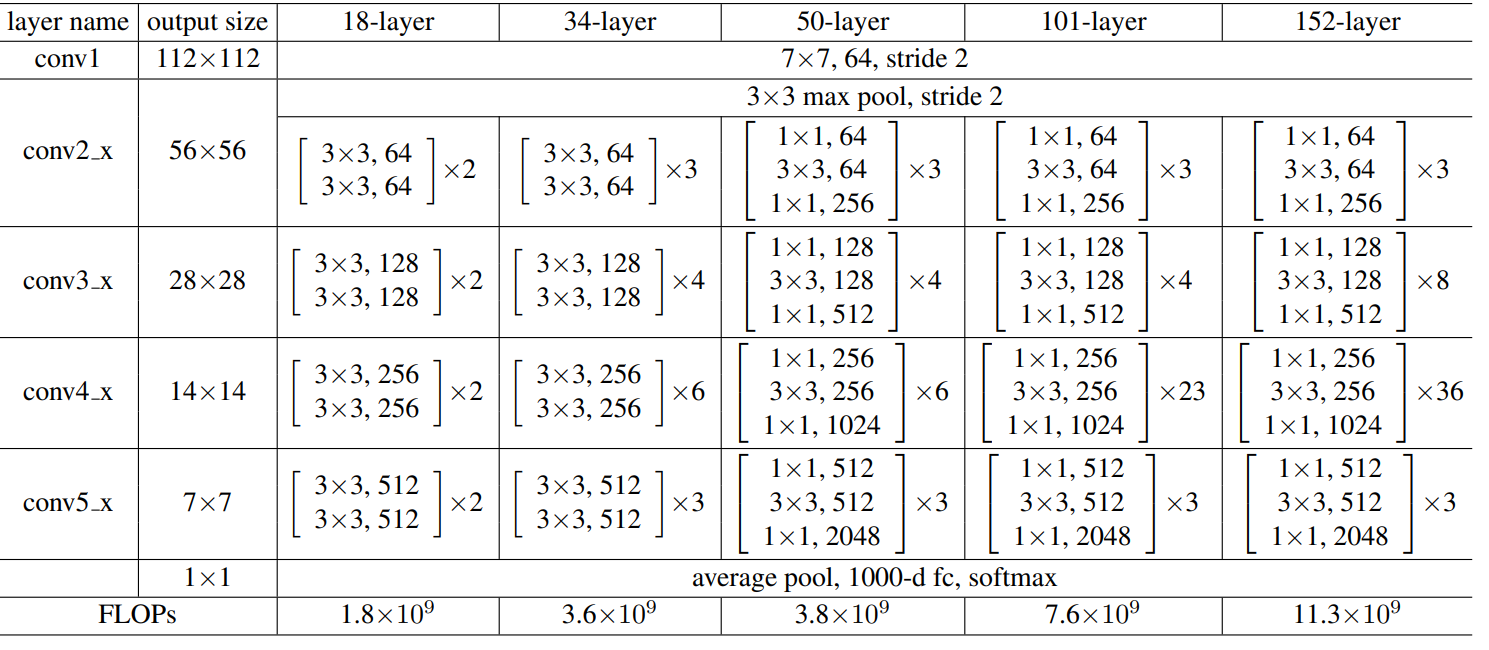
卷积神经网络经典backbone
特征提取是数据分析和机器学习中的基本概念,是将原始数据转换为更适合分析或建模的格式过程中的关键步骤。特征,也称为变量或属性,是我们用来进行预测、对对象进行分类或从数据中获取见解的数据点的特定特征或属性。 1.AlexNet paper&#…...

【2023 年终盘点】今年用的最多的 10 款浏览器插件
分享顺哥今年用的最多的 10 款浏览器插件。 排名不分先后,涉及各个方面的应用。 大家有好用的插件也欢迎在评论区留言分享! 视频 YouTube:https://youtu.be/ZpTydUSBwCA 顺哥博客 浏览器扩展篇 注意: 1、以下介绍的均为在 Google Chrome 浏览器适用的小插件,部分插件…...

GWAS:plink进行meta分析
之前教程提到过Metal是可以做Meta分析,除了Metal,PLINK也可以进行Meta分析。 命令如下所示: plink --meta-analysis gwas1.plink gwas2.plink gwas3.plink logscale qt --meta-analysis-snp-field SNP --meta-analysis-chr-field CHR --me…...
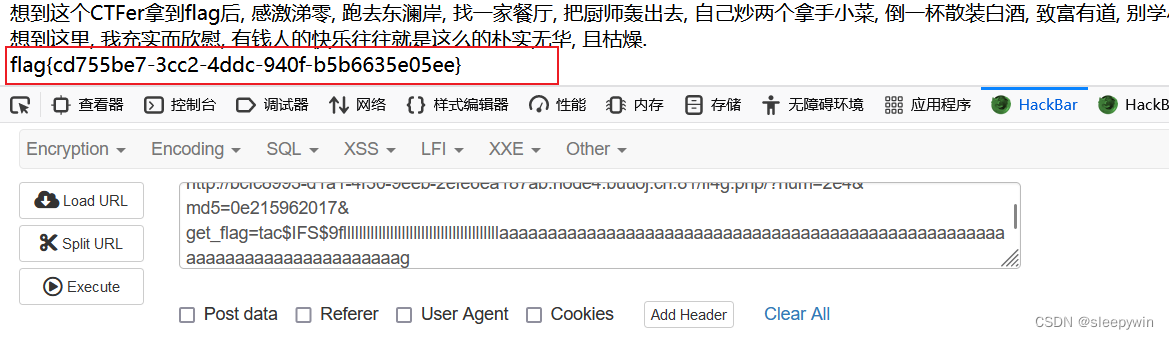
web:[WUSTCTF2020]朴实无华
题目 点开页面显示如下 页面显示了一行报错:Cannot modify header information - headers already sent by (output started at /var/www/html/index.php:3) in /var/www/html/index.php on line 4 意思为不能修改报头信息-报头已经发送(输出开始于/var/www/html/i…...
)
云原生安全工具汇总(docker、k8s、Kubernetes、Git仓库)
目录 Metarget:云原生靶机环境 CDK:容器环境定制的渗透测试工具 container-escape-check:容器逃逸检测...

基于51单片机超声波测距汽车避障系统
**单片机设计介绍, 基于51单片机超声波测距汽车避障系统 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于51单片机的超声波测距汽车避障系统是一种用于帮助汽车避免碰撞和发生事故的设备,以下是一个基本…...
git的使用:本地git下载、sshkey的添加、github仓库创建及文件上传
一、github创建账号 即github注册账号,登录github官网,根据提示注册即可 github官网 二、git客户端下载安装 已有很多git下载安装的博文了,在此就不赘述 三、sshkey的生成与添加 1、sshkey的生成以及查看 // sshkey的生成命令ÿ…...

增量有余、后劲不足,星途汽车10月份销量环比下降3.9%
撰稿|行星 来源|贝多财经 近日,奇瑞集团发布了10月销量月报。报告显示,奇瑞集团于2023年10月销售汽车20.03万辆,同比增长50.8%,单月销量首次突破20万辆;2023年前10个月的累计销量为145.36辆,同比增长41.6…...
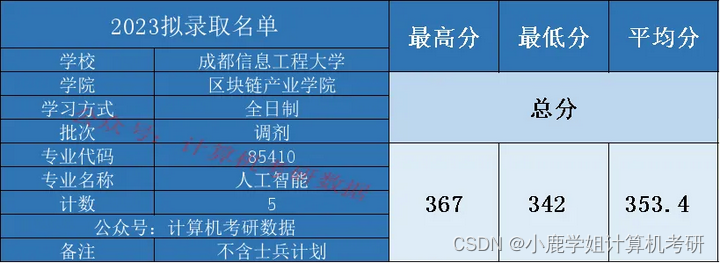
只考数据结构,计算机评级C+,成都信息工程大学考情分析
成都信息工程大学(C) 考研难度(☆☆) 内容:23考情概况(拟录取和复试分析)、院校概况、24专业目录、23复试详情、各专业考情分析、各科目考情分析。 正文1715字,预计阅读:3分钟 2023考情概况 …...

Screen操作
detach:detach是指将当前运行的Screen会话从终端分离(detach),使其在后台继续运行而不受当前终端窗口的影响。这样,你可以在一个终端窗口中启动一个Screen会话,然后在需要的时候将其分离,使其在…...

js基础知识
1. beforeCreate 初始化界面前 : 在当前阶段data、methods、computed以及watch上的数据和方法都不能被访问。 2. created 初始化界面后 : 在实例创建完成后发生,当前阶段已经完成了数据观测,也就是可以使用数据,更改数据,在这里更…...
Vue常见的实现tab切换的两种方法
目录 方法一:事件绑定属性绑定 效果图 完整代码 方法二:属性绑定 动态组件 component标签 效果图 完整代码 方法一:事件绑定属性绑定 效果图 完整代码 <!DOCTYPE html> <html lang"en"> <head><meta c…...
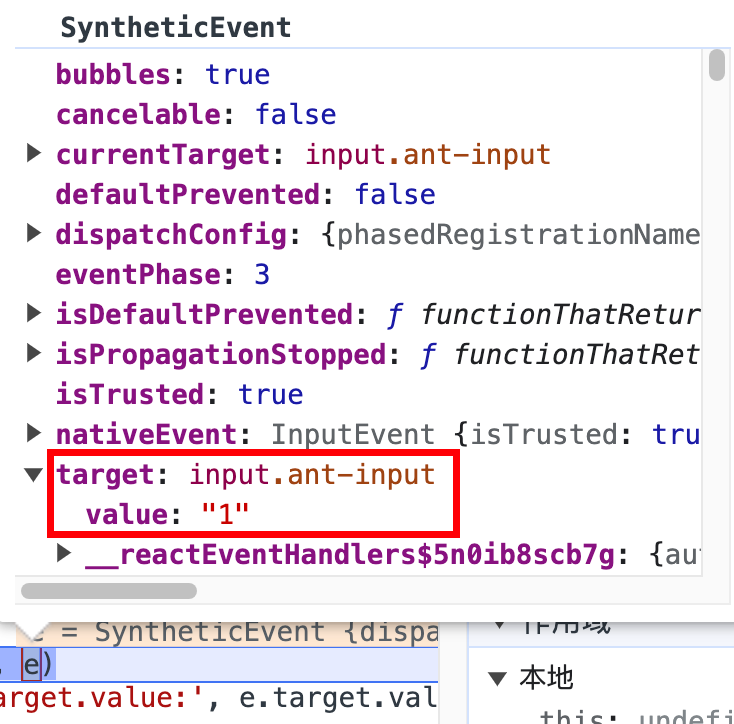
React16中打印事件对象取不到值的现象及其原因分析
React16中打印事件对象取不到值的现象及其原因分析 一、背景 在最近的开发过程中,遇到了一个看起来匪夷所思的问题❓: <Inputplaceholder"请输入"onChange{(e) > {console.log(e:, e)}}onKeyDown{handleKeyDown} />此时按理来说我…...

绝对干货-讲讲设计模式之创建型设计模式的本质
创建型模式(Creational Patterns):创建型模式关注对象的创建机制,包括了如何实例化一个对象或者一组对象的方法。Java中的创建型模式有:单例模式(Singleton Pattern)、工厂模式(简单…...
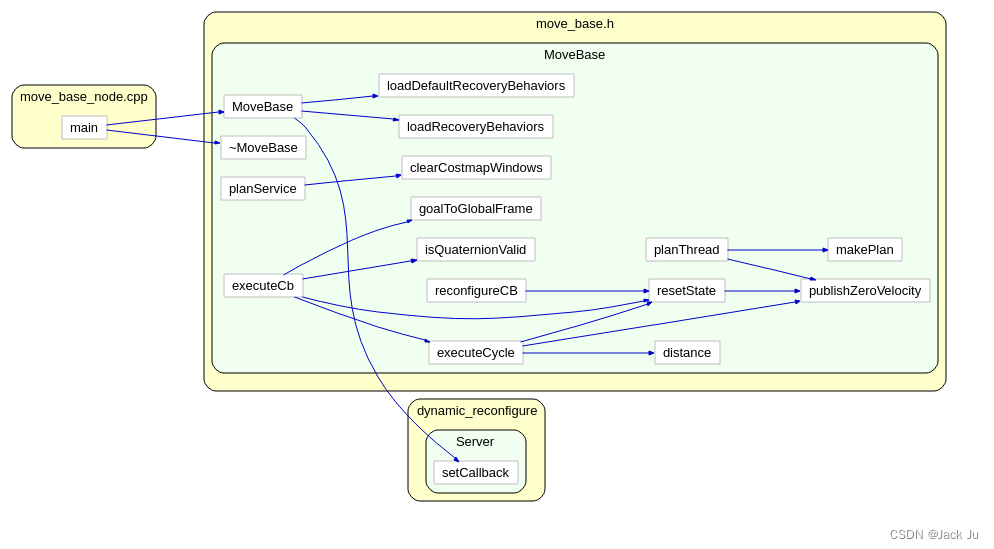
机器人规划算法——movebase导航框架源码分析
这里对MoveBase类的类成员进行了声明,以下为比较重要的几个类成员函数。 构造函数 MoveBase::MoveBase | 初始化Action 控制主体 MoveBase::executeCb收到目标,触发全局规划线程,循环执行局部规划 全局规划线程 void MoveBase::planThread |…...
)
Android:Google三方库之Firebase集成详细步骤(三)
Cloud Messaging 1、清单文件配置 a、(可选)一项扩展 FirebaseMessagingService 的服务。除了接收通知外,如果您还希望在后台应用中进行消息处理,则必须添加此服务。例如,您需要在前台应用中接收通知、接收数据载荷以及…...

2023年中国边缘计算网关现状及发展趋势分析[图]
边缘计算网关是一种可以在设备上运行本地计算、消息通信、数据缓存等功能的工业智能网关,可以在无需联网的情况下实现设备的本地联动以及数据处理分析。边缘计算网关是一种连接物联网设备和云端服务的关键技术,它可以在设备和云端之间建立一个安全、高效…...
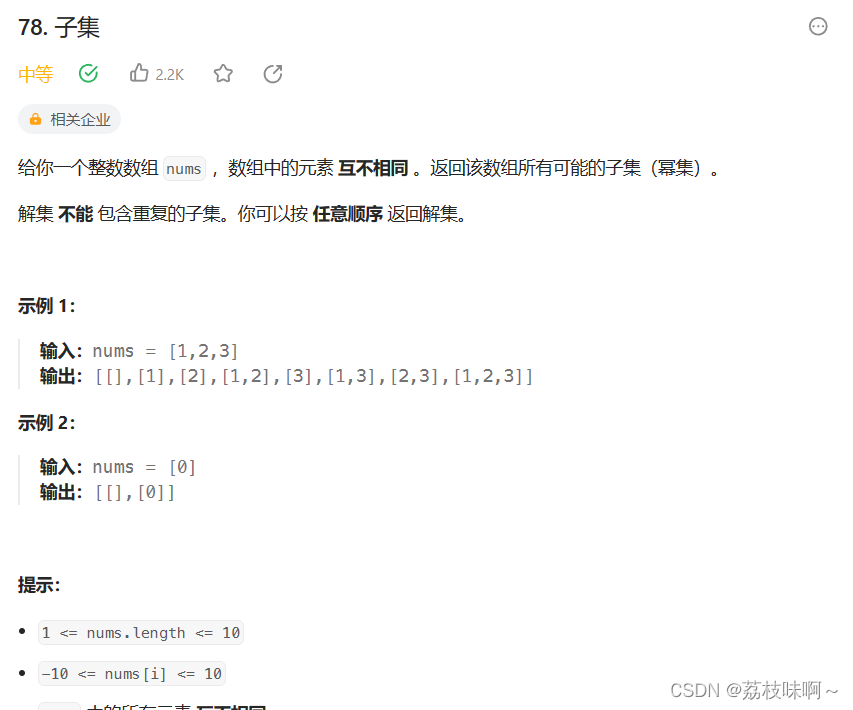
LeetCode78.子集
这道题如果用暴力法几乎是不可能解出来的,因为情况太复杂了,但是一旦用上递归回溯就会轻松很多,先上代码: class Solution {List<List<Integer>> result new ArrayList<List<Integer>>();List<Integ…...

不是默认进入Linux|总是自动进入windows系统
问题描述 不是默认进入Linux系统无法主动出现boot引导自动进入windows系统 尝试无效 修复引导无效重装Grub无效重装系统无效 环境 Ubuntu 22.04 LST微星主板 解决方案 修改引导顺序: 开机狂按Del键,进入BIOS系统,左侧Settings 设置&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
