蓝桥杯第四场双周赛(1~6)
1、水题
2、模拟题,写个函数即可
#define pb push_back
#define x first
#define y second
#define int long long
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f;
const LL llinf = 5e18;typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int a[N];
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
int qc(int a, int b , int c){return (a + b + c)/2;
}
int alg(int a , int b , int c){int cc = qc(a , b , c);return (cc * (cc - a) * (cc - b) * (cc - c));
}
void solve()
{int a , b , c;cin >> a >> b >> c;if(a + b <= c || a + c <= b || b + c <= a){cout << -1;}elsecout << alg(a , b , c);
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
// cin>>t;while(t--){solve();}return 0;
}
3、模拟题,找规律,第一行和最后一行只有两个数,其余行都是三个数。
第一行特殊处理,其余行: 就是当前所在行
,
就是所在行第s个数 , 每行第一个数是
, 因此所在列就是r - 1 + s。
#include <iostream>
using namespace std;
int main()
{long long n , m;cin >> n >> m;for(int i = 0 ; i < m ; i ++){long long x;cin >> x;if(x <= 1){cout << 1 << " " << x + 1 << endl;}else{long long r = (x + 1) / 3 + 1;long long st = x - ((r - 1) * 3 - 1);long long dc = r - 1 + st;cout << r << " " << dc << endl;}}return 0;
}4、![]() 考虑找到
考虑找到的所有可能取值,取值上界应该为
。由于
,因此每个肯定不超过64种取值。用三重循环找到所有
的所有取值,复杂度为
。注意
判断可能会爆long long , 所以在判断是否到达上界需要用
。用数组或者set去存每种取值,然后从小到大排序。按照题目条件对每个询问搜索即可(二分/暴力)。整体复杂度
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f;
const LL llinf = 2e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
LL a , b , c;
set<LL>st;
void solve()
{cin >> a >> b >> c;vector<LL>aa , bb , cc;aa.pb(1);bb.pb(1);cc.pb(1);LL x = 1;while(a != 1 && x < llinf / a){x *= a;aa.pb(x);}LL y = 1;while(b != 1 && y < llinf / b){y *= b;bb.pb(y);}LL z = 1;while(c != 1 && z < llinf / c){z *= c;cc.pb(z);}for(int i = 0 ; i < aa.size() ; i ++){for(int j = 0 ; j < bb.size() ; j ++){for(int z = 0 ; z < cc.size() ; z ++){st.insert(aa[i] + bb[j] + cc[z]);}}}int m;cin >> m;for(int i = 0 ; i < m ; i ++){LL que;cin >> que;auto it = st.upper_bound(que);while(*it - que == 1){que = *it;it = st.upper_bound(que);}cout << que + 1 << " " << (*it - que - 1) << endl;}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
// cin>>t;while(t--){solve();}return 0;
}
5、 方法很多,大体思路为将类型一样的宝石放到一起,将他们的作用区间进行合并,然后对整个数组进行区间修改。
区间合并:将所有区间按照左端点排序,遍历区间,若当前左端点与前一个区间右端点有重合部分,则将他们合并成一个区间,否则将前一个区间存下来,当前区间为一个新的区间。
区间修改:差分/树状数组/线段树。
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int a[N];
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
struct BIT{//Binary indexed Tree(树状数组)int n;vector<int> tr;BIT(int n) : n(n) , tr(n + 1 , 0){}int lowbit(int x){return x & -x;}void modify(int x , int modify_number){for(int i = x ; i <= n ; i += lowbit(i)){tr[i] += modify_number;}}void modify(int l , int r , int modify_number){modify(l , modify_number);modify(r + 1 , -modify_number);}int query(int x){int res = 0;for(int i = x ; i ; i -= lowbit(i))res += tr[i];return res;}int query(int x , int y){return query(y) - query(x);}
};
void solve()
{int n , m , q;cin >> n >> m >> q;vector<int>len(m + 5);for(int i = 1 ; i <= m ; i++){cin >> len[i];}BIT bit(n);vector<pair<int,int>>que;for(int i = 0 ; i < q ; i ++){int x , y;cin >> x >> y;que.pb({x , y});}sort(que.begin() , que.end());int r = 0 , pos = 0;for(int i = 0 ;i < q ; i ++){if(que[i].x != pos){pos = que[i].x;r = 0;}bit.modify( max(r + 1, que[i].y) , min(que[i].y + len[pos] - 1 , n) , 1);r = min(que[i].y + len[pos] - 1 , n);}for(int i = 1 ; i <= n ; i ++){cout << bit.query(i)<<" ";}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
// cin>>t;while(t--){solve();}return 0;
}6、删除区间求中位数比较困难。相反,增加数求区间中位数就是一道对顶堆的板子题了。因此考虑逆着做题,先将所有会飘走的气球放弃,将其余气球加入对顶堆。然后再从后往前依次添加气球,维护对顶堆找答案即可(对顶堆网上一大堆模板)。
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int a[N];
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;for(int i = 1 ; i <= n ; i ++){cin >> a[i];}cin >> m;double ans[m + 5];int que[m + 5];int vis[n + 5];memset(vis,0,sizeof vis);for(int i = 1 ; i <= m ; i ++){cin >> que[i];vis[que[i]] = 1;}for(int i = 1 ;i <= n ; i ++){if(!vis[i]){ma.push(a[i]);}}while(ma.size() > mi.size()){mi.push(ma.top());ma.pop();}for(int i = m ; i > 0 ; i --){if((mi.size() + ma.size()) % 2 == 0){//偶数int x = mi.top();int y = ma.top();ans[i] = (double)(1.0 * x + y) / 2;}else{double x = mi.top();ans[i] = (double)(1.0 * x);}int yy = mi.top();if(a[que[i]] > yy){mi.push(a[que[i]]);}else{ma.push(a[que[i]]);}while(mi.size() > ma.size() + 1){ma.push(mi.top());mi.pop();}while(ma.size() > mi.size()){mi.push(ma.top());ma.pop();}}for(int i = 1 ; i <= m ; i++){printf("%.1f " , ans[i]);}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
// cin>>t;while(t--){solve();}return 0;
}
7、边数据较小,网络流问题。
相关文章:
蓝桥杯第四场双周赛(1~6)
1、水题 2、模拟题,写个函数即可 #define pb push_back #define x first #define y second #define int long long #define endl \n const LL maxn 4e057; const LL N 5e0510; const LL mod 1e097; const int inf 0x3f3f; const LL llinf 5e18;typedef pair…...

【Web】CmsEasy 漏洞复现
访问主页 到处点一点没啥发现 扫目录 访问/admin 账号密码都是admin admin(弱口令) 登录成功 看到左边列表有模板,心里大概有数了哈 进行一波历史漏洞的查 CmsEasy_v5.7 漏洞测试 payload1: 1111111111";}<?php phpinfo()?> payload2: 11";…...
Spring 中存储 Bean 的相关注解
Bean的存 IoC控制反转,就是将对象的控制权交给Spring的IOC容器,由IOC容器创建及管理对象。 也就是bean的存储 类注解:五大注解 Controller(控制器存储) Service(服务存储) Component(组件存储…...

Proteus下仿真AT89C51单片机串行口的问题
在Proteus下仿真AT89C51单片机的串行口的时候,Proteu不同版本下差别较大。 同样的程序,在7.8的老版本(7.8版本的原理图仿真软件名称是ISIS 7 Professional)下仿真串行口,收发均正常。但是,在8.13版…...

java学习part17
110-面向对象(高级)-关键字final的使用及真题_哔哩哔哩_bilibili 1.概念 tips:java里有const关键字,但是用于保留字,不会使用,目前没有意义。 final变量没有默认赋值,只能在以下三个地方赋值,且只能赋值一…...

Centos 7、Debian、Ubuntu中tree指令的检查与下载
目录 前言 Centos 7中检查tree指令是否安装的两种办法 which指令检查 查看当前版本指令 不同版本下安装tree指令 Centos 7的发行版本 重点 Debian的发行版本 重点 Ubuntu的发行版本 重点 前言 在大多数Linux发行版中,tree命令通常不是默认安装的指令。…...

深拷贝函数
<script>//深拷贝:// 对于基本数据类型来说,拷贝的是栈// 对于复杂数据类型也就是对象来说,拷贝的是堆。深拷贝后引用地址是不同的function deepClone(val){// val是数组if(Array.isArray(val)){let cloneArr []for(let i 0;i < v…...

python小数据分析小结及算法实践集锦
在缺乏大量历史数据的新兴技术和产业中,商业分析可能会面临一些挑战。然而,有一些技术和方法可以帮助分析者在数据不充分的情况下进行科学化商业分析,并为决策提供支持。 1. 当面对缺乏大量历史数据的新兴技术和产业时所采常用的技术和方法 …...

【docker系列】docker高阶篇
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
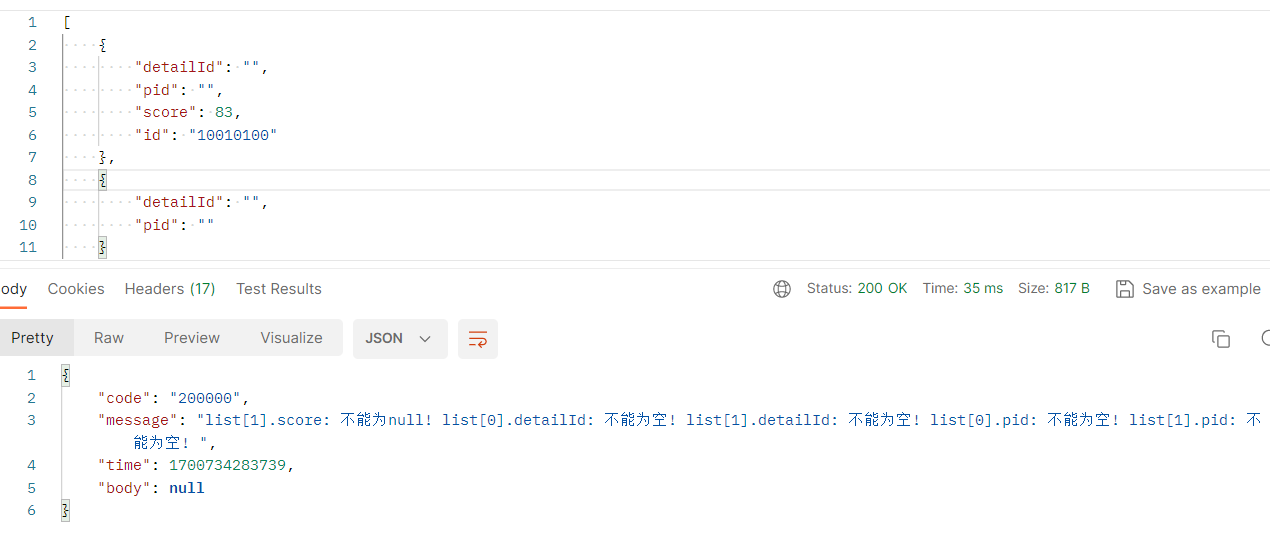
SpringBoot校验List失效解决方法
文章目录 SpringBoot校验List失效解决方法附:校验基本数据类型和String类型的方法参数时也需要在类上加Validated SpringBoot校验List失效解决方法 失效场景示例代码: RestController RequestMapping("/v1/jx/flowSummary") Slf4j public cl…...
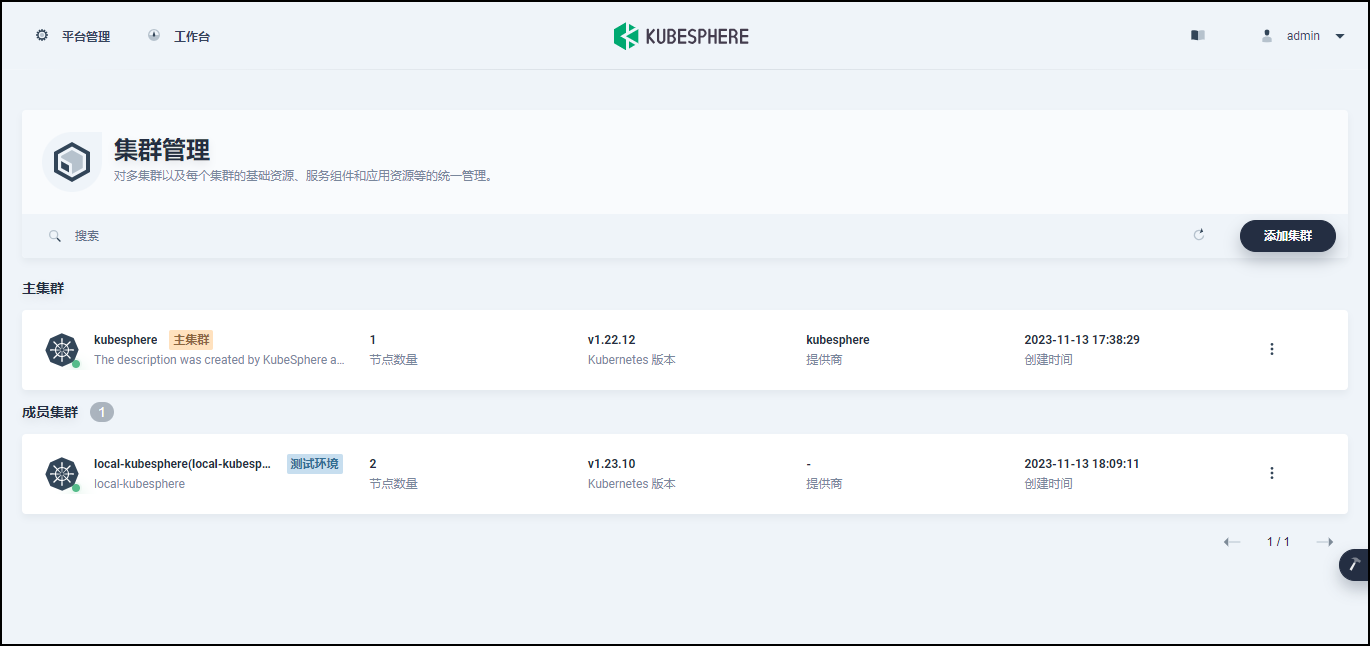
【KubeSphere】基于AWS在 Linux 上以 All-in-One 模式安装 KubeSphere
文章目录 一、实验配置说明二、实验准备工作1.确认系统版本2. 修改网络DNS3. 关闭SELINUX4. 关闭防火墙 三、实验依赖项安装四、下载 KubeKey五、一键化安装部署六、验证安装结果七、登录KubeSphere管理控制台八、参考链接 一、实验配置说明 本实验基于AWS启动一台新实例&…...
数)
3.一维数组——输入十个数,输出其中最大(小)数
文章目录 前言一、题目描述 二、题目分析 三、解题 程序运行代码 前言 本系列为一维数组编程题,点滴成长,一起逆袭。 一、题目描述 输入十个数,输出其中最大(小)数 二、题目分析 打擂台法:maxa[0]; 最大…...
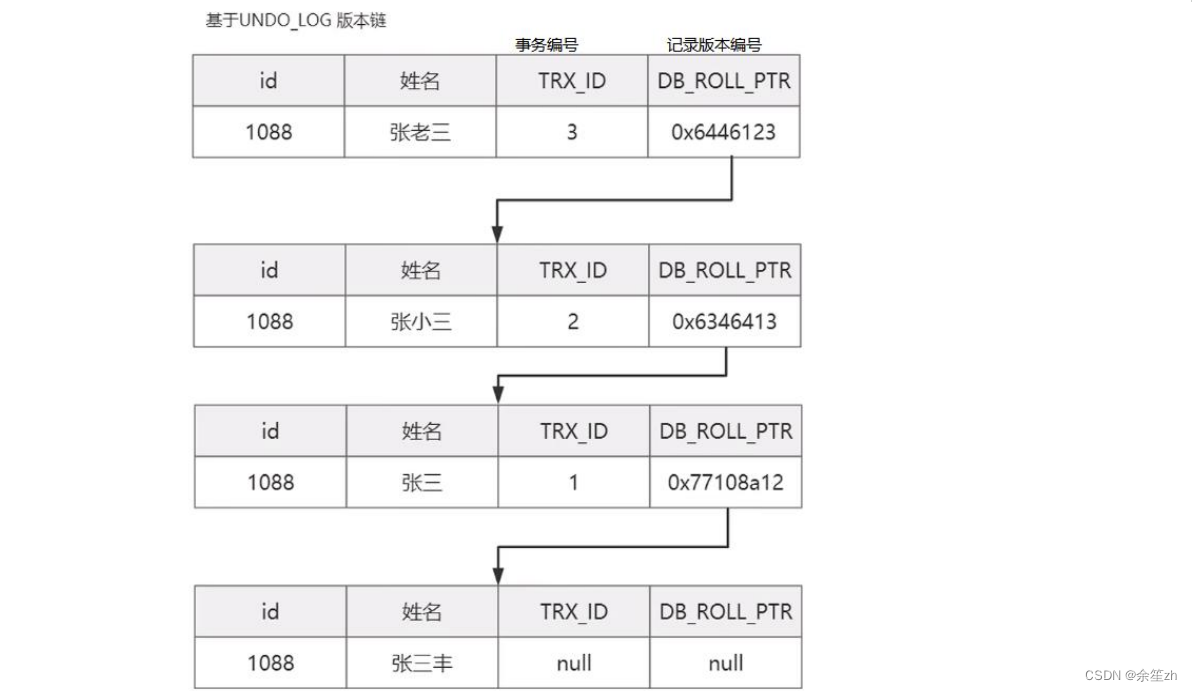
mysql高级知识点
一、mysql架构 连接层:负责接收客户端的连接请求,可以进行授权、认证(验证账号密码)。服务层:负责调用sql接口,对sql语法进行解析,对查询进行优化,缓存。引擎层:是真正进行执行sql的地方&#x…...
python pdf转txt文本、pdf转json
文章目录 一、前言二、实现方法1. 目录结构2. 代码 一、前言 此方法只能转文本格式的pdf,如果是图片格式的pdf需要用到ocr包,以后如果有这方面需求再加这个方法 二、实现方法 1. 目录结构 2. 代码 pdf2txt.py 代码如下 #!/usr/bin/env python # -*- …...

LabVIEW中如何达到NI SMU最大采样率
LabVIEW中如何达到NI SMU最大采样率 NISMU的数字化仪功能对于捕获SMU详细的瞬态响应特性或表征待测设备(DUT)响应(例如线性调整率和负载调整率)至关重要。没有此功能,将需要一个外部示波器。 例如,假设在…...

redis运维(二十)redis 的扩展应用 lua(二)
一 redis 的扩展应用 lua redis lua脚本语法 ① 什么是脚本缓存 redis 缓存lua脚本 说明: 重启redis,脚本缓存会丢失 下面讲解 SCRIPT ... 系列 SCRIPT ② LOAD 语法:SCRIPT LOAD lua代码 -->载入一个脚本,只是预加载,不执行思考1࿱…...

Docker ps命令
docker ps:列出容器。 语法: docker ps [OPTIONS]OPTIONS说明: -a:显示所有的容器,包括未运行的。 -f:根据条件过滤显示的内容。 --format:指定返回值的模板文件。 -l:显示最近…...

前端实现留言板
留言板的主要使用场景是为用户提供一个在网站或应用上留言的平台,这样他们可以分享自己的想法、意见或建议。这些留言可以帮助开发者收集用户反馈,从而改进产品或服务。 使用HTML、CSS和JavaScript实现的留言板:这种方法的优点是简单易实现&a…...
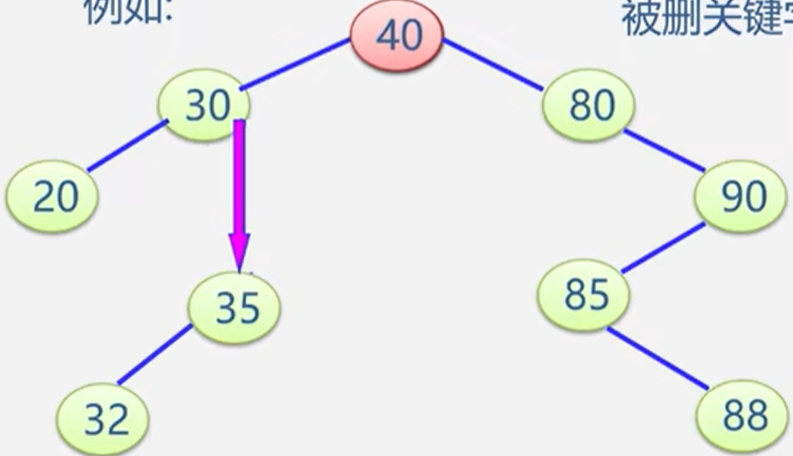
【二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)二叉排序树的操作----插入生成删除】
文章目录 二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)二叉树的查找分析二叉排序树的操作----插入二叉排序树的操作----生成二叉排序树的操作----删除 二叉排序树(Binary Sort Tree…...

Verilog基础:时序调度中的竞争(二)
相关阅读 Verilog基础https://blog.csdn.net/weixin_45791458/category_12263729.html?spm1001.2014.3001.5482 作为一个硬件描述语言,Verilog HDL常常需要使用语句描述并行执行的电路,但其实在仿真器的底层,这些并行执行的语句是有先后顺序…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
