Pytorch深度学习实战2-1:详细推导Xavier参数初始化(附Python实现)
目录
- 1 参数初始化
- 2 Xavier参数初始化原理
- 2.1 前向传播阶段
- 2.2 反向传播阶段
- 2.3 可视化思考
- 3 Python实现
1 参数初始化
参数初始化在深度学习中起着重要的作用。在神经网络中,参数初始化是指为模型中的权重和偏置项设置初始值的过程。合适的参数初始化可以帮助模型更好地学习和收敛到最优解。参数初始化的目标是使模型具有良好的初始状态,以便在训练过程中快速且稳定地收敛。错误的参数初始化可能导致模型无法正常学习,梯度消失或梯度爆炸等问题。
常见的参数初始化方法包括随机初始化、零初始化、正态分布初始化和均匀分布初始化等。这些方法根据不同的分布特性和模型结构选择合适的初始值。在某些情况下,不同层或不同类型的参数可能需要不同的初始化策略。例如使用预训练模型时,可以采用迁移学习的方法,将预训练模型的参数作为初始值,从而加速收敛并提高性能。
除了设置初始值外,参数初始化还可以与其他优化技术相结合,如学习率调整、正则化和批归一化等,以进一步提高模型的性能和稳定性
举例而言,如图所示是在 t a n h ( ⋅ ) \rm{tanh(\cdot)} tanh(⋅)下九层神经网络各层激活输出,可以看到在网络深层激活输出逐渐衰减或保持不变

2 Xavier参数初始化原理
Xavier初始化的核心原理是保证各层网络的前向传播激活值和反向传播梯度值方差保持一致。Xavier初始化基于如下假设:
- 输入样本独立同分布采样,且各个特征维度方差相等;
- 激活函数 σ ( ⋅ ) \sigma \left( \cdot \right) σ(⋅)对称且近似线性区间满足 σ ( z ) ≈ z ⇔ σ ′ ( z ) ≈ 1 \sigma \left( \boldsymbol{z} \right) \approx \boldsymbol{z}\Leftrightarrow \sigma '\left( \boldsymbol{z} \right) \approx 1 σ(z)≈z⇔σ′(z)≈1;
- 激活输入 z \boldsymbol{z} z处于激活函数的线性区间
2.1 前向传播阶段
根据
a l = σ ( z l ) = σ ( W l a l − 1 − b l ) \boldsymbol{a}^l=\sigma \left( \boldsymbol{z}^l \right) =\sigma \left( \boldsymbol{W}^l\boldsymbol{a}^{l-1}-\boldsymbol{b}^l \right) al=σ(zl)=σ(Wlal−1−bl)
可得
v a r [ a l ] ≈ v a r [ z l ] = v a r [ W l a l − 1 − b l ] \mathrm{var}\left[ \boldsymbol{a}^l \right] \approx \mathrm{var}\left[ \boldsymbol{z}^l \right] =\mathrm{var}\left[ \boldsymbol{W}^l\boldsymbol{a}^{l-1}-\boldsymbol{b}^l \right] var[al]≈var[zl]=var[Wlal−1−bl]
初始阶段第 l l l层的网络权重 W l \boldsymbol{W}^l Wl的各个元素独立采样自某个分布 P P P,即
[ z 1 l z 2 l ⋮ z n l l ] = [ w 1 , 1 l w 1 , 2 l ⋯ w 1 , n l − 1 l w 2 , 1 l w 2 , 2 l ⋯ w 2 , n l − 1 l ⋮ ⋮ ⋱ ⋮ w n l , 1 l w n l , 2 l ⋯ w n l , n l − 1 l ] [ a 1 l − 1 a 2 l − 1 ⋮ a n l − 1 l − 1 ] ⇒ v a r [ z i l ] = v a r [ ∑ k = 1 n l − 1 w 1 , k l a k l − 1 ] \left[ \begin{array}{c} z_{1}^{l}\\ z_{2}^{l}\\ \vdots\\ z_{n_l}^{l}\\\end{array} \right] =\left[ \begin{matrix} w_{1,1}^{l}& w_{1,2}^{l}& \cdots& w_{1,n_{l-1}}^{l}\\ w_{2,1}^{l}& w_{2,2}^{l}& \cdots& w_{2,n_{l-1}}^{l}\\ \vdots& \vdots& \ddots& \vdots\\ w_{n_l,1}^{l}& w_{n_l,2}^{l}& \cdots& w_{n_l,n_{l-1}}^{l}\\\end{matrix} \right] \left[ \begin{array}{c} a_{1}^{l-1}\\ a_{2}^{l-1}\\ \vdots\\ a_{n_{l-1}}^{l-1}\\\end{array} \right] \Rightarrow \mathrm{var}\left[ z_{i}^{l} \right] =\mathrm{var}\left[ \sum_{k=1}^{n_{l-1}}{w_{1,k}^{l}a_{k}^{l-1}} \right] z1lz2l⋮znll = w1,1lw2,1l⋮wnl,1lw1,2lw2,2l⋮wnl,2l⋯⋯⋱⋯w1,nl−1lw2,nl−1l⋮wnl,nl−1l a1l−1a2l−1⋮anl−1l−1 ⇒var[zil]=var[k=1∑nl−1w1,klakl−1]
考虑到 w i , j l w_{i,j}^{l} wi,jl与前一层激活值 a l − 1 \boldsymbol{a}^{l-1} al−1独立,所以
v a r [ z i l ] = v a r [ ∑ k = 1 n l − 1 w i , k l a k l − 1 ] = ∑ k = 1 n l − 1 v a r [ w i , k l a k l − 1 ] = ∑ k = 1 n l − 1 ( v a r [ w i , k l ] v a r [ a k l − 1 ] + v a r [ w i , k l ] E 2 [ a k l − 1 ] + v a r [ a k l − 1 ] E 2 [ w i , k l ] ) \begin{aligned}\mathrm{var}\left[ z_{i}^{l} \right] &=\mathrm{var}\left[ \sum_{k=1}^{n_{l-1}}{w_{i,k}^{l}a_{k}^{l-1}} \right]\\& =\sum_{k=1}^{n_{l-1}}{\mathrm{var}\left[ w_{i,k}^{l}a_{k}^{l-1} \right]}\\&=\sum_{k=1}^{n_{l-1}}{\left( \mathrm{var}\left[ w_{i,k}^{l} \right] \mathrm{var}\left[ a_{k}^{l-1} \right] +\mathrm{var}\left[ w_{i,k}^{l} \right] \mathbb{E} ^2\left[ a_{k}^{l-1} \right] +\mathrm{var}\left[ a_{k}^{l-1} \right] \mathbb{E} ^2\left[ w_{i,k}^{l} \right] \right)}\end{aligned} var[zil]=var[k=1∑nl−1wi,klakl−1]=k=1∑nl−1var[wi,klakl−1]=k=1∑nl−1(var[wi,kl]var[akl−1]+var[wi,kl]E2[akl−1]+var[akl−1]E2[wi,kl])
根据激活函数对称性,可令 W l \boldsymbol{W}^l Wl、 a l − 1 \boldsymbol{a}^{l-1} al−1均值为0,根据假设中的方差关系
{ ∀ i v a r [ a i l ] = v a r [ a l ] ∀ i , j v a r [ w i , j l ] = v a r [ W l ] \begin{cases} \forall i\,\,\mathrm{var}\left[ a_{i}^{l} \right] =\mathrm{var}\left[ \boldsymbol{a}^l \right]\\ \forall i,j\,\,\mathrm{var}\left[ w_{i,j}^{l} \right] =\mathrm{var}\left[ \boldsymbol{W}^l \right]\\\end{cases} {∀ivar[ail]=var[al]∀i,jvar[wi,jl]=var[Wl]
上式可简化为 v a r [ z i l ] = n l − 1 v a r [ w i , 1 l ] v a r [ a 1 l − 1 ] \mathrm{var}\left[ z_{i}^{l} \right] =n_{l-1}\mathrm{var}\left[ w_{i,1}^{l} \right] \mathrm{var}\left[ a_{1}^{l-1} \right] var[zil]=nl−1var[wi,1l]var[a1l−1],改写成矩阵形式
v a r [ a l ] ≈ n l − 1 v a r [ W l ] v a r [ a l − 1 ] \mathrm{var}\left[ \boldsymbol{a}^l \right] \approx n_{l-1}\mathrm{var}\left[ \boldsymbol{W}^l \right] \mathrm{var}\left[ \boldsymbol{a}^{l-1} \right] var[al]≈nl−1var[Wl]var[al−1]
结合 a 0 = x \boldsymbol{a}^0=\boldsymbol{x} a0=x可递推得到
v a r [ a l ] ≈ v a r [ x ] ∏ k = 1 l n k − 1 v a r [ W k ] {\mathrm{var}\left[ \boldsymbol{a}^l \right] \approx \mathrm{var}\left[ \boldsymbol{x} \right] \prod_{k=1}^l{n_{k-1}\mathrm{var}\left[ \boldsymbol{W}^k \right]}} var[al]≈var[x]k=1∏lnk−1var[Wk]
2.2 反向传播阶段
根据 δ l = ( W l + 1 ) T δ l + 1 ⊙ σ ′ ( z l ) \boldsymbol{\delta }^l=\left( \boldsymbol{W}^{l+1} \right) ^T\boldsymbol{\delta }^{l+1}\odot \sigma '\left( \boldsymbol{z}^l \right) δl=(Wl+1)Tδl+1⊙σ′(zl)可得
v a r [ δ l ] ≈ n l + 1 v a r [ W l + 1 ] v a r [ δ l + 1 ] \mathrm{var}\left[ \boldsymbol{\delta }^l \right] \approx n_{l+1}\mathrm{var}\left[ \boldsymbol{W}^{l+1} \right] \mathrm{var}\left[ \boldsymbol{\delta }^{l+1} \right] var[δl]≈nl+1var[Wl+1]var[δl+1]
结合 δ L = ∇ y ~ E ⊙ σ ′ ( z L ) ≈ ∇ y ~ E \boldsymbol{\delta }^L=\nabla _{\boldsymbol{\tilde{y}}}E\odot \sigma '\left( \boldsymbol{z}^L \right) \approx \nabla _{\boldsymbol{\tilde{y}}}E δL=∇y~E⊙σ′(zL)≈∇y~E可递推得到
v a r [ δ l ] ≈ ∇ y ~ E ∏ k = l + 1 L n k v a r [ W k ] {\mathrm{var}\left[ \boldsymbol{\delta }^l \right] \approx \nabla _{\boldsymbol{\tilde{y}}}E\prod_{k=l+1}^L{n_k\mathrm{var}\left[ \boldsymbol{W}^k \right]}} var[δl]≈∇y~Ek=l+1∏Lnkvar[Wk]
为保证前向传播激活和反向传播梯度在网络中顺利流动,应保持各层参数方差相等,即满足
{ n l v a r [ W l ] = 1 n l − 1 v a r [ W l ] = 1 \begin{cases} n_l\mathrm{var}\left[ \boldsymbol{W}^l \right] =1\\ n_{l-1}\mathrm{var}\left[ \boldsymbol{W}^l \right] =1\\\end{cases} ⎩ ⎨ ⎧nlvar[Wl]=1nl−1var[Wl]=1
由于第 l l l层的输入神经元个数 n l − 1 n_{l-1} nl−1和输出神经元个数 n l n_l nl一般不相等,故取折中
v a r [ W l ] = 2 n l − 1 + n l \mathrm{var}\left[ \boldsymbol{W}^l \right] =\frac{2}{n_{l-1}+n_l} var[Wl]=nl−1+nl2
所以网络连接权采样自服从方差满足上式的分布即可,例如
W ∼ N ( 0 , 2 n l − 1 + n l ) o r W ∼ U ( − 6 n l − 1 + n l , 6 n l − 1 + n l ) \boldsymbol{W}\sim \mathcal{N} \left( 0,\frac{2}{n_{l-1}+n_l} \right) \,\, \mathrm{or} \boldsymbol{W}\sim U\left( -\sqrt{\frac{6}{n_{l-1}+n_l}},\sqrt{\frac{6}{n_{l-1}+n_l}} \right) W∼N(0,nl−1+nl2)orW∼U(−nl−1+nl6,nl−1+nl6)
2.3 可视化思考
如图所示,经过Xavier初始化后网络各层前向和反向传播时的方差保持一致

如图所示,经过Xavier初始化后的测试误差通常更小

Xavier进一步指出:观察层与层之间传播的激活值和梯度有利于理解深层网络的训练复杂度;保持层与层之间激活值和梯度的良好流动对学习效果非常重要。尽管在Xavier初始化做出了比较苛刻的假设,且在工程上很容易被违反,但其在实践中被证明是有效的,已经成为很多深度学习框架的默认初始化方法之一。
3 Python实现
简单实现一下Xavier初始化
def initialize_parameters_xavier(layers_dims):parameters = {}L = len(layers_dims)for l in range(1, L):mu = 0sigma = np.sqrt(2.0 / (layers_dims[l - 1] + layers_dims[l]))parameters['W' + str(l)] = np.random.normal(loc=mu, scale=sigma, size=(layers_dims[l], layers_dims[l - 1]))parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))return parameters
可视化
for l in range(1, num_layers):A_pre = AW = parameters['W' + str(l)]b = parameters['b' + str(l)]z = np.dot(W, A_pre) + b # z = Wx + bA = tanh(z)print(A)plt.subplot(1, 8, l)plt.hist(A.flatten(), facecolor='g')plt.xlim([-2, 2])plt.ylim([0, 1000000])plt.yticks([])
plt.show()
如下所示

可以看出各层输出方差基本一致,实现了良好的初始化效果
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

Pytorch深度学习实战2-1:详细推导Xavier参数初始化(附Python实现)
目录 1 参数初始化2 Xavier参数初始化原理2.1 前向传播阶段2.2 反向传播阶段2.3 可视化思考 3 Python实现 1 参数初始化 参数初始化在深度学习中起着重要的作用。在神经网络中,参数初始化是指为模型中的权重和偏置项设置初始值的过程。合适的参数初始化可以帮助模型…...

Java的threadd常用方法
常用API 给当前线程命名 主线程 package com.itheima.d2;public class ThreadTest1 {public static void main(String[] args) {Thread t1 new MyThread("子线程1");//t1.setName("子线程1");t1.start();System.out.println(t1.getName());//获得子线程…...
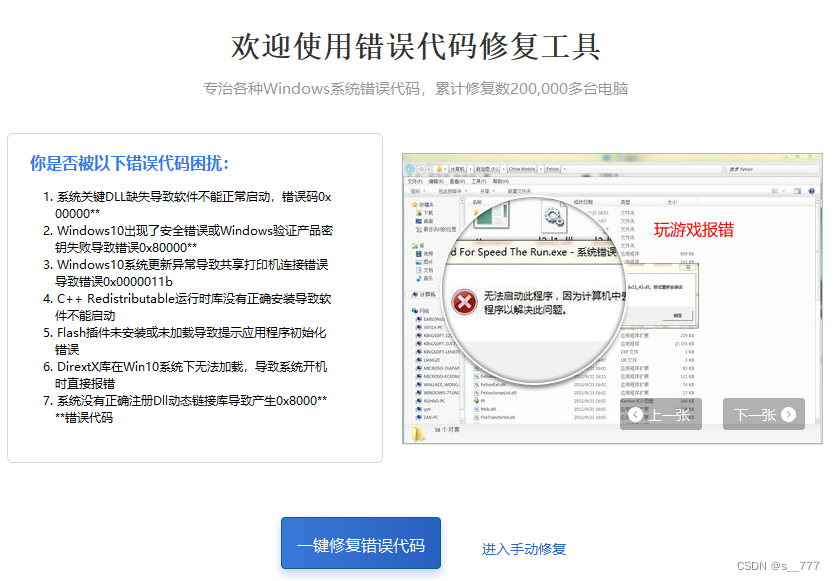
一键修复0xc000007b错误代码,科普关于0xc000007b错误的原因
最近很多用户都有遇到过0xc000007b错误的问题,出现这样的问题想必大家都会手足无措吧,其实解决这样的问题也有很简单的解决方法,这篇文章就来教大家如何一键修复0xc000007b,同时给大家科普一下关于0xc000007b错误的原因࿰…...
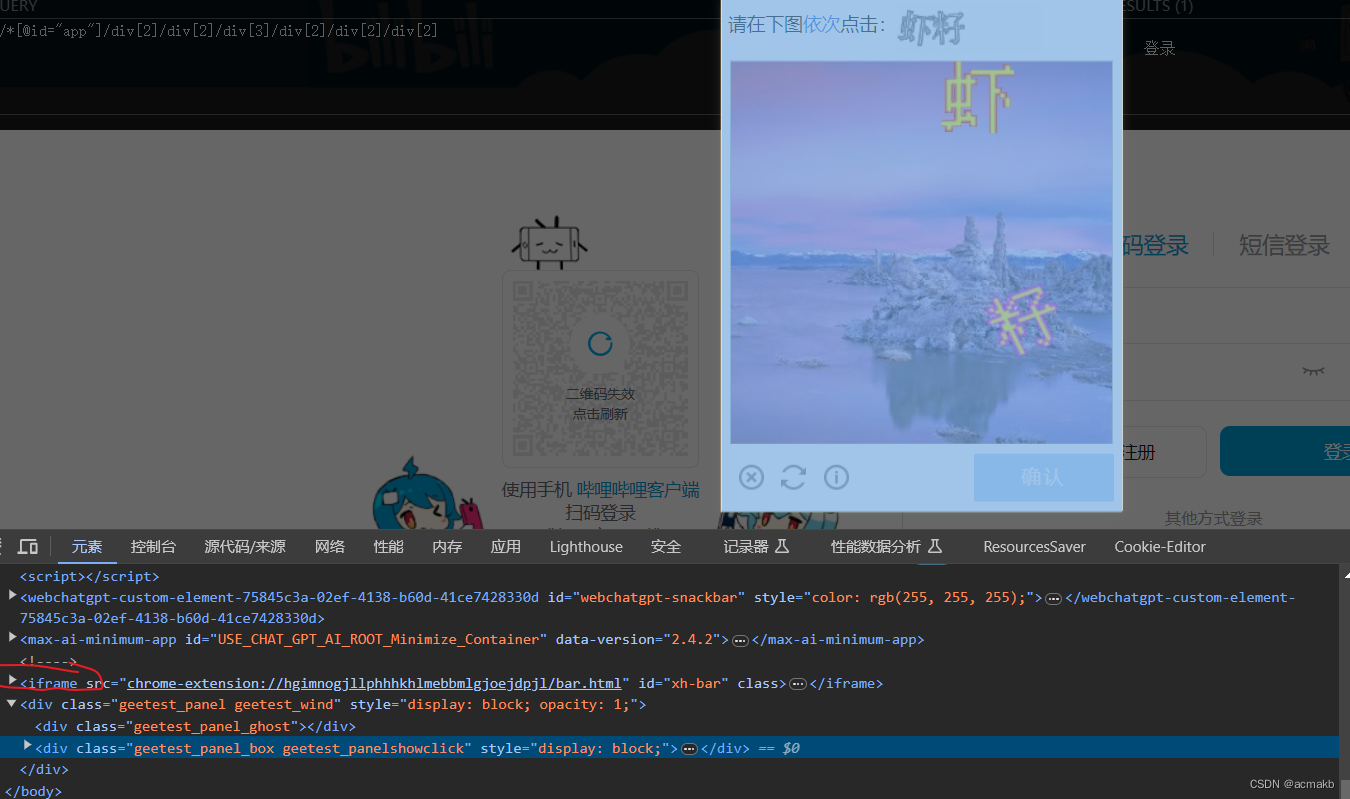
使用Selenium、Python和图鉴打码平台实现B站登录
selenium实战之模拟登录b站 基础知识铺垫: 利用selenium进行截图: driver.save_screenshot() 注意图片文件名要用png结尾. 关于移动: ActionChains(bro).move_to_element_with_offset()# 对于某个图像ActionChains(bro).move_by_offset(…...

嵌入式设备视频编码比较:H.264、H.265、MPEG-2和MJPG
在嵌入式设备领域,视频编码是一项关键技术,它能够将高清视频压缩为更小的数据量,以实现高效的存储和传输。本文将对四种常见的视频编码标准进行详细比较,包括H.264(AVC)、H.265(HEVC)…...

创意二维码案例:意大利艺术家的最新二维码艺术展!
意大利艺术家——米开朗基罗皮斯特莱托(Michelangelo Pistoletto)的个人艺术展“二维码‘说’”(QR CODE POSSESSION)正在北京798艺术区的常青艺术画廊展出,这是一次别出心裁的创意艺术展! 主要体现在3个方…...
XML映射文件
<?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapperPUBLIC "-//mybatis.org//DTD Mapper 3.0//EN""http://mybatis.org/dtd/mybatis-3-mapper.dtd"> <mapper namespace"org.mybatis.example.BlogMapper&q…...
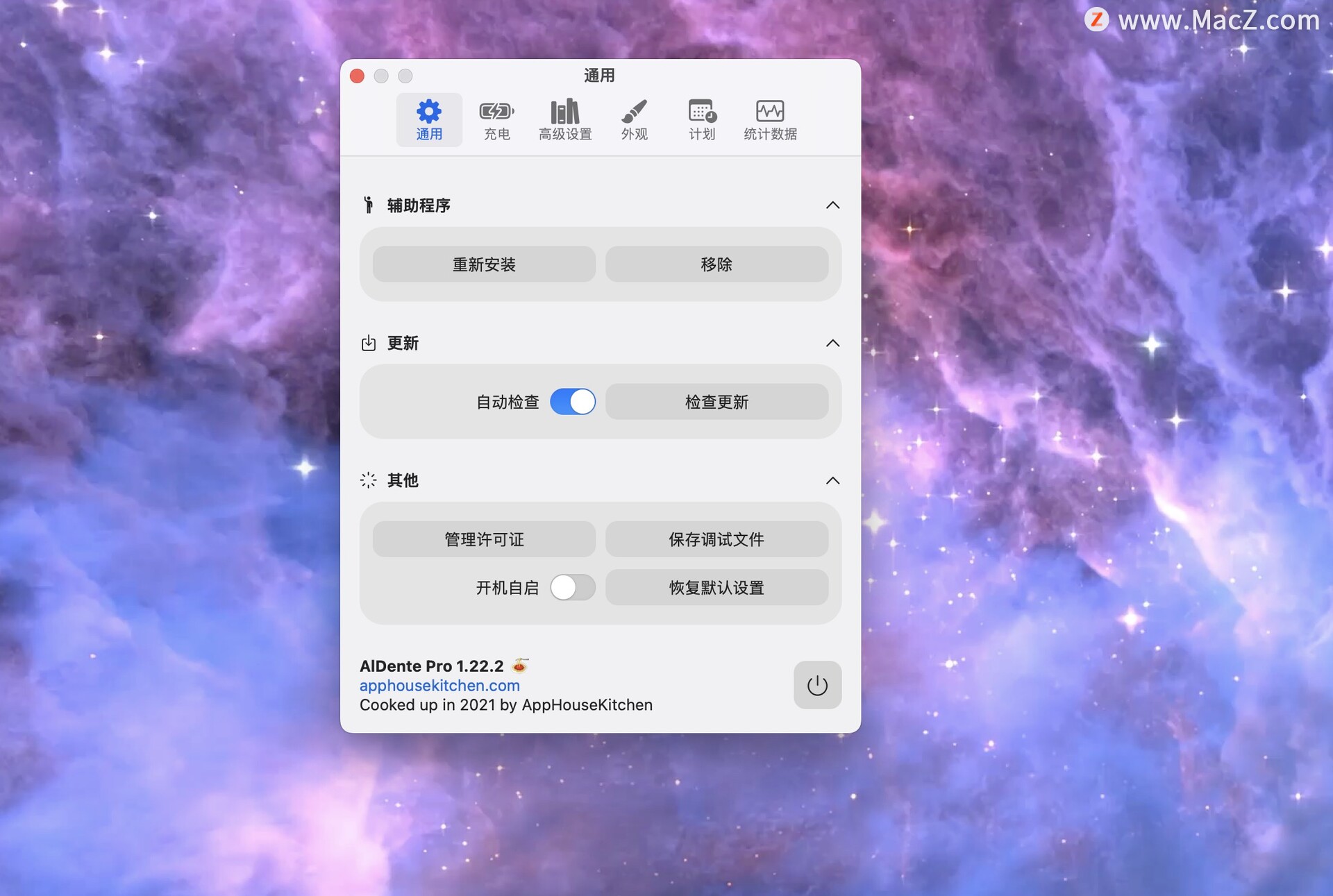
AlDente Pro v1.22.2(mac电池最大充电限制工具)
AlDente Pro是一款适用于Mac操作系统的小工具,可以帮助您限制电池充电量以延长电池寿命。通常情况下,电池在充满的状态下会继续接受电源充电,这可能会导致电池寿命缩短。使用AlDente Pro,您可以设置电池只充到特定的充电水平&…...
原生小程序图表
原生小程序使用图表 话不多说直接进入正题 官方文档: https://www.ucharts.cn/v2/#/ 下载文件 首先去gitee上把文件下载到自己的项目中 https://gitee.com/uCharts/uCharts 找到微信小程序和里面的组件 把里面src下的文件全部下载下来放入自己项目中 项目文件 新建文件…...

UniPro集成华为云WeLink 为企业客户构建互为联接的协作平台
华为云WeLink是华为开启数字化办公体验、帮助企业实现数字化转型的实践,类似钉钉。UniPro的客户企业中,有使用WeLink作为协作工具的,基于客户的实际业务需求,UniPro实现了与WeLink集成的能力,以帮助客户企业丰富和扩展…...

【论文解读】基于生成式面部先验的真实世界盲脸修复
论文地址:https://arxiv.org/pdf/2101.04061.pdf 代码地址:https://github.com/TencentARC/GFPGAN 图片解释: 与最先进的面部修复方法的比较:HiFaceGAN [67]、DFDNet [44]、Wan 等人。[61] 和 PULSE [52] 在真实世界的低质量图像…...
蓝桥杯第四场双周赛(1~6)
1、水题 2、模拟题,写个函数即可 #define pb push_back #define x first #define y second #define int long long #define endl \n const LL maxn 4e057; const LL N 5e0510; const LL mod 1e097; const int inf 0x3f3f; const LL llinf 5e18;typedef pair…...

【Web】CmsEasy 漏洞复现
访问主页 到处点一点没啥发现 扫目录 访问/admin 账号密码都是admin admin(弱口令) 登录成功 看到左边列表有模板,心里大概有数了哈 进行一波历史漏洞的查 CmsEasy_v5.7 漏洞测试 payload1: 1111111111";}<?php phpinfo()?> payload2: 11";…...
Spring 中存储 Bean 的相关注解
Bean的存 IoC控制反转,就是将对象的控制权交给Spring的IOC容器,由IOC容器创建及管理对象。 也就是bean的存储 类注解:五大注解 Controller(控制器存储) Service(服务存储) Component(组件存储…...

Proteus下仿真AT89C51单片机串行口的问题
在Proteus下仿真AT89C51单片机的串行口的时候,Proteu不同版本下差别较大。 同样的程序,在7.8的老版本(7.8版本的原理图仿真软件名称是ISIS 7 Professional)下仿真串行口,收发均正常。但是,在8.13版…...

java学习part17
110-面向对象(高级)-关键字final的使用及真题_哔哩哔哩_bilibili 1.概念 tips:java里有const关键字,但是用于保留字,不会使用,目前没有意义。 final变量没有默认赋值,只能在以下三个地方赋值,且只能赋值一…...

Centos 7、Debian、Ubuntu中tree指令的检查与下载
目录 前言 Centos 7中检查tree指令是否安装的两种办法 which指令检查 查看当前版本指令 不同版本下安装tree指令 Centos 7的发行版本 重点 Debian的发行版本 重点 Ubuntu的发行版本 重点 前言 在大多数Linux发行版中,tree命令通常不是默认安装的指令。…...

深拷贝函数
<script>//深拷贝:// 对于基本数据类型来说,拷贝的是栈// 对于复杂数据类型也就是对象来说,拷贝的是堆。深拷贝后引用地址是不同的function deepClone(val){// val是数组if(Array.isArray(val)){let cloneArr []for(let i 0;i < v…...

python小数据分析小结及算法实践集锦
在缺乏大量历史数据的新兴技术和产业中,商业分析可能会面临一些挑战。然而,有一些技术和方法可以帮助分析者在数据不充分的情况下进行科学化商业分析,并为决策提供支持。 1. 当面对缺乏大量历史数据的新兴技术和产业时所采常用的技术和方法 …...

【docker系列】docker高阶篇
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
